Модель конкуренции наукоемких производственных комплексов при разработке инновационной продукции

По данным Росстата по итогам 2020 года объем ВВП России сократился на 3,1% в годовом выражении. Номинальный объем ВВП в 2020 году составил 106,6 трлн руб. [1]. Для сравнения, падение ВВП США в 2020 году составило 3,5%, Германии - 5%, Франции - 8,3%. В современном развитии экономики и общества все большее значение приобретает генерация новых знаний и распространение нововведений. Мировой и отечественный опыт свидетельствует о том, что в конкурентной борьбе крупных корпораций идет соперничество не только за обладание капитальными ресурсами и материальными ценностями, но и за лидерство в разработке и внедрении инноваций. Экономический рост наукоемких отраслей все в большей степени определяется той долей объема продукции и прибыли, которые получены за счет инноваций [2, 3]. Для исследования особенностей, основных тенденций и темпов развития наукоемких производственных комплексов (НПК), анализа научно-технического и социальноэкономического прогресса, изучения и внедрения инноваций в условиях трансформации отечественной экономики представляется целесообразным разработать модель конкуренции в области научных исследований и опытно-конструкторских разработок (НИОКР).

Результаты исследования.

Для этого предположим, что в секторе производства реализуется совершенная конкуренция, а значит, все НПК (фирмы, предприятия, корпорации и их объединения [4], интересы которых финансово согласованы [5]) первоначально обладают возможностью использовать одну и ту же современную технологию и в расчете на одно изделие производят наукоемкую продукцию с неизменными предельными издержками с . Так же предположим, что в сфере НИОКР имеет место олигополистическое равновесие, которое характеризуется постоянными затратами на разработку прогрессивной наукоемкой продукции различного назначения. В этих условиях будет справедливым полагать, что:

• -    все субъекты НПК конкурируют между собой за создание инновации (государственную регистрацию и получение патента), которая после этого лицензируется;

• -    внедрение инновации повлечет за собой сокращение производственных издержек НПК до уровня (с - d) , где d - выручка владельца патента за каждое изготовленное изделие.

Введем следующие обозначения:

H - доход обладателя инновационного патента, полученный за весь срок его действия;

J - рост общественного благосостояния (если он имеет место), обусловленный использованием инновации за весь временной период действия патента (он не может быть присвоен обладателем патента, но может использоваться потребителями и другими производственными объединениями);

K - безвозвратные потери, происходящие в течение временного периода действия патента, поскольку потенциальный рост общественного благосостояния может начаться только после завершения времени действия патента, а в период действия патента благосостояние не повышается из-за монополистического владения дополнительными доходами обладателем патента).

Предположим, что H , J u K являются стационарными потоками. Тогда величина H всегда положительна, а величины J и K больше или равны 0 ( J >  0 и K >  0) .

Для характеристики спроса введем функцию Q(P). Будем считать инновацию радикальной в том случае, когда монопольная цена, обусловленная новыми (уменьшенными) предельными издержками (с-d), становится ниже, чем соответствующая прежним предельным издержкам с. Имитацию инновации (запатентованной технологии) можно рассматривать как создание НПК собственной технологии, созданной на основе информацион- ных данных о конечном изделии, которое было произведено при использовании запатентованной технологии, и, как правило, по качеству уступающей запатентованной [6, 7]. В том случае, когда инновация не может считаться радикальной и имитировать ее нельзя, обладатель патента должен лицензировать новую инновационную технологию с оплатой за единицу выпускаемого изделия равной d. В этой ситуации для достижения постинновационного равновесия выпуск изделий останется на начальном (доинновационном) уровне Q0 = Q(c), и доход собственника патента определяется произведением стоимости доинновационного выпуска и уменьшения издержек производства d. На рис.1 этот доход представлен графически как площадь прямоугольника H.

Свободный доступ к прогрессивной технологии открывается, когда временной период действия патента заканчивается, при этом уровень выпуска продукции возрастает до Q 1 = Q(c - d) , а цена определяется величиной новых существенно сниженных предельных издержек [8]. При этом безвозвратная потеря, которая обусловлена лицензированием патента, графически соответствует площади треугольника K (см. рис. 1). Таким образом, в случае нерадикальной инновации владелец патента в полном объеме присваивает себе инновационную общественную выгоду в течение всего лицензионного периода, а J=0 .

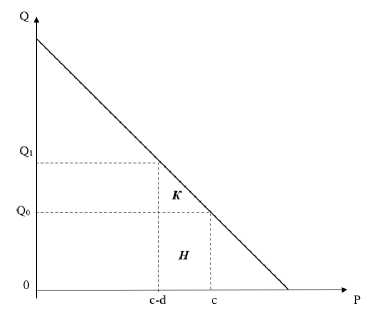
Рис. 1. Нерадикальная инновация

В случае радикальной инновации обладатель патента выдает лицензии на использование новой инновационной техно- логии заинтересованным НПК, взимая при этом платеж, графически соответствующий площади прямоугольника H (см. рис.

• 2). При этом основное отличие от рассмотренного ранее случая состоит в том, что некоторая часть роста общественного благосостояния, получаемая обществом до окончания временного периода действия патента, обладателем патента не присваивается [9]. На рис. 2 эта часть графически соответствует площади фигуры J .

Аналогичная ситуация возникает и тогда, когда патент обладает очень длительным временным периодом, а НПК не способны имитировать новый инновационный технологический процесс. Уровень издержек субъектов НПК останется при этом на доинновационном уровне, равном с. Но если временные границы патента окажутся узкими, то субъекты НПК могут имитировать инновацию, не нарушая лицензион- ных условий патента, и в некоторой степени уменьшить свои издержки. Мерой временных периодов действия патента служит доля снижения производственных издержек, которая не передается НПК как бесплатно доступная технология. Поэтому, обозначив пределы действия патента через γ, можно формализовать предельные издержки НПК, имитирующих новую инновационную технологию, следующим образом - (c—Yd). В результате получаем J>0, что и будет отражать разницу между частной и общественной выгодой от создаваемой и применяемой инновации в течение всего временного периода действия патента.

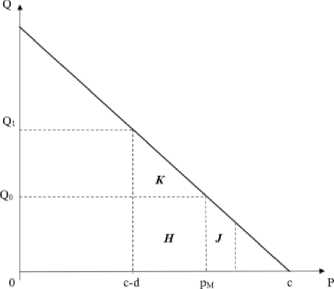
Рис. 2. Радикальная инновация

С момента T , который соответствует завершению временного периода действия патента, равновесная цена падает до значения (c - d) , а общественное благосостояние увеличится на величину К .

Используя введенные обозначения и учитывая приведенные выше рассуждения, можно перейти непосредственно к разработке модели конкуренции субъектов НПК, возникающей на начальных этапах инновационного процесса. В сфере НИОКР при создании патентоспособной инновации происходит конкуренция между несколькими субъектами НПК. В момент времени t=0 каждый конкурирующий участник определяет объем НИОКР X i и производят единовременные исследовательские затраты a x i , где а - предельные

(допустимые) затраты на выполнение программы НИОКР. Объем НИОКР позволяет рассчитать временной период, необходимый для успешного выполнения всех запланированных научно-исследовательских работ. Предполагая, что срок создания инновации i-ым субъектом НПК распределен экспоненциально и при этом не зависит от времени разработки инновации другими субъектами НПК, вероятность удачного завершения всего комплекса работ i-ым субъектом НПК в момент времени t или раньше составляет (1 - a ^{- xit} ) . Функция выигрыша s i субъекта i ( i=1,...,n ) представляет собой величину ожидаемых доходов без затрат на выполнение комплексной НИОКР, т.е.:

∞n si = Г exp[-(^ x. + r)t ]x Vdt - ax 0           j=1

где r – процентная ставка;

V – реальная стоимость доходов, кото рые получает i-ый субъект НПК;

αxi – переменные издержки, связанные с выполнением НИОКР;

F – постоянные издержки, связанные с выполнением НИОКР.

В момент t=0 выплачиваются и переменные, и постоянные издержки.

• - F = _n ^xiV   - α x_i - F ,             (1)

∑ x j + r j = 1

n

Величина exp[ - ( ∑ x )t] есть вероят- j = 1

ность процесса, при котором к моменту времени t ни один из субъектов НПК не смог разработать запланированную инновацию.

Доход V обладателя патента определяется дисконтированными доходами от лицензирования запатентованной технологии:

T

V = ∫ H α ^{- rT} dt = zH/r ,

-rT где z = 1-α r – величина дисконтированных доходов H/r, получаемая обладателем патента.

Каждый субъект НПК выбирает такой вариант инвестирования в НИОКР, который максимизирует ожидаемые доходы (1). Необходимое условие максимума можно представить следующей формулой:

( X - + r V

( r + X - + x j²

n где  X-i=∑xj .

j ≠

Нетрудно показать, что данное условие выполняется. Для этого предположим, что все субъекты НПК идентичны, и исследу- ем симметричное равновесие, характеризуемое соотношением xi = x для всех i. В этом случае условие (3) принимает вид:

[( n - 1) r + r ] V ( r + r a )²

При дальнейшем рассмотрении проблемы будем предполагать, что все субъекты НПК имеют возможность выполнять НИОКР. Тогда число таких субъектов в исследуемом секторе эндогенно и прибыль для них становится нулевой:

rV

- α x - F = 0 . nx + r

Уравнения (4) и (5) определяют равновесное число субъектов НПК n и x : (nx+r)² = x²V/F .

Подставляя это выражение в уравнение (5), получаем

x = ( FV - F )/ α ;

n =

ra

.

V FV - F

При этом равновесное число количество субъектов НПК в отрасли становится убывающей функцией, зависящей от постоянных издержек НИОКР F. При F^ 0 сектор научных исследований превращается в совершенно конкурентный.

Интегральное     инвестирование в

НИОКР X=r a составляет:

X = -( zH -a r

zFH r

) ^- r .

Но даже при гарантии максимальной защиты патента проводимая государством патентная политика станет неэффективной, если институты, регулирующие и стимулирующие инновационную экономическую деятельность, не будут осуществлять необходимое инвестирование НИОКР, выполняемых НПК [1]. Поэтому будет логичным предположить, что беско- нечный период действия патента увеличивает инвестирование и приводит к ситуации, когда X>0. Обозначив через T минимальный период действия патента, при котором происходит равновесное и положительное инвестирование в НИОКР, и

-rT z = 1 - a , получим, что r z = —

H

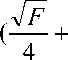
F

J— + ar )² 4 4

Далее, предположим, что z < 1. Это предположение требует выполнение следующего неравенства:

H FF

— > (---+ J—+ a r )².

r 4 V 4

В предельном случае, когда F = 0 , это неравенство сводится к следующему виду:

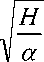
Заключение.

Разработанная модель конкуренции субъектов НПК учитывает практически всю совокупность факторов и затрат, оказывающих влияние на эффективность инновационных продуктов и технологий на начальных и последующих этапах инновационного процесса. Представляется, что использование этой модели будет полезным для различных наукоемких производственных комплексов при анализе эффективности осуществляемых ими инноваций.

• > r .                                              (11)

Статья подготовлена при финансовой поддержке Российского фонда фундаментальных исследований, проект № 19-01000043 «Теоретические основы, инновационные методы и организационноэкономические механизмы создания и рыночной реализации отечественной наукоемкой продукции в условиях глобализации экономики и расширения антироссийских санкций».