Модель локализации объектов на цифровом изображении

Проблему локализации можно охарактеризовать как проблему разбиения обрабатываемого изображения на изображения объектов, подлежащие дальнейшему признаковому анализу и идентификации автоматической системой распознавания. Из-за недостаточной формализации понятия «изображение» в настоящее время данная проблема относится к числу недостаточно формализованных и обычно рассматривается для изображений из заданной предметной области или решается в контексте распознавания заданных объектов. Тем не менее в случае простейших изображений объектов на однородном фоне она, как правило, не возникает. Поэтому имеет непосредственный смысл разработка алгоритмов, которые позволили бы установить взаимосвязь решения общей проблемы локализации объектов с решением частной задачи их выделения на однородном фоне.

Целью статьи является обсуждение вычислительной модели локализации объектов на цифровом изображении, разработанной в предположении иерархической природы объектов посредством обобщения и развития вычислений в методах Оцу [1-3], модели Мамфорда–Шаха [4-10] и методе K – средних [11-19], реализуемых на современных компьютерах.

1. Постановка задачи

Перечисленные подходы, в отличие от большинства других подходов к выделению объектов на цифровых изображениях, наиболее формализованы по постановке задачи, так как при построении разбиений опираются на определенный критерий качества. Критерием качества в методах Оцу и методе K –средних, а также в версии [7] модели Мамфорда–Шаха служит суммарная квадратичная ошибка E , или равносильная величина среднеквадратичного отклонения σ значений пикселей изображения от значений пикселей оцениваемого кусочно-постоянного приближения.

Метод Оцу [1-3] является одним из немногих, если не единственным методом точного вычисления оптимальных приближений, минимально отличающихся от изображения по суммарной квадратичной ошибке. Это классический метод кластеризации пикселей изображения посредством нахождения по яркостной гистограмме одного или нескольких пороговых значений яркости, которые разбивают шкалу яркости на диапазоны из условия минимального значения среднеквадратичного отклонения средних по диапазонам значений пикселей от значений пикселей исходного изображения. В методе Оцу одинаковые пиксели изображения всегда относят к одному кластеру, состоящему из некоторого числа сегментов (связных областей) изображения. То, что метод Оцу не позволяет относить одинаковые пиксели к различным кластерам, препятствует его использованию для локализации объектов посредством классификации пикселей в зависимости от особенностей их локального распределения. Принципиальным ограничением метода Оцу является то, что он не имеет очевидного обобщения на случай классификации многомерных пикселей цветовых или многоспектральных изображений.

Метод K –средних является старейшим методом многомерного кластерного анализа [17-18] и интенсивно применяется не только в обработке изображений, но также и в ряде других областей, связанных с классификацией и распознаванием данных. В приложении к изображениям он сводится к итеративной коррекции разбиений пикселей на кластеры или сегменты посредством реклассификации пикселей из условия минимизации расстояния до центроидов в виде векторов (столбцов), покомпонентно усредненных по кластерам яркостных значений. В учебной и научной литературе принято обсуждать метод K –средних без предварительного аналитического обоснования. Между тем элементарные выкладки, приводимые в следующем разделе, показывают, что минимизация расстояний до центроидов кластеров не равносильна минимизации суммарной квадратичной ошибки. Поэтому для оптимизации приближений вместо метода K –средних оказывается эффективным применять метод коррекции разбиений в уточненном варианте [19].

Традиционная модель Мамфорда–Шаха [4-9] относится к теоретически и экспериментально обоснованным моделям сегментации изображения посредством итеративного слияния сегментов. Отождествление классов со связными сегментами, однако, ограничивает возможность отнесения пикселей экземпляров объекта и частей объекта к одному классу. Условие связности пикселей поддерживается в модели автоматически, благодаря использованию единственной операции слияния смежных сегментов, которая не выводит из их множества. С другой стороны, использование единственной операции слияния сегментов при последовательной генерации разбиений изображения опирается на предположение, что последовательность оптимальных разбиений изображения является иерархической. Поскольку последовательность разбиений изображения, минимизирующих E или а , вообще говоря, отличается от иерархической [10], единственность операции слияния сегментов является принципиальным недостатком вычислений в традиционной модели Мамфорда–Шаха [4-9], который полезно исправить.

Характерной особенностью обсуждаемых классических методов сегментации изображений посредством оптимизации качества разбиений по суммарной квадратичной ошибке E или среднеквадратичному отклонению а является прозрачность алгоритмов и необходимых вычислительных формул, которая часто утрачивается в многочисленных приложениях при эвристическом учете свойств «объектов интереса» и оптимизации итерационных вычислений по скорости. При этом постановочное условие оптимизации качества разбиений по E (или а ) обычно не контролируется в качестве обязательного критерия достоверности вычислений. В отличие от большинства практических решений для конкретных предметных областей, мы строим унифицированный алгоритм локализации объектов только на основании элементарных аналитических соотношений, непосредственно связанных с минимизацией целевого функционала.

A E

merge

II 1 1 - I 2II²

11 — +-- n1   n2

где знак || ||² обозначает суммирование квадратов отклонений I_x - I ₂ (евклидову норму векторов по цветовым или спектральным компонентам).

В случае k < n_x предусматриваются две возможные операции реклассификации подмножества пикселей кластера 1 – дробление и коррекция.

При операции дробления кластера надвое k пикселей из кластера 1 выделяются в новый кластер. При этом кластер 1 преобразуется в кластер из n_x - к пикселей, которые дополняли обсуждаемые к пикселей в составе прежнего кластера. Операция дробления кластера сопровождается отрицательным, или нулевым, приращением суммарной квадратичной ошибки AE_spUt :

A E split =

III -1112

< 0.

k

n ₁

При операции коррекции часть пикселей реклассифицируется из кластера– донора 1 в акцепторный кластер 2, что сопровождается приращением суммарной квадратичной ошибки AE_correct :

KE correct

II I — 1 2 Г I I — 1 1112 ----

11  11

- + —  --- k n2 k n1

При этом второе, отрицательное, слагаемое в (3) описывает приращение суммарной квадратичной ошибки при выделении k пикселей из кластера 1 в самостоятельный кластер, а первое слагаемое описывает ее приращение при слиянии выделенного кластера с кластером 1 согласно (1) и (2). Таким образом, операция коррекции трактуется как составная.

Из (3) получаем для коррекции критерий убывания суммарной квадратичной ошибки E :

|| I - 1 JI >  a -I | - 1 2||,                                      (4)

где коэффициент a <  1 описывает соотношение количества пикселей в рассматриваемых кластерах 1,

2 и выражается в виде:

n,(n, - k)

a =   —^{2 v 1}-----

Ч П1 (n 2 + k)

Если коэффициент a в формуле (4) положить равным 1, то из нее выводится метод ^ -средних. Однако если не делать этого упрощения, которое практически не влияет на скорость вычислений на современных компьютерах, то, опираясь на формулу (4) с учетом коэффициента a , удается получить более сильный метод реклассификации пикселей [19]. Он позволяет избегать преждевременного останова минимизации суммарной квадратичной ошибки, точнее выбирать варианты реклассификации пикселей и эффективнее снижать величину суммарной квадратичной ошибки за счет реклассификации не отдельных пикселей, а их множеств.

попарного объединения сегментов до их слияния в один кластер. При этом для каждого сегмента, как для отдельного изображения, выполняется укрупнение вложенных смежных сегментов в модели Мамфорда–Шаха [7, 10], очередная пара которых выбирается по критерию слияния, которым служит минимальная величина       :

merge

^ E merge = min ,                               ⁽⁶⁾

а затем тот же самый критерий применяется для объединения сегментов посредством вычисления значений №_meTge для каждой пары сегментов, составляющих рассматриваемый кластер. В целом для каждого кластера из p пикселей обсуждаемая бинарная иерархическая последовательность разбиений задает 2 p - 1 составных частей (вложенных кластеров, сегментов и их связных компонент).

Для детализации разбиения изображения посредством дробления кластера на составную часть и ее дополнение используется формула (2). Критерием служит условие максимального падения суммарной квадратичной ошибки, т. е. ее минимального приращения kE_Ut :

^split = min .                               ⁽⁷⁾

В результате дробления кластера общее число кластеров увеличивается на единицу, а число сегментов увеличивается или остается прежним.

Формула (3) применяется для итеративного снижения суммарной квадратичной ошибки посредством циклически повторяемой коррекции пар кластеров. Выполняется до тех пор, пока на изображении обнаруживаются кластер-акцептор и кластер-донор, имеющий смежную с кластером-акцептором составную часть, реклассификация которой в кластер–акцептор приводит к падению суммарной квадратичной ошибки. Из множества вариантов требуемой реклассификации выбирается вариант, сопровождаемый минимальным приращением суммарной квадратичной ошибки kE_correct:

^correct = ^min <  ⁰ •                          ⁽⁸⁾

В процессе коррекции разбиения изображения на кластеры общее число кластеров не меняется. Если при коррекции реклассифицируемая составная часть кластера–донора содержит единственный сегмент, то число сегментов в кластере–акцепторе также остается прежним.

В результате коррекции получается устойчивое разбиение изображения на кластеры, которое нельзя улучшить по суммарной квадратичной ошибке посредством реклассификации составной части любого кластера в другой, смежный с этой частью.

Если в изложенной схеме коррекции разбиения изображения на кластеры допускается реклассификация любой части кластера–донора, необязательно смежной с кластером–акцептором, то такая коррекция называется безусловной . При безусловной коррекции разбиения изображения число кластеров сохраняется, но возрастает число сегментов в кластерах–акцепторах за счет слияния кластеров–акцепторов с несмежными составными частями кластеров–доноров. В результате безусловной коррекции получается разбиение изображения на кластеры, которое нельзя улучшить по суммарной квадратичной ошибке посредством реклассификации любой предусмотренной составной части одного кластера в другой.

Вычисления проводятся в алгоритме «наращивания кластеров», в котором коррекция разбиения изображения выполняется по очереди с увеличением числа кластеров на единицу за счет дробления кластера, отвечающего максимальному падению суммарной квадратичной ошибки. При этом генерируется последовательность устойчивых разбиений изображений на кластеры для любого начального разбиения (например, содержащего единственный сегмент, покрывающий все изображение) или для начального разбиения изображения на несколько сегментов. Во втором случае применение вместо дробления кластеров безусловной коррекции обеспечивает детализацию начального разбиения изображения за счет увеличения числа сегментов при неизменном числе кластеров.

Таким образом, в нашей интерпретации, локализация объектов реализуется благодаря вычислению последовательности кусочно-постоянных приближений изображения, порождаемых его устойчивыми разбиениями на кластеры. Кластеры пикселей изображения разделяются на составные части, образуемые сегментами (связными областями) изображения. При построении устойчивых разбиений кластеры обмениваются сегментами из условия снижения суммарной квадратичной ошибки E или среднеквадратичного отклонения ст . В процессе построения устойчивого разбиения при модифика-185

ции кластеров обновляется и сопоставляемая каждому кластеру иерархия его составных частей. Поэтому устойчивые кластеры пикселей изображения характеризуются не только устойчивостью относительно обмена составными частями друг с другом, но и соответствием составных частей целостным кластерам.

• 4.    Экспериментальные результаты

Экспериментальные результаты по локализации объектов в графическом виде демонстрируются на рис. 1.

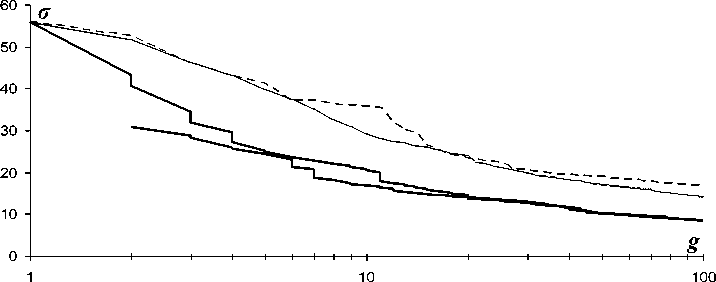
Рис. 1. Оценка качества разбиения в зависимости от числа кластеров

Рис. 1 на примере стандартного изображения «Лена»¹ иллюстрирует среднеквадратичное отклонение т изображения от его кусочно-постоянных приближений в зависимости от числа кластеров g , которое совпадает с числом градаций средней яркости. Графики изображены в логарифмическом масштабе по горизонтальной оси в диапазоне числа кластеров от 1 до 100.

Две верхних переплетающихся кривых описывают иерархические разбиения на сегменты, полученные по версии FLSA модели Мамфорда–Шаха [8, 9] (верхняя штрихованная кривая) и по версии [7] (сплошная серая кривая). Они отражают известные результаты и приведены для наглядной демонстрации эффекта снижения среднеквадратичного отклонения т при генерации устойчивых разбиений.

Пара нисходящих сливающихся друг с другом черных кривых описывает процесс автоматической генерации последовательности устойчивых разбиений изображения посредством чередования увеличения числа кластеров на 1 за счет дробления одного из них и циклической коррекции разбиения до преобразования его в устойчивое разбиение изображения. Верхняя кривая соответствует случаю тривиального начального разбиения, содержащего единственный кластер. Нижняя кривая соответствует начальному разбиению изображения на два кластера из нескольких сегментов. При этом каждому значению числа кластеров g на той и другой кривой соответствуют по две точки, которые для отдельных значений g на графиках разделяются, а для большинства остальных сливаются между собой, т. к. незначительно различаются по т . Устойчивые разбиения изображения описываются для каждого значения g минимальным значением т .

Отрезок вертикальной пунктирной прямой на рис. 1 начинается от минимального значения т для g = 2 на верхней нисходящей кривой. Он описывает циклическую детализацию соответствующего инвариантного разбиения изображения по числу сегментов при неизменном числе кластеров в алгоритме безусловной коррекции. В результате безусловной коррекции получается устойчивое разбиение изображение на два кластера, которое характеризуется значением среднеквадратичного отклонения, равным т = 30.64564 . Характерно, что полученное разбиение совпадает с оптимальным разбиением изображения на два кластера пикселей [3, 7], которое вычисляется классическим методом Оцу [1]. Фактически обсуждаемый отрезок представляет 182 точки, сгущающиеся по мере приближения к оптимальному значению. При этом плавное снижение σ наглядно выражается в проявлении шумов на соответствующих кусочно–постоянных приближениях изображения. Поэтому для испытания алгоритма поочередного дробления и коррекции при нетривиальном начальном разбиении изображения (нижняя нисходящая кривая на рис. 1) в качестве начального устойчивого разбиения выбрано не оптимальное разбиение, а разбиение, полученное с подавлением шумов, которое получается на 11-й итерации безусловной коррекции и отвечает значению σ = 30.79373 .

Для уточнения данных первые десять пар численных значений σ (для верхней нисходящей кривой) и σ ′ (для нижней нисходящей кривой), отвечающие устойчивым разбиений изображения, перечислены для последовательных значений числа кластеров g в таблице 1 (по пять штук в каждой колонке).

Таблица

Значения σ и σ ′ для последовательных разбиений изображения

№	g	σ	σ ′
1	1	55.88322
2	1	55.88322
3	2	43.16748	30.79373
4	2	40.58435	30.79373
5	3	34.39798	28.72376
6	3	31.85193	28.08163
7	4	29.55488	25.85536
8	4	27.04307	25.73018
9	5	25.09586	24.31218
10	5	24.86835	24.21468

№	g	σ	σ ′
11	6	23.62842	22.93591
12	6	23.51916	21.17198
13	7	22.82637	20.56156
14	7	22.73704	18.64853
15	8	22.05335	18.04458
16	8	21.99891	18.01739
17	9	21.39022	17.43846
18	9	21.25647	17.19645
19	10	20.59120	16.82263
20	10	20.55978	16.77930

Значения среднеквадратичного отклонения, указанные в таблице 1 в строках с четными номерами, отвечают устойчивым разбиениям изображения. Сами устойчивые разбиения, которые наглядно описываются посредством кусочно-постоянных приближений изображения, представлены на рис. 2.

Рис. 2. Устойчивые разбиения изображения

В правом верхнем углу рис. 2 показано стандартное изображение «Лена». В первой колонке демонстрируются устойчивые разбиения изображения с числом кластеров от одного до пяти, полученные чередованием дробления очередного сегмента и циклической коррекции при тривиальном начальном разбиении изображения, отвечающего значению σ = 55,88322. Во второй колонке показаны устойчивые разбиения, полученные по тому же алгоритму, но при нетривиальном начальном разбие- нии изображения, которое отвечает значению σ = 30.79373 и размещено под стандартным изображением.

Графически последовательность разбиений рис. 2 описывается огибающими каждой из черных сливающихся кривых на рис. 1, которые строятся по точкам с меньшими значениями σ . По поводу рис. 2, следует заметить, что вычисляемые для кластеров значения средней яркости являются вещественными числами, которые при визуализации округляются до целых и могут не различаться при печати.

• 5.    Интерпретация

Исходя из результатов эксперимента, можно утверждать, что по сравнению с традиционной моделью Мамфорда–Шаха, предложенная модель локализации объектов на цифровом изображении обеспечивает заметное улучшение кусочно-постоянных приближений по среднеквадратичному отклонению σ , (рис. 1), причем, без резкого увеличения числа сегментов, как в методе Оцу [3, 7]. При этом улучшение качества приближений наглядно выражается в более полном и точном «проявлении» объектов в приближениях изображения с ограниченным числом градаций яркости (рис. 2).

Характерно, что при генерации разбиений в алгоритме «наращивания кластеров» от различных начальных разбиений изображения, различие по σ результирующих устойчивых разбиений нивелируется, и соответствующие кривые на рис. 1 сближаются друг с другом, по-прежнему, заметно выигрывая по σ у традиционной модели. На изображении при этом выделяются сходные совокупные наборы объектов.

Отличительной особенностью пары сливающихся кривых на рис. 1, описывающих процесс получения последовательности устойчивых разбиений изображения, является наличие участков плавного снижения среднеквадратичного отклонения σ , разделенных его резкими перепадами. Резкое снижение σ описывает существенное изменение очередного разбиения изображения при модификации нескольких кластеров и заметном смещении их границ, как в верхних четырех приближениях слева на рис. 2. Плавное снижение σ описывает последовательное проявление на изображении очередного объекта при незначительной модификации границ, как в колонке приближений справа на рис. 2, размещенных под исходным изображением. Последнее дает основание предположить, что изображение имеет «кусочно–иерархическую» структуру, т.е. аппроксимируется последовательностями иерархических приближений по диапазонам кластеров, которые можно вычислить, детектируя участки плавного снижения среднеквадратичного отклонения σ на графиках рис. 1. По нашему мнению, сформулированная гипотеза представляет самостоятельный интерес для дальнейшего теоретического и экспериментального исследования.

Заключение

Таким образом, в настоящей статье мы развиваем оптимизацию приближений изображения для локализации и выделения объектов на основе модели Мамфорда–Шаха [7], в которой из соображений минимизации суммарной квадратичной ошибки E (среднеквадратичного отклонения σ ) утроили число операций с множествами пикселей и перешли от вычислений со связными сегментами к вычислениям с кластерами из несмежных сегментов, порождаемыми дополнительными операциями дробления и коррекции кластеров пикселей изображения. Для оптимизации разбиений изображения по E (или σ ) разработан и испытан алгоритм «наращивания» кластеров, аналитически выведенный из условий минимизации суммарной квадратичной ошибки (1)-(3) и (6)-(8), в котором именно соображениями минимизации целевого функционала определяется как порождаются кластеры, как они разделяются на составные части, а также как обмениваются составными частями друг с другом. При этом для минимизации функционала с сохранением числа кластеров применен метод многомерной кластеризации, который по эффективности превосходит метод K -средних, а в одномерном случае обеспечивает воспроизведение результатов, полученных классическим методом Оцу [1], что позволяет применять этот метод в качестве многомерного аналога метода Оцу.

В настоящее время продолжаются работа по совершенствованию предложенной модели и ее применению для унификации автоматической локализации и выделения объектов на цифровых изображениях [20].