Модель мемристоров Бернулли в виде полинома расщепленных сигналов
Автор: Соловьева Елена Борисовна, Гарчук Анна Александровна
Рубрика: Краткие сообщения
Статья в выпуске: 3 т.13, 2020 года.
Бесплатный доступ
В работе представлена поведенческая модель мемристора, в котором динамика тока описывается дифференциальным уравнением Бернулли. Поведенческая модель построена в виде двумерного полинома расщепленных сигналов для передаточной характеристики мемристора Бернулли при гармоническом входном сигнале. Расщепление входных сигналов обеспечивает однозначность соответствия вход-выход, адаптацию модели к заданному классу воздействий и, следовательно, ее простоту по сравнению с универсальными нелинейными моделями, например, рядом Вольтерры и нейронными сетями. Расщепление гармонического воздействия выполнено с помощью линии задержки. Показано, что векторный сигнал, содержащий воздействие и результат его задержки во времени на один шаг, обладает минимально возможной длиной согласно условиям расщепления. Двумерный полином третьей степени, построенный на элементах векторного сигнала, обеспечивает высокую точность моделирования передаточной характеристики мемристора Бернулли в среднеквадратичной метрике.
Мемристор, нелинейная динамическая система, поведенческая модель, многомерный полином
Короткий адрес: https://sciup.org/147232995
IDR: 147232995 | УДК: 519.65+621.3.01 | DOI: 10.14529/mmp200309
Текст краткого сообщения Модель мемристоров Бернулли в виде полинома расщепленных сигналов
Область применения математических моделей, описывающих соотношение вход-выход (или поведенческих моделей) нелинейных динамических систем (НДС) неуклонно расширяется в результате появления новых форм моделей, разработки новых элементов, устройств, систем, а также технологий и материалов их реализации [1, 2]. Активно развивающимися динамическими системами являются мемристив-ные системы, построенные на мемристорах. Мемристор (memory resistor, резистор с памятью) – четвертый электрический элемент (три другие: резистор, емкость, индуктивность), сопротивление которого нелинейно зависит от истории тока, протекающего через него. Область применения мемристивных систем обширна [1–3]: аналоговые устройства различного назначения; нейронные сети; преобразователи изображений; нейроморфные системы; самонастраивающиеся аналого-цифровые устройства управления; энергонезависимые запоминающие устройства; системы программируемой логики. С развитием мемристоров связана разработка моделей, описывающих разнообразные физические и технологические механизмы построения мемристивных систем [3].
Актуальной остается задача получения простых математических моделей. Такую возможность дают модели, рассматриваемые в рамках теории расщепления сигналов [4,5]. Согласно теории расщепления оператор нелинейного устройства представляется композицией двух операторов: оператора расщепителя и оператора нелинейного безынерционного преобразователя. Оператор-расщепитель преобразует скалярные входные сигналы в векторные так, чтобы фазовые портреты векторных сигналов не пересекались, не касались и не проходили через ноль. Полученные векторные сигналы называются расщепленными. Оператор нелинейного безынерционного преобразователя отображает векторные сигналы в скалярные выходные сигналы. Математические формы преобразователя различны, например, полиномы, дроби, нейронные сети [4,5].
1. Математическое моделирование мемристоров Бернулли методом расщепления
Рассмотрим построение поведенческой модели в виде многочленов расщепленных сигналов для мемристоров Бернулли. Данные мемристоры, управляемые зарядом и возбуждаемые напряжением, описываются парой уравнений [6]:
dq ( t ) = v( t ) = dq( t )
dt M (q(t)), i ( t ) dt
где q(t) - заряд (управляющий сигнал или переменная состояния мемристора); v(t), i(t) - напряжение (входной) и ток (выходной) сигналы соответственно; M(q(t)) -мемристанс.
Мемристор Бернулли получил свое название в силу того, что динамика тока мемристора определяется из дифференциального уравнения Бернулли [6–8]:
di(t) dv(t)/dt k 2 ,a+2
dt v(t) i( t ) = v(t) i
где a = — 1, — 2 - целое число, k 2 =
dM (q(t)') dq(t)
переменная, связанная с физической
структурой мемристора. Динамика мемристанса описывается уравнением [7, 8]:
5“^ = k2i a ( i ) = - ' , a ( < ) .
dt 2 v ! dq(t) ’
Частотные характеристики мемристоров определяются при гармонических воздействиях, записанных, например, в виде
v(t) = x(A,t) = A sin(t),
где t E [0, 2п) - нормированное непрерывное время.
Известно решение уравнения (1) при воздействии (2) в аналитической форме [7,8]:
i ( t ) =
v ( t )
Г t l1/(a + 1) ’
M o 1 + в 2 J v a (T)dT\
где M o = v(0)/i(0), в 2 = (a + 1)k 2 A/M 0 a+1 .
Для формирования множества выходных сигналов мемристора используем выражение (3) с заданными переменными. Например, при a = 1 и воздействии (2) преобразуем равенство (3) к виду [7, 8]:
i ( t ) =
v^
M 0 [1 + в 2 (1 — CO^tD)] 1 / 2
далее при Mg = 2, k2 = 2 получим в2 = A и перейдем от выражения (4) к формуле ад =-----v®—.
2[1 + A (1 - cos®)] 1 / 2
Таким образом, выходной сигнал i(t) мемристора при воздействии v(t) формируется из выражения (5) и применяется для поведенческого моделирования мемристора Бернулли.
По соотношению вход-выход (5) мемристора построена поведенческая модель в виде многочлена расщепленных сигналов. В процессе моделирования выполнены следующие операции:
– сформированы три векторных сигнала:
X si (A, t) = [x(A, t)] = [A sin(t)], (6)
X s 2 (A,t) = [x si (A,t), X s2 (A,t)] T = [A sin(t), A sin(t - t o )] T , (7)
X sa (A,t) = [x si (A,t), X s2 (A,t), X sa (A,t)] T =
= [A sin(t), A sin(t — t0), A sin(t — 2t0)] , где tg - смещение в нормированном времени;
– на базе указанных векторов записаны следующие формы многомерных полиномов:
J 1
У1№ = Е C” [x (A,'01 j1 ■(9)
J 1 J 2
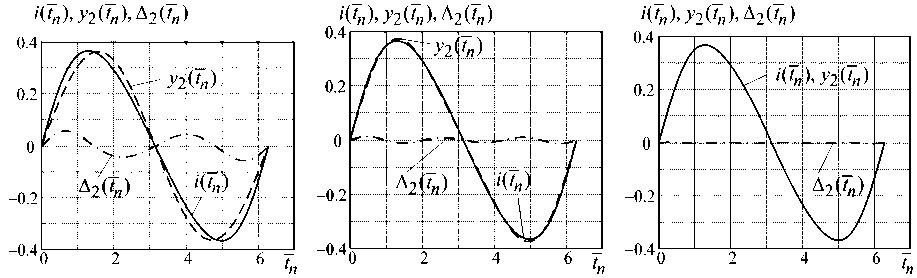
y2 j1=o j2=0 J1 J2 J3 ya(t) = 52 52 52Cjij2j3 [xsi (a,/)] j1 [xs2 (a,/)] j2 [xs3 (a^ j3. j1=0 j2=0 j3=0 степеней J = J1, J = ^ Jr, J = 5УJr соответственно; r=1 – в результате решения задачи аппроксимации: ||i(t) -у/y(t)^ ^ min ?Y = 1-2-3, te[0,2n) где i(t) - выходной сигнал мемристора из формулы (5), в среднеквадратичной метрике определены параметры полиномов (9) – (11). Для оценки точности построенных моделей (9) – (11) вычислены: равномерная погрешность Ay (tn)= i(tn) - yY (tn), n = 1, 2-..., 628, Y = 1, 2, 3, (12) где tn - значения нормированного времени в интервале tn G [0, 2п), меняющиеся с временным шагом 0, 01; максимальная абсолютная и среднеквадратичная погрешности соответственно: ^y = _max (|i(tn) - yY(tn)|), n = 1, 2,..., 628, y = 1, 2, 3, tn e[0,2n) Q = А 1Е( i(tq) - yY(tq)) 2, q=1 Q = 628, y = 1, 2, 3. Результаты моделирования мемристора представлены при входном сигнале (2) с амплитудой A = 1. Анализируя результаты моделирования, проиллюстрируем необходимость расщепления входных сигналов. На рис. 1, а), б) представлены зависимости максимальной абсолютной (57) и среднеквадратичной (ey ) погрешностей от степени J многомерных полиномов (9) – (11). а) б) Рис. 1. Зависимости максимальной абсолютной (а) и среднеквадратичной (б) погрешностей от степени J полиномиальных моделей мерности γ Из анализа рис. 1 а) и 1 б) следует: - линейные модели (J = 1) разной мерности (y = 1, 2, 3) дают одинаковые погрешности моделирования, наибольшие по сравнению с нелинейными моделями; – двумерный и трехмерный полиномы обеспечивают одинаковые погрешности моделирования мемристора, погрешности уменьшаются с увеличением степени моделей. Следовательно, входной сигнал (2) с амплитудой A = 1 расщепляется при формировании векторных векторов (7) и (8). Отметим, что этот факт доказывается аналитически на основе условий расщепленности сигналов из теории расщепления. Очевидно, что сложность модели возрастает не только с увеличением степени полинома, но и с ростом ее мерности в пространстве. Для простоты модели следует выбирать минимальную мерность полинома, т. е. минимальное число каналов расщепления. В рассматриваемом примере при воздействии (2) в качестве расщепленного сигнала целесообразно использовать вектор (7) и модель – двумерный полином расщепленных сигналов (10). Наглядно результаты математического моделирования мемристора Бернулли показаны на рис. 2 и рис. 3. На рис. 2 а), 2 б), 2 в) изображен выходной сигнал мемристора i(tn) из формулы (5), выходные сигналы y2(tn) модели - двумерного полинома расщепленных сигналов (10) и равномерные погрешности моделирования Л2(tn), вычисленные по формуле (12) при 1-й, 2-й и 3-й степенях (J = 1, 2, 3) модели (10) соответственно. На рис. 3 а), 3 б), 3 в) показаны гистерезисные передаточные характеристики, построенные в виде зависимостей сигнала i(tn) (выходного сигнала мемристора из формулы (5)) и сигналов y2(tn) (выходных сигналов модели (10) при 1-й, 2-й и 3-й степенях двумерной а) б) в) Рис. 2. Выходные сигналы мемристора Бернулли и его двумерной полиномиальной модели 1-й (а), 2-й (б) и 3-й (в) степени, а также соответствующие равномерные погрешности моделирования а) б) в) Рис. 3. Графики передаточных характеристик мемристора Бернулли при моделировании двумерным полиномом 1-й (а), 2-й (б) и 3-й (в) степеней нелинейности соответственно) от воздействия v(tn) из выражения (2) при A = 1. Из рис. 2 и рис. 3 следует, что двумерный полином расщепленных сигналов (10) 3-й степени дает наибольшую точность моделирования мемристора Бернулли при воздействии (2) с амплитудой A = 1. Заключение Математические модели мемристоров предложено строить в виде полиномов расщепленных сигналов. Свойство расщепления обеспечивает однозначное соответствие между множеством входных и выходных сигналов динамических систем. Сложность модели зависит не только от степени ее нелинейности, но и от формируемого вектора расщепленных сигналов. Действительно, операция расщепления класса входных сигналов позволяет адаптировать модель к заданному воздействию, в результате чего можно построить более простую модель по сравнению с универсальными формами, например, полиномом Вольтерры. Параметры модели находятся в результате аппроксимации нелинейных операторов устройств с использованием множеств входных и выходных сигналов. В качестве примера построена полиномиальная модель мемристора, динамика тока которого описывается дифференциальным уравнением Бернулли. Выполнено расщепление гармонического входного сигнала в области его определения с помощью линии задержки и построена модель в виде двумерного полинома расщепленных сигналов. Согласно оценкам погрешностей, полученным в равномерной и среднеквадратичной метриках, двумерный полином третьей степени обеспечивает высокую точность моделирования мемристора Бернулли.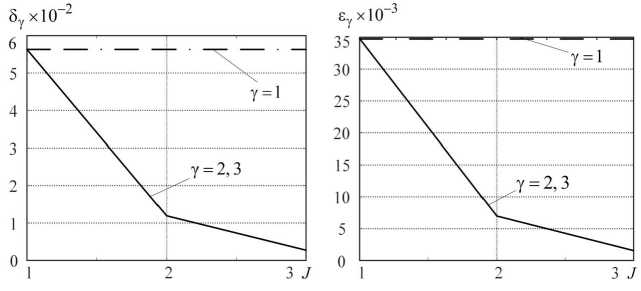
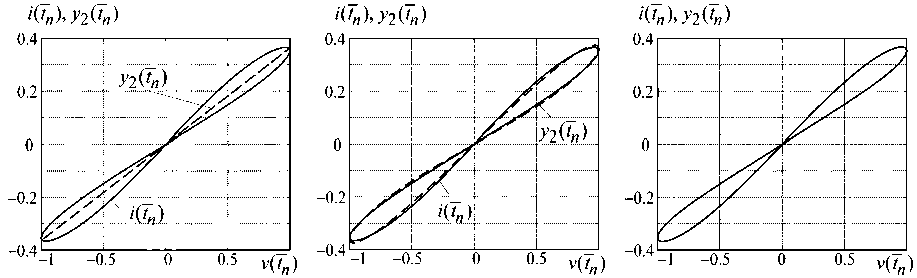
Список литературы Модель мемристоров Бернулли в виде полинома расщепленных сигналов
- Abunahla, H. Memristor Technology: Synthesis and Modeling for Sensing and Security Applications / H. Abunahla, B. Mohammad. - Cham: Springer, 2018.
- Vourkas, I. Memristor-Based Nanoelectronic Computing Circuits and Architectures / I. Vourkas, G.Ch. Sirkoulis. - Cham: Springer, 2016.
- Radwan, A.G. On the Mathematical Modeling of Memristor, Memcapacitor and Meminductor / A.G. Radwan, M.E. Fouda. - Cham: Springer, 2015.
- Solovyeva, E.B. Operator Approach to Nonlinear Compensator Synthesis for Communication Systems / E.B. Solovyeva // International Siberian Conference on Control and Communications (SIBCON), Moscow. - Moscow, 2016. - P. 1-5.
- Solovyeva, E.B. A Split Signal Polynomial as a Model of an Impulse Noise Filter for Speech Signal Recovery / E.B. Solovyeva // Journal of Physics: Conference Series. International Conference on Information Technologies in Business and Industry. - 2017. - V. 803, № 1. - P. 1-6.
- Biolek, Z. Differential Equations of Ideal Memristors / Z. Biolek, D. Biolek, V. Biolkova // Radioengineering. - 2015. - V. 24, № 2. - P. 369-377.
- Chao Ma. Macromodeling of the Memristor Using Piecewise Volterra Series / Chao Ma, Shuguo Xie, Yunfeng Jia, Guanyu Lin // Microelectronics Journal. - 2014. - V. 45, № 3. - P. 325-329.
- Georgiou, P.S. Device Properties of Bernoulli Memristors / P.S. Georgiou, M. Barahona, S.N. Yaliraki, E.M. Drakakis // Proceedings of the IEEE. - 2012. - V. 100, № 6. - P. 1938-1950.


