Модель методической системы профессионально направленной математической подготовки экономистов в вузе

В настоящее время в условиях жесткой конкуренции на рынке труда и модернизации российской системы образования первостепенное значение приобретает профессиональная компетентность специалистов. Мы рассматриваем профессиональную направленность математической подготовки экономистов в вузе как средство формирования их профессиональной компетентности.

Под математической подготовкой экономистов мы понимаем целенаправленный педагогический процесс формирования математической компетентности экономистов, которая позволит им изучать профильные дисциплины, решать задачи в своей профессиональной деятельности, продолжать образование и самообразование в области экономики как на профессиональном, так и на научноисследовательском уровне.

В России высшая школа является в основном профессиональной, поэтому соблюдение принципа профессиональной направленности обучения является важнейшим при подготовке специалиста любого профиля, в том числе экономического. Принцип профессиональной направленности обучения очень значим при решении вопросов содержания, методики и средств обучения, он регулирует в высшем профессиональном образовании соотношение общеобразовательного и специальнопрофессионального, определяет диалектику взаимодействия целостного развития личности и ее профессионального становления. Его особая роль среди других дидактических принципов обучения состоит в том, что он объединяет общей целью все остальные принципы, придает им новый смысл для участников учебного процесса. Мы рассматриваем данный принцип в качестве системообразующего принципа дидактики, направляющего процесс математической подготовки экономистов в вузе.

Под профессиональной направленностью математической подготовки будущих экономистов в вузе мы будем понимать ориентацию математической подготовки в ее целевом, содержательном и процессуальном аспектах на динамическое моделирование профессионального труда экономиста. Таким образом, учебная деятельность студентов будет трансформироваться в профессиональную деятельность специалиста. Это позволит преодолеть главную проблему высшего профессионального образования – обучение профессиональной деятельности средствами качественно иной учебной деятельности.

В качестве ведущей идеи реализации принципа профессиональной направленности была выбрана идея Н.Ф. Талызиной: «…раз-работка обоснованных целей образования не- возможна без выделения основной системы задач, с которыми встретится будущий специалист» [4, с. 7]. Опираясь на эту идею, мы уточнили понятие математической компетентности экономистов как «способность и готовность решать методами математики типовые профессиональные задачи» [1, с. 110]. Если «типовая задача – цель, которая многократно ставится человеком в определенных жизненных ситуациях» [3, с. 5], то типовая профессиональная задача экономиста – это цель, которая многократно ставится в процессе его профессиональной деятельности.

Рассмотрим методическую систему математической подготовки экономистов в вузе, опираясь на понятие методической системы обучения, введенное А.М. Пышкало [2]. В выделенную им структуру методической системы включены пять компонентов: цель, содержание, формы, методы и средства обучения. Смена образовательной парадигмы в настоящее время – от традиционной «ЗУНовской» к компетентностной – предполагает перенос акцента с процесса обучения на его результаты. Это требует существенных изменений во всех компонентах методической системы и добавления нового компонента – результатов обучения (см. рис.).

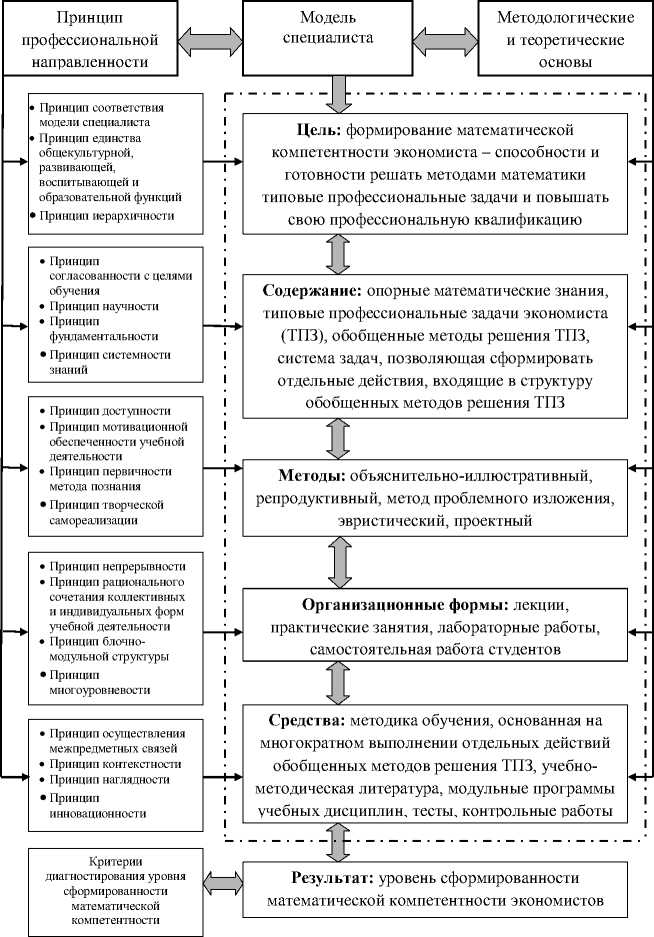
Модель методической системы математической подготовки экономистов в вузе

В качестве цели профессионально направленной математической подготовки будущего экономиста мы рассматриваем формирование его математической компетентности как способности и готовности решать методами математики типовые профессиональные задачи и повышать свою профессиональную квалификацию. Содержание и объем методической системы математической подготовки экономистов регулируются целью обучения и системой дидактических принципов, которые разделены нами на пять групп в соответствии с компонентами методической системы математической подготовки (цели, содержание, методы, формы организации, средства).

Цель математической подготовки экономистов – формирование математической компетентности – подчинена трем принципам.

• 1.    Принцип соответствия модели специалиста . Полное содержание модели специалиста в области экономики определяется конкретными общественно-историческими условиями, особенностями региональной экономики и особенностями профессиональной деятельности. Модель специалиста как совокупность требований общества к специалисту диктует цели его обучения в вузе и его математической подготовки в частности.

• 2.    Принцип единства общекультурной, развивающей, воспитывающей и образовательной функций математической подготовки. Реализация этого принципа предполагает, что при разработке целей применительно к математической подготовке экономистов в вузе необходимо учитывать ее основные функции. Математика является наукой фундаментальной и, кроме образовательного, обладает колоссальными развивающим и воспитывающим потенциалами.

• 3.    Принцип иерархичности. Необходимо регламентировать важный вопрос, связанный с разработкой целей математической подготовки, – переход от ее конечных целей к целям изучения отдельных математических дисциплин и далее – к целям изучения конкретных разделов и тем. Основная цель математической подготовки подразумевает систему подчиненных ей целей – типовых профессиональных задач. Каждая из задач, в свою очередь, подразумевает выделение обобщенного метода ее решения, состоящего из отдельных последовательных действий, имеющих свою цель. Возникает иерархия целей математической подготовки экономистов в вузе.

Ко второй группе относятся принципы, позволяющие отобрать содержание математической подготовки экономистов в вузе.

• 1.    Принцип согласованности с целями обучения. Этим принципом следует руководствоваться при отборе учебного материала, поскольку сама математическая подготовка не рассматривается в качестве цели обучения. Она необходима будущим специалистам, прежде всего, для успешного формирования их профессиональной компетентности, поэтому должна быть согласована с целями всего процесса обучения в вузе и, в частности, с собственными целями.

• 2.    Принцип научности предполагает соответствие содержания учебных математических дисциплин логике построения фундаментальных основ математики. Для реализации этого принципа необходимо обеспечить формирование правильных представлений о научных понятиях, их свойствах и взаимосвязях в принятых научных терминах и на основе диалектического подхода.

• 3.    Принцип фундаментальности. Фундаментальность математической подготовки предполагает выделение набора основных понятий и методов, служащих основой для изучения других дисциплин.

• 4.    Принцип системности знаний . Соответствие требованию системности означает, что математическая подготовка не превратится в совокупность отрывочных сведений слабо взаимосвязанных математических дисциплин, требующихся для дальнейшей подготовки специалиста, но обладает полнотой, взаимообусловленностью и последовательностью всех составляющих ее частей.

Третью группу составляют принципы, позволяющие определиться с формами организации математической подготовки экономистов в вузе.

• 1.    Принцип непрерывности. Следует обеспечить непрерывность математического образования студентов в течение всего времени их обучения в вузе. Математическая подготовка экономистов не ограничивается изучением базовых математических дисциплин и информатики, а непрерывно продолжается в последующем процессе специализации.

• 2.    Принцип рационального сочетания коллективных и индивидуальных форм учебной деятельности. С одной стороны, обучение в вузе предполагает организацию индивидуальной самостоятельной работы, творческого поиска знаний, с другой – развитие коммуникативных навыков, коллективный поиск решения в процессе проектной деятельности, безусловно, способствуют активизации процесса обучения. Сочетание коллективного и индивидуального в обучении создает необходимую

• 3.    Принцип блочно-модульной структуры подразумевает организацию математической подготовки на основе блочно-модульного представления учебной информации. Введение кредитно-модульной системы обучения в вузах позволяет обеспечить возможность выбора студентом индивидуальной образовательной траектории, усиливая роль и ответственность студента в организации учебного процесса.

• 4.    Принцип многоуровневости. В соответствии с этим принципом математическая подготовка экономистов в вузе должна быть организована с учетом как двух уровней современной системы высшего российского образования, так и уровней формирования математической компетентности специалистов.

среду для развития студента и его профессионального становления.

Четвертая группа принципов определяет методы обучения математике.

• 1.    Принцип доступности. Имеется в виду не учет возрастных или индивидуальных особенностей обучаемых, а соответствие методов обучения уровню математической и профессиональной грамотности студентов на момент обучения, поскольку используемые в процессе математической подготовки методы дисциплин математического и профессионального циклов должны быть доступны обучающимся.

• 2.    Принцип мотивационной обеспеченности учебной деятельности. Преподаватель должен использовать такие методы обучения, которые стимулируют студентов к учебной деятельности, помогают им осознать значение изучаемого математического материала для будущей профессиональной деятельности.

• 3.    Принцип первичности метода познания. Методы изучения той или иной дисциплины должны отражать методы познания соответствующей науки. В математической науке используются такие методы познания, как дедукция, индукция, анализ, синтез, моделирование, наблюдение, измерение, сравнение, аналогия, обобщение, конкретизация. Эти методы должны определять и основные методы изучения математики.

• 4.    Принцип творческой самореализации. Следует добиваться оптимальности соотношения учебной деятельности под руководством преподавателя и сознательной творческой самостоятельной деятельности студентов. Реализация этого принципа особенно актуальна сегодня, после утверждения в системе высшего профессионального образования ФГОС третьего поколения, в соответствии с которыми половина учебного вре-

• мени отводится на самостоятельную работу студентов.

Наконец, пятую группу составляют принципы, регулирующие вопрос выбора средств обучения в процессе математической подготовки экономистов.

• 1.    Принцип контекстности. Ориентация математического образования на профессиональный контекст позволяет рассматривать средства математической подготовки как подсистему средств профессионального образования и выделять профессионально значимые типы задач, в процессе решения которых будущие экономисты смогут овладеть видами деятельности, адекватными их будущей профессии.

• 2.    Принцип осуществления межпредметных связей. Связь математики и профильных дисциплин рассматривается в качестве средства математической подготовки экономистов. Применение знаний из других дисциплин свидетельствует о наличии этих знаний, прочности их усвоения, о сформированности умений и навыков обращения к знаниям других предметных областей, что позволит преодолеть противоречие между целостностью профессиональной деятельности и фрагментарностью ее освоения в рамках отдельных учебных дисциплин.

• 3.    Принцип наглядности. Являясь классическим в дидактике, данный принцип предполагает использование чувственно-образных элементов в обучении.

• 4.    Принцип инновационности. Внедрение в учебный процесс технологичных средств обучения (электронных учебников, обучающих программ, математических пакетов программ и др.) позволяет не только повысить качество преподавания, но и сформировать культуру интеллектуального труда студентов и их самостоятельность; усилить активность обучаемых; изменить ценностные ориентации и мотивационные установки как студентов, так и преподавателей.

Результатом обучения является уровень сформированности математической компетентности будущего экономиста, который диагностируется с помощью разработанной системы критериев.