Модель оптимизации усредненной скорости потока жидкости в трубе

В последнее время на производственных предприятиях становится все более актуальной задача высокоточного учета газа. Для решения таких задач применяется расходомер-счетчик газа (или просто расходомер), который предназначен для измерения объемного расхода газа при рабочих условиях, для вычисления массового расхода, массы и теплоты сгорания газов. Такое устройство основано на методе измерения разности между временем прохождения ультразвуковых импульсов по потоку и против потока газа и предназначено для технологического контроля и для использования в системах коммерческого учета. Поскольку одним из критериев работы прибора является точность вычисления расчетов, ставится вопрос о получении точной оценки средней скорости турбулетного потока жидкости, проходящей вдоль трубопровода.

Рассмотрим схему двухлучевого ультразвукового расходомера, изображенную на рис. 1, 2. Для каждого акустического маршрута ультразвуковые датчики (из B в A) посылают и обнаруживают короткий звуковой импульс с наклонным направлением, где θ i – угол между акустическим маршрутом и стенкой трубы. Здесь i – номер акустического пути, который имеет боковое расположение относительно осевой линии на расстоянии r i , а d i – хордовое расстояние между двумя датчиками. Восходящий сигнал является задерживающим, в то время как нисходящий сигнал является ускоряющим при движении жидкости по трубопроводу.

Точная оценка средней скорости потока вдоль поперечного сечения трубы

n vM =   ωivMi i=1

описывается с помощью линейной комбинации весов (каждый из которых находится с помощью оптимизационной задачи для абсолютной погрешности невязки || V — v_M||).

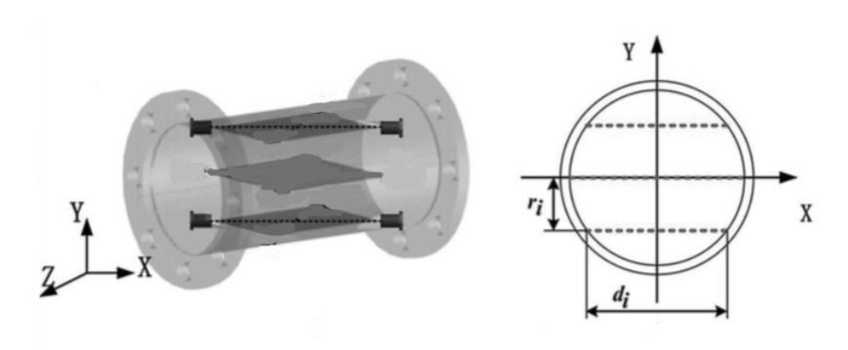
Рис. 1 . Модель двухлучевого расходомера

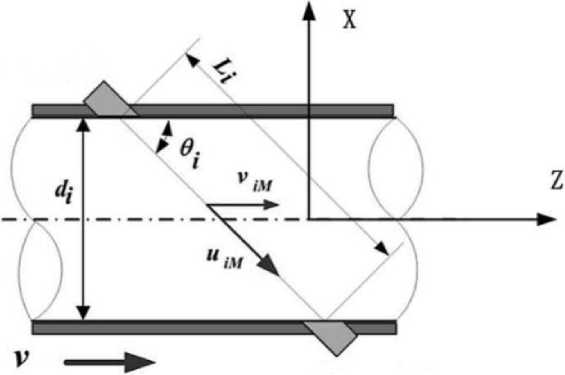
Рис. 2 . Сечение профиля скорости

Здесь v _Mi - измеренная скорость потока на i-ом акустическом пути, i = 1,n, V -теоретическая скорость потока жидкости в трубе. При измерении потока одним из главных вычислительных параметров является абсолютная погрешность измерения. Таким образом, в качестве основной производственной задачи рассматривается минимизация невязки 5 = || V — v _M || и решение задачи нелинейного программирования с условиями типа неравенств:

n

V Mopt = argmin || V — vm || = argmin || V — ^ W i V Mi || , и}            w     i =i

w i <  1, u i >  0, i = 1, n.

Как предложено в работе [1], для нахождения весовых коэффициентов u i , i = 1,n, необходимо провести m экспериментальных измерений и получить набор точек (V j ,v _M 1j , • • • ,v _Mnj ), j = 1,m, для нескольких поперечных сечений и решить задачу условной оптимизации (1). Здесь V j – усредненная скорость потока жидкости, а v _Mij – усредненная скорость ультразвукового потока на j -м измерении. Учитывая, что для n -лучевого ультразвукового расходомера V j вносит вклад в полную скорость потока

• V, а значение w i лежит в пределах [0,1], достаточно найти вектор невязки

n

^ j — v Mj

-

V j ^— 52 ^W ij v Mij

- V j

n <  m,j — 1, • • • , m.

i =1

Тогда задача условной оптимизации (1) может быть сведена к задаче минимизации функционала абсолютной погрешности

m

S(w) — J>Mj - V j ) 2

i =1

mn

—s's

^ω ij ^v M ij

2 m

— Ej j=1

Таким образом, основная задача сводится к определению такого вектора весов ш * — (ш * , w * , • • • , ш П ), при котором функционал (2) принимал бы минимальное значение

V Mopt — argmin S (ш * ). М}

• 1.    Аналитическое значение усредненной скорости

В дальнейшем для простоты расчетов будем рассматривать упрощенную модель усредненной скорости потока жидкости в трубе для двухлучевого ультразвукового расходомера (рис. 3), тогда

S(ш) — (ш 1 • V M 11 + W 2 • V M 21

- V 1 ) .

По условию задачи имеем две плоскости П ₁ и П ₂ , симметрично расположенные относительно осевой плоскости D (рис. 3). В плоскости П ₁ расположен ультразвуковой поток AB, а в плоскости П ₂ – ультразвуковой поток A ₁ B ₁ . Кроме того, в дальнейшем будем считать прямые AB и A 1 B 1 параллельными и составляющими угол θ i со стенкой трубы. Возьмем расстояние между плоскостями (П 1 и D, П 2 и D соответственно) равное ± r 1 и найдем явный вид целевой функции.

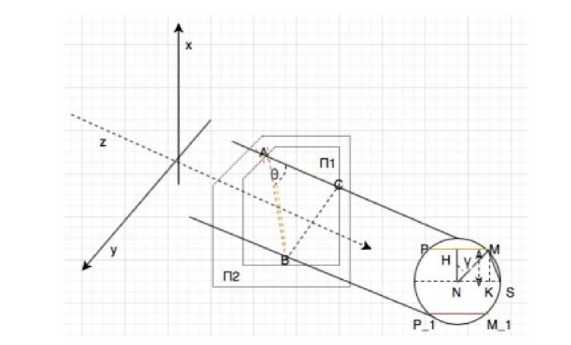
Рис. 3 . Вид сверху

Используя метод двумерной интерполяции по набору точек { (x i , y i ) } , построим поверхность z(x,y ) так, чтобы z(x i ,y i ) = v i на плоскости поперечного сечения трубы, где { v i } – заданный набор усредненных мгновенных скоростей на плоскости поперечного сечения. (Получим эпюру скорости V(x, у), которая в рамках исходной задачи не зависит от z , т.е. постоянна вдоль трубы.) Под усредненной скоростью потока жидкости вдоль трубы будем понимать

V=

1ГI v • n

S _Ω Ω

dS,

где Q - плоскость поперечного сечения трубы, n - единичная нормаль к Q, v = (0, 0, z(x, у)).

S _Ω – площадь поперечного сечения,

Для нахождения усредненной скорости v Mi 1 на ультразвуковом маршруте прежде всего разберемся с исходными данными. По условию задачи известен угол θ между лучом AB и стенкой трубы; (оптимизационное) расстояние r ₁ между осевой плоскостью D и плоскостью П ₁ ; внутренний диаметр трубы d (соответственно, радиус R). Под усредненной скоростью вдоль ультразвукового маршрута v _Mi1 в прямоугольной системе координат примем криволинейный интеграл первого рода вдоль гладкой кривой L

V Mii = щ I z(x,f (x))dS, L

где

x 1

| L | = / V¹ + (f x (x)) 2 dx, x 0 ≤ x 1 .

x 0

Скорость v Mi 2 вычисляется аналогично (5). Уравнение хорды MP в плоскости поперечного сечения трубы примет вид

{ — R sin(Y) <  x <  R sin(Y), Y = arccos —,

У = r i ,

тогда

V Mii = j^ У z(x,r i )dS, L

где длина кривой

x P

^{| L |} = У V¹ + ⁽ r i ) X dx.

x M

Таким образом, получили иную интерпретации количественных характеристик по сравнению с результатами работы [1].

2. Численное нахождение усредненной скорости

Одним из самых распространенных языков программирования прикладных пакетов получения и анализа данных является язык программирования Python. Для

вычисления теоретической скорости турбулентного потока жидкости в ходе выполнения работы было рассмотрено следующее распределение [3]

V=V o о - 9^т -

где V ₀ – скорость на оси трубы, r – расстояние между определенной точкой и осью в плоскости поперечного сечения, параметр l связан с числом Рейнольдса (Re >  20000) и подбирается в результате экспериментальных данных. Стандартный интерполяционный двумерный метод для построения эпюры скорости на основе радиальных базисных функций показал неточность вычислений. А именно, графики уравнений хорд на эпюру скорости z(x, у ) и скорости в плоскости поперечного сечения, изображенные на рис. 4, 5, выявили нарушение гладкости полученной функции вблизи стенок трубы. Это объясняется тем, что метод interpolate.Rbf , описанный в библиотеках

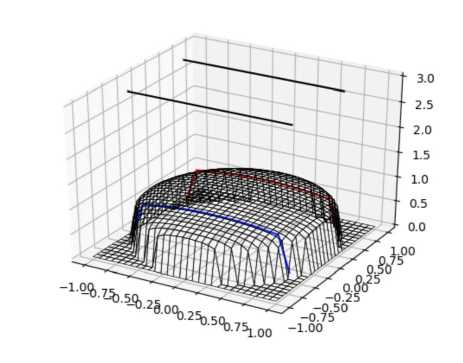
Рис. 4 . Эпюра скорости z(x, у )

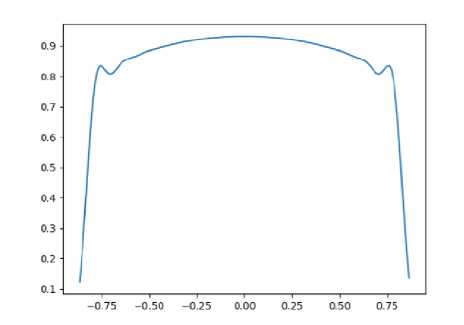
Рис. 5 . Сечение профиля скорости

Python, не подходит в тех случаях, когда на поверхности эпюры скорости происходит резкое изменение значений скорости вблизи стенок трубы, что проиллюстрировано на рис. 5.

Для получения интерполирующей поверхности эпюры скорости z(p, ^) в дальнейшем будем применять метод CloughTocher2DInterpolator , который основан на триангуляции области сечения трубы по Делону и построении кубического сплайна с использованием треугольников Сие – Клафа – Точера. Отметим, что в качестве аппрок-симанта функции f на треугольнике T используется гладкая кусочно-полимиальная функция P 3 , которая на каждом T i , 1 <  i <  3 является многочленом третьей степени (по совокупности переменных)

3- i

P3,i = ^Cij Ху j- j=0

для задания которого требуется 10 переменных. Для определения P ₃ , таким образом, требуется 30 условий, среди которых: условие непрерывности функции и ее производных первого порядка по двум несовпадающим направлениям в центре треугольника; условие непрерывности на значения функции f и первых производных f _x и f _y в каждой вершине, нормальных производных в средней точке трех ребер в треугольнике.

Поскольку все элементы на рассматриваемой триангуляции являются треугольниками Сие – Клафа – Точера, результирующая функция, построенная на плоскости поперечного сечения трубы, будет непрерывно-дифференцируемой (более подробное описание метода конечных элементов см., например, в [2, 5]).

Основываясь на алгоритме, описанном выше, перепишем формулу для получения усредненной скорости по ультразвуковому маршруту в полярной системе координат:

^v Mi 1

ϕ 1

iLpi /*4

ϕ 0

² r ₁ sin ² (^)

r i COS 2 (to) ,

⁺ sin ⁴ (p) d^’

где                               _ϕ

I LJ = Л I     +       ^                (11)

J у Sin ² (^)     Sin ⁴ (^)

ϕ 0

у - полярный угол в новой системе координат, р(^) — радиус-вектор. Запишем полученные результаты количественных характеристик в полярной системе координат для целевой функции (3). Здесь для R = 1,n = 10, V 0 = 1,r i = 0,5 имеем V 1 = 0, 865772, vm_n = 0, 870870, vm 21 = 0, 870870.

Таким образом, имеем следующий функционал:

S M = S (Ш 1 , U i ) = 4 • 0,870870 + ш 2 • 0,870870 - 0,865772^ ,

для которого рассмотрим задачу нелинейного программирования с условиями типа неравенства

S(ш ) ^ min,

Ш 1 <   1, Ш 2 <   1, Ш 1 >  0, Ш 2 >   0.

Для наглядности построим график целевой функции (рис. 6) в необходимой области и найдем экстремальные точки (ш) = (ш1,ш2).

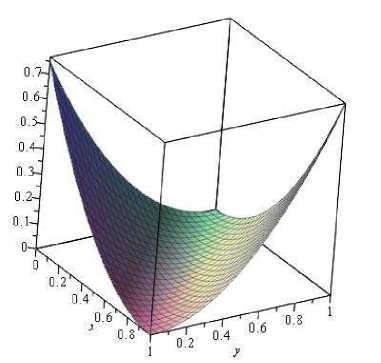
Рис. 6 . Целевая функция S (ш), описанная формулой (12)

Имеем

S (w ) =

(0, 870870) 2 • ( (w 1 + ш ₂ ) - с )

где с =

0,865772

0,870870

= 0,994146.

Поскольку сечением построенной поверхности является парабола с ветвями, направленными вверх, понятно, что минимум данной функции представляет множество точек, являющихся вершинами параболы. Таким образом, используя геометрическую интерпретацию поведения функции, нетрудно найти набор экстремальных точек { w i } . В силу того, что 0 <  с <  2, целевая функция S(ш ) достигает локального минимума, совпадающего (в данном случае) с глобальным, если весовые коэффициенты связаны следующим равенством: w ₀ + w 1 = с.

Заключение

Получено решение на примере двухлучевого ультразвукового расходомера для модели оптимизации, которая представляет точную оценку средней скорости тур-булетного потока жидкости, проходящей вдоль трубопровода. Построен метод нахождения количественных характеристик без учета измерения времени прохождения восходящих (нисходящих) ультразвуковых потоков по акустическим маршрутам. Поскольку искомая модель представляет задачу условного экстремума (13) с ограничениями типа неравенства, в ходе выполнения работы использовалось необходимое условие теоремы Каруша – Куна – Таккера для нахождения точек, подозрительных на экстремальные.