Модель отклонения трактора от прямолинейного движения под действием внешних нецентральных сил

В настоящее время широкий интерес вызывают различного рода беспилотные проекты. Основной проблемой проектирования таких средств передвижения является разработка автоматизированной системы управления машиной. И если в области создания беспилотных автомобилей в мире наметился определенный прогресс [1–3], то относительно тракторной и строительнодорожной техники эти вопросы находятся еще в самом зародыше.

Объясняется это отставание более сложным внешним воздействием на базовую машину в составе тракторного агрегата. В отличие от автомобиля любой тракторный агрегат подвержен внешнему воздействию не только со стороны движителя, но и со стороны рабочего органа. Подчас именно внешние силы со стороны рабочего органа определяют характер движения транспортного средства.

Если внешняя сила не проходит через центр тяжести, ее называют внецентровой. Она, как правило, создает дополнительный разворачивающий момент, изменяющий управляемое движение машины.

Примеры действия внецентренной внешней силы

Характерным примером может служить движение сельскохозяйственного тракторного агрегата [4, 5]. Например, при работе трактора с консольной косилкой (рис. 1) сила сопротивления на рабочем органе приводит к отклонению машины от прямолинейного курса. Аналогичная ситуация наблюдается при вспашке земли (рис. 2). Конструкция лемешного плуга такова, что возникающие на нем силы сопротивления, направленные по нормали к отвальной поверхности, созда- ют разворачивающий момент. Для сохранения прямолинейного движения водителю приходится постоянно подправлять машину [6, 7], что приводит к повышенной его утомляемости.

Рис. 1. Трактор с консольной косилкой

Рис. 2. Трактор с лемешным плугом на вспашке

Боковые нагрузки на базовую машину встречаются и при работе строительно-дорожной техники. Наиболее характерной машиной в этом случае является автогрейдер [8, 9]. Эта машина с помощью дополнительной навески позволяет обрабатывать дорожные обочины (рис. 3). При управляющем воздействии со стороны водителя, соответствующем прямолинейному движению, машина часто теряет курсовую устойчивость за счет внешнего воздействия [10].

Рис. 3. Работа автогрейдера при чистке и укладке дорожных обочин

Отклонение трактора от управляемого прямолинейного движения возможно и при работе бульдозера. Так, в случае перекоса отвала (рис. 4) или работе с поворотным отвалом (рис. 5) вся внешняя нагрузка воспринимается одним краем, что тоже приводит к возникновению внешнего разворачивающего момента, влияющего на характер движения трактора [11, 12].

Рис. 5. Работа снегоочистительного трактора с поворотным отвалом

Рис. 4. Работа бульдозерного агрегата с перекосом отвала

Отклонение трактора от управляемого прямолинейного движения получило название пассивного увода [13, 14]. Этот вид движения на сегодняшний день мало изучен, поскольку криво-

Жаков А.О., Трояновская И.П.

линейное движение в основном исследуется на примерах активного поворота [15]. При создании различных систем помощи водителю воздействие внецентровых внешних сил на движение машины должно быть обязательно учтено.

Цель исследования

При проектировании беспилотных транспортных средств на первое место выходит задача управления. Однако ее решение невозможно без разработки математической модели движения с учетом всех внешних факторов. В связи с этим целью исследования является построение математической модели пассивного увода тракторного агрегата при воздействии внешних внецентрен-ных сил.

• 1.    Математическая модель

Пассивный увод представляет собой совокупность двух типов движения:

– управляемого (при воздействии водителя) прямолинейного движения;

– неуправляемого (под действием внешних сил) пассивного сдвига.

Математическая модель увода представляет собой квазистатическую модель, состоящую из модели криволинейного движения и модели силового равновесия.

• 1.1.    Уравнения движения

Все тракторные агрегаты являются машинами циклического типа, технологический цикл ко- торых включает рабочий и транспортный режим движения. Внешние нагрузки со стороны рабо- чего органа действуют в рабочем режиме, когда скорость движения трактора невысока и, как правило, постоянна V = const. Это позволяет пренебречь ускорениями.

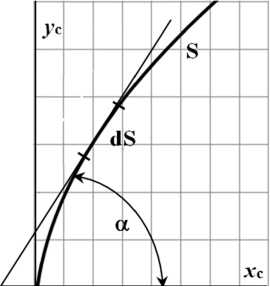
Рис. 6. Связь криволинейной координаты S с декартовыми координатами х с и у с

Построим модель отклонения тракторного агрегата от прямолинейного движения под действием внешних сил. Для этого преобразуем криволинейную координату S естественной системы подвижного трехгранника в декартовы координаты хс, ус на основе криволинейного интеграла первого рода (рис. 6).

При начальных нулевых координатах уравнения движения имеют вид:

cosadS sinadS

}

^х с = 4

Ус = J$ где хс, ус - текущие координаты центра тяжести трактора;

dS – дифференциал криволинейной координаты в точке α – угол касательной к кривой в точке с осью x.

Запишем дугу S через радиус кривизны ρ и угол касательной α соотношением dS = pda.                                                                               (2)

Учитывая, что dS = VdT и a = / (V / p)di , формулы (1) приобретают вид [16]: Т          t V

^ с = J o Vcos^J₀ - dz)dt

Ус = JoTvsin (Jo V dT)dt где t = 0.. .Т - время; V - скорость движения транспортного средства.

Таким образом, для построения траектории движения необходимо знать радиус кривизны ρ в каждый момент времени. Его значение определяется действием внешних сил. Для этого составим силовую модель.

• 1.2.    Силовое равновесие

При пассивном уводе произвольного тракторного агрегата на него действуют силы со стороны движителя F и со стороны рабочего органа P. В каждый момент времени система действую- щих на трактор сил уравновешена, что позволяет записать уравнения равновесия:

F_x + Р_х = 0,

I

Fy + Ру = 0, Мс + МС(Р) = 0, где Fx, Fy - сумма поперечных и продольных составляющих сил со стороны движителя, Mc - суммарный момент сопротивления в контакте движителя с грунтом; Px, Py,Mc(P) - суммарные проекции на декартовы оси и момент от суммы внешних сил со стороны рабочего органа.

Рассмотрим силовое равновесие на примере сельскохозяйственного трактора с лемешным плугом (рис. 7).

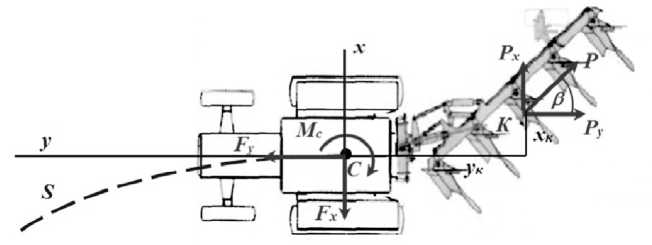
Рис. 7. Схема сил, действующих на тракторный агрегат при пахоте

Свяжем систему координат с центром С тяжести трактора. Приведем все силы на плуге к результирующей Р , приложенной в точке К , с координатами у_кх_к. Тогда проекции внешней силы на плуге на декартовы оси будут равны:

P_x = Psine, P_y = —Pcose .                                                         (5)

Момент внешней силы относительно центра тяжести трактора в общем виде имеет вид:

M c (P) = P_xy_k - P y X_k .                                                                   (6)

• 1.3.    Силы в контакте движителя с грунтом

Управляемое водителем движение является прямолинейным и характеризуется отсутствием относительного движения между опорами движителя (колесами или гусеницами). Это позволяет рассмотреть контакт с грунтом как единую площадку с разрывными вдоль и поперек пределами.

В силу того, что силы в контакте движителя с грунтом по своей природе являются силами трения [17], воспользуемся математической теорией трения. Силовые факторы при плоском скольжении движителя относительно грунта являются функциями координат мгновенного центра скольжения и имеют вид [18]:

F = —q ff ц /   ^y. ^ф ^— d y d o ,

^X         W 7(У- Ф )² + (х- у )^{2  1}

F = q ff Ц ~^==== d y d o , ^У       ^  7(У-Ф)² + (^Х-Т)²

M = qH ^_Y ^ V (У — Ф ) ² + ⁽х — Y ) ² d y d p , M c = F y X — F x y — M       .

где p - коэффициент сцепления движителя с грунтом; q - нормальное давление в контакте;

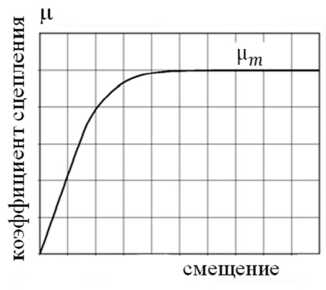
Рис. 8. Качественная зависимость коэффициента сцепления от смещения относительно грунта

x, y – координаты мгновенного центра скольжения при плос-

ком сдвиге; у, ф - текущие координаты точек контакта.

Наличие несимметричного профиля протектора шин или

грунтозацепов на гусеницах приводят к анизотропии взаимодействия, которая может быть учтена с помощью различных

коэффициентов сцепления в продольном р_у и поперечном р_х

направлении. В этом случае момент сопротивления в контакте

имеет вид [19]:

M = qH

ϕγ

Цх(у-ф)2+у(х-у)2

V(y-V)2 + (x-y)2

^у^ф.

Упругие свойства грунта и шины в контакте учтем по-

средством переменного коэффициента сцепления µ (рис. 8), зависящего от смещения [20–22].

Жаков А.О., Трояновская И.П.

Смещение движителя относительно грунта напрямую зависит от радиуса р кривизны траектории. Это позволяет записать переменный коэффициент сцепления в виде:

н = мЧ* ^.                                     (9)

где ц _т - максимальный коэффициент сцепления (при 100%-ном буксовании); th - функция гиперболического тангенса; λ – эмпирический коэффициент, характеризующий упругие свойства в контакте (грунта или шины).

В результате модель силового равновесия (4) с учетом всех преобразований (5)–(9) принима- ет вид:

^^^^^в

гг ^hHifc^ ^q ^^Y 7(У-Ф)^{2 +} (^Х-У)

, 2

dyd^ + Рзипв = 0,

^ymth[ ХЙ^] (^-Y)

^ Д„ 7( _У -ф)2 + (х-у)2 ^^Ф - ^{РС05 в = 0},

^™th[ XS](x"Y)

^ _V(y__w) 2 +(x__Y) 2 ^^{Ф +}

^^thl xs](y-v)   л

• + yq II —,   ^  —- аунф —

V^Y V⁽y~V⁾² + ^(x~Y⁾²

^^^^^в

• ^^^{th| X}S^](y-V^{)2 +} ^ym^th[ ^^^](^"^Y)2 q| ----- /        „ —----dv^v +

• 2.    Результаты исследования (построение траектории)

v^y            Vcy-v^^+cX^Y)²

+y_kPsvne + х_кРсозв = 0.

Из уравнений (10) видно, что для каждой внешней сдвигающей силы со стороны рабочего органа (с модулем Р , углом наклона в и координатами точки приложения y_fc , %_fc ) можно однозначно определить координаты х, у мгновенного центра скольжения и радиус кривизны траектории ρ базового трактора. Далее на основе уравнений движения (3) строится траектория движения с учетом внешних сдвигающих сил со стороны рабочего органа (рис. 9).

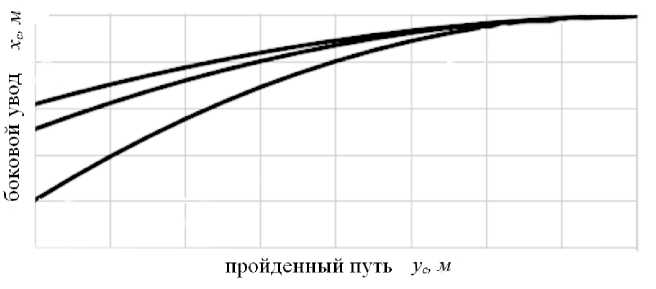
Рис. 9. Траектория увода сельскохозяйственного трактора при действии внешней нагрузки на плуге

Выводы

Тракторные агрегаты отличаются от транспортных средств тем, что контактируют с грунтом не только посредством движителя, но и рабочим органом. Внешние усилия со стороны рабочего органа порой оказывают существенное влияние на движение базовой машины. Анализ работы различных тракторных агрегатов позволил выявить явление пассивного увода – отклонения трактора от управляемого движения водителя за счет действия внецентровых внешних сил. Этот тип движения на сегодняшний день оказался мало исследованным.

Пассивный увод представляет собой совокупность прямолинейного управляемого движения и неуправляемого криволинейного сдвига под действием внешних сил. В статье разработана ма- тематическая модель пассивного увода трактора, состоящая из уравнений движения и системы силового равновесия.

Силовое взаимодействие основано на математической теории трения и позволяет учесть анизотропию в контакте движителя с грунтом, а также упругие свойства грунта и шины.

Квазистатическая модель увода позволяет:

• –    построить реальную траекторию движения с учетом внешних факторов;

• –    определить боковое отклонение трактора от прямолинейного движения в любом месте пути;

• –    оценить влияние значения внешней силы, ее направления и точки приложения на траекторию движения;

• –    исследовать влияние характеристик грунта и скорости движения на параметры движения.