Модель перемежаемости глобальных минимумов и максимумов в солнечном динамо

Важной характеристикой циклических процессов солнечной активности являются локальные экстре мумы отдельных циклов . В конце XIX в . Вольф определил моменты экстремумов и амплитуды 11- лет них циклов с 1610 г ., т . е . со времен первых те лескопических наблюдений , включая Маундеров - ский минимум . На сегодняшний день не вызывает сомнений существование длительных минимумов в пятнообразовательной деятельности Солнца – так называемых « глобальных минимумов » солнечной активности , для которых характерное число Вольфа в максимуме 11- летнего цикла не превышает 80 [ Ви - тинский и др ., 1986]. Менее распространенный термин – « глобальные максимумы » солнечной актив ности ; они характеризуются последовательностью нормальных по мощности 11- летних циклов активнос ти в максимуме цикла с числом Вольфа больше 80. Глобальные минимумы ( максимумы ), по всей веро ятности , присутствуют и на подобных Солнцу звез дах [Saar, Baliunas, 1992].

Выделение глобальных минимумов ( максиму мов ) практически всегда основано на исторических или косвенных сведениях о числе солнечных пятен . Наиболее длинный исторический ряд данных о пятенной активности Солнца – ряд Шове [Schove, 1955], непрерывная часть которого охватывает око ло 1700 лет . Этот ряд создан на основе истори ческих письменных сведений о наблюдениях раз личных явлений природы . Ряды косвенных данных о солнечной активности более длинные . Рекон струируют такие ряды по скорости образования и концентрациям « космогенных » изотопов (¹⁴C и ¹⁰B) в разных земных средах ( древесные кольца , сталак титы и др .) [Nagaya, et al., 2008; Solanki, et al., 2004; Eddy, 1977].

Впервые Эдди [Eddy, 1977] по реконструированному ряду данных солнечной активности выделил шесть глобальных минимумов в течение 5000 лет. Следует отметить, что ближайшие к современной эпохе пять глобальных минимумов солнечной активности названы именами Дальтона, Маундера, Шперера, Вольфа и Оорта. По таким характеристикам, как глубина и продолжительность, выделено два типа глобальных минимумов: более глубокие, но короткие (Маундеровского типа) и более продолжительные (тип Шперера). В работе [Usoskin, et al., 2007] по реконструированному ряду чисел солнечных пятен с временным разрешением 10 лет (восстановленный по данным концентрации радиоуглерода 14C [Solanki, et al., 2004]) выделено 27 глобальных минимумов в солнечной магнитной активности в интервале времени 11400 лет.

Приведем основные характеристики квазиодиннад-цатилетних циклов солнечной активности в эпоху глобальных минимумов. Наиболее полно изучен Маун-деровский минимум солнечной активности по сравнению с другими глобальными минимумами, так как для исследования этой эпохи доступны не только косвенные данные, но и исторические данные, включая первые телескопические наблюдения. Принимая во внимание, что мы исследуем поведение одной динамической системы во времени, описанные закономерности будут распространяться на все известные глобальные минимумы солнечной активности. Установлено, что 11-летние циклы в течение Маундеровского минимума не прекращались, а лишь сильно уменьшились по амплитуде (например [Nagovitsyn, 2007; Nesme-Ribes, et al., 1994]). В работе [Nagovitsyn, 2007] приведены аргументы в пользу того, что смена знака магнитного поля 11-летних циклов в эту эпоху происходила в соответствии с законом Хейла (22-летний цикл). Что касается продолжительности 11-летних циклов, по результатам разных исследований она составляет от 9 лет до 14 лет. Сравнительный анализ восстановленных диаграмм бабочек по историческим данным в период 1620– 1719 гг., перекрывающий Маундеровский минимум, и диаграмм современной эпохи выявил три типа 11-летних циклов: «нормальные» солнечные циклы (отно- сятся к эпохам глобальных максимумов), циклы GM (11-летние циклы глобальных минимумов) и «слабые» циклы (циклы переходных эпох) [Nesme-Ribes, et al., 1994]. Циклы GM характеризуются продолжительностью 9-10 лет, малым числом солнечных пятен и значительной северо-южной асимметрией. Исследование реконструированных временных рядов солнечной активности с годовым временным разрешением в период 1413–1745 гг., перекрывающий глобальные минимумы Шперера (1416–1534 гг.) и Маундера (1645–1715 гг.), показало, что продолжительность 11-летних циклов составляет около 14 лет в эпохи глобальных минимумов и около 11-лет в эпохи глобальных максимумов [Nagaya, et al., 2008].

Что касается природы глобальных минимумов , одна из гипотез – интерференция циклов различной длительности ( например векового и 600- или 400 летнего ) [ Витинский и др ., 1986]. Эпохи глобальных минимумов и максимумов качественно объясняются суперпозициями экстремумов 205-, 360- и 1200 летних циклов [Komitov, et al., 2003]. Указанные компоненты выделены по восстановленному вре менному ряду данных солнечной активности Шове (1700 лет ). На более длинном (11400 лет ) реконстру ированном ряде чисел солнечных пятен с времен ным разрешением 10 лет выявлены 100-, 200- и 2300- летние вариации в возникновении глобальных минимумов , которые наступают , когда фазы мини мумов указанных компонент совпадают [Mord-vinov, Kramynin, 2010]. Однако физическая приро да 100-, 200- и 2300-, а также 205-, 360- и 1200- летних циклов остается неясной . Предлагаемые модели также не описывают различную протяженность и глубину ( высоту ) глобальных минимумов ( макси мумов ).

Другое объяснение природы глобальных мини мумов и максимумов заключается в том , что дина мическая система , моделирующая циклические свой ства процесса пятнообразования , не прекращает сво его функционирования , но спонтанно скачком пере ключается на другой режим и также возвращается обратно . Выделяются три класса моделей динамо , описывающих явление перемежаемости « нормаль ных » циклов активности с глобальными миниму мами . Во - первых , нелинейные модели динамо могут проявлять хаотическое поведение [Ruzmaikin, 1983; Ruzmaikin, 1990; Weiss, et al., 1984]. Такое пове дение , однако , обнаруживается лишь в моделях с малым числом степеней свободы , например , когда удерживаются лишь первые члены разложения полей в ряд по базисным функциям . Хаотические решения полных уравнений динамо до сих пор не найдены . Во - вторых , в нелинейном динамо воз можна длиннопериодическая модуляция амплитуды магнитных циклов . Модуляция может возникать в результате биений между различными модами динамо с близкими частотами [Brandenburg, et al., 1990; Sokoloff, 1994], а также из - за взаимодействия магнитного поля с неоднородным вращением [Kitchatinov, et al., 1994a;

Küker, et al., 1999]. Трудность такого подхода связана с тем, что глобальные минимумы происходят нерегулярно, т. е. не представляют периодического явления [Usoskin, et al., 2007]. Длиннопериодическая модуляция скорее имеет отношение к вековому циклу активности, чем к глобальным минимумам [Кичатинов, Пипин, 1998; Kitchatinov, et al., 1999]. В-третьих, коэффициенты переноса в уравнениях динамо, такие как турбулентная диффузия η или коэффициент α, содержат случайные флуктуации. Это приводит к нерегулярным изменениям амплитуды магнитных циклов [Hoyng, 1988; Choudhuri, 1992]. Данный подход также имеет свои трудности. Для воспроизведения глобальных минимумов требуются слишком большие флуктуации, сравнимые и даже превышающие по величине средние величины. Наконец, имеются комбинированные модели глобальных минимумов.

В модели динамо данной работы учтена зави симость диффузии от магнитного поля . Выясняется , что такая зависимость приводит к явлению гис терезиса , когда в некотором интервале значений ди намо - числа вблизи критического имеется два возможных режима : магнитные циклы постоянной и относительно большой амплитуды и затухающие колебания малой амплитуды . Относительно малые флуктуации α ( δα∼ 0.1 α ) способны вызывать пере ходы между этими режимами . Обнаруженный гис терезис в динамо , когда при прочих равных усло виях возможны магнитные циклы с существенно различающимися амплитудами , может иметь отно шение к наблюдаемым глобальным минимумам .

Описание модели

Основным параметром моделей солнечного и звездного динамо является динамо - число

α Ω R ³

D =       ,

η ²

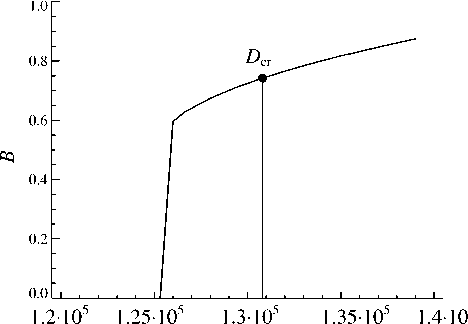
где Ω – угловая скорость звезды , R – ее радиус , η – эффективная магнитная диффузия , параметр α определяет интенсивность генерации поля цикло нической конвекцией [Parker, 1955; Вайнштейн и др ., 1980]. Имеется критическая величина динамо числа D _cr для генерации поля . При величине D меньше критической магнитное поле затухает , а при D > D _cr возрастает со временем . Рост останав ливается при достаточно больших напряженностях поля из - за обратного влияния поля на генерирующие его течения , т . е . из - за нелинейных эффектов .

В подавляющем большинстве нелинейных моде лей динамо учитывалась зависимость параметра α и / или неоднородности вращения от магнитного поля . Уменьшение α с увеличением напряженности поля приводит к уменьшению эффективного дина мо - числа , и рост поля останавливается . Есть , одна ко , основания полагать , что магнитная диффузия η также зависит от магнитного поля и также уменьша ется , когда поле усиливается . Большие времена жизни солнечных пятен по сравнению со временем линейной диффузии объясняют подавлением эффек тивной диффузии сильным магнитным полем [Pet-rovay, Moreno-Insertis, 1997]. Уменьшение диффузии с напряженностью поля предсказывает квазилинейная теория турбулентных коэффициентов переноса [Kitchatinov, et al., 2004b].

В данной работе используется модель αΩ - дина - мо для конвективной оболочки звезды . Магнитное поле симметрично относительно оси вращения :

ur r I r

B = e ф B + rot I e ф

A x sin θ

где x , θ и ϕ – обычные сферические координаты , e ϕ – единичный вектор в азимутальном направлении , B – тороидальная составляющая магнитного поля , A – потенциал полоидального поля .

Уравнения динамо в безразмерных переменных имеют вид дB  D ( df dA df dA

=- dt x V дx дв dO dx бенности нелинейного динамо вблизи критической величины динамо-числа. Относительная величина Deff/D как функция магнитного поля показана на рис . 1.

Величина f в (3) определяет неоднородное вра- щение, т. е. средняя скорость u дается выражением u = eφxsinθΩ f (x,θ).

Использовалась аппроксимация данных гелио сейсмологии о внутреннем вращении Солнца [Belvedere, et al., 2000]:

f ( x , О ) =--- У cos 2 m I--О I     C_x " .     (7)

nm

⁴⁶¹ m = 0     V V ²     J J n = 0

Значения коэффициентов C nm приведены в работе ( см . табл . 1, [Belvedere, et al., 2000]).

1 д fф ^{( B} ) д (sin O B ) ) 1 д f д ( xB ) ) + 3"I ^ф п ^{( B )—} I ’ x дО^ sin O    дО    J x ax V        д x J

∂ A

= φ ( B ) x cos θ sin³ θ B + ∂ t

Использовались псевдовакуумные граничные условия на поверхности ( x =1) и условия для поверхности раздела со сверхпроводником в основании ( x =0.7) конвективной оболочки :

д 2 A  Фп( B ) . A f 1   д A

+ Ф_П ( B )—— + ¹—sin О— I-—— x² x² д О V sin О д О

.

B = 0,

∂ A _{= 0,}

x = 1,

Уравнения справедливы в следующих прибли жениях . Рассматривается простейший случай , когда фоновые турбулентная диффузия η и альфа - эффект α однородны в пространстве . Зависимость от коор динат появляется лишь из - за нелинейности , т . е .

влияния магнитного поля :

η _T = ηφ_η ( B ), α _T = α cos θ sin² θφ_α ( B ).           (4)

^{∂ ( xB )} = 0, A = 0, x = 0.7. (8) ∂ x

На полюсах ( θ =0, π ) B и A обращаются в ноль . Симметрия полей относительно экватора задана не была , и дополнительные условия на экваторе не использовались . Эволюция поля во времени от некоторого начального заданного распределения рассчитывалась численно .

Здесь обезразмеренное поле B измеряется в единицах поля равнораспределения B_eq = 4 πρ u ′ , где u ' – среднеквадратичная скорость турбулентных движений . Зависимость от магнитного поля опреде ляем согласно расчетам коэффициентов переноса в квазилинейном приближении [Kitchatinov, et al., 1994b; Rüdiger, et al., 1993]:

φ α ( B )

32 B ⁴

_{1 -}    4 B ²

3(1 + B ²)²

1 - B ² B

arctg( B )

3 L

Ф п ( ^B ) = ^T I ¹ +

8 B V

4 + 8 B ²

(1 + B ²)²

+

B ² - 5 arctg( B ) .

B            J

Для сильных полей B >>1 магнитная диффузия уменьшается обратно пропорционально B , 3 π                          15 π

φ -     , в то время как φ -      . Поэтому если

^η 16 B                     ^α 64 B ³

вместо величины (1) рассмотреть эффективное ₃ α φ ( B )

динамо - число , D = Ω R ^{3     α} , с учетом зави -

( η φ η ( B ))

симости магнитной диффузии и α от магнитного поля , то для сильных полей такое число убывает с увеличением B , D _eff ~ B ^{- 1} , что и требуется для на сыщения роста поля . Однако для слабых полей при B <<1 находим ф_а "- 1 - 12 B ²/7 и ф_п ■- 1 - 2 B ². Поэтому D eff ■- D (1 + 16 B ² /7) первоначально возрас тает с B . С этим и связаны обсуждаемые ниже осо -

Флуктуации α

Параметры α и η связаны с турбулентной конвекцией . Поэтому в них присутствуют случай ные флуктуации . Оценка характерного масштаба времени таких флуктуаций по порядку величины есть l u ′ , где l – масштаб конвективных движений . В безразмерных единицах времени , принятых в урав -

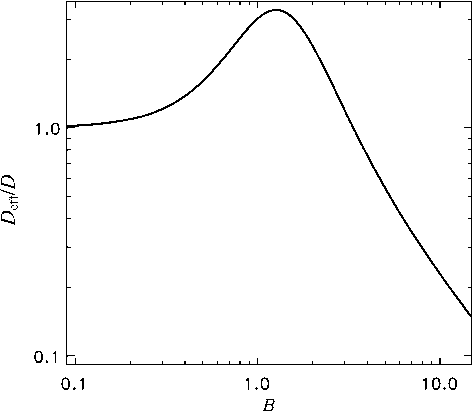
Рис . 1. Зависимость D _eff / D = φ_α ( B ) / φ ² _η ( B ) от магнит ного поля не является монотонной . Для слабых полей D _eff возрастает с B .

нениях (3), характерное время флуктуаций τ ~ lη u′R2 . Используя обычную оценку коэффициента диффузии η ~ lu′ , окончательно находим l2

τ =      .

R ²

Амплитуду флуктуаций оценить сложнее. Если предположить, что для отдельной конвективной ячейки характерная величина флуктуаций сравнима со средней величиной, то для относительной величины флуктуаций δα α ~ 1 N , где N – коли- чество конвективных ячеек. Вероятно, основной вклад в альфа-эффект для Солнца дают гигантские конвективные ячейки , размер которых сравним с толщиной конвективной оболочки, тогда N ~ l2/R2 ~ τ–1.

Ограничимся простейшей моделью, которая учитывает лишь флуктуации α, причем их относительная величина δα/α однородна в пространстве, но зависит от времени. Эта величина остается постоянной в течение времени τ (9), затем мгновенно изменяется и т. д. Уравнение для полоидального поля вместо записанного в (3) теперь примет вид

∂ A

= (1 + s τ)φ_α( B ) x cosθ sin³ θ B +

∂ t

∂ ² A φ ( B )      ∂     1   ∂ A

+Фп (B)—г + п о  sin 9—I-- dx2     x2       d9 v sin 9 d9

.

Здесь s – случайная величина с однородным распределением значений в интервале –1 ≤ s <1. Эта величина остается постоянной в течение времени τ , после чего мгновенно изменяется случайным обра зом . Расчеты проводились для l=0.2R( τ =0.04).

Результаты и обсуждение

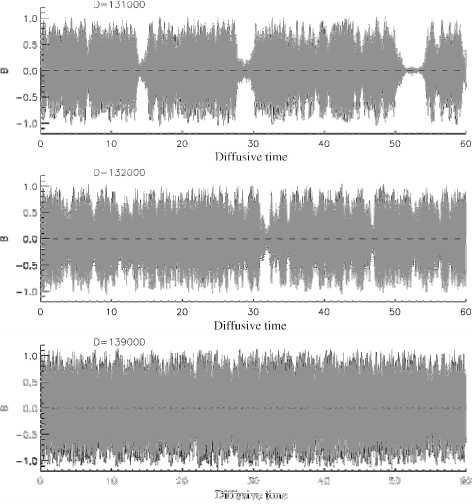
Рассмотрим сначала результаты для случая, когда флуктуации α отсутствуют, т. е. предельный случай малых времен корреляции τ → 0 . Изложенная выше модель показывает следующее поведение. Критическое динамо-число линейной задачи Dcr=131000. При меньших значениях D магнитное поле затухает со временем, а при D>Dcr – возрастает. Период динамо-цикла в безразмерных единицах времени составляет около 0.02. Нелинейные расчеты обнаруживают более сложное поведение. Во всех проведенных расчетах распределение поля становится антисимметричным (дипольный тип симметрии) относительно экваториальной плоскости по прошествии достаточно длительного времени (рис. 2). На рис. 3 показана зависимость амплитуды колебаний тороидального поля от динамо-числа (поле приводится в безразмерных единицах; для Солнца B=1 соответствует примерно 5000 Гс). Даже при небольшом превышении величиной D критического значения устанавливаются колебания со значительной амплитудой B~1. Для D, меньших критической величины, но близких к ней, результат зависит от величины начального поля. Слабые поля неограниченно затухают, в то время как для достаточно сильных начальных полей устанавливаются колебания конечной амплитуды. Конечные ампли- туды колебаний при D

Гистерезисный характер зависимости, показанной на рис. 3, является следствием подавления турбулентной диффузии магнитным полем. Зависимость эффективного динамо-числа от магнитного поля, показанная на рис. 1, не является монотонной. Если начальное магнитное поле мало, то Deff меняется мало, и при D<Dcr поле затухает. Однако при достаточно большом начальном поле Deff может превысить критическое значение, даже если D<Dcr, что приводит к усилению поля. Насыщение роста поля происходит в области сильных полей, где кривая рис. 1 имеет отрицательный наклон.

В области гистерезиса на рис. 3 имеется два возможных режима: затухающие колебания малой амплитуды и установившиеся циклы относительно большой амплитуды. Наблюдения магнитной активности Солнца также обнаруживают перемежаемость эпох относительно высокой активности с глобальными минимумами. Можно ожидать, что флуктуации спираль-

Рис. 2. Конфигурация диполя в меридиональном сечении конвективной зоны. В левой части показаны изолинии тороидального магнитного поля, а в правой части – изолинии полоидального поля.

D

Рис. 3. Амплитуда колебаний тороидального магнитного поля в середине конвективной зоны (x=0.85, θ=π/4) как функция динамо-числа (1).

ности (α–эффекта) в рассматриваемой модели позволят воспроизвести перемежаемость. Флуктуации могут приводить к переходам между двумя возможными режимами в области гистерезиса.

Рисунок 4 показывает, что такие переходы действительно имеют место, если динамо-число лишь немного превышает критическую величину. По мере увеличения D уменьшаются частота появления и продолжительность моделируемых глобальных минимумов. При достаточно больших D они вовсе исчезают. С уменьшением D глобальные минимумы в расчетах становятся более продолжительными, и при достаточно малых D динамо «выключается» (установить точное значение D, при котором это происходит, в численных расчетах с флуктуирующим α затруднительно).

Рассмотренная модель показывает глобальные минимумы лишь вблизи критической величины динамо-числа. Заметим, что число D (1) является возрастающей функцией скорости вращения . Скорость вращения Солнца и подобных ему звезд уменьшается со временем [Skumanich, Astrophys, 1972]. Причем между динамо и вращением имеется обратная связь: чем выше магнитная активность, тем больше скорость потери углового момента [Durney, Latour, 1978]. Возможно, что замедление вращения в конце концов приводит звезды к порогу действия крупномасштабного динамо. Состояния низкой активности действительно наблюдаются лишь на старых звездах [Wright, 2004].

Если предложенная картина верна, то наблюдения могут обнаружить резкое уменьшение темпов замедления вращения для старых звезд, показываю-

Рис. 4. Зависимости магнитного поля от времени для ряда значений динамо-числа (1), близких к его критической величине D_cr=131000, полученные в модельных расчетах с учетом флуктуаций параметра α. Значение поля берется в середине конвективной зоны (x=0.85, θ=π/4). В верхней части каждого рисунка проставлено соответствующее динамо-число.

щих глобальные минимумы активности. К этому вопросу можно подойти иначе. Характерное время замедления вращения Солнца из-за истечения солнечного ветра есть

T = ^3I dec   _2Rc2_M&^,

где I – момент инерции Солнца, Rс – радиус коротации в солнечной короне, M – скорость потери массы Солнца. Подставляя численные значения I=5.7⋅10⁵³ [г⋅ см²], Rc ~ 10R₀ и Ml ~ 2.510^-14M_@[год^-1] в (11), находим оценку T_dec = 3.5 ⋅10¹⁰лет, что существенно превышает возраст Солнца. Иными словами, замедление вращения Солнца уже практически остановилось. Это согласуется с предположением о том, что скорость вращения Солнца близка к пороговой для включения динамо.

Работа выполнена при поддержке РФФИ (проекты 10-02-00148-а, 10-02-00391) и СО РАН (Лаврентьевский грант 2010-2011).