Модель пригодности системы технического обслуживания по состоянию радиоэлектронной аппаратуры и способ ее построения

В последнее время в ходе научно-исследовательских и опытно-конструкторских работ приобретен существенный опыт в разработке методологии построения систем технического обслуживания (СТО) радиоэлектронной аппаратуры (РЭА) [1; 4–6; 9]. Однако их анализ [1; 3; 5; 6; 9] показывает, что разработанные теоретические положения не позволяют в полной мере строить эффективные системы и требуют дальнейшего развития, которое невозможно без построения соответствующих моделей. В частности, для системы технического обслуживания по состоянию (СТОС) РЭА решены задачи по обоснованию параметров технического состояния (ПТС) РЭА, периодов технического обслуживания, уровня подготовки и количеству обслуживающего персонала (ОП), группировки ПТС, по методам прогнозирования значений параметров, определяющих техническое состояние РЭА, по методам группировки параметров РЭА, интервалам упреждения времени наработки изделия на отказ и так далее. Эти решения найдены при условии, что параметр потока отказов РЭА ω является стационарным, поскольку принято считать верной следующую его зависимость от времени эксплуатации (рис. 1).

Однако опыт эксплуатации РЭА показывает, что стационарный участок данной зависимости в действительности является нестационарным. Это объясняется, например, сменой сезонов (зима, весна, лето, осень), сменой местности эксплуатации РЭА, различными подходами к организации технического обслуживания и разным уровнем подготовки обслуживающего персонала. Кроме того, неодновременность работы элементов РЭА и наличие последействия отказов являются основанием утверждать, что параметр потока отказов сложной РЭА в принципе не может быть величиной постоянной, если даже параметры потока отказов элементов постоянны [7; 10].

Анализ имеющихся статистических данных по отказам сложной РЭА позволяет выявить следующие изменения параметра потока отказов во время эксплуатации: стационарные значения ω на различных уровнях и тренды возрастания и убывания ω . При этом наиболее опасным является возрастание ω с началом периода старения. Качественно данная зависимость представлена на рис. 2, из которого видно, что в процессе эксплуатации есть убывающие тренды ( 1 , 5 , 8 ), возрастающие ( 3 , 7 , 9 , 11 ) и стационарные значения различного уровня параметра потока отказов ( 2 , 6 , 10 ). Понимая, что система технического обслуживания по состоянию радиоэлектронной аппаратуры создается для предпо-

Рис. 1. Зависимость параметра потока отказов от времени эксплуатации (стационарный параметр потока отказов в период нормальной эксплуатации)

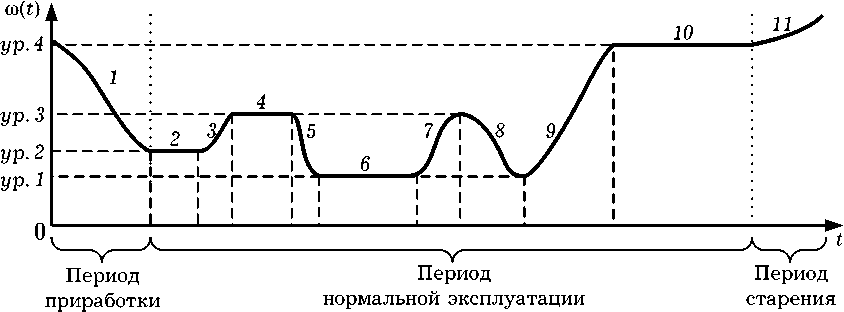
Рис. 2. Пример зависимости параметра потока отказов от времени эксплуатации (нестационарный параметр потока отказов на этапе нормальной эксплуатации)

лагаемого стационарного уровня (значения) параметра потока отказов ω, возникает вопрос: как себя «поведет» СТОС при возрастающих (убывающих) трендах, а также при смене уровня (значения) стационарного потока отказов ω, например, со 2-го на 4-й, потом на 6-й и на 10-й. То есть вопрос пригодности СТОС в таких ситуациях становится весьма актуальным. Это приводит к необходимости введения понятия пригодности системы технического обслуживания РЭА. В общем случае, под пригодностью СТО РЭА будем понимать свойство данной системы удовлетворять требованиям по показателям качества (эффективности) в соответствии со своим предназначением в существующих условиях эксплуатации. Учитывая, что назначением проведения СТО является поддержание работоспособности или исправности изделия [2], то в качестве предъявляемых требований целесообразно выбрать значения коэффициента готовности РЭА KГ и коэффициента технического использования РЭА KТИ. Существующие условия эксплуатации как раз и проявляются при использовании по назначению, ожидании, хранении и транспортировании и с учетом смены сезонов, местности эксплуатации РЭА, различных подходов к организации технического обслуживания, уровня подготовки обслуживающего персонала и так далее, определяют значение (изменение во времени) параметра потока отказов радиоэлектронной аппаратуры.

На основании этого получаем, что зависимость K _Г, K _ТИ = ϕ ( ω ) определяет модель пригодности СТО РЭА.

Учитывая, что система технического обслуживания определяется стратегией, своими параметрами и строится для конкретной РЭА, то модель пригодности не может быть некоторой универсальной зависимостью ϕ , поскольку изменение стратегии СТО, параметров СТО, смена радиоэлектронной аппаратуры приводят к изменению зависимости Π = ϕ ( ω ), где Π K _Г, K _ТИ .

Кроме того, задача построения модели пригодности СТО усложняется отсутствием требуемых статистических данных или даже невозможностью их получения в принципе и тем более для различной РЭА в различных условиях эксплуатации с различными стратегиями и параметрами СТО. Исходя из этого получаем, что для ее построения на первом этапе необхо-

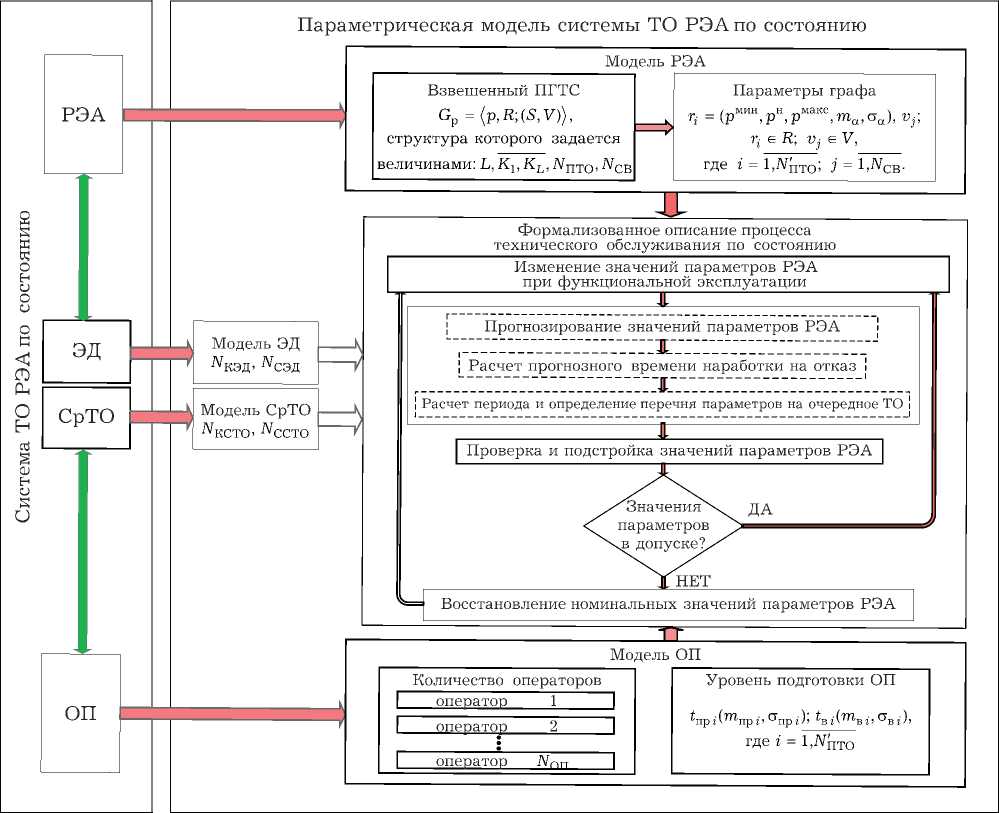
Рис. 3. Параметрическая модель системы технического обслуживания по состоянию радиоэлектронной аппаратуры

димо смоделировать СТО определенной стратегии с конкретными параметрами для конкретной аппаратуры, с выходными показателями K _Г и K _ТИ, в которой можно изменять «поведение» параметров технического состояния, тем самым устанавливать требуемое значение параметра потока отказов to , и, в конечном итоге, построить параметрическую модель. На втором этапе следует провести исследование на данной модели, в результате которого при изменении to определяется K _Г и K _ТИ, что позволяет получить модель пригодности П = ф ( to ).

Решим эту задачу для системы технического обслуживания по состоянию vстр2, которая характеризуется следующими параметрами (первый этап): периодом проверки T'; уровнем подготовки обслуживающего персонала UОП; средним временем проверки tпр; среднеквадратическим отклонением времени проверки стпр; средним временем восстановления tв; среднеквадратическим отклонением времени восстановления ств; системой параметров технического состояния РЭА Gp; минимальным значением параме-мин тра p ; максимальным значением параметра pмакс; номинальным значением параметра pн; параметром функции а; среднеквадратическим отклонением параметра функции са; коэффициентом связности между параметрами v; количеством обслуживающего персонала NОП; методами прогнозирования значений параметров, определяющих техническое состояние РЭА X; методами группировки параметров РЭА Mгр; интервалом упреждения времени наработки изделия на отказ А.

Учитывая вышесказанное, параметрическую модель СТО по состоянию представим как зависимость [5]

^{П (} v стр2 ) = ^f 2⁽ T , U ОП ^[ t пр , ^ пр , t в , ^ в ] ,

G p ^[ Р ^мин , Р ^макс , Р н , а , ^, v ] , N ОП , X , А , M гр ).

Состав такой модели представлен на рис. 3.

Система технического обслуживания представляет собой взаимодействие РЭА и персонала, которое осуществляется с помощью средств технического обеспечения на основе эксплуатационной документации. Радиоэлектронная аппаратура описывается взвешенным параметрическим графом технического обслуживания, структуру которого определяют следующие величины: количество уровней, количество параметров на каждом уровне, общее количество параметров и количество связей между параметрами. Каждая вершина графа взвешена кортежем r , каждое ребро – коэффициентом связанности двух параметров v. Обслуживающий персонал характеризуется количеством и уровнем подготовки к решению задач технического обслуживания и восстановления.

Описание взаимодействия компонентов параметрической модели во времени [3] определяется функционалом F' и представлено выражением:

F ' ( t ) =                                                        (1)

ОПИСАНИЕ ПРОЦЕССОВ ИЗМЕНЕНИЯ И ПРОГНОЗИРОВАНИЯ ЗНАЧЕНИЙ

ПАРАМЕТРОВ РЭА ПРИ ФУНКЦИОНАЛьНОЙ ЭКСПЛУАТАЦИИ изменение значений параметров

Pi (tn) = рнеan(tn-T^ + ^N™ Vij (еain(tn-T^ - 1), при 0 < tn < T‘; i = 1,Nпто, i * j, n = 1,2,..., an = ГНзр(mai, oai);

P i. „( t n ) = P i ^{+ 1(} 6 1 P i ⁽ t n - 1 ) ^{+ 0} 2 P i ⁽ t n - 2 ) ⁺ ...

AR            p

... + 0 ? P i ( t n - i )) + 0_V P j ( t ) + s t ,

P i „ Д t n ) = ( Ф z P i ⁽ t n ) ⁺ Ф Z + 1 P i ⁽ t n - 1 )) ^{+ s} t ,

ES i = 1,NПТО, ? = 1,2,..., V = 1,2,..., Z = 1,2,...; расчет времени наработки на отказ t 0 i = tA

t          макс(мин)

^P i ⁽ t n ) ^P i

P i ⁽ t n + 1 ) ^- P i ⁽ t n )

, i = 1, ^N ПТО ,

макс              мин

P i ⁽ t o ) >  P i      или P i ⁽ t o ) <  P i   ;

расчет периода технического обслуживания

T* = arg max K _r ( T '), при K ти >  K ти зад ;

ОПИСАНИЕ ПРОЦЕССА ПРОВЕРКИ

И ПОДСТРОЙКИ ЗНАЧЕНИЙ ПАРАМЕТРОВ

РЭА ПРИ ТЕХНИЧЕСКОМ ОБСЛУЖИВАНИИ

Pi (tn) = Pi (t o + TT), при (t o + T') < tn < (t o + T ‘ + tожi) и

P i ( t n ) = P i ( t o + T ' ) - ^[ P i ( t o + T ' ) - P i ^{1 ]} x

A

е ⁽ t n ^- t o ^- T ^- t ож i ^- t пр i ) е ^{( -} T ^- t ож i ^- t ^п р i )

при ( t _n + T ‘ + t ) <  t„ <  0         ож n

< (to + T + tожi + tпрi), m-1

tожi =2 tпр(k+rNОП) +£ tвr, r=o tпрi = Гнзр(mпрi, ^прi), для параллельных проверок

(независимых параметров):

---------;--------- ,I i = 1,NT   , k = остаток ----

ПТО

IN ОП i - k m=     ;

N _ОП

для последовательных проверок (зависимых параметров):

i = 1, N Пто , k = N on = 1;

ОПИСАНИЕ ПРОЦЕССА ВОССТАНОВЛЕНИЯ НОМИНАЛьНыХ ЗНАЧЕНИЙ

ПАРАМЕТРОВ РЭА

P i ⁽ t n ) = P i ⁽ t o ⁺ T ) ^- [ P i ⁽ t o ⁺ T ) ^- P i ¹ ] ^x

x

A е (tn - t o - T - tожi - tпрi - tвi )   е (-T - tожi - tпрi - tвi )

при ⁽ t o + T + t ож i ⁺ t пр i ) <  t n <

< (tn + Tf + ^жi + t + t ),

0 ожi прi вi i = 1,N ПТО, t в i = Гнзр( m в i, У в i).

Функционал представляет собой систему выражений: первое и второе описывают изменение и прогнозирование значений параметров в процессе функциональной эксплуатации, третье описывает проверку и подстройку значений параметров РЭА при техническом обслуживании, четвертое описывает восстановление номинального значения параметра в случае его отклонения за пределы допуска.

Для получения модели пригодности СТОС П ( v _ст р2 ) = Ф 2 ( ю ) на основе параметрической модели разработана инструментальная среда выбора рациональных параметров системы технического обслуживания по состоянию [8]. Ее интерфейс представлен на рис. 4.

Используя ее возможности, параметрическую модель СТОС настраиваем на конкретную РЭА, определяя параметры G _p, и собственные параметры СТО: T' , U on , N on , х , M гр , A .

После настройки параметрической модели СТОС РЭА можно приступать к построению модели пригодности СТОС РЭА (второй этап).

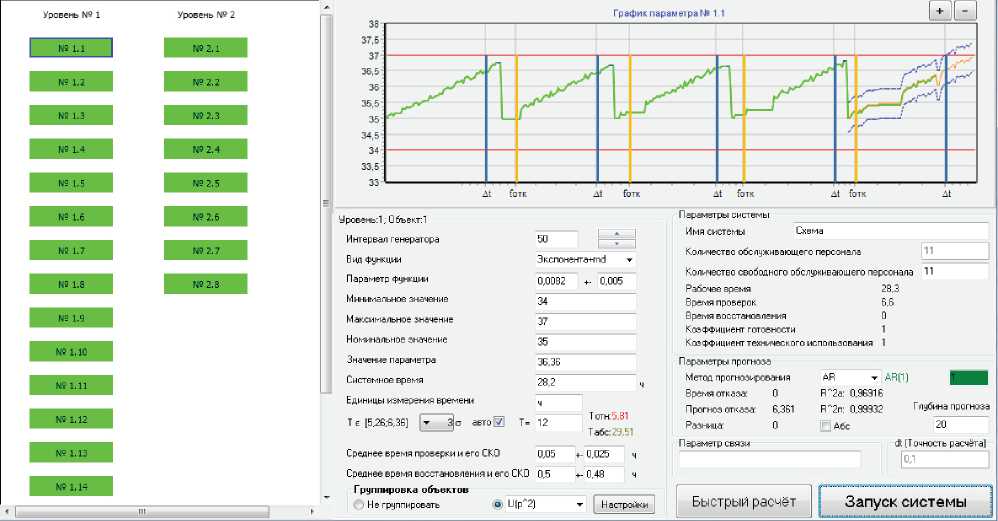
Рис. 4. Интерфейс инструментальной среды выбора рациональных параметров системы технического обслуживания по состоянию

Для этого необходимо выполнить следующие процедуры:

• 1.    Сформировать статистический ряд П ( v _СТ р2 ) = = Ф2И ;

• 2.    Определить функцию ф 2 полученного статистического ряда.

Формирование статистического ряда заключается в следующем (рис. 5).

Для выполнения первой процедуры в параметрическую модель СТОС РЭА вносятся параметры РЭА в виде значений параметрического графа технического состояния G _p, который формирует поток отказов to . Для проведения полноценного эксперимента и получения требуемой информации осуществляются многократные прогоны модели на ЭВМ при различных значениях to . В результате этого получаются численные значения параметров K _Г, K _ТИ для РСТО с различными значениями параметра потока отказов to .

Сглаживая гистограмму, построенную по статистическому ряду, получили модель пригодности конкретной СТОС РЭА. Качественно она имеет следующий вид (рис. 6).

Задавая условия Kг > Kг Зад, Kти > Kти зад на модели пригодности, можно принимать решение о пригодности СТОС. Как правило, в качестве основного показателя принятия решения выбирают KГ, а KТИ находится в ограничении. Такой подход обеспечивает нахождение максимального KГ при заданном временном соотноше- нии «время функционирования – время обслуживания» путем настройки параметров СТОС.

Проанализируем модель пригодности СТОС РЭА (рис. 6).

Зная значения K _{Г зад}, можно определить допустимые значения параметра потока отказов to _доп. Тогда получаем, что в пределах |^ 0; to _доп ] СТОС РЭА пригодна к использованию независимо от «поведения» to ( t ). То есть в данных пределах не имеют влияния различные уровни и тренды параметра потока отказов (рис. 2). Если значения to ( t ) превышают to _доп, то СТОС РЭА применять нецелесообразно. В такой ситуации необходимо принимать решение о коррекции параметров СТОС.

Кроме того, в результате исследования с использованием инструментальной среды (рис. 4) получили следующее. Увеличение параметра потока отказов to ( t ) приводит к уменьшению коэффициента готовности РЭА. Такое уменьшение носит плавный характер и крутизна зависимости K г ( v _ст р2 ) = Q 2 ( to ) небольшая. Такое «поведение» СТОС можно объяснить физической сущностью стратегии, в которой параметры системы технического обслуживания за счет прогноза параметров технического состояния РЭА подстраиваются под параметр потока отказов to ( t ). Однако СТОС является инерционной системой с запаздыванием прогноза на один период принятия решения о проведении ТО, что приводит к пропуску отказов при увеличении to ( t ) и, как

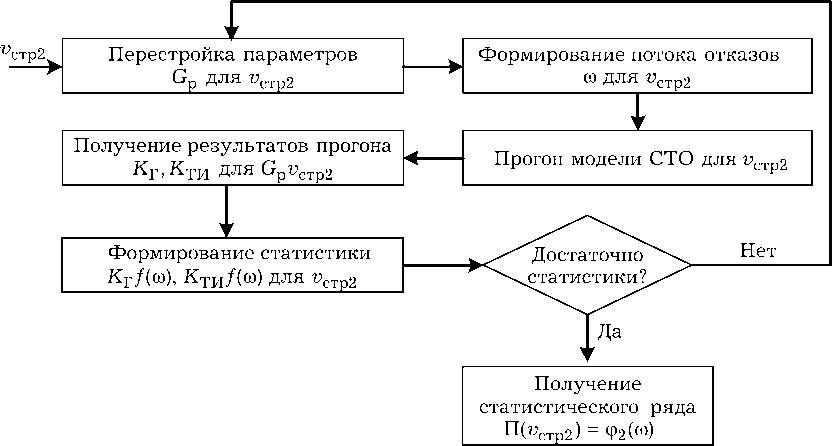
Рис. 5. Формирование статистического ряда Π ( v _стр2) = ϕ ₂( ω )

следствие, к незначительному снижению K _Г. Подстройка СТОС под параметр потока отказов заключается в изменении периода проверки T ′ , методов прогнозирования значений параметров, определяющих техническое состояние РЭА χ ; методов группировки параметров РЭА M _гр; интервала упреждения времени наработки изделия на отказ ∆ ; что при увеличении ω ( t ) приводит к резкому увеличению среднего времени технического обслуживания РЭА T _ТО и, следовательно, к резкому снижению коэффициента технического использования K _ТИ. В результате зависимость K _ТИ( v _стр2) =ϕ ₂( ω ) имеет существенно большую крутизну по сравнению с зависимостью K _Г( v _стр2) =ϕ ₂( ω ). При изменении значений t _пр, σ _пр, t _в, σ _в, N _ОП, χ , M _гр, ∆ можно поддерживать значения K _Г и K _ТИ на заданном уровне и менять крутизну спада данных параметров.

Учитывая вышесказанное, можно выделить два основных этапа получения модели пригодности СТОС (рис. 7): построение параметрической модели и формирование зависимости K _Г, K _ТИ =ϕ ₂( ω ). Основу первого этапа составляет описание процессов изменения значений параметров, прогнозирования значений параметров, проверки и подстройки значений параметров, процессов восстановления значений параметров РЭА. Основу второго этапа составляет настройка параметрической модели на конкретную РЭА и индивидуальные параметры СТОС, формирование требуемых статистик на основе параметрической модели СТОС и определение функции полученного статистического ряда. Имея модель пригодности СТОС РЭА, можно принимать ре-

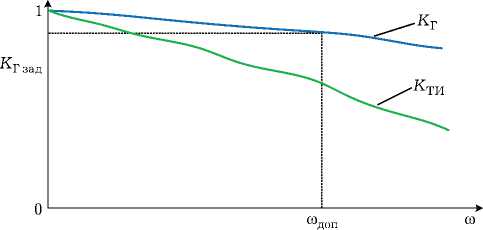
Рис. 6. Модель пригодности СТОС РЭА шения о целесообразности использования или перестройки параметров применяемой СТО, то есть принимать решение о ее пригодности при заданном «поведении» параметра потока отказов ω.