Модель радиальных утечек с циркуляцией в однозаходных шнековых машинах

Предложена новая модель утечек через радиальный зазор между гребнем шнека и внутренней поверхностью корпуса в однозаходных шнековых машинах. Основным недостатком существующих моделей является то, что поток утечек выносится за границы канала и больше не участвует в процессе течения, хотя на практике происходит перетекание материала из одного витка шнека в другой, сопрягающийся с ним через реборду. Общая идея подхода и, в то же время, отличительная особенность заключается в том, что при моделировании течения в канале баланс массовых расходов через основной канал и зазор выражается через дополнительное дифференциальное соотношение, а интенсивность расхода утечек с учетом распределения давления по длине канала определяется функциональной зависимостью с запаздывающим аргументом. На примере изотермического течения линейной вязкой жидкости в прямоточном шнеке рассмотрено влияние радиального зазора, угла нарезки и ширины реборды на интегральные характеристики процесса. Построены поверхности границы устойчивости течения в канале шнека.

MODEL OF RADIAL LEAKAGES WITH CIRCULATIONIN SINGLE-THREADED SCREW EXTRUDERS

E.V. Slavnov, A.I. Sudakov and C.V. Buzmakova

Institute of Continuous Media Mechanics UB RAS, Perm, 614013, Russia

A new model of leakages through the radial clearance in single-threaded screw extruders is proposed. The weakness of the existing models is that the leakage flow is carried outside the boundaries of the channel and does not participate in the flow any longer, although in real conditions the material migrates from one flight of the extruder channel to the other conjugated via the flight land. The general idea of the approach and its main distinguishing feature are as follows. In simulation of the channel flow, the balance of mass discharges through the main channel and clearance is expressed as an additional differential relationship, and the intensity of the leakage flow, with consideration of pressure distribution throughout the channel length, is defined by the functional dependence with the delayed argument. An example problem on the isothermal flow of linear viscous flow fluid in the straight – flow extruder has been solved to examine the influence of radial clearance, angle of rifling and the width of flight on the integral characteristics of the process. The surfaces of flow stability boundary in the screw channel are constructed.

В реальных условиях в одношнековых экструдерах всегда существует радиальный зазор между гребнем шнека и внутренней поверхностью корпуса. Величина зазора меняется в диапазоне от 0,1 мм до 1 мм и более в зависимости от предназначения оборудования и диаметра шнека. В процессе эксплуатации этот зазор может увеличиваться по мере износа сопрягаемых деталей. Особенно быстро это происходит при работе с композициями, содержащими абразивные частицы, например, мелко дисперсные ферритовые порошки. В некоторых случаях зазор увеличивается специально, в частности, для создания условий качественного смешения отдельных компонентов или для дополнительного сцепления материала со стенкой корпуса.

Наличие радиальных зазоров существенно влияет на рабочие характеристики шнековых машин. Мор и Маллок [1] впервые предложили метод учета утечек материала через радиальный зазор при течении ньютоновской жидкости в изотермическом режиме течения. Дальнейшее развитие и модификацию модель нашла в работах [2–5]. Основным недостатком модели и ее модификаций является то, что поток утечек выносится за границы канала и больше не участвует в процессе течения, хотя на практике происходит перетекание потока утечек из одного витка шнека в другой, сопрягающийся с ним через реборду. Подобный подход рассмотрен в статье [6], но там учитываются утечки лишь с одной стороны канала.

В настоящей работе предлагается новая модель утечек через радиальный зазор на примере течения вязкой жидкости в одношнековом однозаходном экструдере. Интенсивность потока утечек зависит от градиента давления. В тоже время, градиент давления определяется потоком утечек. Отсюда возникает связанная задача — поток утечек рассматривается в качестве распределенной обратной связи по основному потоку. В каждой точке канала шнека происходит приток и отток материала через зазоры из точек, расположенных в соседних витках шнека, удаленных от рассматриваемой точки на расстояние равное длине витка шнека (Рис. 1). Общая идея подхода заключается в том, что при моделировании течения в канале баланс массовых расходов через основной канал и зазор выражается посредством дополнительного дифференциального соотношения, а интенсивность расхода утечек с учетом распределения давления по длине канала определяется функциональной зависимостью с запаздывающим аргументом. Предложенная постановка снимает ряд трудностей (организация итераций по потоку утечек, устойчивость численной процедуры, задание распределения потока утечек по сечению основного потока и т.д.), которые возникают при численной реализации модели двумерного течения в канале шнека с учетом изменяющегося по длине канала потока утечек

Для описания течения расплава полимера в канале экструдера рассматривается обращенное движение (шнек считается неподвижным, а корпус экструдера — движущимся со скоростью и р = п п об D k /60) и выбирается развернутое на плоскость его среднее сечение. В этом случае скорость определяется соотношением

+ и - -y- , h ( х )

V ( x , y ) = ^.dP . 4- -

2 -ц dx [ h ²( х ) h ( х )

где и = up sin ф — скорость подвижной стенки вдоль развернутого на плоскость канала; nоб — скорость вращения шнека (об/мин); Dk — внутренний диаметр корпуса шнека; dP ф — угол нарезки канала; — — градиент давления вдоль канала; h(x) — глубина dx нарезки канала, в общем случае, слабо меняющаяся по длине канала; ц — динамическая вязкость жидкости (расплава); y — координата по высоте канала; x — координата вдоль оси канала. После интегрирования уравнения (1) по высоте канала и умножения расхода в среднем сечении на ширину канала получается следующее выражение для секундного объемного расхода:

Q ( x ) = -

h ³( x ) - b dP +

12 ц    dx

и ■ h ( х ) - b

где b — ширина канала.

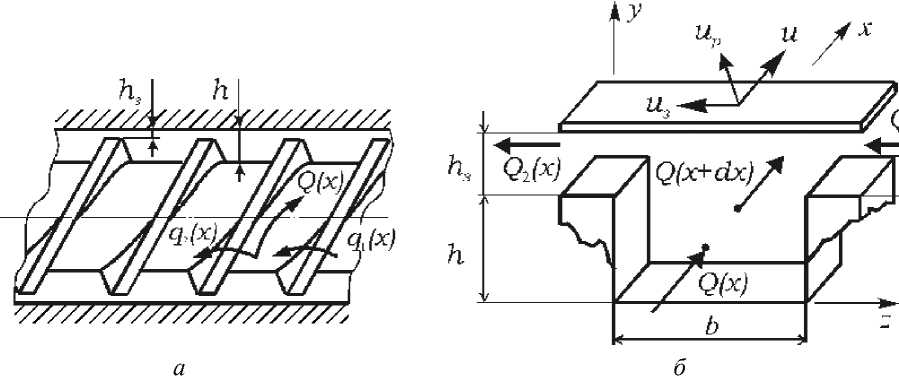
Рис. 1. Схема перетекания материала в канале шнековой машины ( а ) и плоская модель каналов ( б )

Между корпусом и ребордой шнека имеется радиальный зазор (Рис. 1). Для записи уравнения баланса объемных расходов с учетом возможных утечек через радиальные зазоры в канале шнека, развернутом на плоскость, выделяется элементарный объем в сечении канала длиной dx Уравнение баланса объемных расходов записывается как

Q ( x + dx ) - Q ( x ) = Q i ( x ) - Q 2 ( x );

где

Q ( x ) = j J V_x 1 dydz и Q ( x + dx ) = J J V_{x 2} dydz

соответственно втекающий и

zy вытекающий потоки через

zy сечения канала   шнека;

Qi( x) = JJ Vz 1 dydx   и xy

Q2( x) = JJ Vz 2 dydx — втекающий xy и вытекающий потоки через сечения радиального

зазора.

Левая часть уравнения (3) определяет изменение расхода по каналу шнека dQ(x) = Q(x + dx) - Q(x) на участке dx, а правая может быть записана следующим образом: Q1 (x) - Q2 (x) = J [ q1 (x) - q 2 (x)] dx,

x

где q i⁽ x ) = J V z 1 dy и q 2 ⁽ x ) = J V z 2 dy ^— yy

интенсивность притока и оттока утечек через радиальные зазоры соответственно. С учетом сказанного уравнение баланса расходов (3) приводится к виду dQ (x) = J[ q1( x) - q 2( x)] dx или   Q(x) = q1( x) - q 2( x).

x

В каждой точке по координате x могут иметь место утечки: с притоком интенсивностью q 1 (x) и оттоком интенсивностью q 2 (x) , которые определяются перепадом давления в сопрягаемых точках, расположенных по разные стороны реборды.

При условии, что рассматривается течение в плоскости, перпендикулярной образующей реборды, и используя прежнее приближение, после интегрирования уравнения для скорости перетекания по высоте зазора между ребордой шнека и корпусом h з , выражения для интенсивности утечек приводятся к виду:

qP x ) =

h з ³( x )

12 -ц- b₃

[P(x) - P(x - Ax)] + u3h2(х)

, . h 3 ( x -A x )_Гп,                        uh ( x )

q 2 ^{( x} ) = —r^- [ P ^{( x A x} ) ^- P ^{( x - 2 A x} ) ] ⁺—, 12 -ц- b                            2

где h з (x) — величина зазора между гребнем реборды и внутренней поверхностью корпуса (в каждой точке сечения канала величина постоянная, но в общем случае может меняться по длине развернутого канала); b з — толщина реборды (длина канала перетекания); A x — длина витка шнека по образующей; и з = и р cos ф — скорость подвижной стенки в канале перетекания.

При заданном расходе Q ₀ , например, со стороны прессующего инструмента или дозирующего (шестеренчатого) насоса, выражение (4) записывается как

x

Q ⁽ x ) = J [ q i ⁽ x ) ^- q 2 ⁽ x ) ] dx + Q 0 .

Это уравнение используется после определения Q(x) , q 1 (x) , q 2 (x) для контроля выполнения баланса расходов в каждой точке по оси развернутого канала шнека.

В результате получается система уравнений (2), (4) и (5) с граничными условиями:

Q (0) = Q ₀; P (0) = P

Для приведения переменных к безразмерному виду вводятся следующие комплексы:

Q=, .Q; p=a------^p;    q=—тq;

и -h -b              6-ц - и -1               и -h

- x a- A x       -      h ( x )      ~ . . h ( x )

.x = —;     A x = —;     h (. x ) =----;     h , ( x ) = —---.

ll    hзh

И исходная система уравнений, и граничные условия преобразуется к виду:

dP ( x ) = 4- -      Q! ( x );

dx     h ³( l x ) h ²( x)

^{dQ (}- x )    А

= A i n [ q i ^{( x} ) ^- q 2 ^{( x} ) ] ;

dx qi (.x) = А1 n kb3 hi3 (x) [P3(jx) - P3(x - Ax)] + В hi3 (.x);

q₂ (J x ) = А ₁ n k_b3 h¹₃ ³ (. x - A x ) [ P (X - A x ) - P (J x - 2 A x ) ] + В h¹₃ ( x - A x );

Q (0) = Q o ; P (0) = P o ,

В выражениях (8) также используются обозначения: А ₁ = (Ур+Р):)- ; в = tg ф ; к_ь з = А;

sin2 9                     b₃

, cos ф кн = ——; n kbз

количество витков шнека. Из уравнений (8) следует, что в рассмотренном случае решение зависит от характера изменения как h(5c) , так и hз (х), а не только от их отношения, как было показано в работе [6].

В частном случае, когда величина зазора между гребнем реборды и внутренней поверхностью корпуса h _з и глубина нарезки h на шнеке постоянны, система уравнений (8) принимает вид:

dP ( xc) _ 1 dx

пи

Q ( x );

dQ(x)    Л Г ~ Z ~

^_ A n [ q i ⁽ x ) ^- q 2 ⁽ x ) ] ;

dx q (x) _ А1 n kb3 kV [P(x) - P(x -Ax)] + В kv;

q₂ ( x ) _ А n k_b3 k V [ P ( x - A x ) - P ( x - 2 N x ) J + В k_v x (x - A x );

x

Q ( x) _ Q ( x) - A J[ q , ( x) - q ₂ ( x ) ] dx ,

h где k _ -;; /(x - Ax) — единичная функция Хевисайда.

v h

Для решения системы уравнений (9), (10) используется программное средство «Matlab». На рисунке 2 представлен вариант решения, полученный при следующих исходных данных: Q0 _ 0,5; P0 _ 0 ; ф_ 17°; n _ 20; kb3 _ 10; kv _ 0,15. Этот вариант демонстрирует наиболее интересные особенности предлагаемой модели. На рисунке приведены изменения по длине развернутого канала интегральных характеристик потока: давления P*(x); объемного секундного расхода по каналу шнека Q(x);

интенсивности утечек через зазоры 1(. x ), 2(. x ) и qj ( xc) _ q , ( x ) - q ₂( x ); объемного секундного расхода по экструдеру в целом Q ₀ , вычисленного по выражению (10). Из рисунка видно, что градиент давления имеет нелинейный характер, несмотря на ньютоновские свойства жидкости. Условие постоянства расхода с учетом утечек сохраняется на всей длине канала (прямая 6 на Рис. 2). В то же время, течение по каналу шнека происходит с секундным расходом, превосходящим Q ₀ . Секундный объемный расход Q (. x ) увеличивается вдоль канала от 0,5 до 0,8 и устанавливается на уровне 0,75

за счет доли потока утечек в расходе по каналу шнека. На начальном участке интенсивность утечек притока из одного соседнего витка и оттока жидкости в другой виток не равны между собой, что приводит к колебаниям интенсивности утечек cj (. x ), объемного расхода Q (. x ) и давления 7 ^е (. x ). Вопрос об устойчивости решения всегда вызывает интерес, но в данном случае определение границы устойчивости — это, прежде всего, возможность определить степень влияния основных конструктивных факторов, таких как k v , k b _з, n и ф на характер течения при наличии радиальных зазоров.

Изменение характера течения при возрастании k_v (остальные параметры модели остаются прежними) показано на рисунке 3. Значение k_v = 0,08 (Рис. 3, а ) определяет величину зазора между ребордой и корпусом шнека, сопоставимую с допусками на их изготовление. Следует обратить внимание, что практически нулевые перетекания q (. x ) увеличивают расход по каналу шнека Q ( 5с ) на 12%. С увеличением относительного

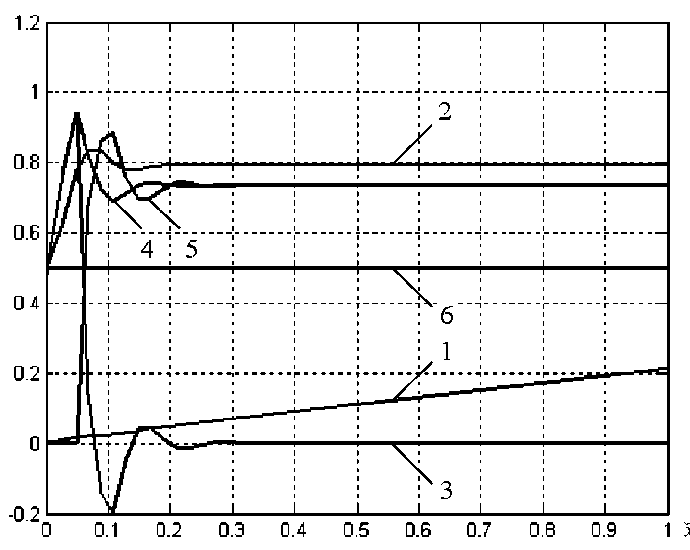
Рис. 2. Изменение интегральных характеристик потока по длине канала экструдера:

1 — Р ( х); 2 - Q ( x); 3 - <7( x) - 10; 4 - , ( x) - 10; 5 - ^С x) - 10; 6 - Q_o(x)

размера зазора k_v колебательный характер движения распространяется вдоль канала (Рис. 2) и в результате течение становится неустойчивым. Границе устойчивости соответствуют условия, когда амплитуда колебаний расхода Q ( Х ) или давления P ( x ) остается постоянной вдоль канала. Затухание амплитуды указывает на устойчивость решения, а возрастание — на неустойчивость решения. На рисунке 3, б представлены характеристики течения на границе устойчивости.

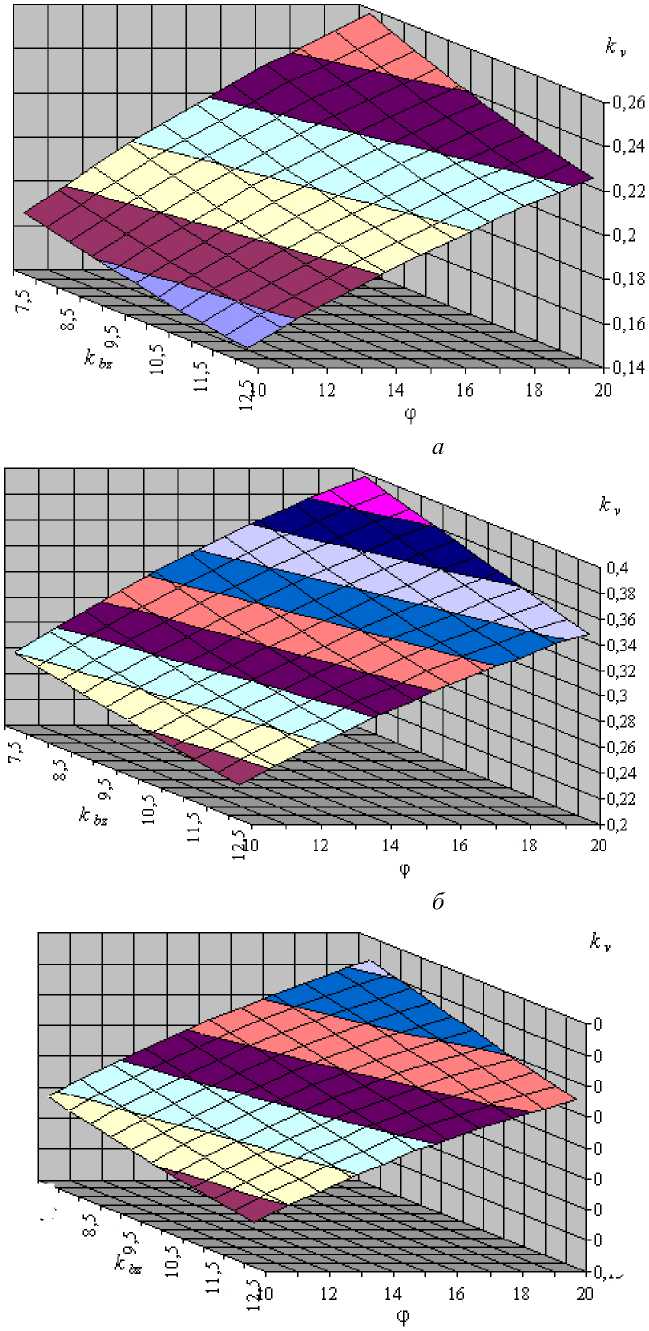
Далее для частного случая решения уравнений (9) определяется поверхность границы устойчивости течения в пространстве k_v – k_{b з} – ϕ для трех значений длин шнека n . При этом не учитывается влияние изменений величины зазора между гребнем реборды и внутренней поверхностью корпуса h _з ( х ) и глубины нарезки h ( х ) на шнеке

Построенные поверхности границы устойчивости решений в диапазонах k_{b з} =7,5…12,5 и ϕ = 10…20º представлены на рисунках 4, а , б и в для значений n = 10, 15, 20 соответственно. Выше поверхности располагается область неустойчивых решений, ниже — устойчивых. Из графиков видно, что, вне зависимости от длины шнека, изменение поверхности по k_{b з} и ϕ имеет слабо нелинейный характер, влияние величины k_{b з} проявляется сильнее на больших углах нарезки, а угла ϕ — при меньших значениях k_{b з} . С увеличением длины шнека область устойчивых решений по значению k_v несколько возрастает. Иначе говоря, уменьшение угла нарезки и относительной толщины реборды, а также уменьшение длины шнека создают условия большей чувствительности течения в экструдере к величине зазора, определяющего потоки утечек.

Таким образом, в работе предложена модель течения в канале экструдера с учетом утечек, отличающаяся тем, что течения основного потока и потока утечек

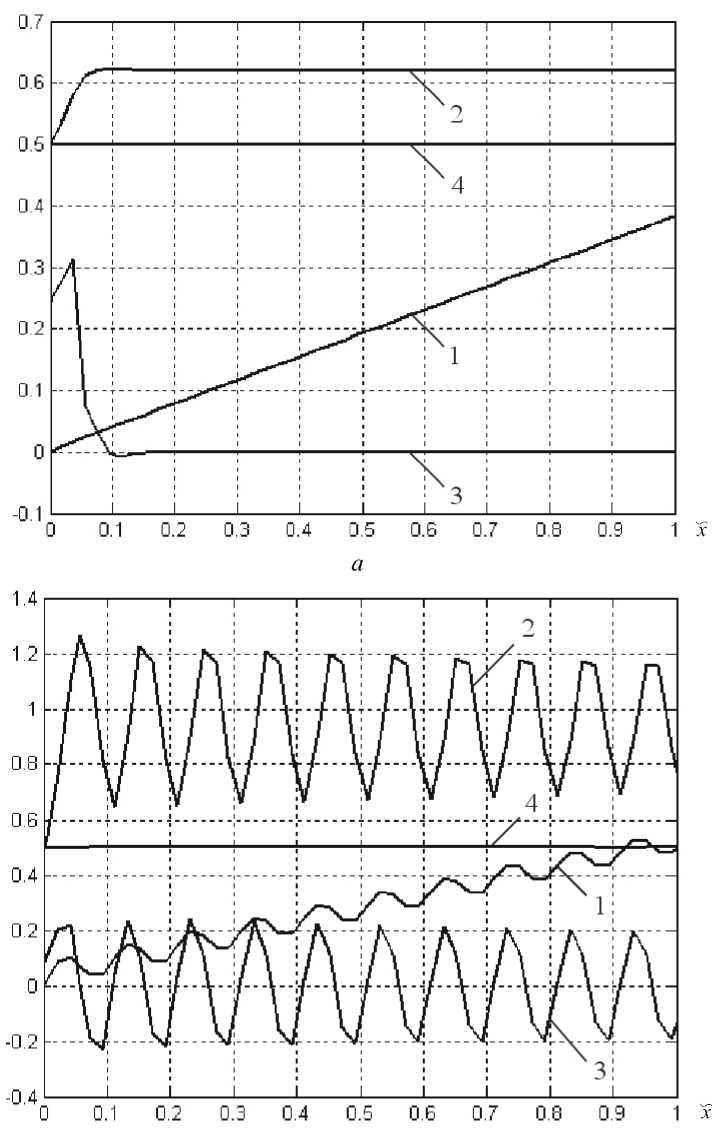
б

Рис. 3. Изменение характера течения с увеличением k_v на границе устойчивости: k_v = 0,08 ( а ) и k_v = 0,26 ( б )

рассматриваются в рамках связанной задачи: учитывается отток жидкости в канал следующего витка и приток из канала предыдущего витка, то есть учитывается возврат потока утечек в общий процесс течения материала в экструдере.

Предложенная модель дает описание общего случая течения, когда величина зазора между гребнем реборды и внутренней поверхностью корпуса h _з ( х ) и глубина нарезки h ( х ) на шнеке меняются по каналу.

7,5 J

□ 0,24-0,26

■ 0,22-0,24

□ 0,2-0,22

□ 0,18-0,2

■ 0,16-0,18

□ 0,14-0,16

• □    0,38-0,4

• ■    0,36-0,38

• □    0,34-0,36

• ■    0,32-0,34

• □    0,3-0,32

• ■    0,28-0,3

• □    0,26-0,28

• □    0,24-0,26

• ■    0,22-0,24

• □    0,2-0,22

  0,31 0,29	□ 0,29-0,31 ■ 0,27-0,29
  0,27	□ 0,25-0,27
  0,25	■ 0,23-0,25
  0,23	□ 0,21-0,23
  0,21	□ 0,19-0,21
  0,19	ПО,17-0,19
  0,17 0,15
  	□ 0,15-0,17

  
  

в

Рис. 4. Поверхность границы устойчивости течения в канале экструдера в пространстве k_v при n = 10 ( а ), n = 15 ( б ), n = 20 ( в )

-

k_bz -ϕ ,

На примере изотермического течения линейной вязкой жидкости в прямоточном шнеке с постоянными по каналу зазорами h _з и h рассмотрено влияние на вторичный поток относительной длины зазора утечек, угла нарезки шнека и длины шнека. Установлено, что в предлагаемой постановке наблюдаются существенные отличия в представлении о процессе течения в целом. Так, при выполнении в каждом сечении экструдера условия постоянства расхода, расход по каналу шнека может значительно отличаться от расхода по экструдеру в целом, при этом интенсивность притока жидкости из одного соседнего витка и оттока в другой виток не равны между собой, что в определенных условиях приводит к колебаниям интенсивности потока утечек q ( X), объемного расхода Q( X ) и давления P ( X ). С увеличением безразмерного зазора колебательный характер движения распространяется вдоль канала, и в результате решение становится неустойчивым.

Установлено, что уменьшение угла нарезки и толщины реборды, а также уменьшение длины шнека приводят к большей чувствительности течения в экструдере к величине зазора, определяющего утечки.

Указанные факторы существенно влияют на технологические характеристики экструдера и должны учитываться при проектировании и эксплуатации шнекового оборудования.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проекты № 06-08-00480 и № 07-08-97603-р_Урал_офи ) .