Модель расчета элементов каменных конструкций с коррозионными повреждениями при сейсмических воздействиях

THE MODEL FOR BRICK CONSTRUCTIONS CALCULATION DAMAGED BY CORROSION SEISMIC FORCES

The paper includes a phenomenological model for the calculation the eccentrically compressed brick buildings' elements (walls, piers, columns, etc.) with corrosion damages influenced bydynamical forces with seismic type which allows to estimate the loading capacity of constructional elements taking into account its physical and geometrical nonlinearity. Numeral realization of the model the algorithm and calculation PC program are worked out.

В настоящее время в связи с тем, что с каждой новой редакцией СНиП II-7-81 [1] повышалась расчетная сейсмичность и сотрясаемость территорий РФ, на строительных площадках с ныне расчетной сейсмичностью в 7-9 баллов присутствуют здания и сооружения с расчетной сейсмичностью в 6 баллов.

Проектирование реконструкции таких зданий и сооружений представляет весьма сложную и ответственную задачу, так как их несущая способность должна обеспечиваться при условии одновременного действия эксплуатационных и сейсмических нагрузок. Неверная оценка несущей способности элементов конструкций и здания или сооружения в целом при сейсмических воздействиях может привести к их обрушениям в короткий срок и с людскими потерями.

Нормативный расчет зданий и сооружений на сейсмические воздействия производится исходя из положений упруго деформированных элементов конструкций с введением условных эмпирических коэффициентов, учитывающих различные формы разрушения конструктивных элементов и образование пластических шарниров. Такой подход приводит к значительным отклонениям результатов расчета и проектирования от фактической работы конструкций при реальных землетрясениях и не всегда позволяет получить одновременно надежные и экономичные проектные решения.

Анализ исследований поведения зданий и сооружений при сейсмических воздействиях показывает, что их устойчивость и жесткость в целом существенно зависит от изменения прочностных и деформационных свойств материалов и реального характера деформирования основных несущих конструкций.

На конструкции, здания и сооружения в целом действует комплекс неблагоприятных факторов, в том числе и химически агрессивные загрязнения окружающей среды, вызывающие постепенное коррозионное разрушение материалов конструкций.

Разработке методов расчета и моделей деформирования различных элементов конструкций при совместном действии нагрузок и агрессивных сред посвящены исследования В.М. Бондаренко, Ю.М. Баженова, В.И. Соломатова, Е.А. Гузеева, В.И. Римшина, В.Ф. Степановой, А.М. Пухонто, Р.С. Санжаровского, И.Г. Овчинникова, В.В. Петрова, В.П. Селяева и др. И хотя в указанном направлении уже проделана определенная работа, в целом задача разработки и исследования корректных моделей деформирования и разрушения конструкций каменных зданий в химически агрессивных эксплута-ционных средах все еще весьма сложна, трудоемка и далека до окончательного решения.

В данной статье предлагается феноменологическая модель расчета внецентренно сжатых каменных конструкций (стен, простенков, столбов и т.п.) с коррозионными повреждениями при динамических воздействиях сейсмического типа.

В основу модели расчета положен подход нелинейной теории железобетона Р.С. Санжаровского [2]. При решении используется ряд теоретических предпосылок.

Расчетная схема элемента принимается в виде внецентренно сжатого стержня с шарнирно опертыми концами. Изогнутая ось стержневого элемента аппроксимируется косинусоидой. Для определения кривизны используется приближенное выражение. Считается справедливой гипотеза плоских сечений. Зависимость с т — £ для любого волокна элемента следует диаграмме с т — £ осевого сжатия кладки. В диаграммах с — £ по высоте элемента каждому значению скорости £ по высоте сечения соответствует своя кривая с — £ .

Влияние химически агрессивной среды на кирпичную кладку рассматривается как фактор, изменяющий ее деформативно-прочностные свойства. Принимается допущение о существовании границы между участком кладки с измененными свойствами и нормальным, сохранившим свои прочностные и деформативные свойства. Корродирующая и нормальная части сечения кладки связаны между собой условием совместности деформаций .

Количественной характеристикой процесса коррозии кладки является глубина проникания коррозионной среды в тело кладки:

L ( т ) = ( К ь • т ) ^m , где т - время действия коррозионной среды;

К ь , m - коэффициенты влияния агрессивности коррозионной среды на кладку.

При наличии импульсивной нагрузки дополнительно принимается, что время действия нагрузки достаточно велико по сравнению со скоростью распространения волн по длине элемента и волновые эффекты допускается не учитывать. Однократная динамическая нагрузка изменяется по произвольному закону.

Исследование параметров напряженно-деформированного состояния (НДС) элемента осуществляется для его наиболее нагруженного сечения с использованием условий равновесия. Наиболее нагруженное сечение элемента рассматривается по высоте в виде совокупности n-участков.

Рассмотрим построение модели при исследовании напряженно-деформированном состоянии каменного внецентренно-сжатого элемента, нагружаемого продольной силой. Закон изменения продольной силой в зависимости от параметра времени действия t принимаем в виде

N ( t ) = N 0 + a t .

В зависимости от значения коэффициента a , характеризующего скорость роста нагрузки на элемент, задача разделяется на две части: а) диапазон скоростей нагружения, при которых влиянием сил инерции можно пренебречь, т.е. последние не проявляются (кратковременное статическое нагружение); б) динамическое нарастающее нагружение, где влияние сил инерции существенно сказывается на движении элемента (импульсивное нагружение).

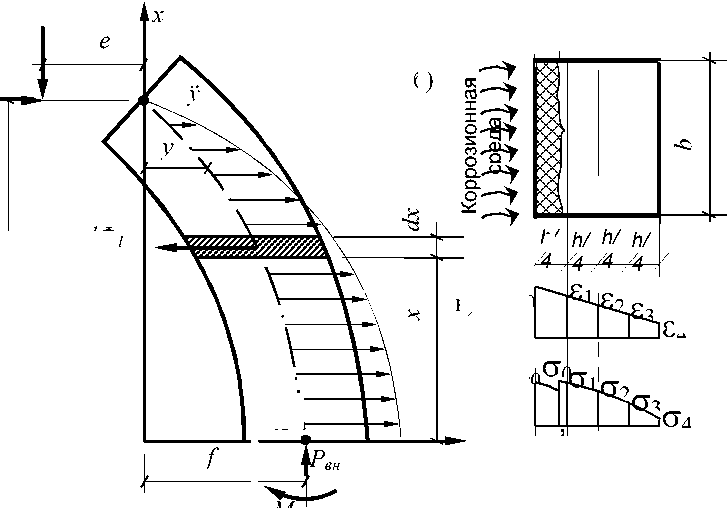
Для шарнирно опертого элемента, сжатого с равными эксцентриситетами, в качестве наиболее нагруженного можно рассматривать серидинное сечение. В этом случае расчетная схема представляется в виде, показанном на рисунке а.

Прямоугольное поперечное сечение элемента по высоте разбивается на n частей, и как показали расчеты, число разбиений 4 является наиболее оптимальным.

Гипотеза плоских сечений позволяет выразить деформации элемента на участках ( £ ) через краевые (фибровые) деформации:

n — i i — 1 ^£ i = 4 ^£ 0 ⁺ 4” " ^£ n , где i = 1 ...n — 1 .

Прогиб в рассматриваемом сечении определяется по формуле f = k " ( ^£ 0 ^{— £} n ) , где k = l 0 .

n ² "  h

Для решения задачи рассматривается часть элемента, отделенная от остальной части в наиболее нагруженном сечении. Применение принципа Германа-Эйлера-Даламбера позволяет записать уравне- ния равновесия метода кинетостатики при импульсивной нагрузке для отделенной части стержня, поэтому, согласно рисунку а, получаем

N ( t ) - Р вн = 0; Q = Р ф1 = 0;

N(t)(e + f )- M ф1 - M вн = 0, где Pф1 – главный вектор поперечных сил инерции, действующих на отсеченную половину стержня;

М _{ф 1} – главный момент сил инерции;

P _вн – главный вектор внутренних нормальных усилий;

М _вн – главный момент внутренних нормальных усилий.

Значение элементарной силы инерции, действующей на отрезок стержня длиной dx (рис. 1а), определяется выражением dФ1 = yyFdx, где у - плотность кирпичной кладки;

F – площадь поперечного сечения элемента.

Интегрируя (1) по длине с учетом приближенного выражения для кривизны находим l 2

Q = Р ф 1 = F F yC cos n x dx = Fl f ^;

0           l l22

n • x          l F y l ■■

M ф 1 = J F y fcos—xdx - ^Q- = —2~ f ^.

0          l2

Величины главного вектора P_вн и главного момента М _вн находим из эпюры нормальных напряжений и относительных деформаций в среднем сечении.

Система дифференциальных уравнений движения элемента имеет вид:

4(5)

С l ^ O ⁺ С 2 ^ 4 + С 3< & 0 + С 4 <7 1 = С 5 ;

c 6 ^ 0 + С 7 ^ 4 = С 8 ;

' c 9 § 0 + c 10 7 0 = С 11 ;

_ С 12 § 0 ⁺ С 13 § 4 ⁺ С 14 ⁷ 1 = С 15 •

а) N(t)

Q

б)

h/ dФ1

£ c

G er I

Q сr

y вн

б

A

в)

Рис. Схема усилий, действующих на отсеченную часть элемента (а); поперечное сечение элемента после одностороннего воздействия в течение времени т коррозионной среды (б); распределение деформаций и напряжений по высоте сечения элемента (в)

Система уравнений (2) приводится к нормальному виду:

^ о = x i ;

[⁽ C 5 С ю ^— C 3 C 11 ) C 14 ^— C 4 C io C 15 ] C 7 C 10 C 14 ^—

X =      ^{— (} C 2 C 10 C 14 ^— C 4 C 10 C 13 ) C 8 C 10 C 14      , ;

• ¹   [⁽ C 1 C 10 ^— C 3 C 9 ) C 14 ^— C 4 C 10 C 12 ] C 7 C 10 C 14 ^—

• ^{— (} C 2 C 10 C 14 ^— C 4 C 10 C 13 ) C 6 C 10 C 14      ,

• - 4 = x 2 ;

^{[ ( C} 5 ^C 10 - ^C 3 ^C 11 ^{) C} 14 - ^C 4 ^C 10 ^C 15 ] ^C 6 ^C 10 ^C 14 ^—

X = ^{— [} C 14 ^{( C} 1 ^C 10 ^{— C} 3 ^C 9 ^{) — C} 4 ^C 10 ^C 12 ] ^C 8 ^C 10 ^C 14 ;

• ^{2       ( C} 2 ^C 10 ^C 14 ^{- C} 4 ^C 10 ^C 13 ^{) C} 6 ^C 10 ^C 14 ^-

• - [C14(C 1C10 - C3C9 ) — C4C10C12]C7C10C14

• ^T 0 = x 3 ;

^{[ ( C} 5 ^C 10 ^{- C} 3 ^C 11 ^{) C} 14 ^{- C} 4 ^C 10 ^C 15 ] ^C 7 ^C 10 ^C 14 ^-

^C 11 _— ^C 9 _<      ^{-( C} 2 ^C 10 ^C 14 ^{- C} 4 ^C 10 ^C 13 ) ^C 8 ^C 10 ^C 14

^C 10   ^C 10   ^{[ C} 14 ^{( C} 1 ^C 10 ^{- C} 3 ^C 9 ^{) — C} 4 ^C 10 ^C 12 ] ^C 7 ^C 10 ^C 14 ^-

_      ^{-( C} 2 ^C 10 ^C 14 ^{- C} 4 ^C 10 ^C 13 ) ^C 6 ^C 10 ^C 14     .

•                            .

T 1 = X 4 ;

[ ⁽ C 5 C 10 ^- C 3 C 11 ) C 14 ^- C 4 C 10 C 15 ^] C 6 C 10 C 14 ^- C 15 - C 13 . ^- [ C 14 ⁽ C 1 C 10 ^- C 3 C 9 ^)- C 4 C 10 C 12 ^] C 8 C 10 C 14 C 14 C 14 ⁽ C 2 C 10 C 14 ^- C 4 C 10 C 13 ) C 6 C 10 C 14 ^-

—

^ ^{- [} C 14 ⁽ C 1 C 10 ^- C 3 C 9 ^)- C 4 C 10 C 12 ^] C 7 C 10 C 1414 .

C 12

C 14

^{[ (} C 5 C 10 ^— C 3 C 11 ) C 14 ^— C 4 C 10 C 15 ^] C 7 C 10 C 14 ^{— — (} C 2 C 10 C 14 ^— C 4 C 10 C 13 ) C 8 C 10 C 14

^[ C 14 ⁽ C 1 C 10 ^— C 3 C 9 ^)— C 4 C 10 C 12 ^] C 7 C 10 C 14 ^{— — (} C 2 C 10 C 14 ^— C 4 C 10 C 13 ) C 6 C 10 C 14

Начальные условия для решения вышеприведенной системы уравнений определяются из расчета стержня на нагрузку N ₀ . В качестве критерия потери устойчивости элемента используется равенство вариаций моментов внешних и внутренних сил (при условии равенства нулю вариации продольной силы).

Приравнивая нулю определитель системы, составленный из коэффициентов при вариациях, получают функционал потери устойчивости.

Таким образом, поставленная задача распадается на две части:

• 1)    определение кинематических уравнений движения;

• 2)    проверка условия критического состояния.

Первая часть задачи реализуется на ЭВМ. Одновременно просчитывается функционал потери устойчивости (вторая часть задачи).

Если в какой-то момент t * функционал обращается в нуль, то этот момент является в данной ситуации критическим временем. Так как функция N = N ( t ) задается, то, подставляя в нее значение t * , получают продольную силу в момент исчерпания несущей способности стержня.

Построение расчетной модели элемента с коррозионными повреждениями при воздействии динамической нагрузки осуществляется следующим образом. Коррозионная среда действует на элемент в течение времени т (рис. б). Влияние среды проявляется в изменении физико-механических свойств кирпичной кладки по периметру сечения элемента на глубину L ( т ) . Поперечное сечение элемента представляется состоящим из двух участков с разными физико-механическими характеристиками: участка кладки без коррозионных повреждений и участка кладки с коррозионными повреждениями.

Главный вектор Р _вн и главный момент М _вн определяются из эпюры распределения напряжений и деформаций в среднем сечении (рис. в) и описываются выражениями

Р вн ( т ) = Р Вн ( т ) = P ^b ( т ) + 2 Р СГн ( т ) ;

Mни ( т ) = М н ( т ) = M ^b ( т ) + 2 M^e _cr ( т )

Система дифференциальных уравнений движения элемента с коррозионными повреждениями имеет вид:

*

*

*

*

*

С 1 $ & 0 + С 2 $ & 4 + С 3 7 + С 4 7 = С 5 ;

*

*

*

«

С 6 ё 0 + С 7 ё 4 = С 8 ;

*

*

*

^С 9 ^е 0 ^{+ С} 10 ⁷ 0 = ^С 11 ^;

*

*

*

*

[ С 12 ё 0 + С 13 ё 4 + С 14 ^ 1 = С 15 .

Коэффициенты при неизвестных в (3) имеют следующие значения: 22

* bh    ^£ 0^£ 4 ⁺ е • „ * bh    ^е 0 ^е 4 ^{+ е} 0 •

С = m -^; С = <7 1:г^;

1 ² 1 ( е 0 + е 4 ) ^{3      2        2} 1 ( е 0 + е 4 ) ³

* bh .     * bh ^f

^{С 3} = T ^{С 4} = TI ^{1 +}

З е о

£ 4 ] ;

^£ о ⁺ е 4

*

С 5 =— bh < o "1

с 6 = 1 ; с ₇ = 1 ;

* *

^С 10 =^{— 1;} C 11

C ₁₃ * = 0 , 5 A ₂ * ( 0 , 75 е ₀

^е 0 ^е 4 ^{( е} 0 ^{— е} 4 ^{)+( е} 0 ^е 4 ^{— ( е} 0 ^{+ е} 4 ^{) 3}

^е 4 8 2 )

⁺<& 1

^£ 4 ^е 0

—

^£ 0 ^е 4

_ ^{( е} 0 + ^е 4 ^{) 2}

;

*

С 8 =

= ( 0 , 25 ^ ( t ) l — M_№ ) n ² _;

( F c_r + F h W l

= 2 A 2 е ^ , C 12

*    ___ *

= 0 , 75 A 1

—

C 9 = A 1

—

² A 2 ^£ 0 ;

— 1 , 5 A ₂ * ( 0 , 75 е ₀ — 0 ,25 е ₄ ) ’

0 , 25 е ₄ ) — 0 , 25 A1* ’ С ₁₄ * =— 1 ’ C ₁₅ * = 2 A ₂ * ( 0 ,15 е ₀ — 0 ,25 е 4 ) ² .

Далее система уравнений (3) приводится к нормальному виду и решается на ЭВМ как задача Коши методом Рунге-Кутта.

Модель расчета реализована в пакете прикладных программ «PARKK», ориентированном на ПЭВМ IBM PC/AT на базе процессора Intel-80286 со стандартным техническим обеспечением. Экспериментальным путем получены прочностные и деформативные зависимости при повторных нагружениях кирпичной кладки с коррозионными повреждениями в хлорсодержащих и сульфатных средах, а также опытные данные об особенностях деформирования и разрушения при повторяющихся нагружениях кирпичных столбов и простенков с коррозионными повреждениями. Выполнен сравнительный анализ экспериментальных результатов с результатами расчета по предложенной методике. Сравнение показало адекватность разработанной феноменологической модели расчета, позволяющей получить достаточно близкие к действительным значениям результаты.