Модель расчета текущих размеров обрабатываемой поверхности при шлифовании некруглой заготовки в цикле круглого врезного шлифования с ЧПУ
Автор: Акинцева Александра Викторовна, Переверзев Павел Петрович
Рубрика: Численные методы моделирования
Статья в выпуске: 2 т.21, 2021 года.
Бесплатный доступ
На данный момент среди большого количества различных CAM-систем отсутствует цифровой инструмент контроля проектируемых управляющих программ для станков с ЧПУ, позволяющий проверить возможность обеспечения точности и шероховатости обрабатываемой поверхности при изготовлении партии деталей. В результате проектируемые при помощи данных CAD/CAM-систем управляющие программы требуют проведения процедуры проверки в реальных производственных условиях при помощи обработки ряда пробных деталей. Не смотря на всю точность систем позирования современные шлифовальные станки с ЧПУ, позволяющие вести обработку по заданным циклам режимов резания, имеют упругие деформации технологической системы. Они оказывают значительное влияние на колебания величины снимаемого припуска и на образование погрешностей размеров при изготовлении партии деталей. Обработка партии деталей производится в переменных технологически условиях; примерно 90 % погрешности обработки объясняется колебанием радиуса детали, вызванным исходным радиальным биением заготовки и колебанием припуска. Это и обуславливает необходимость установления функциональной взаимосвязи между колебанием размеров обрабатываемой поверхности заготовки с выходными, входными и управляющими параметрами цикла с учетом колебания припуска и исходного радиального биения заготовки на протяжении всего процесса обработки. В данной статье представлено описание модели расчета текущих размеров обрабатываемой поверхности при шлифовании некруглой заготовки в цикле круглого врезного шлифования с ЧПУ. Модель позволяет рассчитывать изменения фактической радиальной подачи на каждом радиусе обрабатываемой поверхности на каждом обороте заготовки в течение всего цикла шлифования с учетом исходного радиального биения заготовки. Это дает возможность рассчитать изменения текущих размеров обрабатываемой поверхности на протяжении всего цикла, учитывая «наследственную форму» заготовки. Данная модель может применяться не только для прогнозирования точности диаметральных размеров и отклонения и расположения формы поверхностной, но и для оптимизации циклов круглого врезного шлифования.
Круглое шлифование, цикл, модель расчета глубины резания, прогнозирование точности обработки
Короткий адрес: https://sciup.org/147233505
IDR: 147233505 | УДК: 621.923.9 | DOI: 10.14529/engin210205
Текст научной статьи Модель расчета текущих размеров обрабатываемой поверхности при шлифовании некруглой заготовки в цикле круглого врезного шлифования с ЧПУ
В настоящий момент в связи с переходом на цифровое производство все более остро встает вопрос разработки инструмента, позволяющего контролировать управляющие программы для станков с ЧПУ (УП) на возможность обеспечения точности и шероховатости обрабатываемой поверхности при изготовлении партии деталей. Имеющиеся на предприятиях различные CAD/CAM-системы, созданные для автоматизированного проектирования операций механической обработки, не содержат в своем арсенале инструмента для контроля cпроектированных УП. К тому же подавляющая часть CAD/CAM-систем при разработке УП в части назначения циклов режимов резания использует усредненную заниженную статистику, не учитывающую количественное влияние большого числа переменных технологических факторов. В результате разработанные при помощи данных CAD/CAM-систем УП требуют адаптации к реальным производст- венным условиям при помощи обработки ряда пробных деталей. Это влечет за собой дополнительные материальные, временные и трудовые затраты.
Окончательные размеры обрабатываемых поверхностей точных деталей большей частью получаются на шлифовальных операциях, к которым предъявляются «жесткие» требования по точности обработки – квалитет 6–7 и шероховатость по Ra 0,05…1,6. Помимо допуска диаметрального размера, на операциях круглого шлифования задаются допуски формы и расположения поверхностей, которые ужесточают требования к точности обработки. В процессе шлифования окончательные размеры обрабатываемой поверхности формируются в результате многократного съема слоя металла в течение всего цикла шлифования и определяются большим количеством технологических факторов. Вопрос прогнозирования точности обрабатываемой поверхности заготовки при шлифовании партии деталей является актуальным, поэтому возникает необходимость в установлении взаимосвязи, отражающей изменения текущих размеров заготовки на протяжении всего процесса обработки.
Обработка на станках с ЧПУ и управление циклами режимов резания осуществляется при помощи прибора активного контроля (ПАК), который предназначен для непрерывного измерения текущего обрабатываемого размера заготовки. По его командам производится отвод, подвод круга и переключение программной радиальной подачи (цикл радиальной подачи) в зависимости от оставшейся части припуска. На производстве принято настраивать ПАК на середину поля допуска детали (рис. 1). ПАК имеет низкую погрешность – до 1 мкм. В результате можно предположить, что 90 % погрешности обработки обусловлено колебанием радиуса детали, вызванным исходным радиальным биением заготовки.
ПАК устанавливает и контролирует диаметральные размеры заготовки только в данном сечении, которое имеет минимальный размер в «наследственном эллипсе». Контроль всей формы детали не осуществляется, поэтому возникает рассеивание всех остальных диаметральных размеров вокруг диаметра, который контролируется ПАКом. Несмотря на то, что ПАК с высокой точностью производит отвод круга, наследственное радиальное биение может оказаться больше поля допуска требуемой точности обработки. Для снижения радиального биения (оно должно быть равным величине или меньше величины допуска диаметра готовой детали) необходимо снизить скорость фактической радиальной подачи. Поэтому возникает необходимость установления функциональных взаимосвязей между колебанием размеров обрабатываемой поверхности заготовки с выходными, входными и управляющими параметрами цикла (физико-механическими свойствами обрабатываемого материала, степенью затупления и характеристикой круга и др.) с учетом колебания припуска и исходного радиального биения заготовки на протяжении всего процесса обработки.
Прогнозирование точности обработки, ввиду актуальности вопроса, в разное время, рассматривалось как в отечественных работах [1–6], так и зарубежных [7–14]. Большая часть из них направлена на лезвийную обработку [1–12], а для абразивной обработки по большей части прогнозирование точности осуществлялось только в направлении моделирования получаемой шероховатости и волнистости обрабатываемой поверхности [15–18]. В небольшом количестве работ рассмотрено моделирование и прогнозирование точности шлифования [4–6, 13,14]. Общим недостатком данных работ является то, что в них рассматривается обработка «идеальных поверхностей» (абсолютно круглые или плоские поверхности) без учета упругих деформаций технологической системы. В результате проведенного анализа можно сказать, что прогнозирование точности обработки на операциях шлифования является сложной и до сих пор полностью не решенной научной задачей. Суть задачи прогнозирования точности обработки заключается в том, что для партии изготовленных деталей необходимо предсказать, будут ли в пределах заданного допуска для всех деталей в партии погрешности диаметрального размера, отклонения формы (круглости, цилиндричности), отклонения суммарного допуска формы и расположения (радиального биения, полного радиального биения), с учетом переменных условий обработки (затупление и износ круга, колебание припуска и исходным радиальным биением заготовки) для заданных условий шлифования. К заданным условиям относятся материал детали, переменная податливость технологической системы по длине обрабатываемой поверхности, характеристики круга, точность диаметра заготовки, припуск на обработку, режимы резания и др.
В качестве решения данной задачи предложена аналитическая модель расчета текущих размеров обрабатываемой поверхности при шлифовании некруглой заготовки в цикле круглого врезного шлифования с ЧПУ. Данная модель позволяет рассчитывать величину снимаемого припуска на каждом радиусе обрабатываемой поверхности заготовки на протяжении всего цикла шлифования, т.е. на каждом обороте заготовки на z -ой ступени цикла. В результате становится возможным рассчитать изменения текущих размеров обрабатываемой поверхности на протяжении всего цикла шлифования при ступенчатом изменении программной подачи с учетом колебаний припуска и исходного радиального биения заготовки. Рассмотрим основные этапы разработки аналитической модели расчета текущих размеров обрабатываемой поверхности при шлифовании некруглой заготовки в цикле круглого врезного шлифования с ЧПУ.
Примем модель поверхности некруглой заготовки в виде эллипса (рис. 1), который охватывает поле допуска заготовки и учитывает ее исходное радиальное биение. По самому неблагоприятному сценарию обработки исходное радиальное биение примем равным ½ поля допуска диаметра заготовки. В результате форма готовой детали примет форму эллипса с меньшим радиальным биением, так как будет наблюдаться меньшая разница полуосей эллипса. Профиль заготовки в виде эллипса характеризуется разной длиной радиусов, изменяющихся в пределах допус- ка диаметрального размера, и описывается следующими известными уравнениями:
X- + У- = 1 a 2 b 2 ,
ab
Г = I ==
/,2 2 ,2-2 ’
5/b cos ф + a sin ф a = 0,5d
, заг _max ,
b = 0,5 d 3ar
min ,
где a и b – длина наибольшей и наименьшей полуоси эллипса, мм; r – текущий радиус эллипса в зависимости от угла φ поворота радиуса, мм; d заг _max , d заг _min – максимальный и минимальный диаметр заготовки соответственно, мм; φ – угол поворота радиуса r , град.
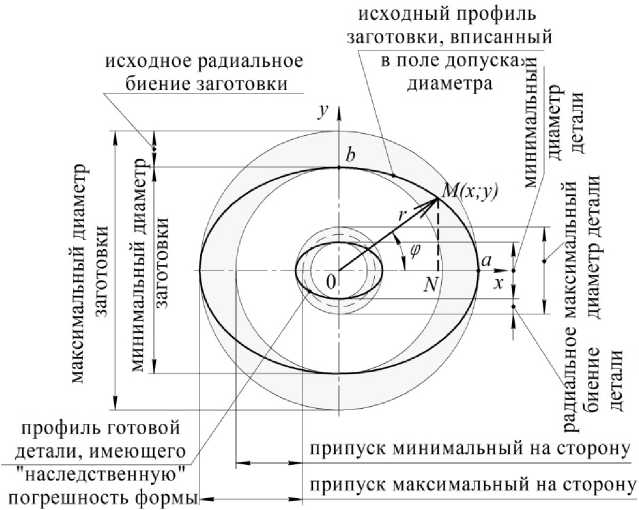
Рис. 1. Расчетная схема припусков и параметров поверхностей заготовки и детали
Рассмотрим съем припуска с некруглой заготовки, имеющей форму эллипса, в процессе круглого наружного врезного шлифования. В начале процесса съема припуска происходит прерывистое резание в течение времени ^тпрер. Во время прерывистого резания происходит удаление металла с вершин эллипса, имеющих максимальное значение радиуса. При этом изменение скорости фактической радиальной подачи происходит от нуля при «шлифовании воздуха» до максимального значения, определяемого упругими деформациями технологической системы, радиальной составляющей силы резанья, величины натяга и др. условий обработки. После завершения этапа прерывистого резания скорость фактической радиальной подачи колеблется на каждом радиусе обрабатываемой поверхности заготовки с амплитудой АSФ до минимального значения в конце цикла шлифования. Данные колебания АSФ соответствуют колебаниям упругой деформации технологической системы и радиальной составляющей силы резания. В результате можно сказать, что чем больше колебания радиуса обрабатываемой поверхности заготовки, тем больше величина колебаний амплитуды АSФ.
При описании эллипсной заготовки четырьмя радиусами (рис. 2, а), радиусы номер 1 и 3 имеют максимальное значение, а радиусы номер 2 и 4 – минимальное значение. Обозначим номер радиуса через b , номер оборота заготовки в процессе шлифования через i, а порядковый номер ступени цикла через z . Тогда номера радиусов заготовки обозначим, как R z,i,b . Исходные радиусы заготовки перед шлифованием обозначим при i = 0 и z = 1, как R 1,0, b . Максимальный радиус заготовки R заг max равен половине максимального диаметра заготовки d заг max – формула (5), а минимальный радиус заготовки – формула (6).
R
заг
= 0,5 d max , заг
max
R заг
= 0,5 d min , заг
min ,
где R заг _max(min) – максимальный (минимальный) радиус заготовки, мм.
Тогда для эллипсной заготовки при i = 0 и z = 1: R 1,0,1 = ^ 1-0,3 = R3ar_max и R102 = R 1,0,4 = R3ar _™n .
Колебание радиусов Δ R загb поверхности заготовки равно разнице между максимальным радиусом заготовки и b -ым радиусом, т. е.
A R загЬ = R _max — R^ b , (7)
где АКзагЬ - радиальное биение заготовки, мм; Rz,i,b - текущий размер Ь-ого радиуса обрабатывае- мой поверхности заготовки на i-ом обороте z-ой ступени, мм; b – порядковый номер радиуса обрабатываемой поверхности заготовки; z – порядковый номер ступени цикла; i – порядковый номер оборота заготовки.
Тогда для эллипсной заготовки
Δ R заг 1
= Δ R заг 3
Δ R заг 2
= Δ R заг 4
R заг_max – R 1,1,0
R заг_ma x
– R 1,2,0
R заг_max – R 1,3,0
R заг_max
– R 2,4,0
R заг_max
R заг_max
R заг_max
= 0,
R заг_min .
Графики фактических подач одновременно являются графиками текущих значений радиусов
заготовки. Зигзагообразный характер графиков фактических подач обусловлен исходным колебанием радиусов заготовки, наследственно передающихся на каждом обороте заготовки в течение всего цикла шлифования. Траектория исходных радиусов заготовки показана на прерывистом участке резания (рис. 3). Нечетные радиусы (1 и 3) имеют максимальные значения и касаются оси абсцисс, четные радиусы (2 и 4) – минимальные значения и расположены от оси на расстоянии радиального биения Δ R загb . На первых оборотах заготовки, пока радиусы 2 и 4 находятся выше графика накопленных подач t Пz,i,b , т. е. радиусы 2 и 4 не касаются шлифовального круга и между ними образовался зазор y з .
Таким образом, из графика на рис. 3 следует, что радиусы эллипсной заготовки изменяются от максимального значения до минимального в пределах исходного радиального биения заготовки Δ R загb . Поэтому в самом начале цикла, шлифование ведется в режиме прерывистого резания, когда между кругом и заготовкой образуется зазор y з (рис. 2, б) между радиусом заготовки и поверхностью круга из-за колебания размеров радиусов заготовки. На этапе прерывистого резания съема металла не происходит, а происходит «шлифование воздуха». Поэтому фактические пода-
чи и сила резания равны нулю.
Рассмотрим математическое условие возникновения зазора на этапе прерывистого резания. На этапе врезания между кругом и эллипсной заготовкой образуется зазор y з (см. рис. 2, б), так как программная накопленная подача t Пz,i,b не достигает на первых оборотах минимального радиуса 2 (или 4) заготовки из-за ее некруглости, при которой радиус R 1,0,2 < R 1 , 0,1 .
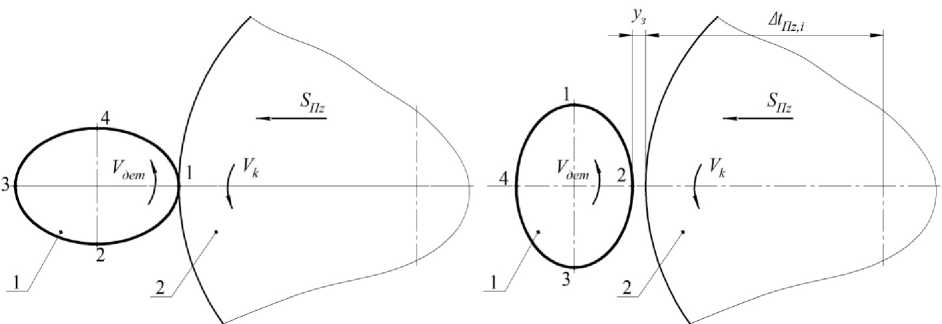
Рис. 2. Нумерация радиусов заготовки (1 – заготовка; 2 – шлифовальный круг): начало процесса шлифования с момента касания круга наибольшим радиусом 1 эллипсной заготовки (а); зазор между кругом и наименьшим радиусом 2 эллипсной заготовки (б)
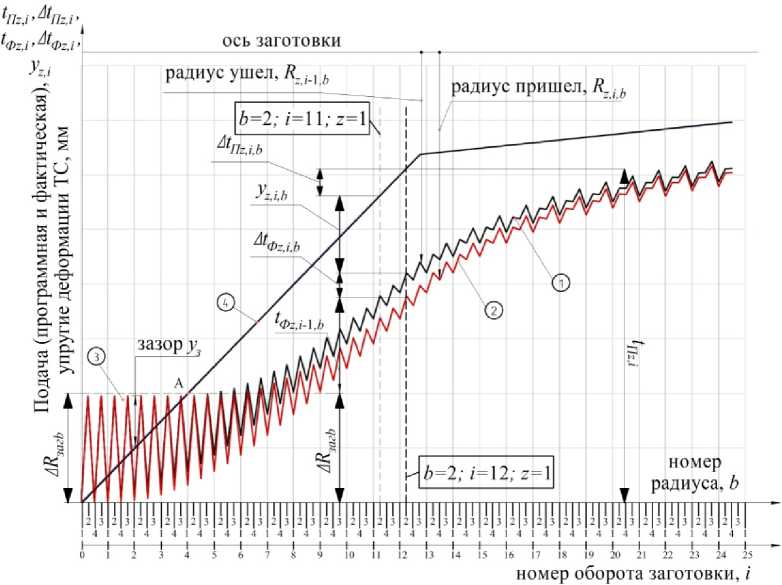
Рис. 3. График подач при съеме металла с некруглой заготовки: 1 – траектория радиуса заготовки и фактической подачи на i- м обороте; 2 - траектория радиуса заготовки и фактической подачи на i- 1 обороте; 3 – зона прерывистого резания; 4 – программная траектория шлифовального круга t Пz,i ;
Величину зазора y з можно определить как разницу между радиальным биением заготовки Δ R загb и накопленной программной подачей, по формуле (10) или после подстановки уравнения (9) – по формуле (11).
yз =Δ Rзагb - tПz , i , b ≥ 0, (10)
y з = R заг _max - t Пz , i , b ≥ 0, (11) где y з – величина зазора между кругом и заготовкой на этапе прерывистого резания, мм; t Пz,i,b – программная накопленная радиальная подача, мм.
Процесс прерывистого резания идет до точки А (см. рис. 3), пока Δ R загb ≥ t Пz , i , b . В точке A (см. рис. 3) пересекаются графики накопленных программных и фактических подач. Поскольку t Пz,i,b увеличивается с каждым оборотом заготовки, то после точки А значение tп z,i,b станет больше
Δ R загb , и этап прерывистого резания закончится, а значение зазора y з , вычисленное по формуле (10), станет отрицательным.
Для вывода формулы расчета текущего значения скорости фактической подачи t Фz,i,b в цикле шлифования рассмотрим размерную цепочку (выделена на рис. 3 утолщенными стрелками) подач, упругих перемещений и колебания радиуса заготовки. Баланс цепочки построен для момента (штриховая линия на рис. 3) съема металла с радиуса b = 2 после оборота i = 12 заготовки.
Как видно из построения на рис. 3, размерная цепь состоит из баланса следующих перемещений tnz, i, b = yz, i, b + ^Ф, i, b + tФz, i-1, b + R3arb ,
yz , i , b = Y P Yz , i , b ,
PYz,i,b = K3^tOz,i,b + K4 V^t®z,i,b , tП(Ф)z,i,b
ZI
= TL ^ t nwi„,
z = 1 i = 1
K 3 = n dBn g ^ i ^ i !g e , (16)
к
g I dD
K 4 = n B lt^T^ , (17)
3 Nd + D где yz,i,b – упругая деформация технологической системы, которая находится по формуле (13), мм; γ – податливость технологической системы, мм/Н; PУz,i,b – радиальная составляющая силы резания на i-ом обороте детали z-й ступени цикла, Н (более подробно с моделью силы резания можно познакомиться в статье [19]); ΔtПz,i,b (ΔtФz,i,b) – программная (фактическая) скорость подачи шлифовального круга за оборот детали, мм/об; tПz,i,b (tФz,i,b) – накопленное значение программной (фактической) скорости подачи на i-ом обороте z-ой ступени, которая находится по формуле (15), мм; I – максимальное количество оборотов заготовки; Z – максимальное количество ступеней цикла; σi – интенсивность напряжений в движущемся объеме металла, характеризующая сопротивление металла пластической деформации при степени, скорости деформации и температуре, присущих процессу шлифования, Н/мм2 ; К3, К4 – коэффициенты, находящиеся по формулам (16) и (17); εi – интенсивность скорости деформации объема металла в зоне сдвига, 1/с; β – угол между вектором RSj и вектором окружной скорости вращения шлифовального круга Vk, град; В – ширина геометрической зоны контакта круга с деталью – это часть высоты круга, равная длине обрабатываемой поверхности заготовки, мм; D – диаметр шлифовального круга, мм; d – диаметр обрабатываемой поверхности детали, мм; η – степень затупления шлифовального круга, равная отношению суммарной площади площадок затупления всех зерен круга, находящихся на всей его поверхности, к геометрической площади всей рабочей поверхности круга, т. е. величина η определяет относительную опорную поверхность круга по площадкам затупления зерен; Vk – окружная скорость вращения круга, м/с.
Рассмотрим особенности расчета параметра Δ R загb в уравнении (12). Для максимальных радиусов 1 и 3 эллипсной заготовки значение Δ R загb = 0, а для минимальных радиусов 2 и 4 значение Δ R загb = R заг_max – R z,i,b > 0. Физически это означает, что радиусы 2 и 4 войдут в контакт с кругом не на первом обороте, а через несколько оборотов, после точки А (см. рис. 3). Поэтому точка отсчета накопленной программной подачи для радиусов 2 и 4 сдвигается, по сравнению с радиусами 1 и 3, для которых отсчет накопленной подачи начинается с первого оборота заготовки.
Вследствие этого для максимальных и минимальных радиусов уравнение (12) можно записать следующим образом. Для максимальных радиусов 1 и 3 при Δ R загb = 0
t nz , i , b = yz , i , b + ^ tФz , i , b + tФz , i - 1, b . (18)
Для минимальных радиусов 2 и 4:
-
– в зоне прерывистого резания до точки А (см. рис. 3), при y з = Δ R загb – t Пz,b,i ≥ 0, когда радиусы 2 и 4 не шлифуются: tnzib = 0 .
-
– в зоне сплошного резания после точки А и при y з < 0, расчет ведется по уравнению (12).
Для получения формулы, необходимой для расчета текущего значения скорости фактической подачи ∆ t Фz,i,b , выполним подстановку и преобразование уравнения (12) и решим относительно ∆ t Фz,i,b в следующем виде
^ tФz , i , b
Y K 4 + t nz , i , b tФz , i - 1, b ^ R 3arb
2(1 + K 3 Y ) J 1 + K 3 Y
γK 4
2(1 + K 3 Y )
Расчет ∆ t Фz,i,b ведется при следующих начальных условиях: начиная с первого оборота заготовки при i = 1: t nz 1 b = ^ t n z 1 b и t Фz 0 b = 0. Уравнение (19) решается по-разному для максимальных и минимальных радиусов. Для максимальных радиусов при b = 1 и b = 3 значение Δ R загb = 0.
Для минимальных радиусов при b = 2 и b = 4 при шлифовании в зоне прерывистого резания значение ∆ t Фz,i,b = 0. А при шлифовании в зоне сплошного резания значение ∆ t Фz,i,b рассчитывается по уравнению (19).
Важной особенностью расчета параметров цикла шлифования некруглой заготовки является необходимость учета исходного радиального биения заготовки при назначении снимаемой части припуска на первой ступени. Поскольку ПАК нельзя включать когда шлифование ведется в зоне прерывистого резания то и припуск на сторону П 1 на первой ступени цикла должен быть гарантированно больше радиального биения заготовки т. е. П 1 > R заг _ max .
Таким образом аналитическая зависимость (19) представляет собой функциональную взаимосвязь между параметрами точности обработки радиальной составляющей силы резания режимами резания упругой деформацией технологической системы временем цикла и другими основными технологическими факторами которые включают в себя физико-механические свойства шлифуемого металла геометрические параметры зоны контакта круга и заготовки (фактическая скорость подачи диаметры заготовки и круга частота вращения заготовки ширина обрабатываемой поверхности заготовки) характеристику шлифовального круга и степень затупления зерен круга. При этом учитываются колебания припуска и радиального биения заготовки при изготовлении партии деталей.
Выводы
-
1. Растущие темпы оснащения машиностроительного производства современными станками с ЧПУ позволяющими вести обработку по заданным циклам управления режимными параметрами выявили отсутствие «работающего» цифрового инструмента для создания и контроля УП. Данные УП должны гарантировать стабильность показателей точности и качества при обработке партии детали без дополнительных затрат на адаптацию к реальным производственным условиям. В результате возникла необходимость разработки цифровой модели съема припуска отражающей изменения текущих размеров заготовки по всей длине обрабатываемой поверхности и на протяжении всего процесса обработки с учетом колебаний припуска и исходного радиального биения заготовки.
-
2. Несмотря на всю точность систем позирования современные шлифовальные станки с ЧПУ позволяющие вести обработку по заданным циклам режимов резания имеют упругие деформации технологической системы. Они оказывают значительное влияние на колебания величины снимаемого припуска и на образование погрешностей размеров при изготовлении партии деталей. Обработка партии деталей производится в переменных технологических условиях в том числе с учетом колебаний припуска и исходного радиального биения заготовки. Примерно 90 % погрешности обработки обусловлено колебанием радиуса детали вызванного колебанием припуска и исходным радиальным биением заготовки.
-
3. В качестве решения данной задачи предложена аналитическая модель расчета текущих размеров обрабатываемой поверхности при шлифовании некруглой заготовки в цикле круглого врезного шлифования с ЧПУ. Это становится возможным благодаря многократному моделированию процесса съема припуска на каждом обороте заготовки в течение всего цикла шлифования. В результате можно рассчитать изменения текущих размеров обрабатываемой поверхности на протяжении всего цикла шлифования при ступенчатом изменении программной подачи с учетом колебаний припуска и исходного радиального биения заготовки. Данная аналитическая модель
послужит основой цифровой модели процесса шлифования, которая позволит не только прогнозировать точность обработки, но и проводить оптимизацию цикла шлифования, гарантирующего стабильность показателей точности и качества при обработке партии деталей [20].
Исследование выполнено при финансовой поддержке РФФИ и Челябинской области в рамках научного проекта № 20-48-740006.
Список литературы Модель расчета текущих размеров обрабатываемой поверхности при шлифовании некруглой заготовки в цикле круглого врезного шлифования с ЧПУ
- Кондрашов, А.Г. Прогнозирование точности при обработке резанием / А.Г. Кондрашов, Д.Т. Сафаров // Известия высших учебных заведений. Сер. «Машиностроение». – 2014. – № 12. – С. 63–69.
- Жолобов, А.А. Прогнозирование и обеспечение точности токарной обработки ступенчатых валов / А.А. Жолобов, А.В. Казаков // Вестник Белорусско-российского ун-та. – 2014. – № 1(42). – С. 6–14.
- Волчкевич, И.Л. Прогнозирование ожидаемой точности при механической обработке партий деталей / И.Л. Волчкевич // Известия Тульского гос. ун-та. Сер. «Технические науки». – 2011. – № 6(2). – С. 3–9.
- Ломова, О.С. Исследование точности процесса круглого шлифования имитационным моделированием / О.С. Ломова, И.А. Сорокина // Омский научный вестник. – 2013. – № 2(120). – С. 99–102.
- Анализ формы шлифованных поверхностей при круглом шлифовании / С.М. Братан, С.И. Рощупкин, Д.Е. Сидоров, П.А. Новиков // Ученые записки Крымского инженерно-педагогического университета. – 2020. – № 1(67). – 259–262.
- Никитин, С.П. Влияние колебаний динамической системы станка на точность и температуру при шлифовании / С.П. Никитин // Вестник Пермского гос. техн. ун-та. Сер. «Машиностроение, материаловедение». – 2010. – № 12. – С. 31–47.
- Eskandari, S. Positional, geometrical, and thermal errors compensation by tool path modification using three methods of regression, neural networks, and fuzzy logic / S. Eskandari, B. Arezoo, A. Abdullah // The International Journal of Advanced Manufacturing Technology. – 2013. – Vol. 659. – P. 1635–1649. DOI: 10.1007/s00170-012-4285-y
- Effect of tool setting error on the topography of surfaces machined by peripheral milling / M. Arizmendi, J. Fernandez, A. Gil, F. Veiga // International Journal of Machine Tools and Manufacture. – 2009. – Vol. 49(1). – P. 36–52. DOI: 10.1016/j.procir.2016.10.080
- Chiu, H.W. Prediction of machining accuracy and surface quality for CNC machine tools using data driven approach / H.W. Chiu, C.H. Lee // Advances in Engineering Software. – 2017. – Vol. 114. – P. 246–257. DOI: 10.1016/j.advengsoft.2017.07.008
- Maher, I. Cutting force-based adaptive neuro-fuzzy approach for accurate surface roughness prediction in end milling operation for intelligent machining / I. Maher, M. Eltaib, A. Sarhan, R.M. El-Zahry // The International Journal of Advanced Manufacturing Technology. – 2014. – Vol. 76. – P. 1459–1467. DOI 10.1007/s00170-014-6379-1
- Soori, M. Accuracy analysis of tool deflection error modelling in prediction of milled surfaces by a virtual machining system / M. Soori, B. Arezoo, M. Habib // International Journal of Computer Applications in Technology. – 2017. – Vol. 55(4). – P. 308–321. DOI: 10.1504/IJCAT.2017.10006843
- Vahebi, M. Accuracy improvement of volumetric error modeling in CNC machine tools / M. Vahebi, Arezoo // Int. J. Adv Manuf Technol. – 2018. – Vol. 95. – P. 2243–2257. – http://doi.org/10.1007/s00170-017-1294-x
- Time-Domain Surface Grinding Model for Dynamic Simulation / M. Leonesio, P. Parenti, A. Cassinari et al. // Procedia CIRP. – 2012. – Vol. 4. – P. 166–171. DOI: 10.1016/j.procir.2012.10.030
- Amon, G. Modeling of Vibration Condition in Flat Surface Grinding Process / G. Amon, W. Jin, A. Uwimbabazi // Shock and Vibration. – 2020. – Vol. 12. – P. 1–12. – http://doi.org/10.1155/2020/3069895
- Шипулин, Л.В. Имитационная модель прогнозирования рельефа поверхности в процессе ее формирования при круглом врезном шлифовании / Л.В. Шипулин // Наука ЮУрГУ: материалы 68-й научной конференции. – 2016. – С. 270–277.
- Gong, Y.D. The simulation of grinding wheels and ground surface roughness based on virtual reality technology / Y.D. Gong, B. Wang, W.S. Wang // Journal of Materials Processing Technology. – 2002. – Vol. 129. – P. 123–126. DOI: 10.1016/S0924-0136(02)00589-7
- Hecker, R.L. Predictive modeling of surface roughness in grinding / R.L. Hecker, S.Y. Liang // International Journal of Machine Tools & Manufacture. – 2003. – Vol. 43. – P. 755–759. DOI: 10.1080/10910344.2015.1018535
- Zhou, X. Modeling and predicting surface roughness of the grinding process / X. Zhou, F. Xi // International Journal of Machine Tools & Manufacture. – 2002. – Vol. 42. – P. 969–977. DOI: 10.1016/S0890-6955(02)00011-1
- Yudin, S. Generalized cutting force model for grinding / S. Yudin, K. Smolyanoy, P. Pereverzev // IOP Conference Series Materials Science and Engineering. – 2020. – Vol. 709, no. 033005. DOI: 10.1088/1757-899X/709/3/033005
- Designing optimal automatic cycles of round grinding based on the synthesis of digital twin technologies and dynamic programming method / P.P. Pereverzev, A.V. Akintseva, M.K. Alsigar, D.V. Ardashev // Inter. J. Mechanical Sciences. – 2019. – Vol. 1. – P. 1–11. DOI: 10.5194/ms-10-331-2019


