Модель распределения ассимилятов и оптимального роста растительного покрова

Моделирование динамики роста биомассы органов растений совместно с переносом тепла и влаги в системе «почва – растительный покров» – одна из базовых задач описания функционирования агроценозов и их урожайности, [1; 5; 7]. Особый интерес представляют исследования механизмов адаптации растительных сообществ с помощью вариационных методов. В статье на основе модели роста биомасс растительного покрова в условиях дефицита влаги исследуется распределение ассимилятов фотосинтеза по органам растения, максимизирующее биомассу репродуктивных органов. Полученная стратегия распределения ассимилятов приводит к магистральному сбалансированному характеру роста биомасс, структурирующему и упрощающему модель.

1. Модель переноса влаги и тепла в растительном покрове

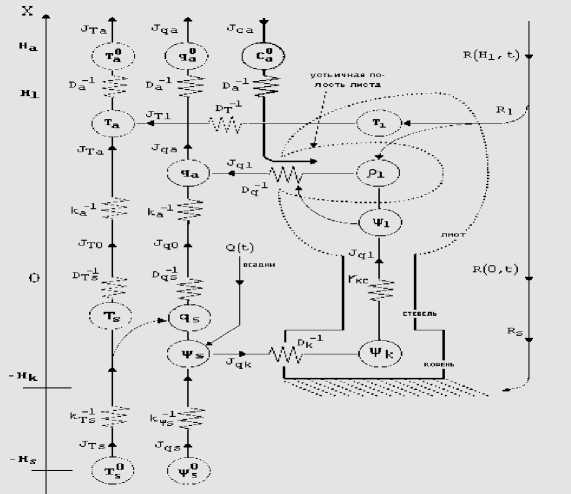
Рис. 1. Схема переноса тепла, влаги и CO ₂ в РП

Приведем систему уравнений модели переноса, описанной в [1-5]. В слое 0 < x < Hl растительного покрова (РП) и в корнеобитаемом слое - Hs < x < 0 почвы рассматриваются две подсистемы уравнений (1)-(4) для температуры воздуха Ta , листьев Tl , концентрации водяного пара в межлистном воздухе qa , в устьичных полостях листьев ql :

JTa = - Cpka 3 Ta lxx >           Jqa =- ka 3Ча I3x •      0 < x < Hl i

Cp STa/8t = -8JTa (8.x + /„ , 8Ча /51 = - 8J_/8x + f„ ,(2)

/„ = CpDTSl Tl- Ta )Pl , fql = DqSl (4i — Ча )Pl ,(3)

/ti + Xfqi =8R1I/8x ;(4)

и две подсистемы (5-7) для температуры T_s и водного потенциала v s <  0 почвы:

JTs =-cpkTsdTs/sx,         J*, = -kVs a^s/5x,    -Hs < x < 0(5)

Cs dTs/St = -dJTs /dx, S 9Vs/St = -dJvs /5x - V ,

V = JqiPk+ DkSk (Vs- Vs) Pk;

а также подсистема для концентрации углекислого газа CO ₂

Jca =-ka 9Ca /5x ,(8)

5Ca (бt = -dJca dx + fd ,(9)

fl = DcSl (Cl - Ca )Pl ,(10)

с краевыми условиями:

JTa = CpDa (Ta - T," ) ,           Jqa = Da (qa - Ч^ ),    x = Hl ,(11)

J Ca = D a ( C l - C a ) i

JTa = CpDTs (Ts - Ta ) ,           Jqa = Dqs (4s - 4a ) ,    x = 0 ,(12)

J c, = 0 ;

JTa + XJqa - JTs = R (0 ,t) ,       - Jvs + Jqa = Q (t), x = 0,(13)

Ts = Ts0,                        Vs = Vs,              x = -Hs.(14)

Транспорт воды в растениях и испарение ими влаги Jql (транспирация) регулируется вод- ным потенциалом листьев vl, их устьичным сопротивлением rst и описывается нелинейными выражениями:

н ¹                                    _

J ql = J fqldx , J ql = ^D k ^V V_S - V l ) , при V m <  V l <  V s <  ⁰,            ⁽¹⁵⁾

где Vs = JVsPkdx, Mi = Vl/Vm , 1 Dq = Vdt + rst , VDk = rkc +1 (DkSk) , - Hk rst = rs о(1 - §iMi)(1 - Mi)"*, 0 < Mi < 1, §i > 0; Ms = Vs lvm ;            (16)

J ql = ⁰, при V s ^ V m <  ⁰-

Подсистема уравнений, описывающая распределение углеводов, преобразование поглощенного CO ₂ в углеводы, затем в биомассу органов и рост биомассы листьев (i=l), корней (i=r), репродуктивных органов (i=R) и стеблей (i=s), имеет вид [6,7]:

A mi = р z. (t )ф,А t — RT mA t- Ri A mi, или

Ф‘ mii =рi(t)-—~--Rmi, ^рi(t)=1, рi(t)^0, i^{l,r,R,s},

• ¹    + R i

где

Ф; = SiтФ0 , R; = R'(Ti)(1 + Ri), A ^T, Ф0 = rTTA---ZT,(19)

^(a I Ф ) ⁺ r c c l

Г = SlD- + D- , r = A1r + rc .(20)

Здесь J_Ta ( x,t ) , J_qa ( x,t ) , J_ca ( x,t ) - потоки тепла, водяного пара и углекислого газа CO ₂ в межлистном воздухе, J_Ts ( x,t ) , J _{V s} ( x,t ) - потоки тепла и воды в почве; V s ( t ) — усредненный водный потенциал корнеобитаемого слоя почвы, v _l ( t ) - водный потенциал листьев.

Продукты Ф'А t фотосинтеза распределяются по органам растения долями р i ( t ) и используются для роста A m i органов; при этом часть углеводов расходуется на дыхание поддержания R^,_i(T_l ) m i A t и дыхание роста R i A m i . Температурный фактор ^ ( T ) и константы Б ф , a , r_c определяют влияние потока фотосинтетически активной радиации (ФАР) и концентрации c_l на скорость Ф ₀ преобразования CO ₂ в ассимиляты единицей поверхности листа.

Дифференциальные уравнения систем связаны алгебраическими выражениями (4), (10), описывающими балансы энергии в межлистном воздухе и на поверхности почвы.

Введем обозначения:

da (х, t) = р(Ta) - q, ds (t) - p(Ts (0, t)) - qs (t) , da = p(Ta0)- q°(t), p(T)=p(Ti)+5(t - i), k (х) = ka(х) , G =  ----177-^, G = G (1 - b), G, = G (1 - b);

• 1+ 5x / Cp       1 + Cp/М        '     >>

• 1    = H d^    1 -^XL = 1 + 1 = Hi A.   1 = 5x    1 = 1

Dak   1 ka (X) ' D)k   c.D. ' 4   Dak Dak { kft) ' DTa   cpD, ' D)   DD

• 1      5x      1 5x       1  _ 1       1 _ 1     1     1 _  11

,      —         , —           , -        , - + , -      +

• d t s    C p D Ts    D t    C p D t S i   D q    D q S i Di D q   d t  D s D qs d t s

• b i - G "‘ D , b s - G -¹ D , D _z- D a + D . + D S , D _e ^- D ) + D T + D s .

2. Приближенная модель переноса влаги и тепла

Для модели (1)-(11) получим приближенную модель при условиях

D' Id ; <<  1, D' id' <<  1, AD_y Id' <<  1. ^ T             ^ is                ^ Hk

(22)

Здесь запись a <<  1

математически эквивалентна a ^ 0; она используется

из-за своей боль-

шей физической содержательности.

Введем обозначения

в - ( D a + D s )/ d ; , b - D s /( d) + D s ) ;

(23)

d t - ( _z ^{- 1} gr) + D a d a ⁰+ D s d s )/( D a + D s ) ;

(24)

J qa - bJ + a ,

J qa - X - GR a + D a d a ;

(25)

J Ta - bJ - a + ( 1 - Ь ) R a ,

J ia - ( 1 - G ) R a ⁰ - x d) d a ⁰;

(26)

d a ⁺ - d t ,

d a - 0 ;

(27)

q - ^- q a ^{+ J} - a 1 ^D a ,

q a ^{+ -} q a ^{0 + b - 1 (} q a ^- q a ⁰ ) ;

(28)

T_tt- T a" + J- a ^pD) ) ,

.               T a ⁺- T a ⁰ + b ( t, -- T a ⁰ ) + ( 1 - b ) r) /( c p D a ) .

(29)

DT

Отметим, что введенные величины положительны, кроме, возможно, G l и G _s . Очевидно, d ;/ d t < 1, D s/ d t s <  1.

В [5] доказано, что в условиях (22) справедлива система

59w/5t --5Jvs /5X - JqlPk , Jql - Jq+a /(1 + в) , - Hs < X < 0, (30) - Jvs x-0 + Jq 0 - Q(t), Jq 0 - PbJq) /(1 + в); X-0; (31) Vs - Vs; X - - Hs; где

J ,s -- k ,s d^ s/д х , c v -^ < 0, ⁵V s

( D' ^;+ D s ) r o 1 -5 i p        J + a   1           1 + D k ( F kc S k )

P ^-_c          — ⁺ A kc „ . — ; A kc ^-        „    ,

Si      1 -Ps       Sk 1 -Ps          -VmDk при 0 < ps < 1, в - да при 1 < ps .

Проинтегрируем (30) на отрезке [ - H_k, 0 ] с учетом J_q) - J_ql + J_{q 0}:

W + J qa - Q ⁽ t ) - J _v sHk - 0, w - f 9 w dx - H k 9 w , J , sHk - J , s I

• - H k                                         ^{lX -} H k

3. Модель фотосинтеза растительного покрова

Чтобы сделать нижеследующие оценки примем два допущения. Во-первых, примем, что из определения cv -59w /5^s для графика 9w -9w (vs) основной гидрофизической характеристи- ки (ОГХ) с достаточной точностью следует cV =50w /суs для зависимости средней влажности Оw от среднего потенциала Vs по слою [- Hk,0] • Дополнительно примем зависимость Vs = Ae~aw0w • Тогда (34), (33) преобразуется к виду:

d" Йs =аwЙs [Jqa (Йs ) —Q(t) —JvsHk ] , Vs = ЙsVm , aw = aH— ,            (35)

^J qa ⁽Й s ) = J qa 11^ , при 0 <  _{M s} <  1, ^J qa ( ц ' ) = bT ^ , при 1 <Ц ' •           (36)

Получим приближенную модель фотосинтеза растительного покрова, предположив, что в системе уравнений (8)-(10): а) концентрации c_a , c l , фотосинтетически активная радиация I ф незначительно изменяются внутри растительного покрова; б) покров находится в состояние квазистационарного равновесия в отношении cl , т.е. 5 cl/дt ~ 0.

С учетом сделанных предположений проинтегрируем (9)-(10) по высоте покрова на отрезке 0 <  x <  H l :

—

^{[ j} ca l x = H

^{— J} ca |x = 0 ^]+ J 0 ' D c S l ⁽ c l ^— c a ) P l dx = ⁰ •

С учетом (10)-(12) получим — D a ( c a — c 0 ) + DS ( c l — c a ) = 0. Выразив отсюда c_a — c l и подставив в (10), получим выражение для потока CO ₂ , поглощаемого листьями в единице объема РП:

^fcl = ^—

D a D c S l

D a + D c S l

^{( c 0 —} c l ) P l •

Интегрируя это в поглощенного стол CO 2 , поглощенног c l = c 0 — Г 1 Ф 0 в (19),	ыражение на 0 <  x <  Hl , т.е. по высоте РП, получим величину Sl Ф 0 CO 2, бом РП с единичным основанием за единицу времени. Отсюда величина ) единицей поверхности листа, будет равна Ф 0 = ( c 0 — cl )/ r 1 . Подставляя получим для Ф 0 уравнение Г 1 Ф 2 — ( c0 + r а I ф ) ф 0 + A 1 c0 « I ф = 0 , Ф 0 = 2 ( r — r ) [ c a + r “ I Ф ( c 0Ca r “ I Ф ) + 4 r c “ I Ф c a = = A 1 c 0 ___________2 v___________ v = r a I ф                            (37) r 1 + v + V( 1 — v ) 2 + 4 vjr       ca
Легко видеть, Ф нейшем для получе вать следующие бол	0 ~ A 1 c0 / r при v ^ да , например, при I ф ^ да или r ^ да . Однако в даль-ния явных оценок в условиях дефицита почвенной влаги будем использо-ее сильные условия. D — = . r' 1 ( 1 6 1 Й s ) + A kc „’"„ S l . (38) 1 — Ц ' L r ' 0 D a + D ' S r J
В самом деле, (38	) прямо следует из (33), (23), (22): e = ( D a + D ' ) ( 1 D ’ + 1 D T M D a + D ' )/ ( D q S l ) .
Пусть r s<<  D — 1 mes       q	<< r cut , S l D a 1<<  D q 1 . Из (16) следует D q 1 = r 't + D T 1 ~ r 't , D —1 = V ( r ' — 1 + r cut ) + r mes ~ D q' , r 1 = S l D a 1 + D — « D — « D q1 .                           (39)
Таким образом, п	ри выполнении приведенных выше приближенных равенств (39) Ф 0 « c " jrx « c " D q .                                                  (40)
Введем обозначе	ния

^K- m k- , S i ^-p m , S k =P _A , m_l

B 1 - 1 -8 i ц s , B 2 =

^A kc    ^J qa P l

r s о D ‘+ D ’e k

^в l ^T c a     ~   ~

, ^Ф 1 -^1+^ ’ ^R i = ^R ,

G ^(X , ^H s ,t ) = ^TT⁽¹ — ^ s ) , F ( ^X , ^ s ,t ) = G Yr s ^Ф 1

B ^ K + B 2                        K + 1

Уточним (40):

r ~ D - - r s о ( 1 -ц s ) ^{- 1} ( B 1 K + B 2 ! л ,

Ф'      S,TC°                   x h ~ - A ~ Y - mlФ^(K,цs,t).

⁽ 1 ⁺ R i ) ⁽ 1 ⁺ R i r

Для приближения (40) модели фотосинтеза выпишем модель роста четырех биомасс m i ( t ) растительного покрова и сопряженную с ней модель динамики усредненного водного потенциала ц _s корнеобитаемого слоя почвы:

d-m, - рi(t)mlG(K,цs,t)Ф1 -Rmi , i e {l.k.R.s} ;(43)

dt d Цs -a w цs [Jqa (u s )-Q (t )-J„sHk ] , JqQ (цs )-J+ ’ ’ ^^ ;

t+ U

Spi (t)- 1 , Pi (t)-0 , P- (D д Ds -rs 0A , ^s -Цs ^ m , 0 < Ms < 1;

m i p i G ⁽K , ц s i )

m i ^{( 0 )- m 0, ц} s ^{( 0 )-ц 0} .

• 2.    Рациональное распределение ассимилятов

Рост биомасс m i ( t ) в (43) зависит от значений ростовых функций р i ( t ) , моделирующих сложные механизмы распределения и транспорта ассимилятов в растении. Обычно функции р i ( t ) определяются натурными измерениями.

Варьируя р i ( t ) можно в значительной степени регулировать рост всех биомасс m i ( t ) и, следовательно, величину биомассы m_R ( t ) репродуктивного органа в конце жизненного цикла растения [ 0 ,Т ] . Представляет интерес определить такие р i ( t ) , при которых m_R ( t ) достигает максимума. Разумно пр едполагать, что такая структура распределения ассимилятов может возникать эволюционно у некоторых видов растений, например злаковых, подвергаемых отбору на максимальную урожайность репродуктивных органов.

Рассмотрим задачу выбора функций рi (t), максимизирующих для системы (43)-(45) на [0,Т] функционал mR (Т) ^ max                                  (46)

при ограничениях (45). Для частного случая, когда параметры внешней среды постоянны, в частности постоянны водный потенциал ц _s и температура листьев T l , в [6] доказана теорема о магистрали для m i ( t ) из (43). Опишем содержательную интерпретацию результатов формальной теоремы, представленных на рис. 2 и 3, где m 1 - m l , m 2 - m_k , m 3 - m_R . Заметим, что оптимальные р _s ( t ) - 0, ибо из-за отсутствия в модели (43)-(45) учета архитектоники растения затраты ассимилятов на рост биомассы m_s стеблей оказываются непродуктивными. Также нетрудно видеть, что затраты ассимилятов на рост m_R продуктивны лишь на заключительном репродуктивном периоде [ т ₂ ,Т ] . Для начального вегетационного периода T 1 <  t <т ₂ рассмотрим функцию F ( K , ц _s,t ) удельной фотосинтетической мощности покрова, приходящейся на единицу суммарной биомассы

F ( K , ц s t ) --^^ G ( K , ц s ,t ) Ф 1                            (47)

m l + m k

Функция F имеет единственный максимум при X * = ^B\ /В ₁ - решении уравнения

_L F=Ф (1 _й )d      X          -в^2+в2

dX Л Цs’d (X +1)(B1X + B2) (X +1)2(B1X + B2)2

равный F* = Ф1 (1 - цs )(тв"+вг- )г2 . Оптимальные р* (t) и рк (t), отвечающие F*, есть реше- ния системы ml = рlmlGФ1 - Rml , mk = рkmkGФ1 - Rmk , mk = X*ml, рl + рk = 1 .

Отсюда следует

1                    X *

^X = V ^B 2/ ^в 1 , р / =Г^ , р к =r"v , P R = 0 ’ P s = 0, t ^G [ T ’ ^T 2 ) •       ⁽⁴⁸⁾

1+ X 1+ X

Итак, период роста [ 0 ,T ] разбивается на три фазы: начальную [ 0 , т ₁ ) , вегетативную [ т ₁ , т ₂ ) и репродуктивную [ т ₂ ,Т ] . На начальной фазе система стремится достичь сбалансированного отношения биомасс корней и листьев X * , направляя все ассимиляты на рост органа с недостаточной биомассой. Например, начальное значение X ⁰ > X * на рис. 3 характеризуется недостаточной биомассой листьев m_l , поэтому все ассимиляты направляются на рост листьев, т.е,

р l = 1, р к = 0, р R = 0, р s = 0,                             0 ^ t ^т1

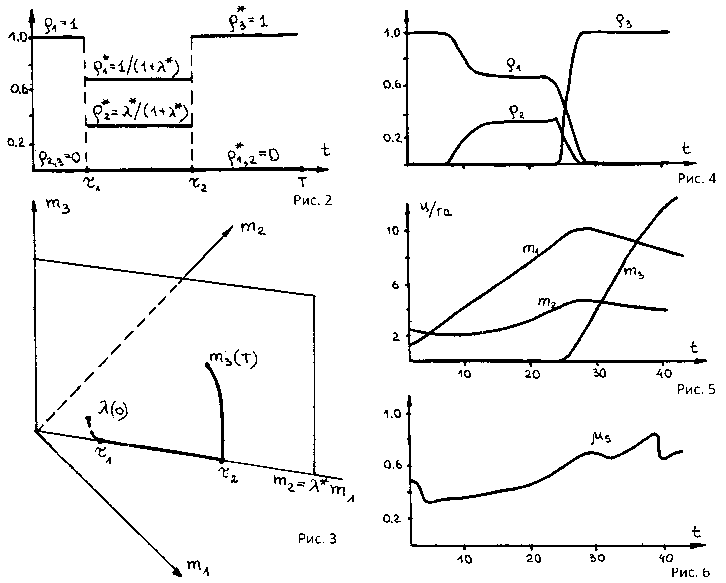
Рис. 2–6. Оптимальное решение модели (43)–(46)

В момент т1 отношение X(t) становится равным X*, система достигает магистрали m2 =X*m1 и переходит в состояние сбалансированного роста. Это - вегетативная фаза, в течение которой выполняется (48). Скорость роста зависит от условий среды, в частности от усред- ненного водного потенциала цs.

С момента т2 начинается третья репродуктивная фаза, при которой все ассимиляты направляются на рост репродуктивной биомассы mR р1 = 0, рк = 0, рR = 1, рs = 0,                             т2 < t < T .

В момент времени T система заканчивает рост с максимальным значением m_R ( Т ) . На рис. 4–6 показаны численные решения задачи (43)–(46).

Таким образом, оптимальное сбалансированное распределение ассимилятов соответствует максимизации удельной мощности фотосинтеза F(X,цs,t). Траектория магистрали обладает эффектом «притяжения» оптимальных траекторий с другими значениями начальных и внешних условий. Можно ожидать, что использование магистрали позволит лучше структурировать модель растительного покрова.