Модель рассеяния микроволн от двухслойной среды с шероховатыми границами

Наряду с амплитудой, основной характеристикой радиоволны является его фаза, пропорциональная пути, пройденному волной. Свойства фазы, точнее, разности фаз, изначально использовались в радионавигации и в последние десятилетия нашли широкое применение в глобальных навигационных спутниковых системах.

Интерферометрические методы нашли широкое применение в космическом радиолокационном дистанционном зондировании Земли. При ин- терпретации данных зондирования интерферометрическим радарами основой информативной характеристикой является интерферометрическая фаза радиолокационного сигнала, рассеянного земной поверхностью. Используемые до последнего времени расчетные методы практически не учитывают зависимость фазы радиолокационного сигнала от физических и геометрических свойств почвенных покровов, в частности от слоистой структуры приповерхностной почвы. Обычно при анализе работы интерферометрических радаров используется следующее выражение для интерферометрической фазы сигнала [1]

Ф = Ф topo + Ф def + Ф atm + Ф noise , ⁽¹⁾ где слагаемое ф_1оро возникает вследствие рельефа, компонента ф^ описывает влияние деформаций земной поверхности за время между пролетами спутника, составляющая ф_а1т возникает вследствие неоднородности атмосферы, слагаемое ф_noise обусловлено шумами приемно-передающего оборудования.

В формуле (1) не учитывается зависимость фазы сигнала от изменения отражательных свойств поверхности, которая может быть обусловлена слоистой структурой влажности почвы, влиянием замерзания верхнего слоя почвы и другими факторами. Между тем, вариации фазы могут существенно уменьшить точность метода дифференциальной интерферометрии, используемой для определения деформаций и подвижек земных покровов и сооружений на них [2]. Ранее, в работах [3-5] было показано, что слоистость земных покровов вызывает заметные вариации фазы отраженного сигнала. В данной работе исследуется влияние двухслойной среды с шероховатыми границами раздела на фазу микроволн при обратном рассеянии в рамках предложенной приближенной модели.

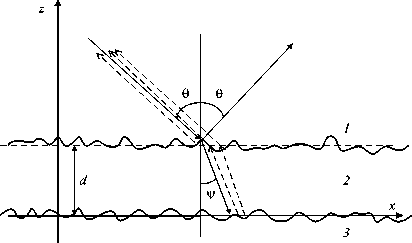
Рис. 1. Геометрия задачи об обратном рассеянии

2.    Фаза волны при обратном рассеянии

Найдем поле обратного рассеяния. Как показано на рис. 3, это поле является суммой волн, испытавших различное число отражений и преломлений. Во-первых, это волна, рассеянная верхней граничной поверхностью 12 между средами 1 и 2; затем волна, прошедшая (преломившаяся) в слой через границу 12, рассеянная от нижней границы 23 и затем прошедшая границу 21 и т. д. Поскольку неровности малы, будем полагать, что коэффициенты прохождения определяются формулами Френеля (борновское приближение). Введем понятие коэффициента обратного отражения по полю от шероховатой поверхности, равного отношению напряженности рассеянного поля, к напряженности падающего поля. Тогда коэффициент обратного отражения от слоя с шероховатыми границами можно представить в виде r = Г12 + 712Г23T21 e2k2dco' Х^ '23e2"2d'"')'                 (2)

n = 0

где r 12 и r 23 – коэффициенты обратного отражения по полю от верхней и нижней поверхностей, соответственно; Т 12 и Т 21 – коэффициенты прохождения через верхнюю границу, k 2 – волновое число в слое, θ 2 – угол преломления, определяемый законом Снеллиуса.

Используя формулу для бесконечной геометрической прогрессии, по- лучим r 2 + 1 _ P2 V z,2 ik 2 d/cos '

r = ' 12 ^{+ (} ' 12 ^{+ l 2} 42 ) ' 23 e (3)

1 .              2 ik-,d /cos '              ,

^{1 +} r 12 r 23 e ²

где R 12 - коэффициент отражения Френеля от второй среды.

Учитывая, что r12, r23 << 1 и полагая, что неровности верхней и нижней поверхностей не коррелированы между собой, после усреднения получим

(г ) = ( r ,2} + (( r , ² 2) + 1 - R 12 ) ' 23) e ^!"^{2 d} /"* '             (4)

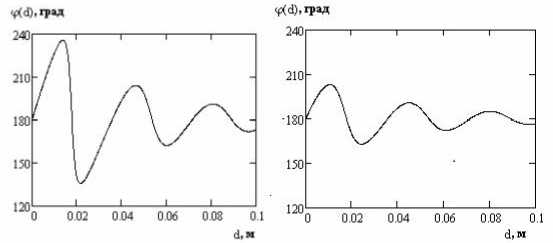
Поскольку мы ограничиваемся малыми неровностями, для оценок (4) можно использовать результаты метода малых возмущений [6]. Коэффициент rr^ связан с коэффициентом обратного рассеяния ст 0, который обычно определяется во всех теориях радарного рассеяния, соотношением Гг^ = д/70/4п . На рис. 2 приведены построенные по формуле (4) зависимости фазы коэффициента r от толщины слоя на длине волны 23,5 см при следующих параметрах: длина волны λ = 23 см, угол ψ = 30°, ε2 = 8 + 4i; на рис. 2а средние коэффициенты обратного отражения r12 = 0,02, r23 = 0,03, а на рис. 2б – r12 = 0,03, r23 = 0,02, R12 = 0,5.

• а)                                  б)

Рис. 2. Зависимости фазы среднего коэффициента обратного отражения от толщины слоя

Наибольшее влияние слоистости почвы на изменения амплитуды и фазы отраженного сигнала проявляется в том случае, когда на влажной почве находится сравнительно сухой слой. Изменения фазы в зависимости от толщины слоя могут достигать нескольких десятков градусов. Эти вариации фазы могут являться источником заметных ошибок при использовании метода дифференциальной интерферометрии и, следовательно, их необходимо учитывать при его практическом применении.

Заключение

В работе представлены возможные вариации фазы микроволн при отражении и рассеянии от двухслойной влажной почвы. Установлено, что слоистость почвы может приводить к заметным изменениям фазы. Полученные результаты для двухслойной почвы могут служить основой для анализа многослойной среды и непрерывной слоистости. Сделан вывод о необходимости учета вариаций фазы для метода дифференциальной интерферометрии.