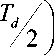Model Reference PID Control of an Electro-hydraulic Drive
Автор: Ayman A. Aly
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 11 vol.4, 2012 года.
Бесплатный доступ
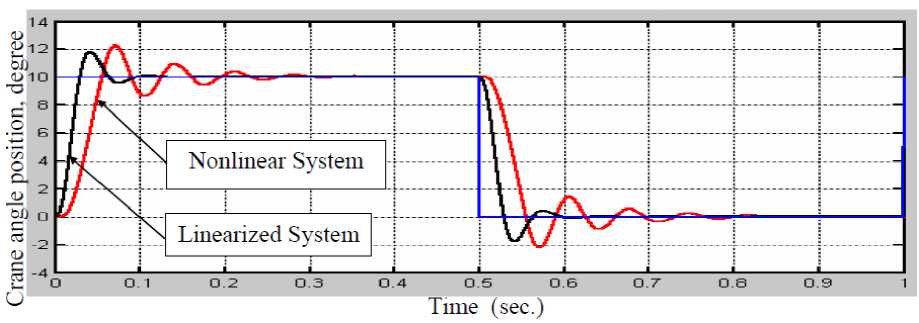
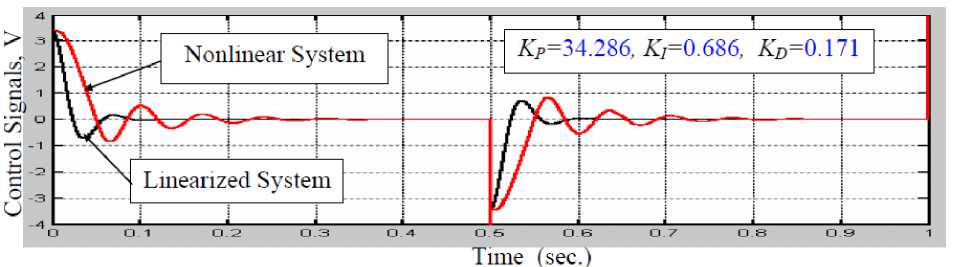
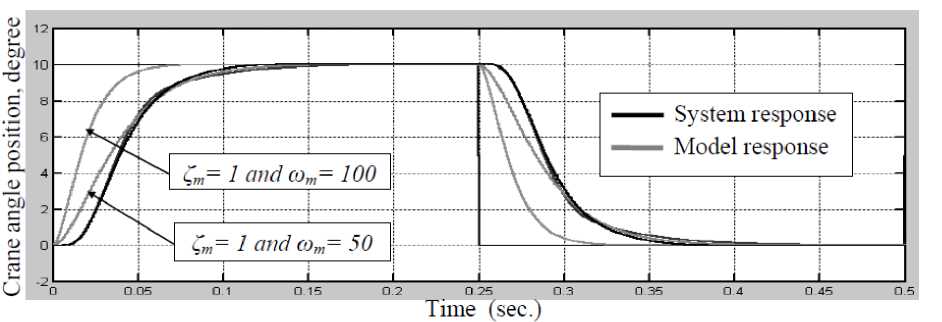
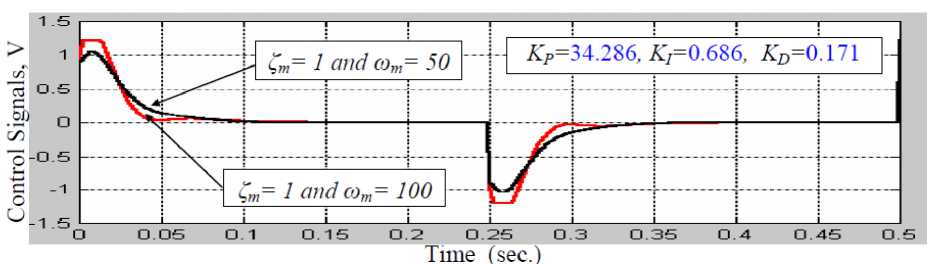
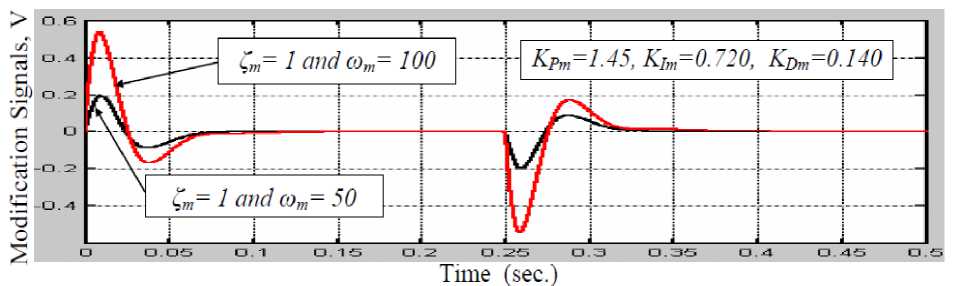
Hydraulic cranes are inherently nonlinear and contain components exhibiting strong friction, saturation, variable inertia mechanical loads, etc. The characteristics of these non-linear components are usually not known exactly as structure or parameters. For these reasons, tuning of the traditional PID controller parameters to control this system for the required performance faces a strong challenge. In this paper a new approach to design an adaptive PID control has the ability to solve the control problem of highly nonlinear systems such as the hydraulic crane was proposed. The core of the design method depends on comparing the performance of the Model Reference (MR) response with the nonlinear model response and feeding an adaptation signal to the PID control system to eliminate the error in between. It is found that the proposed MR-PID control policy provided the most consistent performance in terms of rise time and settling time regardless of the nonlinearities.
Hydraulic Crane, Nonlinear PID, Model Reference, Adaptive Control
Короткий адрес: https://sciup.org/15010328
IDR: 15010328
Текст научной статьи Model Reference PID Control of an Electro-hydraulic Drive
Published Online October 2012 in MECS
Electrohydraulic drives are widely used in industrial applications, such as in rolling and paper mills, as ‘‘actuators’’ in aircraft, and in many different automation and mechanization systems. The main reason for their broad industrial applications is the great power capacity that they can exert (as compared to their DC or AC counterparts), while preserving good dynamic response and system resolution, [1].
Hydraulic systems consist of various elements: pumps, actuators, control valves, accumulators, restrictors, pipelines and the like, which include many types of nonlinearities, such as pressure-flow characteristics in control valves, dry friction acting on actuators and moving parts of valves, collision of valves against valve seats, [2]. It is a marked feature of nonlinear systems that global behaviors are sometimes quite different from local behaviors. In such cases, results of linear analysis are unavailable to estimate global nature of the system.
Systems containing fluid power components offer interesting and challenging applications of modern and classical control techniques. The use of microcomputers and many feedback devices for hydraulic drives allows for implementation of different control algorithms that result in better steady-state and dynamic performances in fluid power control systems. There are a number of research results on the applications of adaptive control [2], robust control [3], and variable structure control [4] in electrohydraulic control systems.
In the Sliding Mode Control (SMC) method, the system trajectory is forced to reach the sliding surface and to slide along it, or to remain in its vicinity, [4]. Since in many situations the SMC is found robust to a great extent to plant parameter variations or uncertainties in the model of the system to be controlled, it has found broad applications. However, the chattering is a signify problem in the SMC implementations and solutions that either reduce or eliminate it had been investigated in [5, 6].
In a parallel way, even though fuzzy logic controllers often produce results superior to those of traditional controllers [7], the control engineer has found difficulties in accessing the fuzzy logic controllers because of the following limitations: The design of the fuzzy logic controller is not straight forward due to heuristics involved with control rules and member-ship functions. There is no standard systematic method for tuning the fuzzy logic controller parameters.
Gholamreza and Donath [8] recognized that a hydraulically actuated system contains a host of nonlinear elements, thereby making a linear controller ineffective. Furthermore, the authors illustrated that linearization of the dynamic equations over a small operating range and the design of an appropriate controller for each condition had limitations in the face of time variable parameters changes.
Most of the recent work performed on hydraulically actuated linkages has focused on developing some type of adaptive controller, [2, 3]. These controllers are meant to compensate in real-time for nonlinear elements such as friction and smooth time-variant load changes. These methods rely on continuous noise-free feedback and are generally computationally intense making them non-ideal for application to low cost mobile equipment.
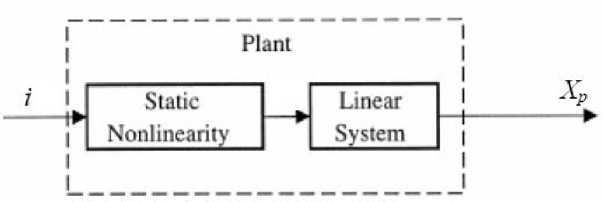
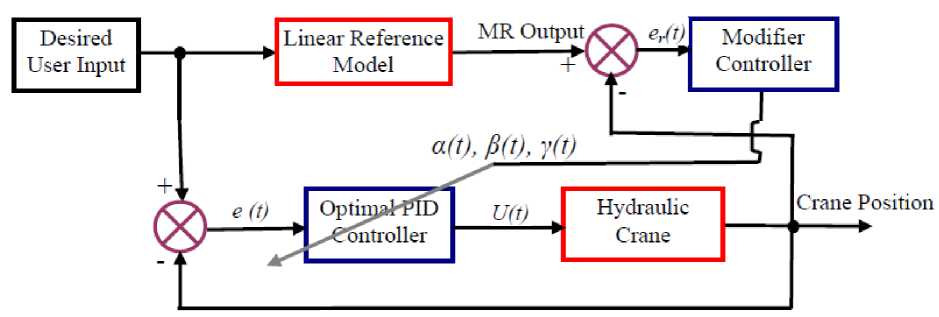
The aim of this paper is to design a nonlinear PID control has the ability to solve the control problem of highly nonlinear systems such as the hydraulic crane, which is shown in Fig.1. This will be done by first deriving a nonlinear mathematical model of the system and then approximating the transfer functions in the model by low order linear transfer functions. Using the low order linear transfer functions, design optimal gains of the PID regulator is determined. The final step is implementing the designed PID controller in the nonlinear model and then comparing the performance of MR response with the nonlinear model and feeding a correction signal to tune the PID control system parameters to eliminate the error in between.
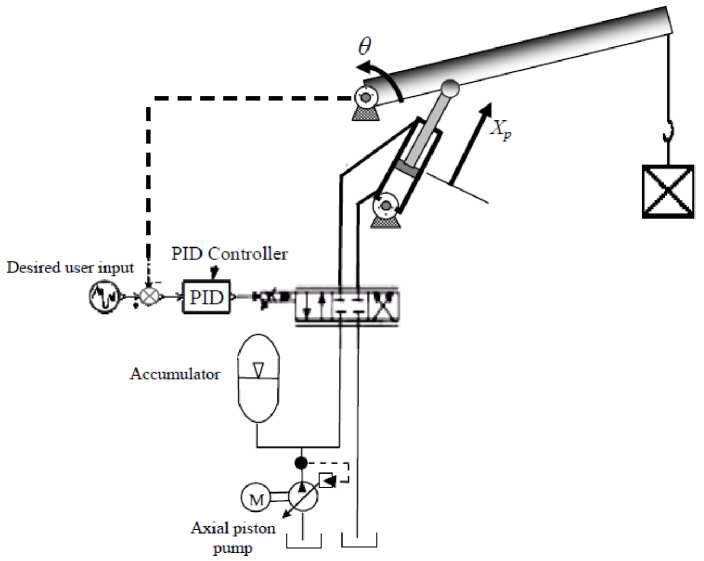
Fig. 1: Hydraulic Crane System
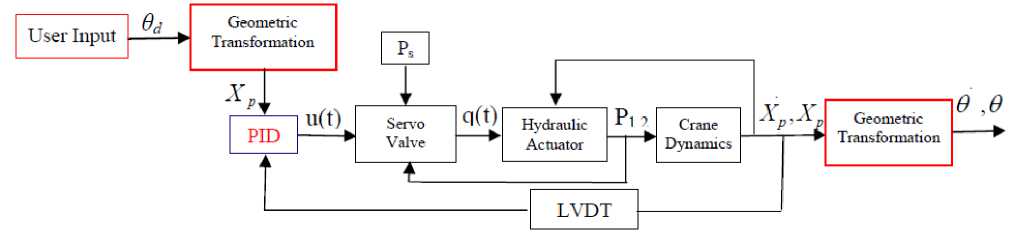
II System Construction
The servo system is composed of a hydraulic power supply, an electrohydraulic servo valve, a cylinder, mechanical linkages, and control. The piston position of the cylinder is controlled as follows: Once the voltage input corresponding to the desired position is transmitted to the servo controller, the controller signal current is generated. Then, the valve spool position is changed according to the input current applied to the torque motor of the servo valve. Depending on the spool position and the load conditions of the piston, the rate as well as the direction of the oils supplied to each cylinder chamber is determined. The motion of the piston then is controlled by these oils.
If it is necessary to represent servo valve dynamics through a wider frequency range, a second-order transfer function must be used. The relation between the servo valve spool position x v and the input current i v can be written as, [2]
d 2 xv dt 2
dx 2
+ 2^v^v —77 + ^v xv dt
= ®v k v i v
where kv represents the gain of the servo valve, ωv is the natural frequency of the servo valve, and ζ v is the damping ratio of the servo valve.
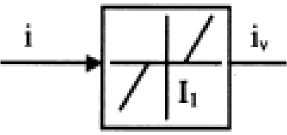
Fig. 2: Characteristic of the dead zone
The valve spool occludes the orifice with some overlap so that for a range of spool positions there is no fluid flow. This overlap prevents leakage losses that increase with wear and tear. Thus, the dead zone should be placed between the valve dynamics and actuator/load dynamics. For the sake of simplicity, this dead zone is equivalently moved to the position between the output of the controller and the input current of the valve. So, the dead zone nonlinearity may be characterized as shown in Fig. 2 and approximately described as:
iv
i -11 ifi > 11
<0 iflil < 11
i + Ix if i < - I,
where i v is the current from the controller and I 1 the width of the dead zone.
The equations of the servo valve flow to and from the actuator (assuming symmetric valve port, zero lap design and zero return pressure) are as follows,
For positive x v
q, = CdWX, sgn( Ps - Pf )I2 P - Pf\
, qn = CdWxv sgn( Pn KpPI ' p (3)
For negative xv
q, = CdWxv sgn(P,)J|P|
,
qn = CdWxv sgn(Ps - P )l2 Ps - Pn|
V p (4)
where x v is the spool displacement, P s is the supply pressure, p is the mass density of the oil, Cd is the discharge coefficient of the orifice, W is the width of the orifice, suffix n denotes the annular side and suffix f denotes the full side.
The linearized flow equation of the actuator is given by [8]:
The motion equation of the crane is given by
PleAe = MeXP + Bg Xp + Fd
where M e represents the equivalent mass of both the variable inertia load and the piston, B e is the equivalent viscous damping coefficient, and Fd represents the disturbing forces like friction forces.
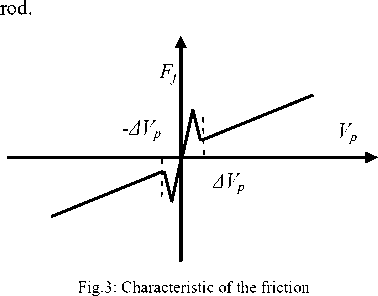
The various friction characteristics depend on lubrication, relative velocities of bodies at the contact point, pressures and others [1, 2]. A typical friction characteristic is presented in Fig.3. The mathematical description of friction process in hydraulic cylinders involves serious difficulties caused by:
-
• Presence of a wide range of different sealing elements in dynamic connections (O-rings, V-type seals, packing seal).
-
• Applications of various sealing materials rubbers or composite materials.
-
• Influence of temperature on friction resistance due to the fact that sealing materials have higher thermal expansion coefficient than metal elements.
• Deposition of solid contaminations on the piston
Ae q = KA
1 +f A T
I A , J
1 +f A *- ‘
I A f J
.
P ie + A e X P +
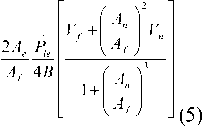
Thus exact simulation of the nonlinear behavior of friction in the vicinity of a zero velocity is difficult. The friction force is approximately simulated by the stick-slip friction law. The value of the stick-slip friction for positive values of Xp is given simply by where
Ple
p$A$ - P n A n n _q , + q n , _A , + A n
A ’ q e = 2 , Ae = 2
Список литературы Model Reference PID Control of an Electro-hydraulic Drive
- H.E. Merrit, “Hydraulic control systems”, John Wiley & Sons, 1976.
- J. Watton. “Fluid power systems: Modeling, simulation, analog and microcomputer control”, Prentice-Hall International, London, UK, 1989
- J.W. Dobchuk, “Control of a Hydraulically Actuated Mechanism Using a Proportional Valve and a Linearizing Feedforward Controller”, PhD, Department of Mechanical Engineering, University of Saskatchewan, Saskatoon, Canada, Aug. 2004.
- A. Bonchis!, P. I. Corke, D. C. Rye and Q. P. Ha, “Variable Structure Methods In Hydraulic Servo Systems Control”, Automatica (37), pp 589-595, 2001.
- Daohang Sha a, Vladimir B. Bajic b and Huayong Yang, “New Model and Sliding Mode Control of hydraulic Elevator Velocity Tracking System”, Simulation Practice and Theory Journal (9), pp 365–385, 2002.
- G. Bartolini, A. Ferrara and E. Usai, “Chattering Avoidance By Second-Order Sliding Mode Control”, IEEE Trans. Autom. Control 43 (2), pp 241–246, 1998.
- Ayman A. Aly and A. Abo-Ismail, “Intelligent Control of A Level Process By Employing Variable Strcure Theory”, Proceeding of International Conference in The Mechanical Production Engineering, Warso, Poland, 1998.
- Ayman A. Aly, Aly S. Abo El-Lail, Kamel A. Shoush and Farhan A. Salem “Intelligent PI Fuzzy Control of An Electro-Hydraulic Manipulator” I.J. Intelligent Systems and Applications, 7, 43-49, 2012.
- Sepehri, N., Lawrence, P.D., Sassani, F., and Frenette, R., “Resolved-Mode Teleportation Control of Heavy-Duty Hydraulic Machines”, ASME Journal of Dynamics Systems, Measurement and Control, V116, N2, pp 232-240, 1994.
- Ayman A. Aly, and H. Ohuchi “Fuzzy Hybrid Control Using Indirect Inference Control For Positioning An Electro-Hydraulic Cylinder”, Conference of Fluid Power System, Yamaguchi, JAPAN, 2001.
- Wilson J. Rugh, “Analytical Framework for Gain scheduling”, American Control Conference, San Diego, California, USA, May 1990.
- Ziegler, J. G., & Nichols, N. B., “Optimum Settings for Automatic Controllers”, Transactions of ASME, 64, pp 759-768, 1942.