Модель роста численности населения Земли в XXI веке

Введение1

Данная статья рассматривает модель насыщенного роста народонаселения Земли в XXI веке, опираясь на известный гиперболический закон, хорошо описывающий рост численности народонаселения Земли на протяжении последних двух тысячелетий [1; 2].

В настоящей работе мы опираемся на подход Сергея Петровича Капицы к глобальным проблемам роста народонаселения Земли. Автору данной статьи довелось обсуждать с Сергеем Петровичем эти вопросы в далёком 1990 году, когда быстрое сокращение населения России было более актуальной проблемой, чем глобальный рост народонаселения. Однако сегодня мы видим, что низкая плотность населения на территории России становится приманкой

ВЕСТНИК 2015

для ряда стран, что создаёт серьёзные риски нашему будущему мирному развитию. Поэтому необходимо задуматься как над проблемами национальной, так и глобальной демографии, чтобы быть готовыми достойно ответить на эти риски.

Сергей Петрович говорил, что «в числе людей на Земле выражен результат всей социальной, экономической и культурной деятельности, что открывает возможность для количественного анализа истории человечества. При анализе этой проблемы всё человечество рассматривается как один объект, как одна развивающаяся система. Сама же модель роста основана на методах и образах физики и обращается к математике для описания явлений прошлого» [3].

Он противопоставлял цельный, феноменологический подход к этой проблеме методу суммирования частных законов развития, свойственных отдельным странам: «Следует подчеркнуть, что феноменологический подход понимается нами так, как это принято в физике, а не в философии. Иными словами, мы обращаемся к общим принципам самоподобного развития, причинности, выраженной в статистических представлениях, и на этой основе строим теоретические модели. Поэтому мы и не обращаемся к так называемым элементарным явлениям, частично описывающим свойства составляющих систему компонент, суммируя которые можно представить целое. Опыт показывает, что даже для более простых, чем человечество, систем такой путь построения модели часто практически неосуществим».

И далее: «Первый и наиболее успешный опыт феноменологического подхода был развит в термодинамике, когда газ рассматривался как система из многих взаимодействующих частиц. Благодаря столкновениям молекул, находящихся в термодинамическом равновесии, их состояние менялось медленно и обратимо. В этом случае можно ввести такие понятия, определяющие термодинамическое состояние системы, как температура и давление, а также обратиться к представлению об энергии и энтропии, не входя в детальное понимание свойств атомов или молекул, составляющих газ» [3].

В основу рассматриваемой здесь модели положен эмпирический закон роста народонаселения Земли, имевший силу на протяжении огромного исторического периода от начала новой эры до третьей четверти прошлого века. Этот закон получил название гиперболического [1; 2]. Он утверждает, что численность народонаселения Земли N на указанном отрезке времени обратно пропорциональна времени, остающемуся до достижения некоторой критической точки, tc.

По разным оценкам учёных, эта критическая точка приходится на 2026 [1] или 2030 [3] годы. В работе австрийского учёного фон Форстера, опубликованной в журнале Science в 1960 году, утверждалось, что в 2026 году население Земли достигнет бесконечности, если сохранится механизм его роста, свойственный двум последним тысячелетиям [1].

Согласно гиперболическому закону, величина, обратная численности населения N, линейно зависит от времени t. На рис. 1 показана зависимость величины 109 / N от времени для интервала от 1800 до 2000 года.

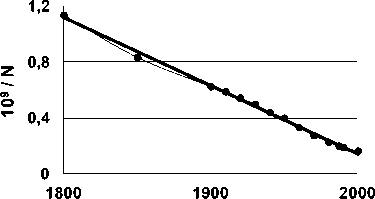
Годы

Рис. 1. Зависимость от времени величины, обратной к численности населения Земли (маркеры), и её аппроксимация прямой линией, стремящейся пересечь ось абсцисс в районе 2030 года

Пересечение оси абсцисс прямой, продолжающей линейный тренд 1/N, означало бы обращение числа людей на Земле в бесконечность. Достижение бесконечной численности населения Земли невозможно по ряду причин [3], поэтому неизбежно насыщение роста. В 80-х годах прошлого века наметилось отклонение от гиперболического закона в сторону замедления темпов роста численности народонаселения Земли. Это замедление к настоящему времени стало весьма заметным, рис. 2. Согласно многочисленным прогнозам, численность народонаселения Земли после 2050 года стабилизируется или даже начнёт снижаться.

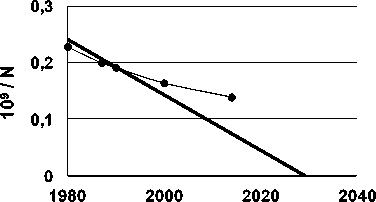
Годы

Рис. 2. Прямолинейное продолжение тренда зависимости 109 / N от времени до 2030 года и отклонения от этой прямой после 1980 года (маркеры)

Цель настоящей статьи – внести коррекции в закон гиперболического роста и рассмотреть модель самоподобного развития численности народонаселения Земли, которая могла бы сделать предсказываемый ею рост сопоставимым с известными прогнозами.

Трудоёмкость удвоения экологической ниши

Гиперболический закон роста численности людей на Земле записывают [3] в виде:

N = L / (tc – t). (1)

Коэффициент L равен произведению N × (tc – – t), и на отрезке времени от начала нашей эры до 1980 г. он близок к постоянной величине в 205 млрд человеко-лет. Как видно, коэффициент L имеет размерность трудоёмкости, что говорит о суммарном вкладе всего человечества в расширение экологической ниши, доступной человечеству на каждом этапе развития технологий жизнеобеспечения [4].

Смысл коэффициента L – трудоёмкость удвоения экологической ниши, растущей с ростом суммы технологий жизнеобеспечения. Так, освоение производства орудий труда, переход от собирательства плодов дикорастущих растений к растениеводству, от охоты – к животноводству,… существенно повысили жизненный потенциал человечества и тем самым способствовали расширению его экологической ниши. Эти достижения были результатом коллективных усилий человечества и быстро распространились на всё человеческое сообщество благодаря способности людей к обучению. Это создавало предпосылки и условия для многократного увеличения численности народонаселения жителей Земли N, пока не возникла проблема ограниченности доступных человечеству природных ресурсов. Постоянство действия гиперболического закона на протяжении многих столетий говорит о постоянстве константы трудоёмкости удвоения экологической ниши в предшествующие века.

В дифференциальной форме гиперболический закон имеет вид:

dN / dt = N2 / L. (2)

Уравнение (2) показывает, что скорость роста числа людей на Земле определяется их взаимодействием, а именно распространением знаний о прогрессивных технологиях жизнеобеспечения.

Можно считать, что трудоёмкость удвоения экологической ниши для крупных животных и предшественников человека, не способных к передаче знаний, много больше современной константы L, что объясняет относительное постоянство их численности. Освоение производства и использования орудий труда и предметов жизнеобеспечения предками человека миллионы лет назад привело к сокращению константы трудоёмкости L до значений, сравнимых с её современной величиной L0.

Нет сомнений, что гиперболический закон, действовавший на протяжении тысячелетий, должен измениться на протяжении нескольких десятилетий. Крутая ломка давно установившихся традиций повлечёт за собой многочисленные перемены в образе жизни человека и общества [3; 4]. Наблюдаемые сегодня отклонения от гиперболического закона, показанные на рис. 2, можно объяснить ростом трудоёмкости удвоения экологической ниши L, вызванным ресурсными ограничениями.

Модель насыщения роста народонаселения

Предлагаемая здесь модель предполагает, что с ростом численности народонаселения трудоёмкость удвоения экологической ниши растёт по степенному закону:

L = L0 + kn Nn. (3)

Здесь L0 – константа удвоения экологической ниши, имевшая место до 1980 года, n – показатель степени для рассматриваемого сценария роста, kn – коэффициент роста для выбранного сценария, определяемый из условия равенства численности народонаселения в 2014 году её современному значению в 7,2 млрд человек. В предлагаемой модели рассмотрены сценарии роста народонаселения, соответствующие показателю степени n от 3 до 7. Мы здесь исходим из концепции самоподобного развития, высказанной С.П. Капицей [3], и связываем механизм торможения роста с численностью народонаселения Земли. Выражение (3) даёт пренебрежимо малое отклонение величины L от L0 при N < 4 млрд человек, что соответствует времени до 80-х годов прошлого века. Зато после 1980 года степенной рост L даёт большие отклонения от L0 всего за 2-3 десятилетия.

Интегрирование системы уравнений (2), (3) даёт прогнозируемый рост численности народонаселения Земли для различных сценариев, рис. 3.

Сценарий роста, соответствующий показателю степени n, равному 7, в наибольшей степени приближается к известным прогнозам достижения к 2050 году численности населения в 10 млрд человек. Меньшие величины этого показателя дают неоправданно большой рост населения.

ВЕСТНИК 2015

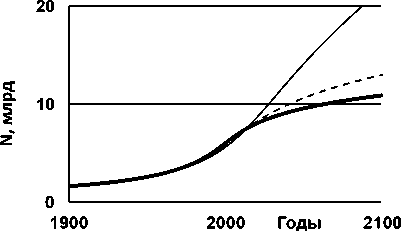
Рис. 3. Предсказание роста численности населения Земли на основе моделей (2), (3) для показателей степени n, равных 3 (тонкая линия), 5 (штриховая линия), 7 (жирная линия)

Уравнение (3) позволяет оценить рост трудоёмкости удвоения экологической ниши для каждого из сценариев, рис. 4.

ВЕСТНИК 2015

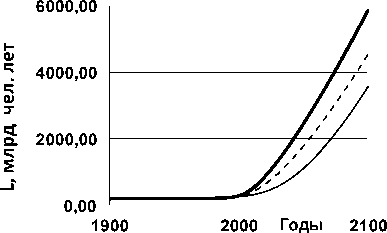
Рис. 4. Прогнозируемый рост трудоёмкости удвоения экологической ниши L для показателей степени n, равных 3 (тонкая линия), 5 (штриховая линия), 7 (жирная линия)

Рисунок показывает, что сценарий с n = 7 требует очень быстрого роста трудоёмкости удвоения экологической ниши. Модель даёт прогноз десятикратного роста этой величины к 2050 году. Такой существенный рост означает коренную ломку традиций, мировоззрения, целей и стремлений людей и общества.