Модель сбалансированного роста межотраслевой экономики региона

Проблемы моделирования межотраслевой региональной экономики в статике и динамике, а также межотраслевых связей с учетом экологических ограничений изучены в достаточной степени. Начиная с работ В. Леонтьева, существенный вклад в развитие данных направлений внесли, например, такие исследователи, как А. Г. Гранберг, К. Миядзава, Р. Миллер, В. А. Колемаев, А. О. Баранов, В. Н. Павлов, Е. В. Рюмина, Г. Р. Серебряков, М. Н. Узяков, А. А. Широв, А. А. Янтовский и др. [2, 8, 9, 11, 12, 14, 15, 16].

Для сценарного анализа эколого-экономических процессов на региональном уровне в Иркутском госуниверситете совместно с другими науч -ными учреждениями СО РАН под руководством В. И. Гурмана разрабатывалась модель взаимодействия природы и экономики региона, экспериментально апробированная на материалах Байкальской природноэкономической системы, а в дальнейшем был разработан и применен универсальный для всех регионов комплекс динамических экологоэкономических моделей «Регион» [10].

В методологическом плане данный комплекс динамических экологоэкономических моделей достаточно глубоко разработан [10, 13]. Однако применение их для описания системного развития экономики региона сталкивается с серьезными трудностями прежде всего информационного характера. В эколого-экономических моделях для описания региональной экономики необходимы дополнительные переменные, связанные с затратами основных фондов, труда, сырья и материалов на охрану природной среды. Кроме того, обратную связь в виде влияния природных ресурсов на развитие региональной экономики приходится пока учитывать вне моделей, в которые, в свою очередь, необходимо вводить границы допустимых норм загрязнений и критерии оптимизации.

В последнее время в Российской Федерации в целом и на уровне некоторых отдельных субъектов после длительного перерыва появились возможности практической разработки статических и динамических межотраслевых моделей в результате составления базовых таблиц «затраты-выпуск», представляющих собой сбалансированные статистические показатели регионального межотраслевого баланса. В частности, в Республике Бурятия такие детализированные таблицы были составлены в 2013 г. на основе Общероссийского классификатора видов экономической деятельности (ОКВЭД). Составленные по 50 видам экономической деятельности данные таблицы с помощью алгоритмов агрегирования были сведены до 10-15 отраслей и до трех агрегированных сфер экономики республики. Разработанные таблицы «затраты-выпуск» Правительством Республики Бурятия были признаны эффективным инструментом прогнозно-аналитических расчетов и были рекомендованы для использования в работе министерств и ведомств. Построенная на основе агрегированных таблиц статическая межотраслевая модель позволила на практике проводить структурный анализ и сценарные расчеты развития республиканской экономики [1, 5].

Между тем актуальными для системного моделирования экономики региона остаются проблемы отражения эколого-экономических процессов, оценки мультипликативных эффектов структурных изменений в расходах и доходах домашних хозяйств, расширения переменных инвестиционного блока для построения межотраслевых моделей в динамической постановке. Серьезным сдерживающим фактором решения данных проблем является ограниченность информационной базы, отличающейся фрагментарностью и недостаточной системностью. Тем не менее исследования в данных направлениях интенсивно развиваются [1, 3, 4, 6, 7].

В данной работе представлен дискретный вариант динамической межотраслевой модели, разработанной для экономики региона с включением мультипликативных эффектов от межотраслевой взаимосвязи потребительских расходов домашних хозяйств с их доходами и региональными выпусками продуктов и услуг. В качестве информационной базы послужили составленные по Республике Бурятия базовые таблицы «затраты-выпуск» и другие официальные и оценочные статистические показатели.

1 Постановка задачи

Для разработки динамической межотраслевой модели возьмем за основу расширенные балансы производства и использования продуктов и услуг, а также балансы использования основного и оборотного капитала:

x - Ax = у ; fx = F , где x = ( x_t ), у = ( у _t ) — векторы валовых выпусков и конечного спроса в регионе, ( i = 1,..., n ; n — число отраслей или видов экономической деятельности); A = ( a j ), ( i , j = 1,2,..., n ) — матрица коэффициентов прямых производственных затрат, f = ( f j ) m _{х n} — матрица капиталоемкости валовых выпусков, F = ( F ,..., F m ) ‘ — вектор m видов капитала.

В среднесрочной и долгосрочной динамике две основные части конечного спроса ( у ) - производственные инвестиции (вектор U ) и непроизводственное потребление домашних хозяйств (вектор С) с введением переменной времени t позволяют представить динамическую межотраслевую модель следующим образом:

x ( t ) = Ax ( t ) + у ( t ) = Ax ( t ) + C ( t ) + U ( t ),                 (1)

U ( t ) = K N F ( t ) = Kf N x ( t ),                   (2)

где K = ( k_u ) _{n х m} — матрица капитальных затрат, показывающая, сколько выпускаемой продукции i - го вида затрачивается для ввода в действие единицы капитала 1- го вида ( l = 1,..., m ). Упрощенно принимая срок создания новых видов капитала равным одному периоду (году), получаем квадратную матрицу приростной капиталоемкости размерности n : B = ( b j ) n х n = Kf .

Коэффициенты матрицы B показывают затраты продукции i -й отрасли на создание единицы производственной мощности в j -й отрасли. С учетом (1) и (2) имеем для региона открытую динамическую воспроизводственную модель Леонтьева в дискретном времени (при A t = 1):

x ( t ) - Ax ( t ) - B A x ( t ) = C ( t ).                      (3)

Тогда при разных траекториях потребления домашних хозяйств C ( t ) решаем систему (3) и получаем согласованные по векторам капитала и непроизводственного потребления объемы валовых выпусков, динамика которых определяет динамику всех остальных переменных модели. Переходя к пределу при A t ^ 0, получаем непрерывный вариант открытого динамического баланса в виде системы линейных дифференциальных уравнений:

x ( t ) - Ax ( t ) - B dx^ = C ( t ).                   (4)

dt

Для оценки траекторий роста всей воспроизводственной системы региона преобразуем открытую динамическую межотраслевую модель к замкнутому виду. Для этого проведем качественное исследование решения урав -нения (3) для одного из способов задания вектора потребления домашних хозяйств C ( t ). Исходим из предположения, что конечный потребительский спрос пропорционален доходам домашних хозяйств, которые, в свою очередь, формируются в процессе производства продуктов и услуг. Для отражения данных взаимосвязей целесообразно воспользоваться подходом японского исследователя Миядзавы к расширению межотраслевой модели путем разработки многосекторного мультипликатора доходов [16].

Пусть C = ( с 1 ,...,c n ) — вектор потребления продуктов (услуг) всеми домашними хозяйствами, каждый элемент которого равен:

q с-=Е cr,(i=i-» n), r=1

где cir — потребление i -го продукта (услуги) r -й доходной группой домашних хозяйств (i = 1,...,n; r = 1,...,q), или элемент матрицы потребления домашних хозяйств:

^с 1 q

C = cnq у

Увяжем потребление домашних хозяйств с получаемыми доходами по каждой группе, тогда имеем:

cr = drzr , где dr — удельное потребление i -го продукта (услуги) в расчете на 1 денежную единицу дохода домашних хозяйств r -й доходной группы (i = 1,....,n; r = 1,...,q), или элемент матрицы удельного потребления домашних хозяйств:

' d 11 L d 1 q d, d

^ n1 nq у zr — общие доходы каждой r -й доходной группы домохозяйств

(r = 1,...,q), или элемент вектора-столбца доходных групп домашних хо зяйств: z = (z1,..., zq ) .

Определим общие потребительские расходы каждой r -й группы домашних хозяйств в увязке с их получаемыми доходами:

nnn

C r = Z C ir = Z d r Z r = z Z d r , ( r = 1,..., q ).

I = 1              i = 1                        i = 1

Пусть e r =^d r ,( r = 1,..., q ). Тогда c_r = P , z , = (1 - s ) z, ,( r = 1,..., q ).

i = 1

Здесь Pr и sr - удельные нормы потребления и сбережения для каж- дой r -й группы домашних хозяйств. По условию Pr + sr = 1.

По каждой r -й группе домашних хозяйств определяем структуру потребления благ:

a ir

c ir c_r

dz d d ir r ir           ir

P r z r

1 - s_r’

( i = 1,

...

, n ; r = 1

...

q ),

n

Z a = ^{1 ( r} = U-, q ).

i = 1

В таком случае, располагая статистическими данными по структуре потребления благ и значениям норм сбережений по каждой r -й группе домашних хозяйств, можно определять матрицу удельного потребления домашних хозяйств:

D =

« 11

( «

^a :^q If ⁽¹. ^{S 1 )}

«nq Д  0

0 )   f d ₁₁

(1 - s q ) J   I d n 1

d 1 q'

d nq У

Таким образом, в целом вектор потребления благ домашними хозяйствами находится в функциональной зависимости от объемов доходов каж-дой r -й группы домашних хозяйств:

С

( n Х 1)

^f d n

^ d n 1

= Dz .

Для получения замкнутого динамического баланса межотраслевой экономики региона необходимо установить функциональную зависимость потребительских расходов домашних хозяйств от объемов валовых вы -пусков. Прежде всего, отметим, что по каждой r -й группе общие доходы домашних хозяйств являются частью валовой выручки , получаемой от производства и реализации продуктов представляется следующим образом:

и услуг. В матричном виде это

z =

Г Z 1 )

^v 11

к zq)

к v4 1

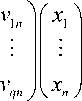
= Vx ,

где V.qхn) = (vrj) — матрица доходов, выплачиваемых r -й группе домашних хозяйств в расчете на единицу стоимости валового выпуска продук ции (услуги) j -й отрасли, т. е. vrj = —, (r = 1,...,q; j = 1,...,n).

x j

Тогда вектор потребительских расходов домашних хозяйств в конечном счете выражается через вектор валовых выпусков: C = DVx = Gx .

В результате произведения двух прямоугольных матриц D ₍ n _{х q} ) и V _{: q х} n ) квадратная матрица G ₍ n _х n ) является вырожденной (ее определитель равен нулю при n >  q ), а каждый из ее элементов представляет собой удельное потребление i -го продукта (услуги) в расчете на 1 денежную единицу стоимости валового выпуска продукции (услуги) j -го вида экономической деятельности ( i , j = 1,..., n ).

Таким образом, после качественных преобразований блока потребительского поведения домашних хозяйств непрерывный вариант открытой динамической межотраслевой модели региона (4) представляется в виде замкнутой динамической системы:

x ( t ) - Ax ( t ) - B dx ^ t ) - Gx ( t ) = 0 .                     (5)

dt

В дискретном балансе (при A t = 1) вектор инвестиционного спроса равен:

U ( t ) = B A x ( t ) = B [ x ( t + 1) - x ( t )] = B p x ( t ), где p - темп прироста продукции за период (год).

Тогда замкнутый динамический баланс имеет вид:

x ( t ) - Ax ( t ) - Gx ( t ) = B p x ( t ).

Объединив матрицу коэффициентов прямых затрат и матрицу удельного потребления домашних хозяйств, получим «интегральную» матрицу коэффициентов текущих затрат, равную A + G , которая в силу свойств матриц A , D и V является продуктивной и невырожденной.

Таким образом, после необходимых преобразований получаем следующие динамические уравнения:

x ( t ) - ( A + G ) x ( t ) = p Bx ( t ),

( E - A - G )^-1 Bx ( t ) = - x ( t ).

P

Обозначим: H = ( E - A - G ) ¹ B , 1 = — .

Р

Тогда, опустив обозначение времени, получим:

Hx = 1 x , ( H - 1 E ) x = 0.

Допускаем, что при ( E - A - G ) ^{- 1} >  0 в каждом ряду матрицы B есть хотя бы один положительный элемент. Тогда матрица H ₍ n _X n ) >  0 . При таком допущении согласно теореме Перрона-Фробениуса о положительноопределенных матрицах максимальный по абсолютной величине положительный характеристический корень 1 * матрицы H и правый положительный характеристический вектор x * определяются однозначно, то есть других неотрицательных характеристических векторов не существует. Определив темп прироста производства р = Д-, задаем начальное со- 1

стояние вектора валовых выпусков x ₀ и устанавливаем сбалансированную траекторию роста экономики региона (вектор { kx * : к >  0}).

2 Решение задачи по расширенной межотраслевой модели

Практические расчеты по расширенной межотраслевой модели в динамической постановке были проведены на основе реальных данных таблицы «затраты-выпуск» по 14 видам экономической деятельности. Путем процедуры агрегирования были получены оценочные данные в денежном выражении по трем укрупненным отраслям (секторам) экономики Республики Бурятия: 1) добывающие отрасли; 2) перерабатывающие отрасли; 3) прочие отрасли (в основном сфера услуг) ( i , j = 1,2,3; n = 3). Ввиду имеющейся пока ограниченности статистической информации данные по доходам и потребительским расходам домашних хозяйств представлены без их разбивки на отдельные группы ( q = 1). Кроме того, вектор капитала пока представлен без разделения на отдельные виды ( m = 1).

Исходные данные. Исходная информационная база в начальном периоде по трем секторам экономики республики включает оценочные значения технологической матрицы коэффициентов прямых затрат, матрицы капиталоемкости и удельных капитальных затрат, структуры потребления домашних хозяйств и нормы сбережения в качестве некоего управляющего параметра, существенно влияющего на накопления капитала и равновесный экономический рост.

Итак, исходная матрица коэффициентов прямых затрат A по трем секторам экономики получилась равной:

( 0,145

a (3 X 3) = 0,246

0,022

0,211

0,289

0,041

0,030 '

0,287 .

0,164 .

Матрица капиталоемкости f (в данном случае вектор-строка при q = 1) равна:

f (_M) = (1,39; 1,26; 0,87).

Матрица удельных капитальных затрат K (в данном случае вектор-столбец) равна:

K (_M) = (1,19; 1,28; 1,09) ' .

В целом для домашних хозяйств структура отраслевого потребления продуктов (услуг) в начальном периоде оценивается следующим образом: a ₁ = 0,11; a ₂ = 0,68; a ₃ = 0,21.

a ₁ + a ₂ + a ₃ = 1.

Для всех домашних хозяйств агрегированная норма сбережений оценивается как s = 0,184 , соответственно норма потребления в таком случае равна: в = (1 - s ) = 0,816.

Результаты расчетов. В результате расчетов матрица удельного потребления домашних хозяйств D (в данном случае вектор-столбец) составила:

D _(М) = (1 — s )( a ₁, a ₂, a ₃) ' = (0,090; 0,555; 0,171) ' .

Коэффициенты вектора V определяем, учитывая продуктивность технологической матрицы прямых затрат:

L a y < ^{1 (} j = 1,-, n ); v j = ¹ - L a, ⁽ j = I-, ⁿ ). I = 1                                                                        i = 1

В данном случае вектор V и соответственно матрица G = DV равны:

V (1 _X 3) = (0,587; 0,459; 0,519),

" 0,053  0,041  0,047 ^ Gnx = 0,326  0,255  0,288 (3 X 3)          J               J               J v 0,101  0,079  0,089 ;

, det G = 0.

Располагая теперь исходной матрицей коэффициентов прямых производственных затрат A и расчетной матрицей удельного потребления домашних хозяйств G , получим «интегральные» матрицы коэффициентов прямых и полных затрат:

0,198  0,252  0,077                  3,267  2,3722,161

,,,,,,

A + G = 0,572  0,544  0,575 , (E - A - G)-1 = 5,974  7,0846,065

_v 0,123 0,120 0,253 J                 ^ 1,493 1,524 2,665 ,

В инвестиционном блоке рассчитываем матрицу приростной капиталоемкости B = Kf :

" 1,654 1,499 1,035 ^Л

B = 1,779 1,613 1,114 , det B = 0.

_v 1,515 1,373 0,948,

Получив в результате замкнутый динамический баланс, рассчитываем матрицу H _{(3 х 3)}:

' 12,898 11,692 8,073 '

H = ( Е - A - G ) ^{- 1} B = 31,674 28,712 19,825 , det H = 0.

_У 9,18    8,56    5,769 ,

Таким образом, матрица H является вырожденной как и матрицы G и B , получаемые в результате перемножения двух прямоугольных матриц, в которых n = 3, q = 1, m = 1.

И тогда, решая характеристическое уравнение матрицы H : det( H - Л Е ) = 0, получаем характеристический многочлен матрицы H 3-й степени относительно ее собственного значения Л :

- Л ³ + 47,379 Л ² = 0.

Свободный член данного уравнения detH = 0 . Отсюда максимальное по своему модулю положительное значение Л* = 47,379 , а темп прироста производства р = 1 = 0,021106(2,11%) . Соответственно коэффициент Л роста к = 1 + р = 1,0211, а траектория сбалансированного роста экономики Республики Бурятия представляет собой вектор: 1,0211 x *, где x * = (x1, x 2, x 3).

Собственный вектор матрицы H найдем, решая систему линейных уравнений:

( H - 47,379 Е ) x * = 0, или

'- 34,5	28,7	5,8 '	' x 1 ^
31,7	- 45,8	14,2	x . 2	= 0
У 9,2	20,5	- 29,7 ,	У x 3 7

.

Полученная в результате фундаментальная система решений состоит из одного вектора:

x* = (1,000; 2,456; 0,715), а произвольный собственный вектор из множества H(Л*) равен:

wx * = ( w ; 2,456 w ; 0,715 w ), w e R .

Таким образом, при исходных данных получаем начальный собственный вектор в виде структуры выпускаемых продуктов и услуг в экономи -ке Республики Бурятия:

x ⁰ = (23,98%; 58,88%; 17,14%); x , + x ₂ + x ₃ = 100%.

При различных масштабах межотраслевой экономики региона (при различных значениях w) для базисного периода (года) рассчитываем в отраслевом разрезе как объемы валовых выпусков, так и все остальные производные показатели межотраслевого баланса региона : промежуточное потребление в первом квадранте, потребительский спрос домашних хозяйств и инвестиционный спрос во втором квадранте, структура вало- вой добавленной стоимости в третьем квадранте. В динамике на среднесрочную перспективу имеем возможность строить межотраслевые балансы для любого периода (года), располагая рассчитанным сбалансированным коэффициентом роста производства, в нашем случае равным k = 1,0211.

Заключение

Сравнительный анализ изученных динамических межотраслевых моделей с учетом экологических ограничений показал, что в теоретикометодологическом плане такие модели в виде системы линейных дифференциальных уравнений адекватно отражают непрерывный характер производственно-экономических процессов. Однако признается чрезвычайная сложность экспериментальных расчетов по данным моделям с точки зрения приближения их к реальности. Приходится учитывать объективно существующий дискретный характер отчетности экономических показателей за определенный период времени (месяц, квартал, год) и сопоставлять дифференциальные и конечно-разностные уравнения при различных вариантах отражения показателей инвестиционного блока.

Установлена чрезмерная открытость базовых моделей межотраслевого баланса, снижающая самостоятельную значимость и системность модель -ных расчетов. Так, в уравнениях (3) и (4) траектории потребления домашних хозяйств экзогенно определяются одинаковым постоянным темпом прироста для вектора потребительских расходов. Считается целесообразным снижать долю экзогенных величин до уровня некоторых управляющих параметров и добиваться максимальной эндогенизации переменных для углубления системного анализа региональной межотраслевой экономики.

В данной работе проблема снижения уровня открытости динамической межотраслевой модели решается путем структурной увязки вектора потребления домашних хозяйств с их доходами, а доходов — с региональной производственной деятельностью. Предлагается закрытый вариант динамической межотраслевой модели региона, максимально приближенный к дискретной реальности экономической динамики, обеспечивающий более содержательный и системный анализ межотраслевых связей в регионе.

На основе реальных данных таблицы «затраты-выпуск» по Республике Бурятия проведены экспериментальные оценочные расчеты прямых и полных затрат, коэффициентов инвестиционного блока и матрицы потребительских расходов, взаимосвязанной с региональными доходами и валовыми выпусками. На основе выведенного характеристического уравнения матрицы замкнутого динамического межотраслевого баланса рассчитан собственный вектор валовых выпусков в республиканской экономике и определена траектория сбалансированного экономического роста на среднесрочную перспективу.

В дальнейших исследованиях с уточнением управляющих параметров, технологических, инвестиционных и потребительских коэффициентов на основе разработанной в работе модели предполагается постановка макроэкономической задачи оптимального управления с максимизацией дисконтированного суммарного потребления в качестве целевой функции.