При формировании цифрового кода возникает шум квантования. Характеристика формирования шума квантования изображена на рис. 1. Этот шум складывается с обрабатываемым сигналом.

Любая излучающая (принимающая) антенна радиосигнала, так же, как и любой приемопередающий датчик (в случае ультразвукового сигнала), в силу условий его физической реализуемости, имеет боковые лепестки диаграммы направленности. По ним может приниматься сигнал от побочного (неинформативного) импульсного объема, расположенного на той же дальности, что и исследуемый импульсный объем, находящийся в створе главного лепестка, но расположенный под другими углами азимута и места. В нем могут быть отражатели, совокупность которых в тексте работы и называется отражающей доминантой. Квантуется сигнал, отраженный от капель дождя (от однородной и изотропной среды), в смеси с сигналами отражающих доминант. Таким образом, эхо-сигнал есть нормальный случайный процесс с математическим ожиданием m = m ( t ) .

координат вектора п = ( п , П ) в шум квантования

Сущность математической модели

При формировании эхо-сигнала складываются: центрированный нормальный случайный процесс эхо-сигнала дождя с детерминированной, повторяющейся вдоль развертки во времени сферической координаты дальности при повторяющихся угловых координатах главного лепестка, функцией m = m (t). Она имеет место вдоль сферической координаты дальности и вызвана отражающими доминантами, эхо-сигнал которых принят по боковым лепесткам. Плотность рас- пределения вероятности вектора, являющегося результата сложения сигнала метеоэхо и сигна- лов отражающих доминант имеет вид:

1 ( x i- m ( t ) ) ² - p n ( t ) ( X i— m ( t ) )( x 2- m ( t + t ) ) + ( x 2- m ( t +t ) ) ²

^{2 7} ( ¹ - р П ( ^t ) )

⁷ 2 ( ^{1 -} P 2 ^{( t} ) )

где x ₁ , x ₂ - значения координат вектора n ( п₁П ₂ ) в моменты времени t ₁ и t ₂ ; < 7 ,2 — дисперсия

значений координат x ₁ и x ₂ вектора fj(п₁,П ₂ ) ; m ( t ) - математическое ожидание координат вектора П ( п₁П ₂ ) ; Л = ( /ft, n ₂ ) = n + ^ ; n = ( n₁,n ₂ ) - вектор теплового шума приемника; § = ( ^₁,^₂ ) - нормальный вектор эхо-сигнала от облачно-дождевой системы. Здесь о^ = о^ = а^ информативные величины, необходимые для формирования оценок K w , а затем о и е . Р п ( т ) -

коэффициент корреляции координат г] ₁ и г] ₂ . т = t ₂ - t₁ - шаг дискретизации.

Так как m = m ( t ) неслучайная функция, повторяющаяся от зондирования к зондированию, то обозначим m ( t ) = m ₁, а m ( t + т ) = m ₂ формулу (1) перепишем с учетом этих обозначений:

_ 1 ( ^x 1 ^{- m} 1 ) ^{2 -} P n ( ^t )( ^x 1 ^{- m} 1 )( ^x 2 ^{- m} 2 ) ⁺ ( ^x 2 ^{- m} 1 ) ²

1                 ^{2                 7} 2 ( ^{1 -} P - n ^{( t} ) )

e

2n7 (1 - py, (t ))

Из определения шума квантования [2] известно, что вектор шума квантования есть разность

векторов Z = П - X , где п - входной вектор алгоритма квантования, и х выходной квантован

ный вектор. На рис. 1 видна периодичность функций ^ ( x^ ), формирующих шум квантования с периодом А . Учитывая их «периодичность» разложим в ряд Фурье функции ^ ( x j -).

Математические преобразования

Выполним математические преобразования аналогичные преобразованиям, проделанным в работе [1], но с той разницей, что квантуемый сигнал в данной работе имеет не центрированную плотность вероятности, описываемую выражением (2). Из [2] известно разложение периодической функции v ( x j ) (см. рис. 2) в ряд Фурье:

V(xj) =“Л^^sin—— xj , n n=1  n       А где j = s, c – синфазная или квадратурная составляющая комплексного сигнала.

Характеристическая функция вектора г) = (п₁,Р ₂ ) (см. [2]) имеет вид:

= J J e ' C ' i ^ C ^{x 1} ) ■ ' .'- ' ^{x 2} ) ) _ж_ ₍ x ₁, x ₂ ) dx₁ dx ₂.

-X - J

Здесь i - мнимая единица, а M {} - символ математического ожидания.

Разложим периодические функции e^{( &V (}- ^{x 1))} и e^{( 9} 2 ^{V ( x 2))} в ряды Фурье:

X e⁽^ 1 . ^{( x} 1 )) = _E   C 1 n

n1=-X

e innw ^{( x} i )

X e<^(x2)) = s c2n n 2 =-J

e in 2 2 ⁿ v ^{( x} 2 )

Здесь А играет роль периода, а функции у(x ₁) и у ( x 2 ) на каждом из отрезков линейности

--- 2,  2

длиной А, изображенные на рис. 1, есть периодические куски прямых линий:

У ( ^x 1 ) = ^x 1 , У ( ^x 2 ) = ^x 2

в центре системы координат z 0 x и смещенные по оси z в зависимости от текущего значения

^xj ^.

После подстановки у(x ₁), у(x 2 ) в (5) и(6) разложения примут следующий вид:

TO        J

e^{( 9}x_V ⁽ x ¹)) = z   С 1 п-

i in i 2 n x i

,

TO e< ^{9 (} x 2 )) = z c 2 п

'п 2 2 n x 2

.

Коэффициенты разложения функций e i ^{( 9 1 V ( x 1))} и e' ^{( 9} 2 ^ ^{( x 2))} (см. [2]) есть интегралы:

c l п

¹      2 e ⁱ

in12лx1         sin I 3, i9 x e                 V

* ^{1 1}------ dx = —^—

—

—

c 2 n =

1 A

1    _{2 e}

'п^ 2nx^

i9 x eT

' 2 2

A

—

2пп ₂ А

,

—

2пп ₂ А

J 2

.

Подставив формулы (10) и (11) в (8) и (9), а результаты подстановки в (4), перепишем (4) в следующем виде:

TO TO

If X

—TO —TO

TO

• (^   2пп, jA sin И    \   2 ein12пx1

z

а ^J 2 e

, in ₂2 nx 2

Wn ( x₁, x ₂ ) dx₁ dx ₂.    (12)

Изменив порядок суммирования и интегрирования и оставив под знаком интеграла только выражения, зависящие от переменных интегрирования, получим иной вид выражения (12):

_m sin И ¹ — TO            1 Л О

TO

z

п 2 =—TO

TO TO

ff

—TO —TO

'п2 2nx ₂   in ₁2 пx ₁

——Wn ( x₁,x ₂ ) dx₁ dx ₂ .(13)

Вычисляя интеграл формулы (13), являющийся интегралом преобразования Фурье, подставив формулу (2) вместо Wn ( x₁, x ₂ ) , получим (см. [2]) следующий вид этого интеграла:

TO

f

—TO

in ₁2пx₁ ^п 2 2nx ₂

A    2пО2 (1 — pl (T ))

1 ( x 1 ^{— m} 1 ) ²

2 e

p — n ( ^T )( x i ^— m i )( ^x 2 ^— m 2 ) ^— ( ^x 2 ^— m 2 ) ²

^ 2

dx₁ dx ₂ =

.f  п 2п п 2п i mi ——+m^ —

V А      А

= e

| ⁺ P n

.

После этого искомая характеристическая функция (13) вектора ζ примет вид:

. / „   2nn, 1A sin 51 —

¹ A 2

Ф ⁽ A, j ⁵ ) = ^£ "Г    pn. A A

w

I

2nn ₂1A

A ) 2

xe

/ п 2.П     п₂ 2.П 1 1

i m i ——+ m —— —

I ¹ A      ² A ) 2

₂ [ Па 2.П |            \  ₂ [ Па 2П I [ П т 2 п

■’ I ^^) ^{+ р} п ^{( т ) ст} » I ^г)1

₂1 п 2 2п

I A

))

.

Плотность распределения шума квантования есть обратное преобразование Фурье (см. [2]) выражения (15):

,   w w w

W ^{( 2 , 1} Z 2■^)- - J J £

( ^{2 n} ) —w—w П 1 =—w

sin I 5 1 ^—

2 nn ₁1A

A

xe

(   ni 2n     nn 2n i I ml ,  + m 2 2

I     A        A

-

2пп₁ A

) 2

A

w

-

2 nn ₂ 1A

A ) 2 2 nn ₂1A

A ) 2

I ⁺ Рп ^{( т ) o} "7

^x e i ^{( 5 1 Z 1 + 5} 2 ^Z 2 ) d^ d^  ¹ z i| ^-A ; ¹ z 2| ^-A .

Из вида функций z₁ = v ( x₁ ) , z 2 = V ( x 2 ) изображенных на рис. 1, следует, что область опре-

деления функции (16) есть: | z j -у и

I z ₂1 - ~. Это обстоятельство и учтено в формуле (16). Из-

менив порядок интегрирования и суммирования, оставив под знаком интеграла множители, зависящие от переменных интегрирования, перепишем (16) иначе:

1      w    w

Wz ⁽ z 1 , z 2 ) = —2 £ £ exp

( ^{2 n} ) n 1=—w n 2 =—w

^с П

п 2п 1 2

A

+ Рп ( ^т И

n ₁2 n V in 2 2 n

A

A

₂/ n 22 n ^п CA^-

x

(    n i 2 n     n-> 2 n 1

xei Im    + m 2~d w w xf J

—w —w

sin I 5 1 ^—

2пп₁ 1 A

A

—

2 пп ₁ A

) 2

-— x

A

—

2 nn ₂ 1A

² I

AjL k x e- ⁱ⁵ z .+^ z ² ) d9 1 d3 2 ; | z ,| < A; | z 21 < A•

2 П n । A                              2       2

A ) 2

Обозначим интеграл в формуле (17) как I ₁ . Тогда подынтегральное выражение формулы (17) есть произведение множителей с независимыми переменными и I будет иметь вид:

w sin I 5 1 —

2пп₁ 1A

A

—w

—

2лп1

A

I 9               w

ZZ- e ^{— 5} z ¹ d5 x J

-            —w 2

—

2 nn ₂ 1A

^A/2 e " ⁵ z ^{2 d} » 2 ;| z dz2I¹⁸)

2nn 2 I A                  2       2

A ) 2

В интегралах(18) сделаем замену переменных A x 1/2 = A 5 /2 — nn и A x 2/2 = A 5 2/2 — пп 2 . Тогда dx₁ = d5 , 5 = x ₁ + 2пп 1 /A, dx ₂ = d3 2 , 5 2 = x ₂ + 2 nn ₂/A и (18) примет вид:

J — i ², ^— i ^{2 п п}1 z 1    i ^{2 п п} 2 z 2 f sinC^{A x} 1/ 2L ^— 1

¹ =                   — ^J w   ( A x 1/ 2 )

^w sin ( A x 2/ 2 )

—w

( Ax 2/2 )

e ^{— ix 2} z ² dx 2 .

Характеристическая функция (см. [2]) одномерного равномерного W (ф) = — закона рас-фХ     a пределения случайной величины ф на интервале [a,b] имеет вид:

iibS   „— ibS ф     e------ ф (  )   iS(a —b)

Тогда для нашего случая имеем, что [ a,b ] = A, a = ^ , b = — ^

.

i ^{A S aS}       f A S 1   _ . f A S

.ibs  „iibs       3              — 12sin|

C._x e — e       e 2 — e 2          | 2 J| zS) —    -     ~. —               ——

’ iS( a — b)         iSA           iSASA

.

Нетрудно заметить, что интегралы в (19), дополненные множителями 1/2п с точностью до знака функции (21), это обратные преобразования Фурье. Выражение «характеристическая функция равномерной плотности распределения» следует понимать лишь в контексте промежуточного преобразования. Результат вычисления обратных преобразований Фурье (19) примет вид:

( 2 п ) ² — _z 2^ — _z 2 5 5 2 5 2        a ,   , A

1 1 =          ^{e A e A} ;| ^z 1l “ 2^{; 1 z} 2I “ 2.

Искомая плотность распределения после подстановки I (22) в формулу (17) примет вид:

f n 2 n n ₂ 2 n 1

, да да    i | ^mV^T + ^m2      I

ZZ ( z 1 , z 2 ) = J2 EE e ^{1 A      A J}x

^A   n 1 =—да n 2 =—да

^— 2 x e

2 [ П 1 2 n 1         , x 2 [ n , 2 n if n 2 2 n 1      2 [ n 2 2 n 1

+ Pfi Г ) ^ 7                + ^ 7

¹¹1 A j - ■        I A JI A J 4 A J

2 n n₁ z₁   2 n n ₂ z ₂

^{X - A - A}     z i| “^A ; z 2| “^A

.

Для удобства дальнейших преобразований формулу (23) перепишем следующим образом: z       x      1    -да   -да    ^— i 2 ^ ( n i ( z i ^— m i ^{) +} n 2 ( z 2 ^— m 2 ) )

Zz ^{( z} 1 , ^z 2 ^{) =} T2 EE ^{e A                x}

^A   n 1 =—да n 2 =—да

2 x e

₂ f n 2 n 1        / x ₂f n 2n if n 2 n 1     7

-I          I  ⁺ Pn ^{( r )cr} 2 I          II          1 + ^CTn

n 2 2 n 1 2

A

Л i A , , A ^J ; I ^z 1| “ у; । ^z 2I “I

.

Учитывая нечетность функции sin( x ), выражение (25) перепишем иначе:

2 x e

, да      да

W_? ( z i , ^z 2 ) = -y £   £ cos

^A n =—да n ₂ =—да

z ₂

—

₇ f n 2 n 1          , x fl n , 2 n if п_э 2n 1 f

2 1       I ⁺ Pn ^{( r} ) ^ -1       II        I ⁺ ^-

m ₂

n 2 2 n 1 2

A

z ₁

—

x

Л I A , , A ^J ; ¹ z il “ у; I z 2I “i

.

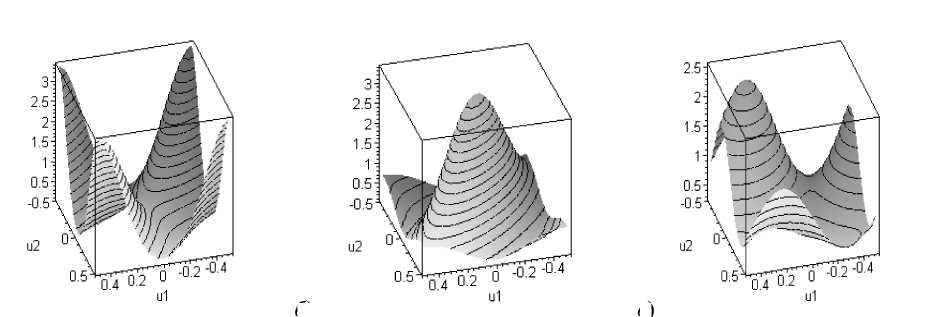
Графики W^ ( z₁, z 2 ) (25) (см. рис. 2) построены для различных значений т₁ и m ₂

и для оди-

наковых Р п ( т ) . Список параметров процедуры proc( t , . . u 2) пакета Maple: t, rho, ml, m2, ul, u2.

A 2                             2 _П 2

–

Здесь ml = m_h m2 = m₂, rho = p ( r ) , z_x = ui, z ₂ = u 2 , в = — - глубина квантования, t =---

1         2        -^    1       2           ^                                в вспомогательный параметр.

При т₁ Ф m ₂ график не симметричен (рис. 2, в ). Вектор математического ожидания плотности (показано ниже) в общем виде всегда имеет нулевые координаты М^ = ( М^_рМ^ ₂) = ( 0,0 ) при любых Шу и m ₂ . Заметим, что равенство m = m ₂, не является достаточным условием симметрии графика плотности как может показаться из рис. 2.

а )

б )

в )

Рис. 2. Плотность распределения шума квантования при различных m и m . Здесь а) это плотность распределения при proc(1,3, 0,7, 0,5, 0,5, u1 ,u2), б) плотность распределения при proc(1,3, 0,7, 0,0, 0,0, u1, u2), в) плотность распределения при proc(1,3, 0,3, 0,3, 0,75, u1, u2)

Статистические характеристики двухмерной плотности вероятности шума квантования

Вычислим векторы математического ожидания    М^ = ( М^ _р М, ₂) и дисперсии

D^ = (D^pD^2) для плотности (26). Разобьем индексы суммирования в формуле (25) на девять групп и запишем ее в виде суммы девяти сумм:

W^ ( z 1 ,z ₂ ) = S 1 (n 1 = 0, n ₂ = 0 ) + S ₂ ( n 1 = 0, n₂ eZ + ) + S 3 ( n 1 eZ ⁺ , n ₂ = 0 ) + S 4 ( n 1 eZ ⁺ , n ₂ eZ ⁺ )

+ S 5 ( n 1 = 0, n ₂ eZ ) + S 6 ( n 1 eZ , n ₂ = 0 ) + S 7 ( n 1 eZ , n ₂ eZ ) + S 8 ( n 1 e Z⁺, n ₂ eZ ) + S 9 ( n 1 eZ - , n ₂ eZ ⁺ )

где

^S 1 ( ⁿ 1 = 0, ⁿ 2 = ⁰ ) = ^2

S ₂ ( n₁ = 0, n ₂ eZ ⁺ ) =

ад "

^1 2 5 '

n 2 =1

• 1    J n₉ 2n I

a2

• 2  ¹ A J     2 п    A./2 п I

cos     n2z2 cos     n2m2;

kA      J I AJ

S 3 ( n₁ e Z⁺ ’ n ₂

ад

= ^{0 )} =A n 5

ад

1  ₉f n 12 n V

- 2^ ⁿ t a _v

e

f 2n )    [ 2 n      )

cos I — n₁ z 1 I cos I — n₁ m₁ I;

I A     J   I A     J

S 4 ( n 1 e Z⁺, n ₂ e

ад ад z>£ 55

n =1 n₉ =1

1 —

2 e

₉ f n 2 n ]     _{z x} Д n , 2 n if n 2 n

” ⁿ I Vr ^p n ^{( T ) O} 2 1

/       \ 2 ^

₂1 n ₂2 n ] ⁿ I "T" I

X

^S 5 ( ⁿ 1

X cos

- ^m ₂ ) ) + ( ⁿ 1 ( ( z 1 - m 1

ад "

= 0, n ₂ eZ - ) = -    ^e

’ A ² n 2 =1

—

2 ⁿ

2 n 2 2 n । "T" I

f 2 n T.J 2 n I cos I — n ₂ z ₂ I cos I — n ₂ m ₂ I;

kA      J k A       J

S 7 (

п1 еХ , п ₂ е

—

12 Е = ^А п 1 =1

—

да да      2

А 2 Е Е e '

° 2|

^п 1 =1 ^п 2 =1

х cos

z ₂

—

- ^ 21

п 1 2п

п 1 2п

—

m ₂

cos

+Рп (т)°п

п 1 2п

;

п ₂ 2 п

п

;

п ₂ 2 п

⁷ х

S 8 ( п 1 е Z+, п ₂ е

1 да да

Х2 ЕЕ e ^А   п 1 =1 п 2 =1

°2

п 1 2п

—Рп Т)°п

п 1 2п

п22п

п ₂ 2 п

п

х cos

z ₂

—

m ₂

;

—

п 1 2п

S9 (

п1 еХ , п ₂ е

Z + ) =

да да      2

А 2 ^ЕЕ e ¹

п

—Рп (г)°п

п 1 2 п

п ₂ 2 п

п ₂ 2 п

2 ^

п

xcos

n i = 1 П 2 = 1

z ₂

—

m ₂

Объединяя совпадающие слагаемые: (28) с (31), (29) с (32), (30) с (33) и (34) с (35) получим:

2 Е

—

+2 Е Е

1+2 Е

- ° ²

п 22д

—

e

^п 1 =1

—

° ²

e

^п 1 =1 ^п 2 =1

+2 Е Е

e

cos

^п 1 =1

- °2

п 1 2п

cos

xcos

—

° ²

e

п 1 =1 п ₂ =1

х cos

п 1 2п

п 1 2 п

z ₂

—

+ Рп (т)^2

п 2п

п22п

п ₂ 2 п

п

z ₂

—

m ₂

п 2п

п ₂ 2 п

п ₂ 2 п

п

m ₂

По определению значения координаты M (см. [2, 3]) можем записать:

да да

MZ 1 ^— J J z i Wz ( ^z 1 , z 2 ) ^dz1 dz 2 =

—да —да

— -1 Z I- —

A ^{2 Z}   A ²

A

A A

да

J J ^ 1 11+2 Z n1 —1

e

A A

- 2 - 2

1 n 2n I

2 4 A J < 2 n    )   < 2 n Y

■    ^x     ' cos —n ₂ z ₂ cos —n ₂ m ₂ +

I A      J I A       J

1 J n 2n I

/Г21

n II

E2     A        ( 2n     ]   । 2n]

e    v    ; cos —nZ1 cos —n m1

V A J I A )

n — 1                       X        7 X7

1    ₂ ( n 1 2 n

^ 7

да да 2

+2 Z Z e I

П 1 —1 n 2 —1

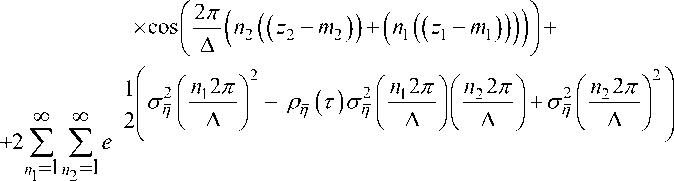
^— m 2 ) ) ^— ( n 1 ( ( z 1

xcos

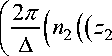
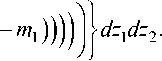
Изменяя порядок суммирования и интегрирования в слагаемых суммы (37) после вычисления простейших интегралов, получаем: 1 ₂ — 0, 1 3 — 0 и 1 4 — 0 .

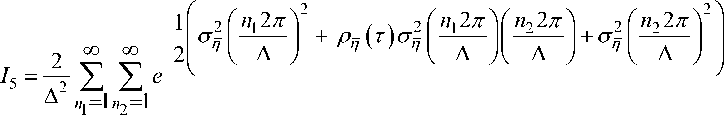
A   A

J ^d z 2 J —A  —A

z ₁ cos

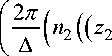
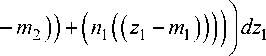
— 0.

„ да  да

1 6 — 27 Z Z

^A « 1 —1 n 2 —1

2 e

n

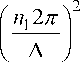
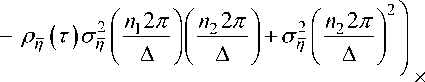
A , A< x J dz2 J z1cos I — ( n2 (( z2

A   A

—2

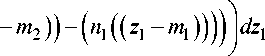
—0.

Повторные интегралы в выражениях I ₅ и I ₆ содержит по восемь слагаемых, каждое из которых содержит нулевой интеграл-множитель и поэтому I ₅ — 0 и I ₆ — 0. В результате M^ 1 — 1 ₂ + 1 3 + 1 ₄ + 1 5 + 1 6 — 0. Аналогично М^ 1 получаем М^ ₂ — 0 и M^ — ( M^ i , M^ ₂ ) — ( 0,0 ) .

Квантование с округлением до ближайшего целого не смещает квантуемую амплитуду сигнала или данных (в отличие от других видов квантования).

Из [2, 3] известно, что значения координаты D вектора D для двухмерной плотности

• (25)    вычисляются по формуле:

DZ 1 ^— i J ^z W ( ^z 1 , ^z 2 ) ^dz1^dz 2 ^—

• ^— 2 ^— 2

  A ²

  
  

  A A

  
  

  да

  
  

  J b-1 1'2 Z.

  
  

  A A

  
  

  n ₂

  
  

  =1

  
  

  1    , n₂ 2n 1

  — ^ 2

  2 ^7| A ^J     ,2 n    1   ,2 n

  e              cos      n ₂ z ₂ cos     n ₂ m ₂

  I A      J I A

  
  
  
  
  
  

  да

  +2 Z

  / /| — 1

  
  

  e

  
  

  • 1   J, in 2n 1

  — ^n l           I

  • 2 ^7| A J     ,2 n    1   ,2 n

  ■               COS| — n 1 ^z1 I COS| — n 1 m 1

  I A     J I A

  
  

  да

  
  

  да

  
  

  +2 Z Z

  n —1 n 2 —1

  
  

  2 e

  
  

  n

  
  

  n 2n 1 2

  
  

  A

  
  

  ⁺ Pn ( ^T ^n

  
  

  n 1 2 n Y n 2 2п

  
  

  A

  
  

  A

  
  

  ₂, n ₂ 2 п 1

  ⁿ 1“ J

  
  

  x cos

  
  

  z ₂

  
  

  —

  
  

  m ₂

  
  

  z ₁

  
  

  —

  
  

  m ₁

  
  

  да да

  +2 Z Z e n — 1 n 2 — 1

  
  
  
  

  n

  
  

  n 2 n 1 2

  
  

  A

  
  

  ^— Pn ( ^T ) %

  
  

  n_x 2п Y n 2 2 п

  
  

  A

  
  

  A

  
  

  ₂, n 2 2п 1

  '        \ J

  
  

  cos

  
  

  z ₂

  
  

  —

  
  

  m ₂

  
  

  z ₁

  
  

  —

  
  

  m ₁

  
  

  12 Z 1 2j .

  ^A j — 1

  
  
  
  

Вычислим сумму (40), обозначив ее слагаемые как I ₂₁, I ₂₂, I ₂₃, I ₂₄ и I ₂₅ . В результате вычисле-

A ²

ния простейших интегралов получаем I₂ ] — — и / ₂₂ — 0•

Изменяя порядок суммирования и интегрирования, вынося за знаки интегралов множители, не зависящие от переменных интегрирования в I , I ₂₄ и I , получим:

1  , n 2n 1

^ 2   ¹

^A 2 n —1

dz ₁.

^A n —1 n 2 —1

n

n 2 n 1 2

+ Pn (T )°2

n 1 2n Y n 2 2 n

₂, n 2 2 п 1

J J

z ₁ ² cos

z ₂

—

m ₂

z ₁

—

m ₁

— 0.

э од од 2

1 25 = ^ A A ⁶

^A n^ =1 n ₂ =1

n

X

A A

j  j z12cos

A A

z ₂

—

m ₂

z ₁

—

m ₁

: 2 = 0.

Вычисляя интеграл выражения I

выполним замену переменной вида

x =

2 nn 1 z 1

A ^;

x A z 1 =----- 2 nn 1

,   2nn dx =----j

A

- dz 1 ; x_B = ПП 1 ; х н = —nn 1 :

_ A ^  12 ⁿ

²³ "4 ( n ) ³ n ^A 1 ^ e

in1 2n Y a,

( 2n cos    n m

I A ¹¹

A    nn dz x2 cos xdx.

A   —nn

Воспользовавшись очевидным соотношением:

j x ² cos xdx = 2 x cos x + ( x ² — 2 ) sin x + C

и учитывая, что sin nn = 0, значение внешнего интеграла в (44) равно A, и то, что множитель cos ( nn ) есть чередующаяся последовательность +1, где знак «-» - соответствует нечетным n , а

«+» – четным, то получим следующий результат:

I 23 =

A

^{( п ) 2}

да , a 4 n =1 ⁿ

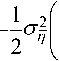
2 n 1 2n

cos

A

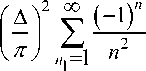
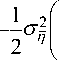
2 n 1 2n ""A",

f 2n cos    n m

I A ¹¹

( A ) ² f ( —1 ) "'   ,, ²

/ X2 ^A /  \2 q

( ⁿ )   n 1 =1 ( n 1 )

f 2nj cos

I A

где

2 n ²

q = e "  t = e ^e .

Повторный интеграл выражения I ₂₄ является сумой восьми выражений, каждое из которых имеет нулевой интеграл-множитель. Аналогично выражению I ₂₄ формула I ₂₅ также является суммой из восьми выражений, каждое из которых содержит нулевой интеграл-множитель. Следовательно 1 ₂₄ = 1 ₂₅ = 0. Окончательно сложив 1 ₂₁ , 1 ₂₂ , 1 ₂₃ , 1 ₂₄ и 1 ₂₅ получим значение D^ 1 :

n         I - A²

DZ 1 = I 21 ⁺ I 23 = |2 ⁺

A

n

1 2 v( —1 ) n 4 f 2 n    j

I AТ4Гq  cosI 4Tnm1 I• n=1 (n)          V A     J

Выражение для d z ₂ с точностью до номера индекса m₂ совпадает с выражением (48).Таким образом, окончательный вид вектора второго начального момента следующий:

^D Z = ( DZ 1 , DZ 2 ) =

A 2 + ^fA) ² ±(—1)1 q n ²

12 I n J fl ( _n ) ^{2 4}

2.Я

A ² fA?

cos I a ^nm i I; 12 +1 n

n

^{( n ) 2}

n2    f 2n q cos    nm

I A ²

. (49)

Основные выводы

Из выражения (49) видно, что значения координат вектора второго начального момента для двухмерной плотности шума квантования зависят от величин математических ожиданий m и m квантуемого нормального двухмерного вектора (2). Значения координат второго начального момента в свою очередь являются информативными величинами в радиометеорологии и содержат интересующие физические величины. Тогда вторые члены в суммах в (48) приводят к смещению оценок значений координат этого вектора из-за присутствия величин m и m . Например, в радиометеорологии D (см. [5]) несет информацию о наведенном дипольном моменте Kw капель дождя, затухании радиосигнала туда и обратно на трассе распространения/(r0,Kw,to), интенсивности дождя R и водности облачно-дождевой системы M.

Для физической реализуемости высокоточных измерений заключающейся в формировании несмещенной и состоятельной оценки Dˆ с последующим вычислением оценок Kˆw , /(r0, Kw,to), RR и У, необходимо избавиться от второго слагаемого в выражении (49), так как шум квантования по мощности (не когерентно) складывается с сигналом дождя. Ранее было показано (37)–(39), что значения координаты вектора Mζ равны нулю при квантовании с округле- нием до ближайшего целого. По этой причине оценки mˆ 1 и mˆ 1 могут быть вычислены с требуемой наперед заданной точностью, но с физическим ограничением на интервал времени пока величины Kw , / (r0, Kw, to), R и M можно считать постоянными. В этом случае, очевидно, что для ˆ оценки Dζ будет иметь место следующее выражение:

ˆ

Га² а »(- 1 ) )

[12 I п) я () )2

q ^{n 2}

Г 2п  „ cos    nm

I А ¹

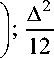
Mq) 2

) = 1 ( ) )

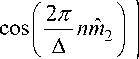
Наконец, поскольку дисперсия квантованного сигнала, согласно теореме о дисперсии [см. (4)] суммы есть величина:

DX = Dn + Dz + 2n KZ  ,’ j = 1,2;(51)

< jj где

Dy = Dr + Dn . л      z

Тогда, заранее вычислив оценки mˆ и mˆ , легко избавиться от вторых слагаемых в выраже нии (51) что и позволит сделать искомую оценку D [$i ] несмещенной и состоятельной при апри-ˆˆ орно известной величине А и апостериорных, не смещенных, состоятельных оценках Dn и D^ , вычисление которых на практике не вызывает затруднений с помощью алгоритма выборочного второго начального момента. Материалы работы важны при организации высокоточных измерений в связи, медицине, радиометеорологии и других областях науки и техники.