Модель СМО с неоднородными заявками и абсолютным приоритетом обслуживания

Одна из основных задач специалиста в области информационных систем и прикладной информатики – принимать обоснованные решения с целью повышения эффективности работы экономического объекта. Одним из наилучших способов обоснования решения является построение и анализ имитационных моделей, описывающих некоторые процессы функционирования предприятия. Функционирование предприятий торговли, производства может быть описано с помощью моделей систем массового обслуживания. Существуют две разновидности моделей СМО: аналитические и алгоритмические. Аналитические не учитывают полностью действие случайных факторов и поэтому могут использоваться как модели первого приближения. С помощью алгоритмических моделей исследуемый процесс может быть описан с любой степенью точности на уровне его понимания постановщиком задачи.

1. Концептуальная модель

Автором статьи разработан имитационный алгоритм функционирования СМО с заявками двух приоритетов. На вход системы поступают два потока заявок: высшего и

Пермская государственная сельскохозяйственная академия

Россия, 614990, Пермь, ул. Петропавловская, 23

низшего приоритета. Оба потока являются простейшими, т.е. время между соседними заявками имеет показательное распределение. Среднее время между соседними заявками для обоих приоритетов заданы, время обслуживания заявок – величина случайная, имеющая равномерное распределение с известным средним временем обслуживания и диапазоном изменения времени обслуживания. Все перечисленные характеристики случайных величин – входные параметры модели. Также входными параметрами будут период функционирования системы и число случайных реализаций.

Правило облуживания соответствует дисциплине LIFO ( абсолютный приоритет ) и состоит в следующем: если в канале обслуживается заявка низшего приоритета, то поступившая заявка высшего приоритета немедленно вытесняет её (занимает её место), после окончания обслуживания заявки высшего приоритета может быть произведено "дообслуживание" заявки низшего приоритета, однако её может вытеснить новая поступившая заявка высшего приоритета.

Выходными параметрами являются:

• •    среднее число поступивших заявок для обоих приоритетов;

• •    среднее число обслуженных заявок

  © Шимановская М. В., 2013                      ^обоих приоритетов.

2.    Моделирование

На основании этих показателей легко может быть введён критерий эффективности работы СМО, например средняя ожидаемая прибыль .

При моделировании использовался подход поэтапной последовательной проводки заявок [1]. В соответствии с ним сначала рассматривается изолированный поток заявок высшего приоритета так, как будто заявок низшего приоритета не существует. На этом этапе формируется массив из времён поступления заявок высшего приоритета, а затем эти заявки обслуживаются (формируется массив времён окончания обслуживания заявок высшего приоритета). Затем следует этап моделирования заявок низшего приоритета в условиях, что на временной оси уже располагаются обслуженные заявки высшего приоритета. Следовательно, заявки низшего приоритета могут занимать только свободные промежутки времени.

При взаимодействии заявок двух различных приоритетов могут возникнуть 3 возможные ситуации:

Ситуация 1. Ни одна из имеющихся заявок первого приоритета не препятствует обслуживанию заявки второго приоритета.

Ситуация 2 . Система приняла к обслуживанию заявку низшего приоритета, и она начала обслуживаться. Но до окончания расчётного времени обслуживания поступила заявка высшего приоритета, которая вытесняет данную заявку низшего приоритета. В этом случае необходимо рассчитывать время дооб-служивания заявки и вновь анализировать ситуацию.

Ситуация 3 . Заявка низшего приоритета поступила в момент, когда канал занят обслуживанием заявки с высоким приоритетом. Тогда нужно "сдвигать" время обслуживания заявки с низшим приоритетом.

Сложность моделирования процесса обслуживания заявок низшего приоритета состоит в необходимости учитывать, что обрабатываемая заявка может оказаться в одной из перечисленных ситуаций. Причём в случае сдвига времени обслуживания требуется обслуживанию какая-либо заявка высшего приоритета, т.е. в какую именно из перечисленных ситуаций попадает пересчитанное время обслуживания. В итоге заявка будет обслужена до конца, либо истечёт время функционирования системы, и заявка покинет систему необслуженной (так же, как и все последующие заявки второго приоритета).

Эта необходимость возврата к анализу ситуации реализована в [1] операторами безусловного перехода, что усложняет читаемость алгоритма и не соответствует принципам структурного программирования.

3.    Блок-схемы модели

Формирование заявок обоих приоритетов происходит по одному алгоритму (см. рис. 1). В результате работы процедуры заполняется массив из времён поступления заявок в систему Tz (время имеет показательное распределение), а также рассчитывается число поступивших заявок Nz. Выход из алгоритма происходит, если модельное время T превысит период функционирования системы Tkon.

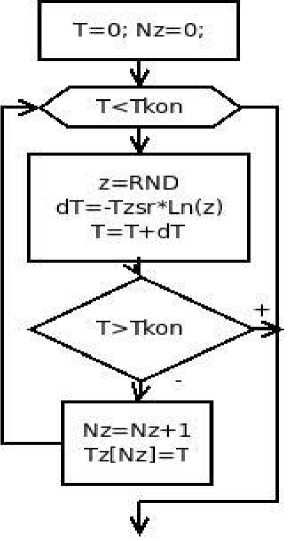
Рис. 1. Процедура формирования потока заявок.

Процедура обслуживания заявок высшего приоритета описана на рис.2. В начале процедуры обнуляется время освобождения канала обслуживания и число обслуженных заявок высшего приоритета.

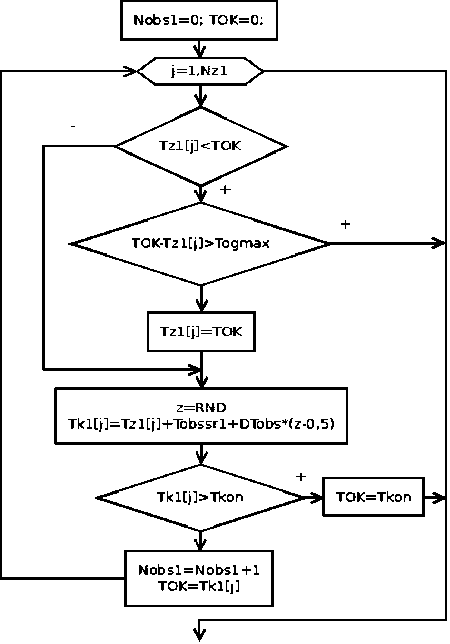
Рис. 2. Процедура обслуживания заявок выс- шего приоритета

Затем в цикле перебираются заявки (их число равно Nz1) и прежде всего проверяется, свободен ли канал. Если канал занят, то рассчитывается время ожидания заявки в очереди. Если оно превышает критическое Togmax, то заявка покидает систему необслуженной. В противном случае время начала обслуживания приравнивается ко времени освобождения канала TOK.

Далее с помощью генератора случайных чисел рассчитывается время окончания обслуживания данной заявки и записывается в массив Tk1. Если заявка успела обслужить-ся до окончания функционирования системы, то число обслуженных заявок высшего приоритета Nobs1 увеличивается на 1 и время освобождения канала приравнивается Tk1[j].

Более сложен алгоритм облуживания заявок низшего приоритета (рис. 3). В начале алгоритма также обнуляется время освобождения канала обслуживания и число обслуженных заявок низшего приоритета. В цикле время начала облуживания Tn приравнивается ко времени поступления заявки низшего приоритета и проверяется условие, что канал свободен. Если занят, то заявка начнет об- служиваться в момент освобождения канала TOK.

На следующем шаге рассчитывается время окончания обслуживания данной заявки Tk2.

Теперь перебираем в цикле заявки высшего приоритета и проверяем, не помешают ли они обслуживанию данной заявки с низшим приоритетом. Последовательно проверяются ситуации 1 и 2. Если требуется, то пересчитываются времена начала и окончания обслуживания Tn и Tk2.

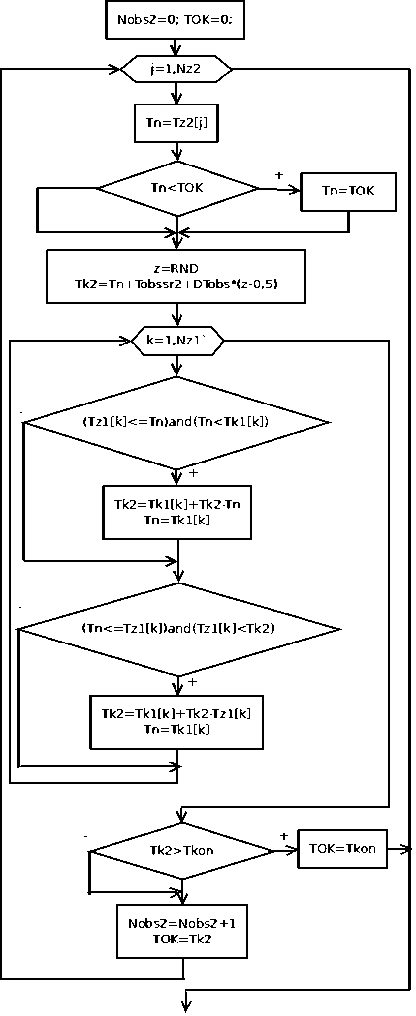
Рис. 3. Процедура обслуживания заявок низшего приоритета

После окончательного расчета Tk2 проверяем, не закончилось ли время функционирования системы. Если закончилось, то выходим из процедуры, иначе увеличиваем счётчик числа обслуженных заявок низшего приоритета на 1 и пересчитываем время освобождения канала.

Результаты. Разработанный алгоритм реализован в среде Delphi 7. Проведены расчёты с комбинацией переменных и параметров, предложенные в [1].

При сравнении разработанного алгоритма с описанным в работе [1] выделяются преимущества моего алгоритма:

• •    лучшая наглядность и более лёгкая сопровождаемость кода в связи с отсутствием операторов безусловного перехода;

• •    меньшая длина кода (например, процедура обслуживания заявок низшего приоритета написана в 36 операторах против 69 из [1]) при одинаковой сложности алгоритма.

Разработанный алгоритм используется при работе со студентами факультета Прикладной информатики Пермской ГСХА.

При изучении темы "Имитационное моделирование" на лабораторных работах студентам предлагается реализовать алгоритм в выбранной ими среде программирования.

Выводы

Алгоритмическое моделирование СМО может быть успешно использовано для отработки у студентов различных специальностей навыков написания прикладных программ. А также выработки навыков решения задач моделирования типовых экономических процессов, которые необходимы для успешной экономической и управленческой деятельности.