Модель стационарного неизотермического течения магмы в канале вулкана с учетом скольжения на границе

Проблема моделирования течения магмы в канале вулкана рассматривалась в ряде работ, ссылки на которые можно найти в [1–9]. В основном современные модели рассматривают подъем магмы как квази-одномерный, изотермический процесс ее движения по каналу цилиндрического формы с учетом прилипания к стенкам канала. Основной акцент делается на изменение при подъеме осредненных по поперечному сечению свойств магмы (содержания пузырьков и кристаллов). Так, в [3] исследуется влияние вязкой диссипации на динамику извержения. Задача решается в квази-двумерной постановке в приближении длинного канала. Показано, что в пристеночной области образуется слой горячей маловязкой магмы. Профиль скорости при подъеме изменяется от параболического до близкого к плоскому с большим градиентом около стенок канала. Появившиеся в последние годы экспериментальные данные по реологии магмы с большой концентрацией кристаллов [6, 8] до настоящего времени при моделировании течения магмы в канале вулкана не были учтены в полной мере.

В настоящей работе предложена модель неизотермического течения магмы в осесимметричном канале вулкана. В модели принято, что вязкость магмы зависит от температуры, скорости деформации и концентрации растворенного газа, являющейся функцией давления. Предусмотрена также возможность скольжения магмы по стенкам канала в соответствии с экспериментально определяемым законом [6].

Стационарное неизотермическое течение несжимаемой магмы в осесимметричном канале вулкана описывается системой дифференциальных уравнений в частных производных, отражающих законы сохранения импульса, массы и энергии. Математическая модель строится для экструзивного типа извержения, при котором истечение высоковязкой лавы из жерла вулкана считается медленным. Число Рейнольдса для такого течения мало, поэтому инерционными членами в уравнениях движения можно пренебречь.

Vp = VK cd (p), T, I 2) DJ + pg,

(v-v ) = 0,(2)

pCp (v - V)T = V - (XVT) + ц(Cd (p),T,12)D : D.(3)

Здесь: p — давление, T — температура, ρ — плотность, μ — эффективная вязкость,, v — вектор скорости потока магмы; cd — концентрация растворенного в магме газа; Cp и λ — коэффициенты теплоемкости и теплопроводности; g — вектор ускорения силы тяжести; D = V (vT + v) — тензор скорости деформации. На входе в канал (в очаге вулкана) задано давление pin и температура T0 . На стенках канала считается известной и постоянной температура Tw , а скорости удовлетворяют условиям прилипания или скольжения. Верхний индекс «Т» означает операцию транспонирования, символ « : » — свертку тензоров.

На основании экспериментальных данных [3, 6, 7] реологические свойства среды, зависящие от концентрации растворенного газа cd (p), температуры и второго инварианта 12 тензора скорости деформации, задаются уравнением ц(cd (p),T,12) = p0exp(A(cd,T))F(12). При этом функция температуры

и массовой концентрации растворенного газа A (cd, T) и функция второго инварианта тензора скорости деформации

A ( c d , T ) =- 3,545 + 0,833 L_c

9601 - 2368 L

+           c—

T - 195,7 - 32,25 L c

F ( I ₂ )       описываются выражениями [6]:

По        т,, I I 11

F ( I ₂) = ⁰ +--⁰  1 - exp - 2    , в которых обозначено:

Ц 0 Ц 0 1 2 I     А 1 2 Л

^Lc = ^{2 +} lg⁽ c d )  при   c d = c d 0 V p , если   c d 0 V p <  c dm  и   c d = c dm , если   c d 0 V p ^ c dm , где   c d 0 = ^Cf 4p ,

C_f — коэффициент растворимости газа; индексы означают: m — максимально возможную концентрацию газа, 0 — концентрацию, соответствующую давлению, создаваемому весом находящейся в канале неподвижной магмы p ₀ ; ц ₀ — вязкость при давлении p ₀ и температуре T ₀ ; р ₀ , т ₀ , I * — параметры нелинейности реологического уравнения.

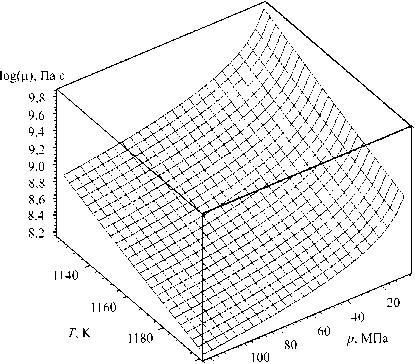
Следует отметить, что вязкость магмы плавно убывает с ростом температуры и резко увеличивается при снижении давления за счет уменьшения содержания растворенного в магме газа (Рис. 1, а ). В одномерном случае, при п ₀ = 0,5Па - с , т ₀ = 10 1 5 а , 1 2 = 2 - 10 - ^{5 1}, 1 ₂ = 5 v z /8r = Y ,с ростом скорости деформации в диапазоне 10 ^{- 5} < Y <  10 ^{- 3} эффективная вязкость снижается в пять раз, а вне этого диапазона остается практически постоянной (Рис. 1, б ). Решение задачи течения среды с такими нелинейными реологическими свойствами связано со значительными математическими трудностями, поэтому для ее реализации часто прибегают к численным методам.

Для общности постановки обезразмерим уравнения (1)-(3). В качестве характерных масштабов длины, скорости, давления, температуры и вязкости возьмем размерные величины: радиус канала вулкана R , типичную скорость экструзивного извержения v0 и характеристики течения магмы на входе в канал p0, T0, ц0. Тогда уравнения (1)-(3) примут вид:

а

1200    120

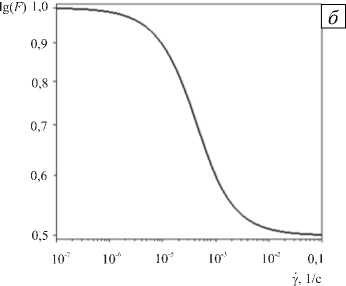
Рис. 1. Реологические свойства магмы: зависимость вязкости от температуры и давления в полулогарифмических координатах ( а ); зависимость F (Y) в одномерном случае ( б )

Vp' = a(V-[p' V( v'T + v ')J)-Kez,(4)

(V-v ') = 0,(5)

(v'-V)T' = vV-(VT') + РФ .(6)

Здесь Ф = ц ' ( C d ( p ), T , 1 2 ) [v ( v '^T + v ' ) : V ( v '^T + v ' ) ] ,

Ц P v 2 = 2 в = Ц о ^v 2 = 1 ^v 0 p v ₀ Rp о Re - Eu , ^P p v o R C p T Re C p T o ,

X      1        p v 2 gR 2

v=-------= —, k = —-— =----- -г где Re, Eu, Pe, Fr — соответственно, числа Рейнольдса,

P Cp V o R ^pe        p о v₀   Eu - Fr

Эйлера, Пекле и Фруда.

3.    Алгоритм численного решения

Согласно процедуре Галеркина, краевая задача (4)–(6) преобразуется в полуслабую вариационную форму с естественными граничными условиями для напряжений:

j { - ( V- u ) p ' +aV u : V

V

( v '^T + v ' ) } dV = -k J u - e z dV + p ' in j ue z dS ,

VS

J h ( V- v ') dV = 0,

V

J{V(v'- V)T'+ vW -VT'}dV = pj УФdV ,

VV где u,ΨH , — взвешивающие функции, p 'in — давление в очаге вулкана. В дальнейшем штрихи у безразмерных величин опускаются.

Решение полученной нелинейной системы (7) сводится к последовательности линеаризованных задач, в которых нелинейные члены рассчитываются по результатам предыдущих итераций. Сначала решается задача течения с постоянной вязкостью. Затем, с учетом найденных на предыдущей итерации компонент вектора скорости, решается задача конвективного теплопереноса. Далее по найденному температурному полю корректируется эффективная вязкость, а по полю скоростей вычисляются конвективные члены в температурной задаче. Процесс повторяется до достижения заданной точности.

На каждой итерации дискретизация линеаризованных задач осуществляется треугольными конечными элементами с линейной аппроксимацией компонент вектора скорости и температуры, а давление принимается кусочно-постоянным в пределах четырехугольников, состоящих из двух треугольных элементов. Сходимость итерационного процесса контролируется по эффективной вязкости ц , зависящей от основных параметров задачи — давления, температуры, скорости деформации. Предварительное исследование показало, что при низких перепадах давления ( p in <  1,1) итерационный процесс сходится менее чем за 50 шагов при относительной погрешности е = ц ^К / ц ^К 7 1 = 0,001. При возрастании перепада давления сходимость ухудшается, и после некоторого предельного значения p in >  1,6 процесс расходится, что связано с приближением к точке бифуркации решения [1–4]. Граничные условия первого рода для скорости и температуры удовлетворяются непосредственно присвоением соответствующим переменным заданных значений в граничных узлах.

Для того чтобы учесть проскальзывание по границе, обычно вводится итерационная процедура: задается начальное распределение v w , определяются из решения задачи т w на стенке, а затем по закону трения v w = f ( т w ), который обычно определяется экспериментально, вычисляется новое распределение v w . Однако при решении задачи методом конечных элементов можно обойтись без дополнительных итераций. Для этого расширим область решения, добавив один слой элементов с малой толщиной 5 к той части границы, на которой происходит проскальзывание. В узловых точках, находящихся на внешней границе расширенной области, зададим условия прилипания, а в узловых точках, лежащих на границе реальной области, потребуем выполнения условия непроникания основного материала в приграничный слой. Иначе говоря, будем считать, что в этом слое узлов нормальная составляющая скорости v _К принимает нулевые значения, а касательная v _T остается неизвестной и подлежит определению. В такой постановке в тонком фиктивном слое жидкости реализуется чистое течение Куэтта, в котором ц = f ( т w )/у , у = d v _T /д к = v w /5 .

Таким образом, расчет поля скоростей осуществляется по уравнениям одного типа, как для внутренних элементов, так и для фиктивного приграничного слоя. Отличие заключается лишь в реологических свойствах материалов фиктивного слоя и основной области, что легко учитывается в методе конечных элементов. В результате закон трения на границе удовлетворяется автоматически.

4. Результаты численного моделирования

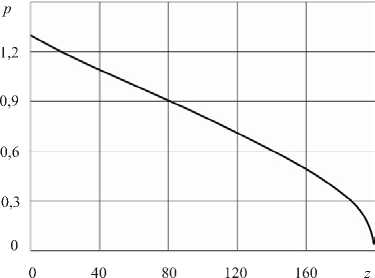
Рис. 2. Распределение безразмерного давления по длине канала при давлении на входе p in = 1,3

Исследовалось течение магмы в канале вулкана при различных значениях давления на входе, реологических свойствах магмы и условиях на границе канала. Задача решалась в цилиндрической системе координат с началом в очаге вулкана и осью z, которая совпадает с осью канала. Как пример расчета представлены профили давления, скорости и температуры в канале вулкана при безразмерном давлении pin = p/p0 = 1,3. Выбор такой величины давления обусловлен, с одной стороны, возможностью наглядной демонстрации основных физических процессов, имеющих место при истечении магмы (заметного влияния диссипации, нелинейной реологии и скольжения на стенке), а с другой стороны тем, что величина давления не превышает точки бифуркации, после которой происходит неконтролируемое возрастание расхода    магмы.    Другие    характерные параметры задачи:    R = 25 м; L = 5000 м;

p ₀ = р gL + p_a = 1,226 - 10 8 Па;     p a = 2,5-10⁶ Па;     v ₀ = 1 м/с;     T 0 = 1123K;     C p = 1200Дж/(кг - K);

ц0 = 3,7-1Па с - ; Cf = 4,11-10Й а) 1/2; р = 2500 кг/м3; cdm = 0,05. Им соответствуют безразмерные координаты r' = r/R, z' = z/R (далее штрихи опускаются) и критерии: Re = 1,69; Eu = 4,9 -104; Pe = 3,7 -107; Fr = 6,4 -10-2; к = 5 -10—3; v2 Д Cp ■ T0 ) = 7,4 -10-7. В качестве закона трения было принято условие постоянства безразмерного касательного напряжения на границе канала тw = 100 , которое можно интерпретировать как предел прочности материала на сдвиг.

Расчеты показывают, что давление слабо меняются по радиусу канала, а его изменение по длине представлено на рисунке 2. Профили продольной скорости и температуры существенно меняются от входного сечения к выходному (Рис. 3). Радиальная компонента скорости не превышает 0,1% от продольной, поэтому не приводится.

В окрестности входа в канал вулкана давление велико, а вязкость магмы относительно низкая, поэтому вязкая диссипация не приводит к значительному росту температуры. При подъеме магмы, сопровождающемся падением давления, ее вязкость возрастает. Вследствие этого в пристеночной области существенно увеличивается температура и происходит выполаживание профиля скорости в центральной части канала, а вблизи стенки профиль становится круче. Возрастание градиента скорости совместно с ростом вязкости за счет падения давления в пристеночной области ведет к увеличению по модулю касательного напряжения на стенке т = цд у z /д r , которое может превысить критическое значение т w . В этом случае на части граничной поверхности начинается проскальзывание магмы по стенке канала (Рис. 4). С другой стороны, с ростом давления в очаге вулкана касательные напряжения на стенках канала в зоне прилипания увеличиваются (по модулю), а в зоне скольжения остаются постоянными. При этом зона скольжения расширяется, и расход магмы Q резко возрастает (Рис. 5). В пределе, когда

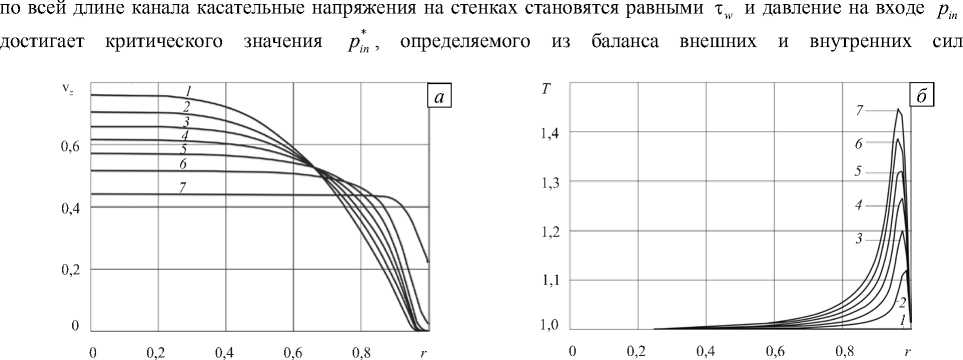
Рис. 3. Безразмерные характеристики неизотермического неньютоновского течения в условиях частичного проскальзывания при давлении на входе p n = 1,3 : профили продольной скорости ( а ) и температуры ( б ); цифрами обозначены номера поперечных сечений канала от входного ( 1 ) до выходного ( 7 ) через равные промежутки по длине

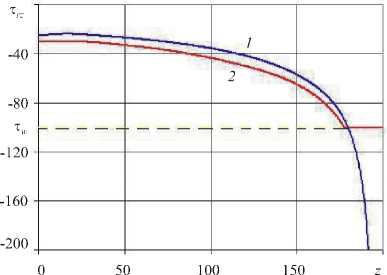
Рис. 4. Распределение касательного напряжения на стенке канала при давлении на входе p n = 1,3 в случае изотермического течения с прилипанием ( 1 ) и частичным проскальзыванием на стенках канала ( 2 )

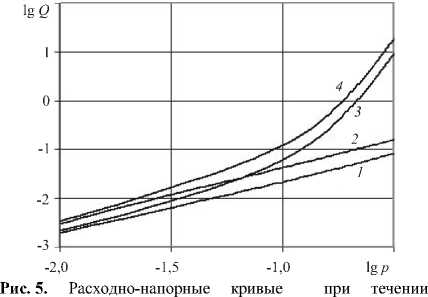
неньютоновской магмы при давлении на входе p n = 1,3: изотермическое ( 1 ) и неизотермическое ( 2 ) течения прилипанием; изотермическое ( 3 ) и неизотермическое ( 4 ) течения с проскальзыванием

RL

2 л | ( ( p n ( r ,0 ) - p ₀ )/ p ₀ ) rdr =п | т _rz ( R , z ) dz , наступает неконтролируемое возрастание расхода. Это один 00

из возможных механизмов перехода от течения экструзивного типа к взрывному извержению. Расчеты показывают, что учет проскальзывания магмы вдоль стенок канала вулкана приводит к гораздо более существенному росту расхода магмы, чем учет вязкой диссипации. Ранее этот факт в моделях не учитывался.

5. Заключение

Построена двумерная осесимметричная модель стационарного неизотермического течения нелинейновязкой несжимаемой магмы в цилиндрическом канале вулкана. Разработаны алгоритм и вычислительная программа, базирующаяся на методе конечных элементов.

Показано, что распределение давления и концентрации растворенного газа для несжимаемой магмы представляет собой нелинейно убывающую по длине канала функцию, слабо зависящую от радиуса. Сдвиговая деформация, диссипация механической энергии, максимум температуры и минимум эффективной вязкости локализуются вблизи стенок канала с ростом максимальных значений в направлении выходного сечения. Проскальзывание магмы снижает локализацию сдвига у стенок и ведет к снижению диссипации энергии и уменьшению разогрева магмы в приграничной области. С другой стороны, превышение критического значения давления p_i ^* _n в очаге вулкана приводит к тому, что зона проскальзывания занимает всю область канала вулкана и происходит неконтролируемое возрастание расхода. Это один из возможных механизмов перехода от экструзивного режима к взрывному извержению.