Модель стохастического съема припуска и формирования поверхности при плоском шлифовании периферией круга для автоматизированного управления процессом

металла от микрорезов по временным интервалам позволяет определить, например, срезаемый объем металла в 1 секунду.2

Таким образом, стоит задача разработки модели стохастического съема припуска и формирования поверхности при плоском шлифовании периферией круга. Для этого форму зерна аппроксимируем некоторой фигурой, которая движется по круговой траектории (зерно расположено на круге значительно большего диаметра, чем размер самого зерна), врезается в деталь и срезает материал, оставляя микроцарапину в виде сектора тора. Готовая поверхность детали образуется в результате наложения множества таких микроцарапин друг

на друга. Разработка модели стохастического съема припуска проводилась в несколько этапов:

• 1.    Моделирование формы абразивного зерна.

• 2.    Моделирование формы микроцарапины (риски).

• 3.    Продольное наложение рисок.

• 4.    Поперечное наложение рисок.

• 5.    Стохастическое наложение рисок.

1.    Моделирование формы абразивного зерна

Существуют различные подходы к аппроксимации формы абразивного зерна: шар, параболоид вращения, усеченная пирамида, усеченный конус и др. Максимальное приближение аппроксимируемой фигуры к реальному профилю обеспечивается при использовании параболоида вращения. Однако математическое описание параболоида сложнее, чем описание шара, поэтому для нашей задачи, в которой предполагается формирование шлифованной поверхности от воздействия нескольких десятков тысяч абразивных зерен, мы выбираем аппроксимацию шаром.

В состав каждого шлифовального круга входят 40–45 % зерен основной фракции, а 55–60 % зерен имеют соответствующие отклонения по ГОСТ Р52381-2005 [2]. Поэтому диаметр b (рис. 1) абразивных зерен имеет нормальное распределение N(b, μ, σ) [3]:

,        -( b - ц)²

N ( b ,ц,о) - -^=e ²⁰   .                (1)

• σ 2π

  

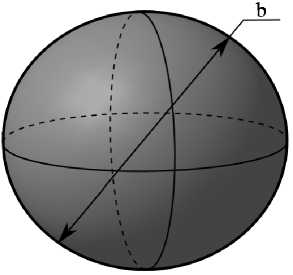
  Рис. 1. Модель абразивного зерна

  
  
  

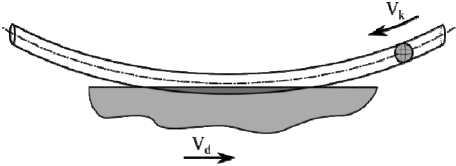
  Рис. 2. Схема образования риски при плоском шлифовании периферией круга

  
  

Поскольку скорость вращения круга в десятки раз выше скорости движения детали, т о за время п р охождения зерном через дугу контакта деталь совершит столь незначите л ьное перемещение, что и м можно пренебречь. Очевидно, что д лина риски будет равна длине дуги контакта, спроецированн о й на плоскость детали. П ри плоском шлифован и и длина дуги контакта рассчитывается по формуле (2) и может принимать значения от 1 до 10 мм и более.

L k - 2 №, (2) где D – диаметр шлифовального круга; t – глубина врезания.

Расчет формы едини ч ной риски п роисходит следующим образом (рис. 3). По дли н е риски с н е которым интервалом (0,01–0,1 мм в зависимости о т степени точности расчета) делаю т ся сечения п о перек. Таким образом, получаем множество п о чти плоских задач. Затем в каждом таком сечен и и решается задача – нахождение гл у бины проф и ля впадины. Для этого профиль разбивается на и н тервалы y 1 , y 2 , y 3 , …, y i ч ерез 0,01–0,1 мм и для каждого интервала находится глубин а профиля. Через уравнение окружности ( У - У o ) 2 + ( z - z o ) 2 - R ² м о жно опред е лить высоту точек профиля, прина д лежащих окружности: z ^- z 0 ± V ^{R 2 - (} У ^- y 0^{) 2} .

Для нашей задачи: y - yk (k -1,2,3, ..., i), z - zi,

Db

У о ^- 0, z о ^- у + 2 ^- t ,

Db

R - —F — . Таким

о б разом, формула расчета высоты каждого интерва л а профиля:

z k ^-

Db

+ — t k = 1, 2, 3, …, i.

Db

--1--

^^^^^^B

y_k 2

3.    Продольное наложение рисок

Как было сказано выше, скорост ь вращения к р уга в десятки раз выше, чем продольное перемещение стола. Поэтому, как правило, за один рабочий ход стола с деталью круг успевает сделать н е сколько оборотов, в результате чег о возникает п е риодичность наложения рисок и, следовательно, рельефа обработанной поверхности. Т аким образом, каждое зерно оставляет несколько рисок, которые располагаются друг з а другом на некотором

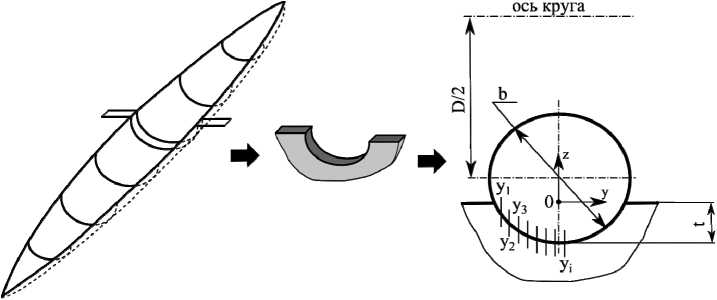
Рис. 3. Расчетная схема определения профиля риски

расстоянии. Для определения величины этого расстояния, а также влияния различных входных параметров процесса на наложение рисок рассматривается единичное сечение детали и круга, на котором расположено единичное зерно (рис. 4).

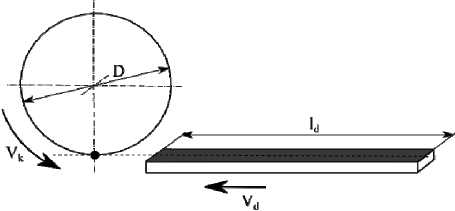
Рис. 4. Расчетная схема

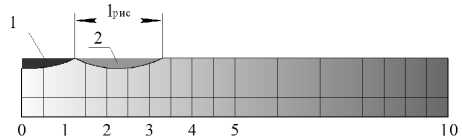
Профиль детали длиной ld движется со скоростью Vд влево, шлифовальный круг диаметром D вращается со скоростью Vк. На круге расположено одно зерно. За рабочий ход стола зерно вступает в контакт с деталью с периодом, равным времени одного оборота шлифовального круга. Введем понятие «периодичность расположения рисок» – LT – это величина, равная расстоянию между началом предыдущей и началом последующей рисок, образовавшихся от микрорезания единичным абразивным зерном (рис. 5). Периодичность расположения рисок – есть величина поступательного перемещения детали за время одного оборота круга:

L _ ^ D • V д T 60 • V

.

Для различных скоростей движения рабочих органов периодичность расположения рисок, рассчитанная по (4), существенно различается, определяя схему снятия всего припуска. Нами выделе- но четыре возможных варианта периодичности расположения рисок от единичного абразивного зерна:

• 1.    0 < L T < l min . Деталь за полный оборот круга перемещается на расстояние, которое меньше миним а льной толщины среза. В таком слу ч ае зерно не режет материал детали, а трется задней поверхностью о деталь, вызывая упругие деформации (рис. 6, а).

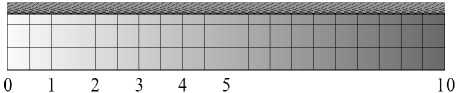
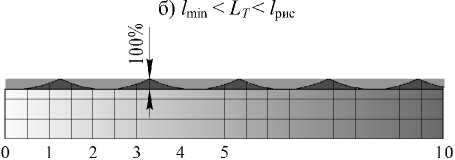
• 2 .    l min < L T < l рис . Деталь за один обо р от круга перемещается на расстояние, которое меньше, чем длина риски, но больше, чем толщина минимального среза. В этом случае зерно на каждо м обороте кру г а срезает слой металла, причем каж д ая последующая риска перекрывает предыдущую. Такая схе м а съема припуска похожа на фрезерование, когда каждый зуб фрезы снимает слой металла (рис. 6, б).

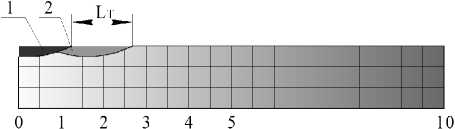
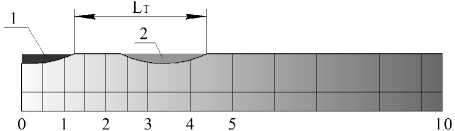
• 3.    L_T = l _рис . Деталь за один оборот к р уга переме щ ается на расстояние, равное длине риски. В этом случае риски выстраиваются друг за другом, перекрытия рисок и необ р аботанный материал отсутствуют (рис. 6, в).

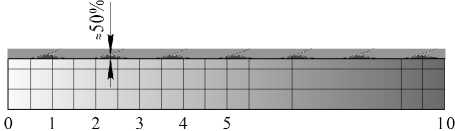
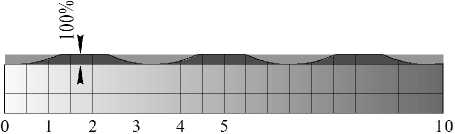
• 4.    L T > l рис . За один оборот круга деталь переме щ ается на расстояние, которое больше длины риски. В таком случае от с утствует перекрытие рисок и остаются участки н е обработанного материала (рис. 6, г).

Для каждого варианта периодичности расположения рисок рассмотрим полный рабочий ход стола, т. е. не два, а множе с тво оборото в шлифовального круга с единичным абразивным зерном.

• 1.    0 < L T < l min . Резание при таких небольших перемещениях не соверша е тся, но рассмотрим формирование поверхности подробнее: на первом обороте круга толщина срезаемого зерном слоя

  

  Рис. 5. Периодичность расположения рисок

  
  

• 2.    l min < L T < l _рис . Высота оставленных гребешков может принимать различные значения: минимальное (до 5 % от t ) – при приближении к первой схеме съема припуска и максимальное (до 95 % от t ) – при приближении к третьей схеме съема припуска (рис. 7, б).

• 3.    L T = l _рис . Риски располагаются точно друг за другом (рис. 7, в).

• 4.    L T > l _рис . Единичное зерно снимает не весь п р ипуск, между рисками располагаются участки н е обработанного материала. Размер детали не изменяется (рис. 7, г).

меньше минимальной толщины среза, поэтому резание не происходит. На втором обороте круга припуск увеличивается в два раза, и если толщина среза меньше минимальной толщины среза, то резание не происходит. Но в какой-то момент накопленный на предыдущих оборотах припуск превысит значение минимальной толщины среза и зерно срежет слой материала. Таким образом, при первой схеме периодичности расположения рисок резание будет производиться через несколько оборотов круга (рис. 7, а).

Прилегающая плоскость (линия) к рельефу сечения после резания единичным зерном

Введем понятие прилегающей к обработанной поверхности плоскости – это плоскость, геометрически проходящая через верхушки несрез а нного матер и ала (рис. 8). Обозначим высоту расположения прилегающей к выступам плоскости относительно идеальной обработанной поверхностью как h пп .

Рассмотрим один период, т. е. генерирование рисок от первого и второго оборота круга. Рас-

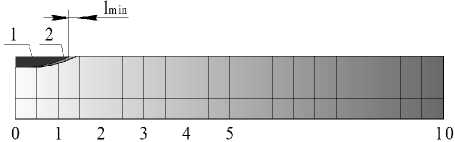
а) 0 <  L_T <  l _min

а) 0 <  L_T <  l _min

б) l _m i _n<  L_T <  l _рис

в) L_T = l _рис

в) L_T = l _рис

• г) L_T = l _рис

Рис. 6. Наложение рисок при различных величинах периодичности

• г) L_T >  l _рис

Рис. 7. Формирование поверхности за рабочий ход стола с заготовкой при различных значениях периодичности наложения рисок

Прилегающая к вершинам выступов плоскость

Рис. 8. Вершины выступов после обработки и прилегающая к ним линия

стояние между центрами рисок равно величине периодичности наложения рисок, рассчитанной по (4). Верхушка необработанного материала располагается ровно посередине между первой и второй риской, поэтому введем систему координат x 0 z так, чтобы вертикальная ось 0 z проходила через верхушку, а горизонтальная ось 0 x находилась на идеальной обработанной поверхности (рис. 9).

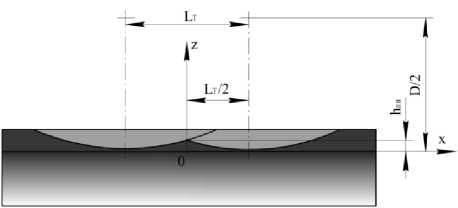
Рис. 9. Схема расчета высоты оставшихся выступов

Необходимо определить высоту прилегающей к выступам плоскости, или, как следует из рисунка, координаты точки, расположенной на траектории кругового движения зерна через материал заготовки. Из формулы определения окружности ( x - x 0 ) 2 + ( z - z 0 ) 2 = R ² можно определить координату любой точки, принадлежащей окружности: z = z ₀ ± ^R ² - ( x - x ₀)² . Для нашей задачи: x = 0,

L DD z = hпп, x0 = -^-, z0 = —, R = —. Таким образом, hпп

D

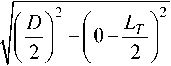
После преобразо-

ваний получим формулу для определения высоты расположения прилегающей к вершинам выступов плоскости относительно идеальной обработанной поверхности:

h

пп

D - л]D ² - L_T²

Параметром, предопределяющим высоту неровностей при конкретной технологической ситуации (когда диаметр круга не может быть изменен), является периодичность расположения рисок, которая в свою очередь является функцией L t = f ( V _K, V_A , D ).

Рассмотрим влияние периодичности расположения рисок L T на высоту прилегающей плоскости. Как было показано ранее, существуют три различных варианта периодичности расположения рисок L T , для каждого из которых схема съема всего припуска различна.

• 1.    0 <  L_T <  l min . Круг вращается со скоростью,

• 2.    l _min <  L_T <  l _рис. В данном случае образуются неровности, высота прилегающей плоскости к которым варьируется от t min до t . При приближении L T к l min высота прилега ю щей плоскости приближается к t min , а при приближении к l рис – стремит с я к t .

• 3.    L_T >  l _рис. В данном случае расчетная величина h пп принимает значени я , равные или превышающие величину припуска на обработку t . h „ = t пп max     ^.

которая гораздо выше скорости движения заготовки, высота прилегающей плоскости стремится к нулю hпп ^ 0, т. е. припуск на обработку полностью снят и шлифованная поверхность является идеальной плоскостью. Такая ситуация идеальна, но в реальности невозможна, поскольку всегда присутствует минимально необходимая толщина резания (tmin), меньше которой резание не будет осуществляться. Поэтому минимально возможное значение высоты расположения прилегающей плоскости равно tmln. hпп min = tmin .

Рассмотрим примеры для каждого случая. Исходные данные, которые будут постоян н ыми для каждого случая: диаметр шлифовального круга ( D ) – 250 мм, глубина резания ( t ) – 0,1 мм.

• 1.    V к = 80 м/с, V д = 10 м/мин. Длина каждой риски ( l _рис) при таких режимах резания будет равна 10 мм, а периодичность н а ложения рисок ( L_T ) – 1,63 мм. Тогда по зависимости 1 высота несрезан-ных верхушек h пп = 0,003 мм. Проведен компьютерный эксперимент с этими же исходными данными в разработанной трехмерной моде л и формирования шлифованной поверхности. По результатам моделирования (рис. 10, а) при резании с таким и скоростями на дне канала, образованного рисками, остаются гребешки высотой 0,002 мм.

• 2.    V к = 50 м/с, V д = 20 м/мин. Длина каждой риски ( l рис ) при таких режимах резания будет равна 10 мм, а периодичность н а ложения рисок ( L_T ) – 5,23 мм. Тогда по зависимости 1 высота несрезан-ных верхушек h _пп = 0,027 м м . Моделиро в ание показало (рис. 10, б), что высота остающ и хся гребеш к ов h пп = 0,025 мм.

• 3.    V к = 35 м/с, V д = 26,5 м/мин. Длина каждой риски ( l рис ) при таких режимах резания будет равна 10 мм, а периодичность н а ложения рисок ( L T ) – 10 м м. Тогда по зависимости 1 высота несрезан-ных верхушек h пп = 0,098 м м . Моделиро в ание показало (рис. 10, в), что высота остающихся гребеш к ов h _пп = 0,097 мм.

Построим график зависимости высо т ы расположения примыкающей плоскости ( h _пп) о т периодичности наложения рисок для каждого диаметра шлифовального круга: 200 , 250, 300, 400 мм (рис. 11). Как было сказано ранее, мак с имальная высота расположения плос к ости не может быть больше величины снимаемого припуска ( t ). Максимальная величина припу с ка на один рабочий ход при плоском шлифовании в общемашиностроительных нормативах режимов резания равна 0,5 мм. Поэтому графики зависимостей о граничены 0,5 мм по координате h _пп. Минимальная же высота расположения плоск о сти приним а ется t _min,

в)

Рис. 10. Схема расчета высоты оставшихся выступов

значение которой зависит от зернистости шлифо- вального круга.

Выход на время обработки за один рабочий ход (tобр) для определения самого быстрого съема lд сделаем через скорость движения детали: V = -д- , д р.х где lд – длина детали. Подставим Vд в уравнение периодичности наложения рисок (4) и оттуда выйдем на зависимость tр.х(LT):

^t р.х.

”• D • ¹ д

60 • V • L_T ' к T

Время одного рабочего хода (6) прямо пропорционально длине детали l д . Для построения графика зависимости t р.х ( L T ) удобно взять значение l д такое, чтобы значение L T было от 0 до 0,5. Построим график зависимости (6) для следующих входных технологических параметров: D = 250 мм, l д = 5 мм (рис. 12). Пересечения графиков на рис. 12 – это технологические ситуации, при которых будет обеспечиваться минимальная высота расположения прилегающей к вершинам выступов h пп при минимальном значении времени рабочего хода стола. Если взять L T такое, чтобы сократить время рабочего хода, то высота прилегающей плоскости увеличивается, соответственно, увеличивается и шероховатость, снижается интенсивность съема металла. Если же взять L T такое, чтобы высота прилегающей к выступам плоскости стремилась к нулю, то время на обработку существенно повысится.

Периодичность наложения рисок зависит от скорости перемещения детали для каждой скорости круга. В общемашиностроительных режимах резания максимальное значение скорости движения стола 32 м/мин.

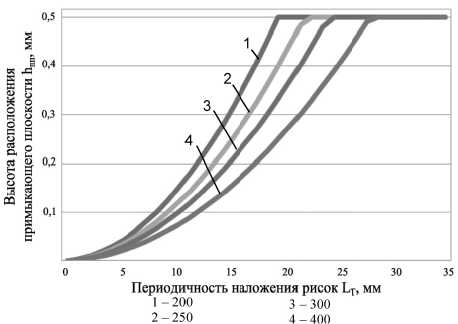
Рис. 11. Зависимость высоты расположения примыкающей плоскости ( h пп ) от периодичности наложения рисок

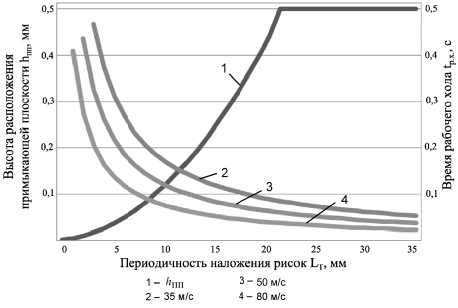
Рис. 12. Зависимость высоты расположения примыкающей плоскости ( h пп ) от периодичности наложения рисок для различных скоростей вращения круга

4.    Поперечное наложение рисок

Предположим, что соотношение V к и V _д такое, что наложение рисок не происходит, тогда для всего съема припуска одного зерна в каждом сечении недостаточно. Тогда несрезанные выступы (3 и 4 схемы) должны срезаться либо зерном, находящимся в этом же сечении на некотором расстоянии от первого зерна, либо зерном, расположенным в соседнем сечении. При такой схеме снятия припуска осуществляется поперечное наложение рисок от случайно расположенных зерен, т. е. осуществляется стохастическое резание.

При нахождении профиля конкретной риски производятся вычисления глубин участков риски по формуле (3), после расчета сравниваются значения глубины риски и высоты профиля детали. Если координата глубины риски ниже профиля детали, то значение высоты профиля на данном участке принимается равным глубине риски. Если же глубина риски выше профиля детали (т. е. зерно не задело металл), то высота профиля детали остается прежней. Такая проверка на наличие металла под зерном в рассчитываемой точке осуществляется логическим предикатом сравнения величин. На рис. 13 приведены результаты расчетов в модели-программе с предикатом сравнения глубины риски и высоты профиля. На рис. 13, а абразивное зерно снимает металл с еще необработанной, плоской поверхности. По алгоритму расче- та профиля риски находятся глубины участков риски, и формируется новая поверхность в виде сектора тора. На рис. 13, б происходит аналогичное действие для второго зерна, меньшего размера. На рис. 13, в третье абразивное зерно попадает в перемычку металла между первой и второй рисками. Там, где металл есть, формируется новая поверхность, а там, где металл отсутствует, остается исходная поверхность детали. На рис. 13, г опять срезается необработанный слой металла, формируется целая риска. А на рис. 13, д зерно опять попадает в перемычку между рисками, срезая ее. Таким образов, мы наблюдаем формирование обрабатываемой поверхности в результате поперечного наложения рисок.

5.    Стохастическое наложение рисок

Разработан алгоритм, в котором совмещены модель формирования профиля единичной риски, продольного и поперечного наложения множества рисок. По алгоритму написана программа, результатом расчетов в которой является рельеф детали после обработки. При моделировании соблюдены основные особенности строения шлифовального кру г а: зерна имеют нормальное распределение их раз м еров, а координаты расположения центров зерен назначаются в програ м ме по равномерному закону распределения величин.

Модель формирования шлифованной поверх-

д) пять рисок

Рис. 13. Поперечное наложение шлифовальных рисок

Рис. 14. Поверхность, образованная стохастичным наложением 150 000 шлифовальных рисок друг на друга

ности позволяет рассмотреть формирование поверхности детали от любого количества абразивных зерен, с различной зернистостью и структурой круга, различными скоростями резания. На рис. 14 представлены результаты моделирования в имитационной модели стохастического съема припуска.