Модель связи упруго-вязкого смещения поверхности колеса относительно рельса с тяговыми характеристиками
Автор: Лапшин Виктор Петрович, Туркин Илья Андреевич, Носачв Сергей Викторович
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 5 (66) т.12, 2012 года.
Бесплатный доступ
Представлена модель учёта деформаций в узлах трения типа колесо — опора. Модель позволяет оценить влияние динамики тангенциальных деформаций в контакте колеса и рельса на динамику тяговых усилий, прилагаемых к центру масс колеса. Полученный математический аппарат описывает динамику системы в узле трения до момента срыва сцепления.
Силы трения, позиционирование, точность
Короткий адрес: https://sciup.org/14249878
IDR: 14249878 | УДК: 681.5.017+681.5.075
Текст научной статьи Модель связи упруго-вязкого смещения поверхности колеса относительно рельса с тяговыми характеристиками
Таким образом, проблема анализа эффекта проскальзывания и синтеза систем управления движения с учётом этого явления представляет собой актуальную научную задачу.
Длина площадки контакта. Площадка контакта колеса и рельса имеет эллиптическую форму [7]. При этом продольная ось площадки значительно длиннее поперечной. В дальнейшем будем использовать термин «длина площадки контакта», имея в виду длину продольной оси.
Эксплуатация автомобильной техники доказывает, что чем больше длина площадки контакта, тем лучше сцепление. С другой стороны, не требует доказательства тот факт, что чем больше деформация колеса под действием нормальной силы, тем больше длина площадки контакта. Введём переменную, характеризующую степень деформации колеса, и определим зависимость длины площадки контакта от этой переменной. Для наглядности рассмотрим деформационные изменения на рис. 1, где R — радиус колеса, хг — величина деформационных изменений колеса под действием нормальной силы, L — длина площадки контакта.
Используя простые геометрические рассуждения, определим зависимость длины площадки контакта от величины деформационных изменений колеса под действием нормальной силы:
Рис. 1. Влияние нормальной деформации колеса на длину площадки контакта
Эффект проскальзывания. На рис. 1 показано, что реальный радиус колеса при нормальной нагрузке меньше радиуса колеса, не имеющего вертикальной нагрузки, на величину х2- Во время движения колёсного транспорта всегда происходит обкатка колеса, то есть путь, пройденный центром масс колеса, будет меньше расчётного (с учётом недеформированного радиуса колеса). Связывая путь, пройденный колесом, с угловой мерой этого пути, можно получить две зависимости 5) = aR и Sz = a^R-x^, отличающиеся друг от друга только наличием или отсутствием деформации хг. Отметим при этом, что всегда будет справедливо неравенство 5) > Sz. Разницу между 5) и Sz в железнодорожной технике обозначают как «псевдоскольжение» [6]. Псевдоскольжение называется так потому, что присутствует даже в условиях чистого качения. Вместе с тем тангенциальная сила (сила тяги), приводящая к линейным перемещениям локомотива и подвижного состава, не зависит от псевдоскольжения, так как в условиях чистого качения сила тяги равна нулю. При описании движения железнодорожной техники зависимость силы тяги от проскальзывания представляют в виде нелинейной падающей характеристики [1,10,15].
Принято разделять действующую в зоне контакта тангенциальную силу, возникающую в условиях вращательного движения колеса, как совокупность следующих сил:
-
— сила трения сцепления (покоя) Ртр.сц:,
-
— сила трения скольжения FTp.CK :,
-
— сила трения качения FTp,K..
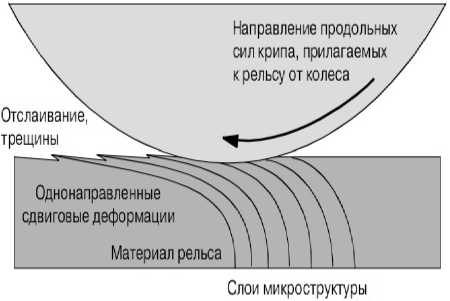
Величину проскальзывания (крипа) в железнодорожной технике принято обозначать Л [1]. Она определяется как разность угловой скорости колеса, приведённой к линейной через радиус колеса, и скорости линейного движения центра масс колеса [7]. В такой интерпретации одной из составляющих проскальзывания выступает и псевдоскольжение, но величина, характеризующая скорость псевдоскольжения, постоянна, а скорость проскальзывания — величина переменная, следовательно, псевдоскольжение не является крипом. Крип — это упруго-пластинчатые деформации в материалах рельса и колеса, результат которых — накопление продольных деформаций в материале рельса и колеса [7, 10]. Схематичное изображение таких деформаций и вид реально деформированного рельсового пути представлены на рис. 2 [7].

-
а) б)
Рис. 2. Пояснение к возникновению продольных деформаций в зоне контакта колеса и рельса (а), пример продольной деформации пути (б)
Продольные деформации в материале рельса вызваны тангенциальной составляющей силы, действующей со стороны колеса навстречу линейному движению центра масс колеса. Уравнение связи сил, действующих в контакте колеса и рельса на материал рельса, с учётом деформации колеса под действием нормальной нагрузки, можно записать в виде следующего уравнения:
(R — v \ (R — y \
М J d2kx
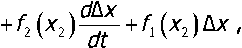
где Ах — переменная, характеризующая степень продольной деформации материала рельса; fi (х^ — функция, характеризующая упругие свойства материала рельса; f, (х^ — функция, характеризующая диссипативные свойства материала рельса; J — момент инерции колеса; М — внешний момент, приложенный к колесу.
В выражении (2) отсутствует инерционная составляющая сил сопротивления деформации рельса в связи с малостью массы, участвующей в этом движении.
Проскальзывание в условиях продольного движения центра масс колеса. Длина площадки контакта, как отмечалось выше, зависит от величины нормальных деформаций х2, но площадка контакта имеет помимо длины ещё и время существования, которое зависит от скорости продольного движения центра масс колеса — 14- Сила тяги, приводящая центр масс колеса в движение, связана с величиной продольных деформаций в материале рельса — позиционная составляющая сил в правой части выражения (2). Так как время существования площадки контакта ограничено, то также ограничено время формирования позиционной составляющей силы, противодействующей продольной деформации рельса. Исходя из этого, определим зависимость величины продольных деформаций от длины площадки контакта — L, скорости реального (с учётом проскальзывания) продольного движения центра масс колеса — 14 и скорости движения центра масс колеса без учёта проскальзывания — 1/а в следующем виде:
^ = \\_к^"^,
где а — угол поворота колеса,
“4/
Найдём интеграл (3):
где ха (t) = (R -х2)о — координата, характеризующая идеальное (без проскальзывания) про'
дольное движение центра масс, xi — координата, характеризующая реальное продольное движение центра масс колеса. В условиях стабилизации параметров движения, когда 14 и 1/а постоянны, значение проскальзывания можно определить как
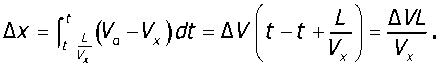
В выражении (2) помимо значения Ах присутствует также первая производная по времени от Их , которая может быть определена из выражения (3) следующим образом:
dt dt dt dt dt / dt =
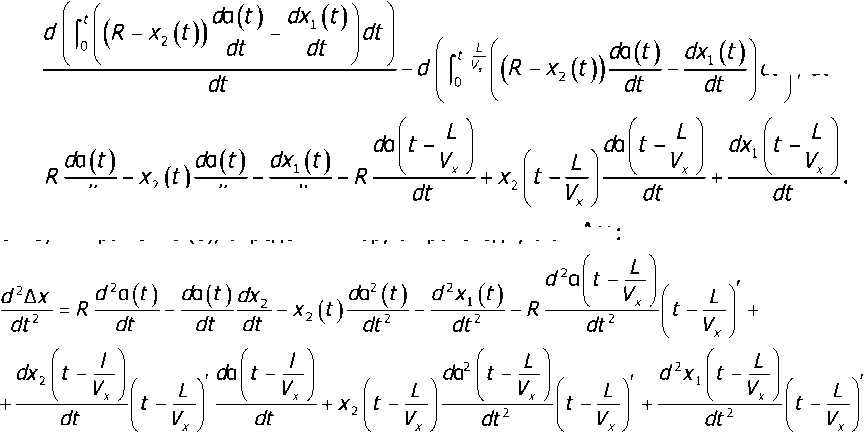
dt
dt dt
Используя выражение (8), определим вторую производную от Их:
где
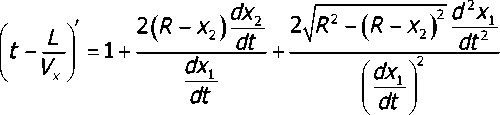
Модель взаимодействия сил с учётом проскальзывания. Для построения модели, описывающей движение системы колесо — рельс с учётом эффекта проскальзывания, определим оси координат и силы, действующие на систему.
С учётом существования площадки контакта передача тангенциального усилия связана с соотношением длины площадки контакта и величины проскальзывания. Рассмотрим передачу тангенциального усилия в условиях различных соотношений площадки контакта и величины проскальзывания.
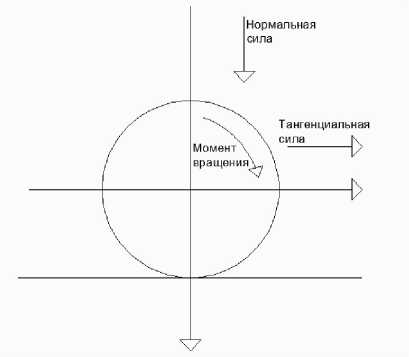
Рис. 3. Оси координат и силы, действующие в контакте колеса и рельса
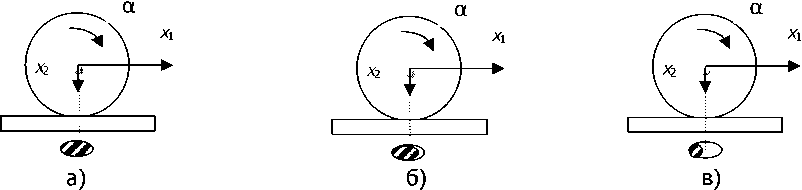
Рис. 4. Связь величины проскальзывания и длины площадки контакта: нет проскальзывания (а), величина проскальзывания не превосходит половины площадки контакта (б), величина проскальзывания больше половины длины площадки контакта (в)
В рассматриваемом на рис. 4, б случае величина проскальзывания не превосходит половины длины площадки контакта Дх < поэтому контакт можно свести к точечному представлению и модель, описывающая взаимодействие сил, будет выглядеть следующим образом [11—13]:
М
d7Lx
(D _ у \ (О _ У A
dhx dt
н^ у ti (х2)Дх-FrpK = т-^ + 1т
dxx
d^x P = m12^ + f dt2 22
da) dx. , dtW+f"
аэр- dt
(ob)
— х,, Adt 2
(Ю)
где P = mg — сила тяжести, действующая через колесо на площадку контакта, FTp.K . = кт.кР (/^.„«0,01 — для железнодорожного транспорта) — сила трения качения.
В случае, представленном на рис. 4, в, величина проскальзывания больше половины площадки контакта и сила, передаваемая на центр масс колеса, будет иметь не только тангенциальную, но и нормальную составляющую. Величину угла отклонения правой точки контакта от точки, определяемой нормалью, опущенной из центра масс колеса к поверхности рельса, можно приближённо определить как
‘“А
La~---^
R
Значение угла отклонения, при котором происходит срыв контакта, с учётом (1) будет приближённо равно
Да = мтах А '
V К
С учётом вышеизложенного, модель, представленная выражениями (10), примет вид
М
d2Hx
(D — у \ (D у А /УУ^
d^x , z ХЛ
—+ Гп(х2)Дх
/У 2 у f^t^x- cos (Да) - FTp к = m -^ + haap. ^
n d2x. , (do?\dx7 , (doA dt2 22 {dt) dt 21 {dt) 2
Упростим модель, представленную системой (13), предположив наличие линейной зависимости функций f12, fxx , f22, f21 от своих аргументов [14]:
М
d2Lx
(D — у \ (D _ у А /УУ 2
, dLx . .
+ кэхэ---+ к,хэДх
12 2 dt 11 2
, л \ с d2x. , dx,
(И)
kxxx7to • cos (Да) - FTp.K . = m -^ + ha3p -^
Р = m —+ k„ 1 + km — —- + k., 1 + k„., — x. dt2 22 1 “22 dt) dt 21 ( 0,21 dt J 2
Подставив (14) в выражения (6, 8, 9), получим модель, описывающую динамику контактного взаимодействия колеса и рельса с учётом эффекта проскальзывания 15:
^W) = /? W)^
dt2 dt dt
, 4cfc]2(Д) d2xx(tA
+ x7(t) —И +--
21 ’ dt2 dt2
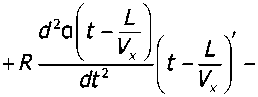
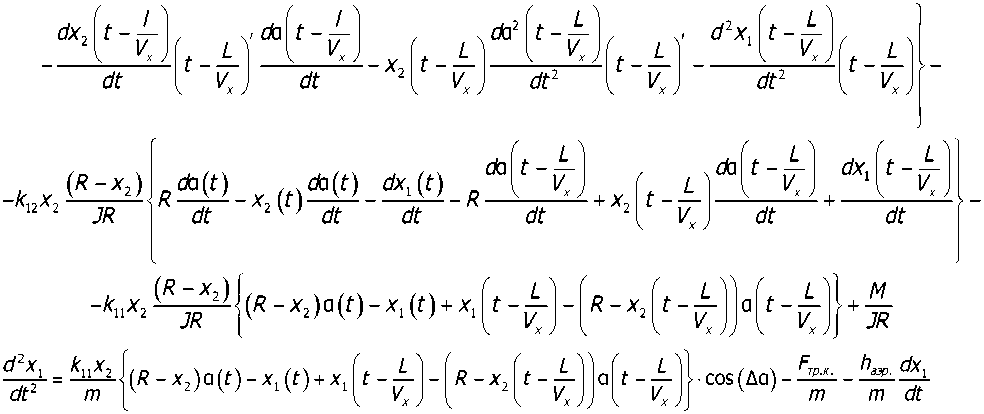
d2x2 _ P dt2 m
1 + к ^1
^dt dx-
т
dt
Да = -
О,
при /Хх
k + k I
--------— X2 m
“2 ‘“A L -----, при -< Д
R
2
Ур.к.
= sign [^-0,01
-mg
V =^L x dt dxt dt
2’ dt2
dxx
Y
dt
J
Результаты моделирования.
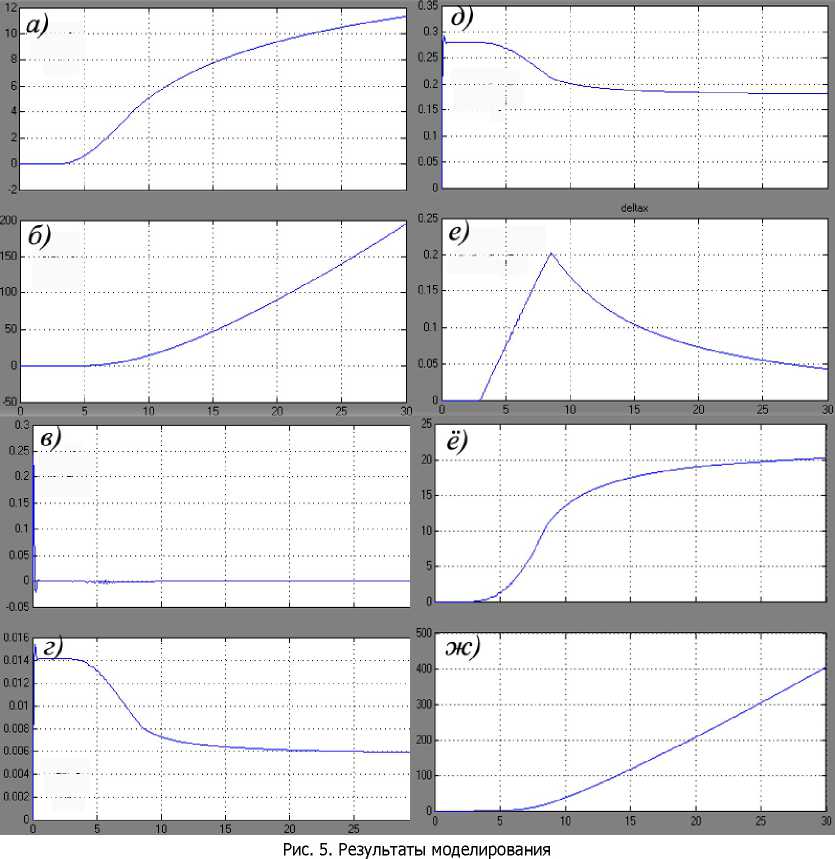
Для оценки реализуемости полученного математического аппарата разработана программная реализация модели в среде Matlab. Привести внешний вид модели не представляется возможным из-за её громоздкости, но некоторые результаты моделирования представлены на рис. 5.
При реализации модели в качестве источника внешнего момента использовался стандартный двигатель постоянного тока, на который подавалось линейно нарастающее напряжение до момента насыщения. В результате, как видно на рис. 5, система в целом устойчива. При этом на рис. 5 представлены следующие характеристики системы: a)xi — тангенциальное перемещение,
dx. . dx,
б) —L — скорость тангенциального движения, в) —- — скорость нормального движения центра
dt dt
масс колеса, г)
хг
— нормальное перемещение центра масс колеса, д)
L
— площадь контакта,
. - . da
е) Дх — проскальзывание, е) о — угол поворота колеса, ж) — — угловая скорость.
dt
Заключение.
В современном описании движения железнодорожного транспорта оценивают эффект проскальзывания как разницу скоростей между линейным движением центра масс колеса и соответствующим ему угловым движением недеформированного колеса [1]. Отличие рассматриваемой модели от существующего подхода и других описаний эффекта проскальзывания [2—9] заключается в том, что вместо разницы скоростей вводится интегральная характеристика смещения за единицу времени контактного взаимодействия. В статье учтены предварительные авторские наработки в области оценки влияния нормальных деформаций в контакте колеса и рельса на длину площадки контакта и, как следствие, на время контактного взаимодействия.
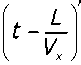
Список литературы Модель связи упруго-вязкого смещения поверхности колеса относительно рельса с тяговыми характеристиками
- Розенфельд, В. Е. Теория электрической тяги/В. Е. Розенфельд и др. -Москва, Транспорт, 1995. -294 с.
- Carte, F. W. On the action of a locomotive driving wheel/F. W. Carte//Proc. R. Soc. -London, 1926. -112 А. -P. 151-157.
- Nielsen, J. B. Tangential contact problem with friction coefficients depending on sliding velocity/J. B. Nielsen, A. Theiler//Proc. 2nd miniconf. on contact mechanics and wear of rail (wheel) systems. -Budapest, 1996. -P. 44-51.
- Knothe, K. Normal and tangential contact problem with rough surfaces/K. Knothe, A. Theiler//Proc. 2nd miniconf. on contact mechanics and wear of rail (wheel) systems. -Budapest, 1996. -P. 34-43.
- Коган, А. Я. Взаимодействие колеса и рельса при качении/А. Я. Коган//Вестник ВНИИЖТ. -2004. -№ 5. -С. 33-40.
- Марков, Д. П. Взаимосвязь коэффициента трения с проскальзыванием в условиях взаимодействия колеса с рельсом/Д. П. Марков//Вестник ВНИИЖТ. -2003. -№ 3. -С. 31-33.
- Харрис, У.-Дж. Обобщение передового опыта тяжеловесного движения: вопросы взаимодействия колеса и рельса/У.-Дж. Харрис и др. -Москва, Интекст, 2002. -408 с.
- Мугинштейн, Л. А. Нестационарные режимы тяги/Л. А. Мугинштейн, А. Л. Лисицын. -Москва, Интекст, 1996. -176 с.
- Марков, Д. П. Коэффициенты трения и сцепления при взаимодействии колёс с рельсами/Д. П. Марков//Вестник ВНИИЖТ. -2005. -№ 4. -С. 3-9.
- Малинин, Н. Н. Прикладная теория пластичности и ползучести/Н. Н. Малинин. -Москва, Машиностроение, 1968. -400 с.
- Крагельский, И. В. Трение и износ/И. В. Крагельский. -Москва, Машиностроение, 1968. -408 с.
- Младов, А. Г. Системы дифференциальных уравнений и устойчивость движения по Ляпунову/А. Г. Младов. -Москва, Издательство МГУ, 1966. -222 с.
- Выгодский, М. Я. Справочник по высшей математике/М. Я. Выгодский. -Москва, Госиздательство технико-теоретической литературы, 1957. -783 с.
- Лапшин, В. П. Модель связи вертикальных деформаций с возникновением циркуляционных сил/В. П. Лапшин//Вестник Дон. гос. техн. ун-та. -2011. -Т. 11. -№ 8 (59). -Вып. 2. -С. 1424-1432.
- Туркин, И. А. Повышение точности позиционирования ротора турбины за счёт учёта свойств фрикционного контакта/И. А. Туркин//Вестник Дон. гос. техн. ун-та. -2011. -Т. 11. -№ 8 (59). -Вып. 2. -С. 1432-1436.


