Модель термоконвекции несжимаемой вязкоупругой жидкости ненулевого порядка. Вычислительный эксперимент

Система, уравнений

k

(1 — AV2)vt = vV2v — (v • V)v+^2 Pi V2wi — gq9 — Vp + f, i=1

0 = V ( V^ v ) ,

^dwL = v + a i w i , a i E R -, l = 1 , k, ∂t

, 9t = жV2 9 — v • V9 + v • q моделирует эволюцию скорости v = (v 1,...,vn), vi = vi(x,t), градиента давления Vp = (pi, ...,pn), pi = pi(x,t) и температуры 9 = 9(x,t) несжимаемой вязкоупругой жидкости Кельвина-Фойгта порядка k > 0, x E Q С Rn, n = 2,3,4 — ограниченная область с границей dЦ класса C^ [1]. Параметры A E R, v E R+ и ж E R+ характеризуют упругость, вязкость и теплопроводность жидкости соответственно; g E R+ — ускорение свободного падения: вектор q = (0,..., 0, 1) — орт в Rn. Пара, метры ei E R+ , l = 1, k определяют время ретардации (запаздывания) давления. Свободный член f = (fi,..., fn), fi = fi(x) отвечает внешнему воздействию на. жидкость. Начально-краевые задачи для моделей термоконвекции были изучены в [2-4].

В области Ц = [0 , п ] х [0 ,п ] рассмотрим систему (1) в виде ( k = 1)

(1 — AV ²) v t = vV ² v — ( v • V ) v—eV ² w — gq9 — Vp,

0 = V • v,

* dw                                                                         (2)

—- = v + aw, a E R -, ∂t

9_t = ж V ² 9 — v • V9 + v • q.

Введем функцию тока, определенную уравнениями v 1

= дд ^,v 2 = -db , ^г^^{е i} = ^{i ( x,}y^,t ) •

Тогда система (2) преобразуется к виду

, ,        4     9 ⁽ ^ V ^{2 i} )    _V7w₍dw 1 ^dw 2

⁽¹ - ^AV ) ^V ^ = ^vVi - W ^{-eV (}W ^- a x )⁺ g⁹ - ’

∂w 1    ∂ψ

' ^aW 1 ’

∂t ∂y

^ = - ^ + aw2 ,a e R .,

∂t ∂x

9 t = $ V ² 9 +

d ( i,9 ) ^{d ( x,}y )

+ T ∂x

Для системы (3) поставим задачу Коши - Бенара i (x, о, t) = i (x, n, t) = v 2 i (x, о, t) = V2 i (x, n, t) = 0, i(о’ У’ t) = i(п У’ t); V2i(0’ У’ t) = V2i(п У’ t)’ 9(x, 0, t) = 9(x, n, t) = 0; 9(0, y, t) = 9(n, y, t), 9(x, y, 0) = 9о(x, y); i(x, y, 0) = io(x, y),

w i ( x, 0 ,t ) = W i ( x,n,t ) = 0; W i (0 ,y,t ) = W i ( n,y,t ) ,

. W i ( x,y, 0) = W i o( x,y ); i = 1 , 2 .

Целью данной статьи является проведение вычислительного эксперимента по исследованию решения задачи (3) , (4) .

Вычислительный эксперимент

На основе теоретических результатов [5] для системы (3) , моделирующей эволюцию скорости, градиента давления и температуры несжимаемой вязкоупругой жидкости Кельвина-Фойгта, в системе компьютерной математики Maple разработана программа [6], которая позволяет:

• 1.    По заданным коэффициентам а, в, X, $ , v на основе метода Галеркина численно находить решение системы.

• 2.    Получить графическое изображение решения системы.

Для реализации вычислительных алгоритмов программы использовались встроенные функции и стандартные операторы языка программирования Maple. Для получения графического изображения подключен пакет plots.

Найдем галеркинское приближение к задаче (4) для системы уравнений (3). С этой целью выберем в качестве базисных функций метода Галеркина собственные функции следующей задачи

_< —V ² V = Xv,

, V ⁽ x ⁰⁾ = V ⁽ x^п ) = ⁰ ’ V ⁽⁰ ’ y ) = V ⁽ П y ) .

Нетрудно получить a ki = П _sin(2 kx ) sin( ly ) , в к1 = n cos(2 kx ) sin( ly ) , yi = ^^ sin( ly ) -ортонормированное в смысле L 2 множество собственных функций. Галеркинское приближение к решению задачи (4) для системы (3) возьмем в виде i = a ( t ) а 11 , 9 = b ( t ) в 11 + c ( t ) Y 2 , w 1 = d ( t ) в 11 + f ( t ) Y 2 , w 2 = g ( t ) в 11 + h ( t ) Y 2 .

На следующем этапе, умножив скалярно уравнения системы (3) на функции а 11 , в 11 , Y 2, получим систему обыкновенных дифференциальных уравнений. Зададим начальные условия из окрестности точки нуль. Затем численно решим задачу Коши для системы обыкновенных дифференциальных уравнений с заданными начальными условиями.

Пример 1. Требуется найти численное решение задачи (3) , (4) при заданных коэффициентах v = 2, а = — 1, в = 2, А = 1, $ = 1, а также получить графическое изображение этого решения.

Умножим скалярно уравнения системы (3) на собственные функции а 11 , в 11 ,Y 2- Получим систему дифференциальных уравнений

• — 5 a( t )(1 + 5 А ) — 25 va ( t ) + 10 вд ( t ) + 19 . 6 b ( t ) = 0 d( t ) — ad ( t ) = 0 , g ( t ) + 2 a ( t ) — ад ( t ) = 0

• < b ( t ) + 5$ b ( t ) + 2 П 2 a ( t ) c ( t ) — 2 a ( t ) = 0 f ( t ) — af ( t ) = 0 , h ( t ) — ah ( t ) = 0 c ( t ) + 4$ c ( t ) — 2^2 a ( t ) b ( t ) = 0 .

Зададим начальные условия из окрестности точки нуль. Пусть a (0) = 0 , 2 ,b (0) = 0 , 1 ,c (0) = 0 , 2 ,d (0) = 0 , 1 , f (0) = 0 , 3 , g (0) = 0 , 2 ,h (0) = 0 , 2. Решим задачу Коши для данной системы уравнений. Графическая иллюстрация решения системы представлена на рисунке. Результаты численного решения частично приведены в таблице.

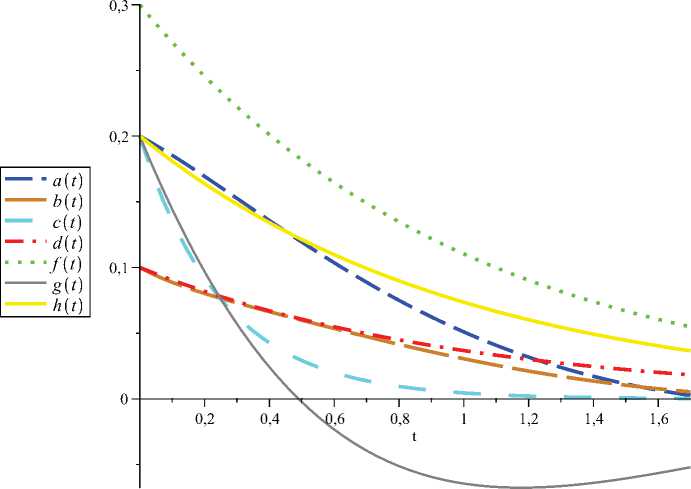
Решение системы при а = — 1 , в = 2 , А = 1 , v = 2 , ш = 1

Автор выражает признательность профессорам Т.Г. Сукачевой и Г.А. Свиридюку за внимание к данным исследованиям и обсуждение результатов.