Модель трансверсально-изотропного сферического слоя для расчета изменения внутриглазного давления при интрасклеральных инъекциях

Одним из современных способов лечения некоторых глазных заболеваний является интрасклеральная инъекция небольшой (до 0,2 мл) дозы лечебного препарата (например, триамцинолона, авастина и т.д.) [1, 2]. За счет кратковременного увеличения внутреннего объема глазного яблока при введении таких инъекций в первый момент происходит резкое увеличение внутриглазного давления. Даже кратковременное увеличение внутриглазного давления выше определенного индивидуального уровня может привести к нарушению кровообращения на сетчатке и в диске зрительного нерва [3]. Важно в каждом конкретном случае оценить возможный уровень изменения внутриглазного давления в результате инъекции и риск для отдельного пациента, а также, возможно, на основе этих данных рекомендовать уменьшенную дозу препарата для отдельных больных (в настоящее время инъекции имеют стандартный объем: 0,05; 0,1; 0,2 мл, определяемый фирмой-производителем).

С точки зрения механики – это задача определения изменения внутреннего давления в оболочке, заполненной несжимаемой жидкостью, при введении дополнительного объема несжимаемой жидкости.

Постановка задачи. Математическая модель

Внешняя оболочка глаза - корнеосклеральная оболочка - состоит из роговицы и склеры, причем склера занимает 93% этой оболочки, поэтому в задачах, связанных с изменением объема глазного яблока под действием внутреннего давления биомеханические свойства склеры играют решающую роль. Роговица в таких задачах обычно не включается в модель, а вся внешняя оболочка глаза рассматривается как состоящая целиком из склеры [4].

При постановке данной задачи и проведении предварительных расчетов авторы пришли к выводу, что расчет изменения внутриглазного давления с использованием различных теорий оболочек, полагающих, что толщина склеральной оболочки остается неизменной, приводит к результатам, которые не очень хорошо согласуются с экспериментальными данными [5]. Вероятно, это связано с тем, что склера является анизотропной (в первом приближении - трансверсально-изотропной [6, 7]) оболочкой, причем модуль упругости склеры в направлении ее толщины на два порядка меньше модуля упругости в тангенциальном направлении [6, 7]. В связи с этим рассмотрим задачу трехмерной теории упругости о деформации сферического слоя с внутренним радиусом R 1 и внешним радиусом R ₂ ( R 1 <р< R ₂), находящегося под действием внутреннего давления Р . Для изотропной сферы эта задача описана, например, в [8, 9].

Как и в [8, 9], из соображений симметрии положим, что в сферической системе координат ( р , ф , 0 ) справедливы равенства:

^ 99 ⁽ Р ) = ° фф ⁽ Р ), ° рр =° рр ⁽ Р ), и

° р9 = ^ рф = ^ 9ф = °.

В этом случае уравнения равновесия приводятся к одному уравнению:

--” + ~(2^ -Q -^СТ9 9) = 0.                           (1) др р' рр ФФ                                             v 7

Закон упругости для трансверсально-изотропного тела в сферических координатах имеет вид [10]:

e =	— (с - E ϕϕ	V° 99 ) -	v' о„, е.	= σ ϕρ
ϕϕ			E ' рр , фр	G'
e θθ =	~ (С 99 - E	^ФФ ) -	V ' Е G , e 9р	= σ θρ G ' ,
е = ρρ	v’г - E , (° 99	'G ) +	1 Е^ ° рр , e Ф9	= σ ϕθ G

Число упругих коэффициентов в этом случае равно пяти [10]: E и E ' -соответственно, модули Юнга при растяжении - сжатии в поверхности изотропии и в направлении, перпендикулярном к ней; v и v ' коэффициенты Пуассона; G ' - модуль сдвига для любой плоскости, перпендикулярной к поверхности изотропии; модуль сдвига для поверхности изотропии G определяется соотношением

G =

2(1 + v )

Упругие коэффициенты удовлетворяют системе неравенств [10]:

I v '^| <

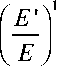
v <  1 -

2 v '² E

E'

Предполагается также, что компоненты вектора перемещения удовлетворяют соотношениям uФ = u8 = °, up = up(р).

В силу этого компоненты тензора деформаций в сферической системе координат примут следующий вид:

e pp

du            u

—^P e = e„„ = —^P e „ = e„ = e = 0 d p ’ ^e фф e 00        . ^e ф0 e 0p e фр °*

Выразим компоненты тензора напряжений через компоненты тензора деформаций и компоненты вектора перемещений:

udu

^ фф = ^ 00 = A^e фф ⁺ Be pp = A — ⁺ B "у¹ .

р udu

°pp= Ceфф+ Depp= C'

p где

A =----- EE ---—, B = A v ', C = 2 A v ', D = A (1 -v ) E 7 E .

E '(1 -v ) - 2( v ')² E

При подстановке этих компонент в уравнение равновесия (1) получается дифференциальное уравнение:

d2 up + 2 duр + 2E(v'-1) uр = ° dp2 р dр E'(1 -v) p21

с граничными условиями:

Срр (R1) = - P, Срр (R 2) = 0.(3)

Решение уравнения (2) имеет вид:

u р ( P . P ) = C ^ + С 2 ( P ) P "  .

где

• 1    лД + 43

  2 E (1 -v ')

  E '(1 -v ) *

  
  

m =---+ -,

Отметим, что в изотропном случае m = 1, так как E = E ', v = v ', в = 2 . Из граничных условий (3) можно получить

P   [(1 -V ) E '- 2 v '² E ]       R m ^{+ 2} R ₂ ^{2 m + 1}

E [( m + 1)(1 -v ) E '- 2 v ' E ] ( R ₂ ^{2 m + 1} - R ^{2 m + 1})^,

C P [(1 -v ) E '- 2 v '² E ]      R m ^{+ 2}

• ²    = E '[ m (1 -v ) E '+ 2 v ' E ] ( R 2 ^{2 m + 1} - R ^{2 m + 1}) ’

Изменение объема исходной сферы, находящейся под действием давления P , можно определить по следующему соотношению:

• 4                  . 4

А V = з п(R + ир (R1, P))3 - з п(R1)3, а отсюда можно вывести и обратную зависимость P = f (А V), характеризующую изменение внутреннего давления от дополнительно введенного объема жидкости.

Результаты расчета и выводы

Для сферического слоя с параметрами R 1 = 11,75 мм, R ₂ = 12,25 мм, E = 14,3 МПа и v = 0,4 - реальными параметрами склеральной оболочки эмметропического глаза (глаза с нормальным зрением), полученными в экспериментальных исследованиях [4, 6], и при начальном значении внутриглазного давления равного 15 мм рт. ст., при различных соотношениях E / E ' для инъекции 0,1 мл получены значения коэффициента Пуассона v ' и изменения внутриглазного давления, приведенные в таблице.

Таблица

Изменение внутриглазного давления при введении инъекции 0,1 мл

Соотношение E / E'	Коэффициент Пуассона v '	P (мм рт. ст.)
1	0,40	70,2
2	0,30	68,8
10	0,15	60,6
100	0,01	56,3
200	0,0075	47,4

Данные таблицы показывают, какое существенное значение имеет учет соотношения трансверсального и нормального модулей упругости склеры. Отметим, что результаты, представленные в предпоследней строке таблицы, наиболее соответствуют экспериментальным данным, полученным при интраоперационном измерении внутриглазного давления тонометром Шиотца сразу после инъекции 0,1 мл препарата тримцинолон [5].

Паликарис ( Pallikaris ) с соавторами [11] на основе прижизненных измерений изменения внутриглазного давления от увеличения объема глазного яблока в группе здоровых лиц приводит экспериментальную линейную зависимость роста внутриглазного давления от объема добавляемой в глаз малыми порциями жидкости. Авторы приводят данные для дополнительных объемов до 0,08 мл. Экстраполяция этих

0,06

0,05

0,04

0,03

0,02

0,01

J

0,02       0,04      0,06       0,08       0,1

Изменение объема полости сферы V, мл

♦ E / E '=1 D E / E '=2 EE / E '=10 EE / E '=100 D E / E '=200

Рис. 1. Зависимость изменения толщины склеральной оболочки от объема введенной несжимаемой жидкости данных для дополнительного объема 0,1 мл при начальном внутриглазном давлении, равном 15 мм рт. ст., дает значение соответствующего изменения внутриглазного давления в 55 мм рт. ст., что хорошо согласуется с данными расчетов, проведенных в статье, при E / E' = 100.

Данные о коэффициенте ригидности корнеосклеральной оболочки глаза, приводимые авторами других прямых манометрических измерений изменения внутриглазного давления от увеличения объема глазного яблока [12-14], хорошо соотносятся с данными работы [11]. Хотя понятие ригидности тканей в офтальмологии и в биомеханике различаются, математическая аппроксимация изменения внутриглазного давления при изменении внутриглазного объема на 0,1 мл по этим экспериментальным данным, видимо, приведет к похожим результатам.

С возрастом ригидность склеральной оболочки возрастает (увеличиваются модули упругости склеры, причем модуль упругости склеры в направлении ее толщины увеличивается быстрее) [6]. Это приводит, видимо, к уменьшению отношения E / E ', и тот же самый объем инъекции в более пожилом возрасте может вызывать более высокий рост внутриглазного давления, чем в молодом возрасте. Кроме того, поскольку упомянутые клинические эксперименты [5, 11] проводились в основном на пожилых пациентах, можно предположить, что отношение E / E ' в глазах молодых людей еще больше, чем 100.

Отметим также, что по соотношению для нормального перемещения можно получить изменение толщины слоя склеры под действием давления P :

A h = u р ( R 2 , P ) - u р ( R 1 , P ).

На рис. 1 показана рассчитанная по представленной математической модели зависимость относительного изменения толщины склеральной оболочки от объема введенной несжимаемой жидкости.

Изменение толщины склеральной оболочки при увеличении внутриглазного давления как один из результатов представленного моделирования, согласуется с имеющимися данными о том, что при открытоугольной глаукоме, глазном заболевании, сопровождающемся, как правило, повышенным уровнем внутриглазного давления, также наблюдается уменьшение толщины склеры [15].

При этом при глаукоме также увеличивается ригидность корнеосклеральной оболочки [16, 17]. Возможно, наблюдавшееся в эксперименте увеличение ригидности склеры при глаукоме [16] также сопровождается уменьшением отношения E / E ' , отличающегося в динамике от физиологического.

Заключение

Необходимость учета трансверсальной анизотропии корнеосклеральной оболочки глаза для конкретных задач моделирования физиологических и патологических процессов в глазу, а также возрастные зависимости значения E / E ' в норме и при патологиях глаза предстоит еще изучить. Первые результаты моделирования изменения внутриглазного давления при интрасклеральных инъекциях показали, что представленный математический аппарат может быть использован для адекватной оценки роста внутриглазного давления в результате инъекции для глаз, имеющих форму, близкую к сферической форме, по известным биометрическим данным.

Представленные результаты для сферического слоя являются основой для решения более общей задачи оценки изменения внутреннего давления при изменении внутреннего объема оболочки эллипсоидальной формы. Такая задача позволит оценивать внутриглазное давление после инъекций в гиперметропических (дальнозорких) и миопических (близоруких) глазах.

Благодарности

Работа выполнена при поддержке РФФИ, грант № 04-01-00258.