Модель управления качеством роботизированных линий розлива на основе локализации неисправностей

Введение, цель

В условиях современной промышленности роботизированные линии розлива играют ключевую роль в обеспечении высокой производительности и качества продукции. Однако повышенная сложность таких систем приводит к увеличению вероятности возникновения не только различных неисправностей, но и аномалий в процессах функционирования ключевых операций производственного процесса, что может негативно сказаться на эффективности производства и качестве выпускаемой продукции. При этом существующие методы контроля функционирования производственных процессов и операций порой не унифицированы и часто не позволяют своевременно и точно локализовать неисправности и аномалии в выполняемой операции, что приводит к простоям и дополнительным затратам [1; 2].

Отсюда возникает актуальная задача в данной области - разработка новых подходов контроля выполнения ключевых операций в автоматизированных производственных линиях которые позволяют не только своевременно вы- являть отклонения от нормального функционирования этих операций, но и точно локализовать место возникновения отклонения или аномалии.

Следует отметить, что в рамках данного исследования качество функционирования роботизированных линий определяется через интенсивность отклонений от идеальных характеристик работы операций, включая вероятность ошибок первого рода (ложные срабатывания) и второго рода (пропуски аномалий).

Математическое моделирование нормального функционирования производственного процесса является основой для локализации и анализа аномальных состояний. В рамках данной работы предлагается модель, описывающая по следовательно сть ключевых операций, выполняемых на роботизированной линии розлива с использованием функций вероятностной оценки нормальных и отклоняющихся значений, где каждое значение соответствует вызову функции на каждом этапе производственного цикла.

По данной проблематике существуют схожие подходы и исследования, например предложен подход к диагностике неисправностей на линиях розлива на основе моделей который включает индивидуальные решения для диагно стики на основе машинных данных. Тестирование на практике показало, что модель обеспечивает до 87,1 % правильных результатов диагностики и признана полезным инструментом для оптимизации работы завода [3]. Данное исследование актуально, так как комплексные производственные линии нуждаются в быстрых и точных инструментах для минимизации времени простоя, однако подход ограничен конкретной настройкой модели под оборудование и может требовать значительной адаптации для других типов линий розлива.

Известны методы онлайн-анализа аномалий с использованием независимого компонентного анализа. Данные исследования демонстрируют методы обнаружения аномалий на основе анализа многомерных сигналов, что в целом помогает выявлять скрытые структуры и предупреждать дефекты в производственном процессе. Такие методы включают независимый компонентный анализ и позволяют обнаруживать отклонения, что может применяться для повышения качества продукции в различных производственных процессах [4–6]. Эти подходы актуальны в современных промышленных системах с множеством датчиков и сенсоров однако они не всегда учитывают временные зависимости в данных, что может ограничить точность выявления неисправностей.

Также разрабатываются и внедряются алгоритмы для работы интеллектуальных систем управления сложными объектами, построенных на основе генетических и роевых подходов [7; 8]. Однако проблема адаптации таких алгоритмов заключается в сложности настройки для специфических производственных условий и необходимости балансировать между глобальным и локальным поиском решений.

В рамках визуального контроля качества современные исследования используют авто-энкодеры для автоматического определения дефектов, что стало особенно актуальным в условиях Индустрии 4.0 (Industry 4.0). Визуальные аномалии можно определять точно и оперативно, однако для точности анализа данных необходимы большие объемы данных и учет разнообразных факторов, что не всегда применимо к малым сериям производства [9–11].

Системы предиктивного технического обслуживания в рамках Индустрии 4.0 все чаще используют цифровые двойники, интегрированные с технологиями искусственного интеллекта, для повышения точности прогнозов и снижения рисков отказов [12; 13]. Выявлено что такая интеграция способствует улучшению диагностики, позволяя точнее прогнозировать возможные неисправности и планировать ремонтные работы, что может существенно уменьшить простои оборудования. Модель предлагаемая в данной работе, использует анализ частотных и временных метрик для точного выявления и локализации неисправностей на уровне отдельных узлов производственной линии. Это позволяет не только своевременно обнаруживать отклонения, но и адаптировать предиктивное обслуживание к специфике конкретного оборудования, что способствует сокращению простоев и снижению затрат на техническое обслуживание.

Исследование Валиахметова и соавторов отличается схожим подходом к обработке временных рядов и диагностике неисправностей используя математические модели для выявления аномалий в сложных производственных системах. Их метод основан на эвристических алгоритмах для анализа данных, в то время как в настоящем исследовании акцент сделан на разработке математической модели управления качеством функционирования роботизированных линий розлива, которая включает локализацию неисправностей и контроль аномалий производственного процесса [14].

Цель исследования состоит в разработке и верификации математической модели для управления качеством функционирования роботизированных линий розлива на основе методов локализации неисправностей и контроля аномалий производственных процессов.

Предлагаемая модель должна обеспечивать своевременное обнаружение аномалий в режиме реального времени; точную локализацию неисправностей до уровня конкретных узлов или функций; масштабируемо сть для применения на производственных линиях различной сложности.

Методы исследования

Для повышения эффективности управления качеством функционирования роботизированных линий розлива необходимо разработать модель, позволяющую детектировать и локализовать неисправности в режиме реального времени. Основой для такой модели является анализ нормального поведения производственной системы и выявление отклонений, связанных с аномалиями в работе оборудования или процессов.

В основе предложенного метода лежит концепция моделирования на основе вызовов функций и анализа отклонений от нормального профиля работы системы. Данная концепция была адаптирована из подхода «Диагностики на основе моделей для локализации неисправностей в программах на языке Си с несколькими тестовыми примерами» и приспособлена для условий роботизированных производственных линий [15]. Исходная модель, предложенная Orvalho et al. (2024), предназначена для локализации неисправностей в программах на языке Си с использованием нескольких тестовых примеров. Основной идеей их подхода является применение модельно-ориентированной диагностики для выявления потенциальных ошибок в коде путем сравнения ожидаемого и фактического поведения программы.

В то время как модель Orvalho et al. фокусируется на программных ошибках, данная адаптация учитывает как программные, так и аппаратные аспекты производственного процесса, а функции в предлагаемой модели представляют не только программные вызовы, но и ключевые операции роботизированной линии розлива.

Предположим, что процесс розлива P можно представить как набор последовательно выполняемых операций O = { o ₁, o ₂, …, o_n }, где каждая операция o_i характеризуется функциональными параметрами, включающими частоту вызова функции f_i , временные параметры выполнения операции T ( o_i ) и спецификацию допустимых значений для обеспечения допустимого уровня качества функционирования операции o_i .

Для более точного анализа поведения системы декомпозируем процесс розлива на отдельные функциональные единицы или исполнительные блоки, соответствующие определенным событиям или действиям. Такие блоки могут быть связаны с конкретными механизмами или модулями оборудования (например дозирование, укупорка, этикетирование).

При этом учитываются следующие допущения:

• 1)    каждая операция o_i является условно независимой и выполняется параллельно или последовательно, с небольшим временным лагом между этапами;

• 2)    в течение нормального периода работы линии частоты выполнения функций f_i сохраняются стационарными;

• 3)    временные параметры T ( o_i ), не зависят от внешних условий, что предполагает работу линии в номинальном режиме при нормальных операционных условиях.

Каждая операция o_i характеризуется рядом параметров, определяющих ее нормальное функционирование:

– средняя частота вызова функции f_i – это показатель, который отражает, как часто функция f_i выполняется за единицу времени в условиях нормальной работы системы;

– среднее время выполнения функции T ( f ) - это ожидаемая продолжительность выполнения функции f_i в пределах операции o_i , которое определяется на основе статистических данных и служит ориентиром для оценки качества выполнения операции;

– диапазоны допустимых отклонений для частоты и времени выполнения функций Δ f_i и Δ T ( f_i ), которые устанавливаются с учетом требований к качеству функционирования роботизированной линии и основаны на предварительном анализе рабочих данных, отражающих допустимый уровень вариативности в работе системы.

Для нормального функционирования процесса сформируем массив значений вызовов функций, где каждому этапу производства соответствует определенный профиль выполнения.

Таким образом, нормальная функция вызова для каждой операции o_i описывается вероятностью выполнения вызова функции p ( f_i ) где f_i – это вызов функции, p ( f_i ) – вероятность выполнения f_i в нормальных условиях.

Формально вероятность успешного выполнения функции f для нормальной работы процесса на линии можно выразить как

Р ⁽ f i ) = n i норм / N ^, где n i норм - количество вызовов функции f i в нормальных условиях; N - общее количество вызовов в период времени T .

При возникновении отклонений от номинальных условий система фиксирует аномальные значения, используя метрику отклонения. Пусть функция вызова f_i в момент отклонения выполняется с частотой n i _откл, тогда отклонение D ( fi ) можно определить как

D ( f i ) = I Р ( f i ) - ( n i откл / N) I, где D ( f_i ) - метрика отклонения для функции f i , рассматриваемая через абсолютное значение отклонения вероятности.

Таким образом, если функция f i обычно вызывается с высокой вероятностью p ( f i ) ~ 1, но в текущем цикле не была вызвана, это может указывать на неисправность. В этом случае метрика вычисляется как

D ( f i ) = Р ( f i ).

Если функция fi обычно вызывается редко Р ( fi ) ~ 0, но в текущем цикле была вызвана, это также может свидетельствовать об аномалии:

D ( fi ) = 1 — Р ( fi ).

Суммарная метрика отклонения для всего процесса на линии розлива рассчитывается как сумма всех индивидуальных метрик отклонений:

n

D общ = Z W i D (Л).

i = 1

где w_i - весовой коэффициент, отражающий значимость функции f_t для общего качества функционирования роботизированной линии. Весовые коэффициенты определяются на основе анализа статистических данных и экспертных оценок.

Для распознавания аномалий в работе системы определяется пороговое значение метрики D порог, выше которого система рассматривается как находящаяся в со стоянии отклонения, требующем вмешательства. Пороговое значение определяется эмпирически или на основе анализа исторических данных, а при превышении этого порога включается алгоритм диагностики и локализации неисправностей.

Когда значение D общ превышает пороговое значение D порог , система рассматривает это состояние как потенциально аномальное, требующее вмешательства оператора или корректирующих действий.

Суммарная метрика отклонения D общ анализируется по следующим критериям:

• -    если D общ <  D порог , система функционирует в нормальном режиме;

• -    если D общ >  D порог , возникает состояние, требующее корректирующих действий.

Метрики отклонений для каждого вызова функции D ( f_i ) анализируются для локализации конкретного этапа операции O i , связанного с вызовом функции fi , что позволяет выявить участок процесса, вызвавший отклонение.

Для учета временных характеристик работы линии вводится функция распределения вероятности времени выполнения операций T ( f_i ), описывающая среднюю и дисперсию времени выполнения функции f_i .

Если обозначить нормальное время выполнения функции как ц( f_t ) и его стандартное отклонение как о( f i ), то при отклонении временного параметра T ( f_i ) от нормы вводится временная метрика отклонения TD ( f_i ), т. е. если время выполнения функции T ( f_i ) отклоняется от среднего значения ц( f ) более чем на допустимое стандартное отклонение о( f i ), то вводится временная метрика отклонения:

T D ( fi ) =

T ( fi ) — Ц ( fi ) a ( fi )

где T( fi), - время выполнения функции fi в аномальном цикле.

Итоговая метрика отклонения D итог для производственного цикла интегрирует как ча- стотные, так и временные параметры:

n

D итог = аОобщ +PZTD (U i=1

где а и в - коэффициенты, определяющие вклад каждой метрики в итоговое значение. Данные коэффициенты подбираются на этапе калибровки системы и зависят от конкретных требований к качеству и надежно сти производственного процесса.

Таким образом, процесс локализации неисправностей включает следующие этапы:

• 1)    сбор данных о вызовах функций и их временных характеристиках;

• 2)    сравнение фактических данных с эталонной моделью нормального функционирования;

• 3)    вычисление метрик отклонений (для каждой функции f_i рассчитываются метрики D ( f_i ) и T ( f_i ));

• 4)    идентификация аномалий (функции с наибольшими значениями метрик D _итог( f_i ) рассматриваются как потенциальные источники неисправностей;

• 5)    локализация неисправностей через анализ операций o_i , связанных с выявленными функциями f_i для определения конкретных узлов или компонентов системы, вызывающих аномалии;

• 6)    анализ дерева вызовов (исследуется дерево вызовов для выявленных функций, чтобы определить причинно-следственные связи и локализовать неисправность в конкретном компоненте или узле оборудования).

В роботизированных линиях розлива часто присутствуют группы узлов или механизмов выполняющих идентичные функции (например, несколько параллельных дозаторов или укупорочных машин). Для повышения эффективности моделирования и снижения объема вычислений предлагается использовать подход агрегирования моделей для однородных групп оборудования.

При этом для каждой группы узлов формируется обобщенная модель нормального функционирования, которая учитывает статистические данные, собранные со всех узлов группы. Вероятности вызовов функций p ( f_i ) и статистические характеристики времени выполнения μ( f_i ), σ( f_i ) рассчитываются на основе объединенных данных, что позволяет получить более точные оценки за счет увеличения выборки.

Для обеспечения высокой скорости реакции системы на возникновение аномалий предлагается использовать параллельные вычисления при обработке данных и вычислении метрик отклонения. Каждый узел производственной линии выполняет вычисления метрик D( fi) и T( fi) независимо и параллельно с другими узлами. Это позволяет масштабировать систему без увеличения времени обнаружения аномалий.

Техническая реализация параллельной обработки может быть основана на использовании встроенных вычислительных модулей или контроллеров, способных выполнять необходимые вычисления в реальном времени. При необходимости результаты вычислений могут передаваться на центральный сервер для дальнейшего анализа, однако основная обработка данных производится на уровне узлов.

Результаты и дискуссия

Для подтверждения эффективности предложенной модели было проведено симуляционное моделирование процесса розлива с внедрением механизмов детектирования и локализации неисправностей. В ходе моделирования были учтены реальные параметры производственного оборудования и технологического процесса.

Моделируемая линия розлива состоит из четырех основных узлов, каждый из которых выполняет строго определенную операцию. Все операции имеют свои параметры и важность для производственного процесса, что отражено в весовых коэффициентах. Ниже приведено детальное описание каждого узла и его функции.

Первый узел, выполняющий операцию дозирования, отвечает за наполнение тары жидкостью до определенного объема. Все операции является основополагающей для обеспечении необходимого уровня качества продукции, так как даже небольшие отклонения в дозировании могут существенно повлиять на конечный продукт. Для данной функции ( f ₁) были выбраны следующие параметры:

• – средняя частота вызова p _норм( f ₁) = 0,98 поскольку этот узел должен работать почти безотказно, чтобы обеспечить непрерывность и высокий уровень качества функционирования операции;

  – среднее время выполнения μ( f ₁) = 1,0 с с стандартным отклонением σ( f ₁) = 0,05 с что отражает качество работы узла; такое время выполнения выбрано на основании типичного времени, необходимого для заполнения тары до необходимого уровня

с минимальным разбросом, что обеспечивает консистентность дозирования;

– весовой коэффициент w ( f ₁) = 1,0, так как точность дозирования является критической для качества продукции.

Второй узел выполняет операцию укупорки, закрывая тару крышкой, что важно для обеспечения герметичности и защиты продукции. Надежность и правильность выполнения укупорки обеспечивают безопасность продукции на этапе хранения и транспортировки.

Для функции f ₂ данного узла установлены следующие параметры:

– средняя частота вызова p _норм( f ₂) = 0,95 что указывает на незначительно более низкую частоту успешного выполнения по сравнению с узлом дозирования;

– среднее время выполнения μ( f ₂) = 1,5 с со стандартным отклонением σ( f ₂) = 0,1 с, отражающее допустимую вариативность;

– весовой коэффициент w ( f ₂) = 0,9, так как данная операция влияет на герметичность продукции, укупорка критически важна для герметичности, но имеет меньший весовой коэффициент по сравнению с дозированием так как она оказывает меньшее влияние на фактический объем продукта в таре.

Третий узел осуществляет нанесение этикеток на тару. Эта операция не влияет напрямую на конечные потребительские свойства сырья, однако она критически важна для ее идентификации и соответствия стандартам маркировки. Параметры функции f ₃ определены следующим образом:

– средняя частота вызова p _норм( f ₃) = = 0,92, что также указывает на незначительно более низкую частоту выполнения по сравнению с узлом дозирования, по скольку эта операция влияет не на саму продукцию а только на внешний вид и информационные данные упаковки, в случае редких пропусков этикетирования продукция остается пригодной;

– среднее время выполнения μ( f ₃) = 1,2 с со стандартным отклонением σ( f ₃) = 0,08 с, этикетирование занимает меньше времени, чем укупорка, и обычно варьируется в пределах небольшого диапазона, отраженного в значении стандартного отклонения;

– весовой коэффициент w ( f ₃) = 0,85, поскольку правильное этикетирование необходимо для презентации и информативности продукции.

Завершающий узел выполняет операцию упаковки тары для последующей транспортировки. Хотя данная операция завершает производственный процесс, от ее эффективности зависит общая производительность линии. Параметры функции f ₄ заданы следующим образом:

– средняя частота вызова p _норм( f ₄) = 0,90 что также указывает на незначительно более низкую частоту выполнения по сравнению с узлом дозирования;

– среднее время выполнения μ( f ₄) = 1,8 с со стандартным отклонением σ( f ₄) = 0,12 с в силу того, что упаковка – самый длительный процесс среди операций на линии, так как он включает укладку и стабилизацию тары для последующей транспортировки, стандартное отклонение относительно высоко, отражая допустимую вариативность в работе этого узла;

– весовой коэффициент w( f ₄) = 0,8, поскольку упаковка завершает процесс и оказывает меньшее влияние на качество самого продукта, ее весовой коэффициент несколько ниже, однако, учитывая ее важность для логистики, параметр остается достаточно высоким.

Цель симуляционной модели – выявить отклонения от нормального функционирования роботизированной линии розлива и оценить эффективность методов обнаружения аномалий.

Методология симуляции заключается в том, что для каждой операции (дозирование укупорка, этикетирование и упаковка) модель генерирует данные, которые включают время выполнения функций и частоту вызова основанные на нормальном распределении с параметрами, заданными для каждого узла.

При моделировании нормальных циклов работы данные для каждого узла создаются с использованием вероятностей вызова функций и среднего времени выполнения.

Для моделирования аномалий модель искусственно вводит отклонения в некоторых операциях, чтобы проверить, насколько точно система способна выявлять неисправности. Аномалии включают:

– пропуск функции (например, функция дозирования не выполняется, что вызывает отклонение);

– увеличение времени выполнения (например время выполнения укупорки превышает норму).

Модель анализирует функционирование линии розлива, рассчитывая метрики отклонений для каждой операции. Метрики отклонений позволяют количественно оценить отклонения на уровне каждой функции.

Чтобы проверить модель, были разработаны два набора данных:

– нормальные циклы (1000 циклов), где все узлы работают в пределах допустимых значений;

– аномальные циклы (25 циклов), в которых присутствуют отклонения. Эти отклонения включают отсутствие вызова функций и увеличение времени выполнения.

Модель анализирует каждый цикл, вычисляя итоговую метрику отклонения для всех узлов. Если итоговая метрика отклонения D _итог превышает пороговое значение D _порог, цикл считается аномальным и система фиксирует срабатывание выявление отклонения/аномалии.

Пороговое значение метрики отклонения D _порог, используемое для определения аномального состояния цикла, установлено на уровне 2,0.

Это значение было выбрано на основе анализа эмпирических данных и проведения предварительных тестов на моделируемой линии. Выбор порога ориентирован на минимизацию ложных срабатываний (false positives) сохраняя при этом высокую чувствительность к фактическим отклонениям.

При этом значение D _порог может быть скорректировано в зависимости от особенностей конкретной производственной линии и ее требований к надежности.

В итоговой метрике отклонения используются коэффициенты α = 0,7 и β = 0,3, отражающие значимость частотной и временной метрик отклонения соответственно. Выбор этих значений обусловлен высокой важностью временных характеристик для работы роботизированной линии розлива с номинальным уровнем качества функционирования ключевых операций. Коэффициент α установлен на уровне 0,7, чтобы частотная метрика оказала большее влияние на итоговую метрику в случаях значительного отклонения частоты вызова функции, так как пропуски в вызове функции часто указывают на критические сбои. В то же время коэффициент β (0,3) позволяет учесть отклонения во времени выполнения функции которые могут свидетельствовать о снижении производительности или появлении неполадок.

Для оценки адекватности разработанной модели будут использоваться следующие показатели:

– чувствительность (True Positive Rate – TPR), показывающая способность модели корректно выявлять аномальные циклы; она рассчитывается как отношение числа правильно определенных аномальных циклов к общему числу фактически аномальных циклов;

– специфичность (False Positive Rate – FPR), указывающая на вероятность ложного срабатывания модели, т. е. классификации нормального цикла как аномального; специфичность важна для минимизации ложных тревог, которые могут привести к ненужному вмешательству в работу линии.

Эти показатели позволят всесторонне оценить точность модели и ее пригодность для практического использования.

Для выполнения симуляционного моделирования и расчета метрик использовалась среда Python 3.12 с библиотеками NumPy версии 1.21 и Matplotlib версии 3.4. Выполнение моделирования и построение графиков организовано в Jupyter Notebook, что обеспечивает гибкость и удобство при обработке и анализе данных. Выбор этой среды обусловлен ее совместимостью с научными библиотеками Python и ее широким применением в инженерных исследованиях.

Основные параметры моделирования представлены в таблице. В ней отражены частоты вызова, средние значения времени выполнения и стандартные отклонения для каждой функции, а также весовые коэффициенты, которые учитывают значимость каждой операции в рамках производственного процесса. Эти параметры были выбраны с учетом надежности важности и характеристик каждой операции что позволяет модели точно отражать условия работы производственной линии и своевременно выявлять аномалии.

Параметры симуляционного моделирования Parameters of simulation modeling

Узел	Операция ( f ( oi ))	Средняя частота вызова p норм( fi )	Среднее время выполнения μ( f 2), с	Стандартное отклонение σ( f 2), с	Весовой коэффициент w ( fi )
1	Дозирование	0,98	1,0	0,05	1,0
2	Укупорка	0,95	1,5	0,1	0,9
3	Этикетирование	0,92	1,2	0,08	0,85
4	Упаковка	0,90	1,8	0,12	0,8

Предложенная модель направлена на детектирование отклонений и неисправностей внутри производственной линии розлива в рамках заданных параметров. Тем не менее она обладает рядом ограничений:

– модель не учитывает возможные внешние воздействия (такие как изменения температуры или влажности), которые могут оказывать влияние на работу линии, в реальных условиях такие факторы могут приводить к сбоям, которые модель не сможет предсказать;

– модель ориентирована на наиболее вероятные отклонения, но может не учитывать редкие или уникальные виды сбоев, которые не подпадают под заданные закономерности;

– в случае увеличения числа узлов или функций текущие значения параметров могут потребовать корректировки, чтобы сохранить точность и чувствительность модели.

Эти аспекты необходимо учитывать при внедрении модели в производственные условия, так как ее точность и надежность могут зависеть от реальных условий эксплуатации.

На рис. 1–3 представлены ключевые результаты симуляции, включая распределение итоговой метрики отклонений для различных типов циклов, анализ ложных и истинных срабатываний, а также временные характеристики выполнения операций при возникновении отклонений. Эти графики помогают наглядно оценить качество модели и ее применимость для диагностики и предсказания сбоев в реальных производственных условиях.

На рис. 1 представлено распределение значений итоговой метрики отклонений D _итог для нормальных и аномальных циклов производственного процесса. По оси абсцисс

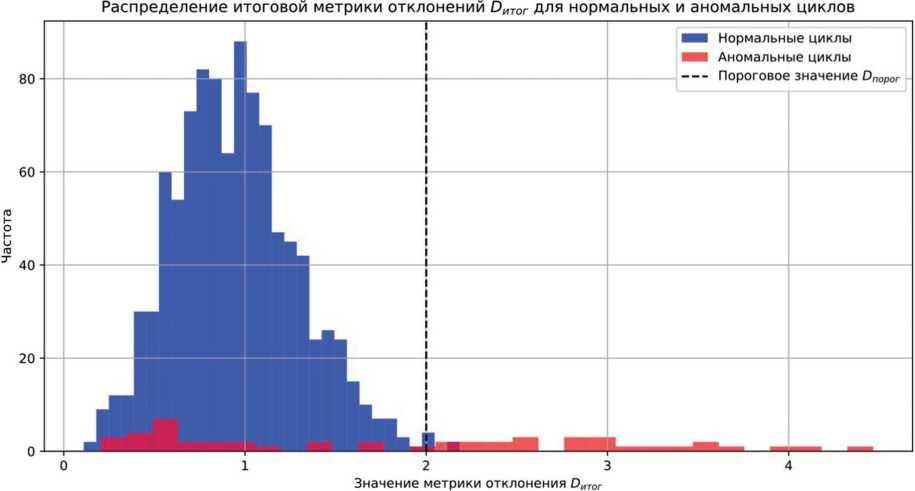
Рис. 1. Распределение значений итоговой метрики отклонений D _итог для нормальных и аномальных циклов моделируемого производственного процесса роботизированной линии розлива

Fig. 1. Distribution of values of the final deviation metric D _total for normal and abnormal cycles of the simulated production process of a robotic filling line

отложены значения метрики D _итог, а по оси ординат – частота их возникновения.

На рис. 1 нормальные циклы, показанные в синем цвете, сгруппированы преимущественно в области низких значений метрики D _итог, что указывает на соответствие процесса установленным параметрам и отсутствие значительных отклонений. Аномальные циклы, выделенные красным цветом, имеют более высокие значения D _итог, что позволяет дифференцировать их от нормальных на основе метрики. Пороговое значение D _порог обозначенное пунктирной линией, является граничным значением, превышение которого указывает на аномалию. Как видно из графика большинство нормальных значений остаются ниже этого порога, в то время как аномальные циклы имеют значения, превышающие установленное пороговое значение.

На рис. 2 представлена гистограмма, отображающая количество ложных срабатываний (False Positive) и корректно выявленных аномалий (True Positive) в процессе симуляционного моделирования.

Ложные срабатывания (F alse Positiv e) составляют 5 случаев, что соответствует ситуации, когда нормальные циклы ошибочно классифицированы как аномальные. Этот показатель свидетельствует о высокой специфичности модели и ограниченном числе ложных тревог, что минимизирует ненужное вмешательство в работу линии.

Корректно выявленные аномалии (True Positive) составляют 24 случая, что отражает способность модели точно определять отклонения и указывать на реальные аномальные состояния в процессе. Высокое значение этого показателя подтверждает высокую чувствительность модели.

На рис. 3 представлено распределение времени выполнения функций f ₁ (дозирование), f ₂ (укупорка), f ₃ (этикетирование) и f ₄ (упаковка) в аномальных циклах моделируемой производственной линии.

На рис. 3 функция f ₁ (дозирование) показывает относительно устойчивое время выполнения с незначительными вариациями, что указывает на высокие показатели качества выполнения операции даже при аномальных циклах. Функция f ₂ (укупорка) демонстрирует больший разброс времени выполнения, что может свидетельствовать о повышенной чувствительно сти к отклонениям в процессе укупорки. Функция f ₃ (этикети-

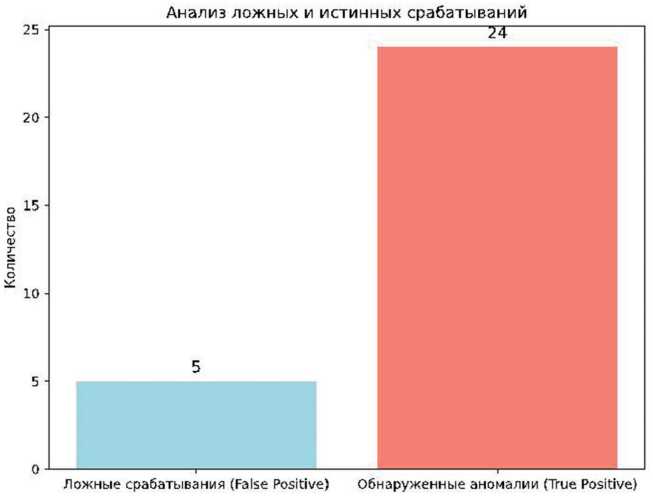
Рис. 2. Гистограмма ложных срабатываний и истинных аномалий, обнаруженных в ходе моделируемого производственного процесса роботизированной линии розлива

Fig. 2. Histogram of false positives and true anomalies detected during the simulated production process of a robotic filling line

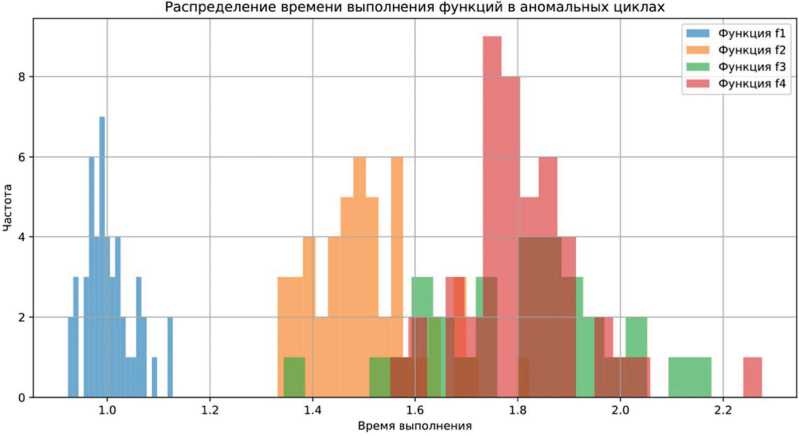
Рис. 3. Распределение времени выполнения операций в аномальных циклах для функций f ₁ (дозирование), f ₂ (укупорка), f ₃ (этикетирование), f ₄ (упаковка)

Fig. 3. Distribution of operation times in abnormal cycles for functions f1 (dispensing), f2 (capping), f3 (labeling), f4 (packaging)

рование) показывает вариативность времени выполнения в пределах от 1,0 до 1,8 с, что отражает возможные неполадки в операциях этикетирования в аномальных циклах. Функция f ₄ (упаковка) также демонстрирует широкий диапазон времени выполнения, что характерно для финальной стадии производственного процесса. Увеличение времени выполнения этой операции может быть связано с накоплением незначительных отклонений на предыдущих этапах, что влияет на упаковку. Таким образом, распределение времени выполнения каждой функции позволяет оценить временные характеристики операций и выявить функции, наиболее подверженные влиянию аномальных со стояний. Это помогает локализовать узлы, требующие более тщательного контроля в условиях отклонений от нормы.

Для оценки адекватности и точно сти разработанной модели были использованы следующие показатели:

– чувствительно сть (True Positive Rate – TPR) – показатель, который определяет способность модели правильно выявлять аномальные циклы, рассчитывается как отношение числа правильно обнаруженных аномальных циклов (True Positives) к общему числу фактически аномальных циклов;

– специфичность (True Negative Rate – TNR) – показатель, который рассчитывается как отношение числа правильно обнаруженных нормальных циклов (True Negatives) к общему числу фактически нормальных циклов;

– ложноположительный уровень (False Positive Rate – FPR) указывает на вероятность того, что модель ошибочно классифицирует нормальный цикл как аномальный и рассчитывается как отношение числа ложноположительных срабатываний (False Positives) к общему числу фактически нормальных циклов.

В результате этого количество правильно классифицированных нормальных циклов составило 99,5 %, а ложноположительный уровень составил 0,5 %. Это хорошие показатели, но они действительны только в условиях действующих ограничений модели, описанных выше.

При этом чувствительность модели оказалась в районе 96 % (всего за аномалии модель приняла 24 (+5 ложных) событий из 25 заданных в модель, на 1000 циклов), что указывает на то, что модель определяет значительную часть аномалий. Снижение порогового значения метрики отклонения может увеличить число корректно выявленных аномальных циклов, однако следует внимательно контролировать возможное увеличение количества ложных срабатываний. Важно найти оптимальный баланс между чувствительностью и специфичностью модели, чтобы обеспечить надежное обнаружение аномалий без существенного роста числа ложных тревог.

Также рекомендуется пересматривать весовые коэффициенты α и β, определяющие вклад частотной и временной метрик в итоговую метрику отклонения на основании конкретного производственного процесса и исторических данных. Например, увеличение значения β может усилить влияние временных характеристик операций на итоговую метрику и повысить чувствительность модели к аномалиям, связанным с изменениями времени выполнения функций. Это особенно актуально для функций, показавших большую вариативность в аномальных циклах, таких как укупорка и этикетирование.

Заключение

В ходе проведенного исследования была разработана математическая модель для управления качеством функционирования роботизированных линий розлива, основанная на методах локализации неисправностей и контроля аномалий производственных процессов. Модель описывает производственный процесс как последовательность функций с вероятностными характеристиками и вводит метрики отклонений для количественной оценки отклонений от нормального функционирования. Симуляционное моделирование, проведенное с использованием реальных параметров производственного оборудования и технологических процессов, подтвердило эффективность предложенной модели. Результаты показали что модель обладает высокой специфичностью (99,5 %) и высокой чувствительностью (96 %) в выявлении аномальных циклов. Это свидетельствует о ее пригодности для практического применения в условиях реального производства.

Модель может быть интегрирована в существующие системы автоматизированного управления производством с использованием данных, собираемых с помощью датчиков и контроллеров на линии розлива. Для успешного внедрения модели рекомендуется провести начальную калибровку и настройку параметров на основе данных конкретного производства. Это включает определение пороговых значений метрик отклонений и установление весовых коэффициентов для функций. Обучение инженерно-технического персонала по интерпретации результатов и принятию решений на основе метрик также является важным шагом для эффективного применения модели.