Модель управления процессом обучения в ИОС

В рабочей программе Евросоюза FP7 на 2009-2010гг. по информационным и коммуникационным технологиям указывается, что адаптивные обучающие системы - это инновационные решения, базирующиеся на технологиях искусственного интеллекта, и способные самонастраивать свою работу оптимальным образом, поддерживать и реагировать на действия обучаемых и учителей, используя информацию об их поведении.

Исследование, развитие и совершенствование архитектуры интеллектуальных обучающих систем (ИОС) находится в центре внимания многих исследователей [1,2]. Одним из основных направлений проводимых работ является решение проблемы адаптивного управления процессом обучения. В случаях, когда в алгоритмах управления используются дидактические принципы обучения, инвариантные к предметной области (ПО) обучения, могут быть разработаны инструментальные средства проектирования ИОС. Педагог, использующий такие средства в конкретной ПО должен обеспечить параметрическую настройку этих принципов к ПО и конкретным обучаемым для обеспечения адекватности управления обучением в проектируемой ИОС.

В результате анализа ряда теорий обучения выделен следующий ряд принципов организации обучения, инвариантных к ПО обучения.

Процесс обучения рассматривается как управляемый и контролируемый процесс решения учебных задач. Определение свойств учебных задач и выдача подкреплений должны осуществляться на основе идентификации умений обучаемого на каждом шаге обучения. В процессе обучения должен соблюдаться принцип перехода от решения простых учебных задач к сложным. Переход к усвоению нового учебного материала осуществляется в случае успешного усвоения предыдущего материала. В процессе обучения должна осуществляться стабилизация субъективной степени трудности учебных задач для каждого обучаемого.

Основные понятия

Формализация выделенных принципов осуществляется следующим образом.

Экспертом-педагогом разрабатывается алгоритмическое предписание, описывающее пути решения учебных задач в заданной ПО обучения.

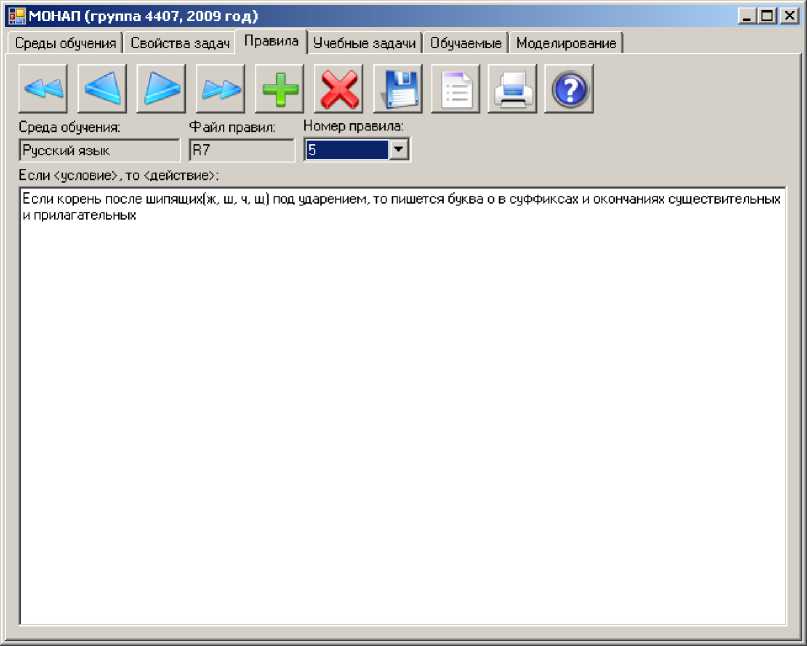
Разработка алгоритмического предписания является, в общем случае, слабоформализуемой, многокритериальной задачей. В результате анализа предметной области обучения выбираются базовые (первичные) элементы, представляющие собой простые понятия (концепты), на основе которых строится рассматриваемый учебный материал. При этом некоторые понятия, являясь базовыми для одной предметной области, в другой могут оказаться сложными, производными понятиями. С учетом выбранных базовых элементов и на основе структурно-алгоритмического анализа деятельности по решению задач определенного класса осуществляется выделение типовых операций, составляющих содержание рассматриваемой деятельности. Под типовой операцией понимается законченная по смыслу, учитывающая специфику предметной области обучения операция, предполагающая элементарные действия над первичными элементами (концептами). Обучение учащихся алгоритмам решения определенных задач осуществляется через управляемое и контролируемое выполнение учебных задач. Например, в ИОС грамматике немецкого языка, спроектированной с помощью инструментальных средств серии MONAP, концептами являются: артикль, род, число, падеж и т.д., а одна из операций, описывающих склонение прилагательных, представлена в виде правила: “ЕСЛИ перед прилагательным и существительным стоит определенный артикль der или одно из местоимений dieser, jener, solcher, jeder, welcher и определяемое существительное мужского рода, ТО окончанием прилагательного является –е” [3,4].

На рисунке 1 представлено формирование набора операций (правил) при проектировании ИОС грамматике русского языка.

Множество типов операций, выполняемых обучаемым при решении задач заданной ПО обучения и соответствующих алгоритмическому предписанию, обозначается через Y = [ у 1 , y ₂,..., y j ,..., y J ] .

В качестве основного компонента оверлейной модели навыков/умений обучаемого, используется вектор:

P (к) = [ P1( k ), P2( к ),..., P,.( к),..., Pj (к)]                                (1)

где: P j ( к ) - вероятность правильного применения операции y j. на к -м шаге обучения ( j = 1,2,..., J ).

Сложность задачи, выданной на к -м шаге обучения, описывается вектором L ( к ) :

L(к) = [L (к\L2 (к),...,Lj (к),...,Lj (к)]

где: L j ( к ) - число операций y j. , использование которых необходимо при выполнении задачи.

Мера трудности задачи T ( к ) вводится как средняя доля ошибок, ожидаемых при выполнении задачи, т.е.:

t ( к ) = MATM S ( к )

где: S(k) = £L/k);

J

MAT ( к ) - математическое ожидание числа ошибок при выполнении задачи;

МА T(к) = У [1 - Pj (к)] х L j (к) = £ q j (к) х Lj (к)              (4)

j = 1                                    j = 1

где: q j ( к ) - вероятность неправильного применения операции y j на k-м шаге обучения.

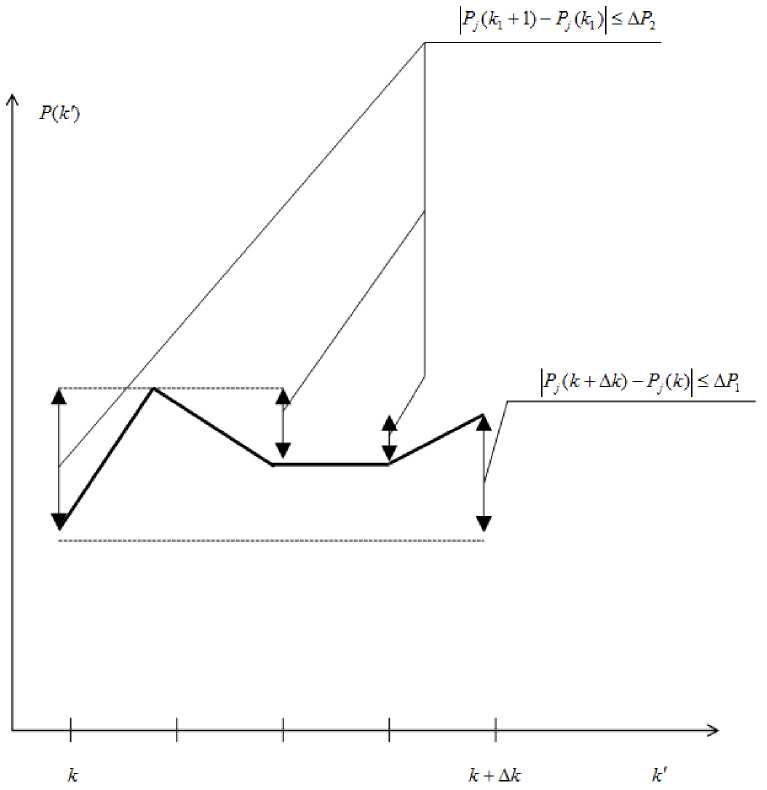
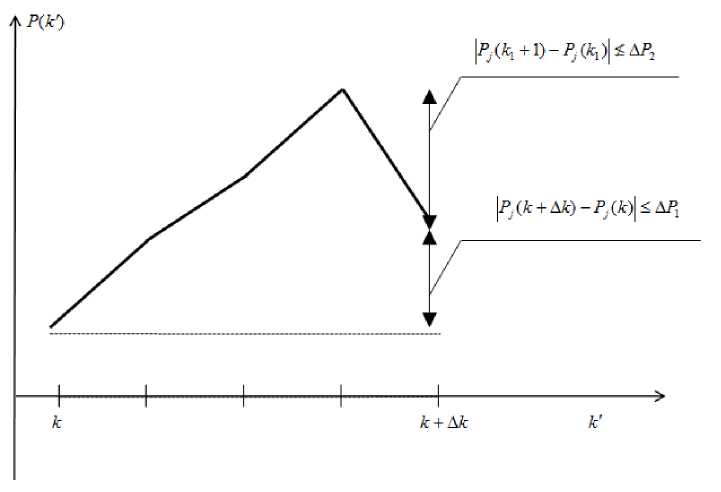
В соответствии с ассоциативно-рефлекторной теорией усвоения необходимо стремиться к тому, чтобы на каждом шаге обучения выполнялось неравенство (стабилизация субъективной степени трудности):

| Топт — T (к )

AT - размер интервала.

Целью обучения является достижение заданного уровня обученности в каждом классе задач ПО обучения при одновременной минимизации времени обучения t (экстремальная цель), где уровень обученности определяется следующим образом: оценка вероятности правильного применения операции yj при выполнении задачи требуемой сложности S_КОН должна удовлетворять неравенству:

Pj (к) - PjKOH                                      (6)

Если достигнут заданный уровень обученности, то обучение заканчивается.

Если хотя бы в одном классе задач ПО обучения имеет место одно или оба из неравенств в следующей системе:

Pj (к) < PjKOH ; I S (к) < S КОН ,

то обучение продолжается.

На каждом шаге обучения, начиная с (к + A к )-го (к = 1,2,...) производится проверка на аварийное окончание. Аварийное окончание обучения осуществляется, если хотя бы для одной операции имеет место система неравенств:

/ j к + A к) — Pj( к )| < AP.; |P(к 1 +1) — P(к 1)|

где: Aк - предаварийное (критическое) число шагов обучения, во время которых характеристики обучаемого могут не улучшаться;

AP1 - задает первый интервал изменения значений элементов вектора P(к) ;

к 1 - изменяется от к до (к + Aк — 1), то есть второе неравенство системы в свою очередь задает систему неравенств;

AP2 - задает второй интервал изменения значений элементов вектора P(к) .

Условия аварийного окончания иллюстрируются на рис.5 (где к ' = 1,2,..., к,...).

Необходимость использования системы неравенств для описания аварийного окончания вызвана тем, что моделью обучения предусматриваются ситуации, когда Pj( к 1 +1) < Pj (к 1) , вызванные, например, забыванием (была значительная пауза в обучении), слабой мотивацией, усталостью и другими "стрессовыми" ситуациями. Эти ситуации не должны вести к аварийному окончанию.

Причиной аварийного окончания является либо слабая подготовка, либо неэффективность обучающих воздействий (комментариев к ошибкам), либо и то, и другое.

Нарушение второго неравенства системы предотвращает аварийное окончание обучения в случае, когда уровень знания обучаемого увеличивался, но произошел неожиданный спад, величина которого больше значения AP2 ("порога стресса"), и выполнилось первое неравенство системы, являющееся необходимым условием аварийного окончания (рис.6), где к' = 1,2,...,к,...).

Рис. 5 Аварийное окончание

Рис. 6 Продолжение обучения

Идентификация (оценка) навыков/умений обучаемого

В предлагаемой модели обучения определение Pj (к) осуществляется следующим образом[5,6]. Для каждой операции yj вводится N гипотез Hi (i = 1,2,...,N) , соответствующих N состояниям обученности. Каждому i -му состоянию  обученности  соответствует условная вероятность   P (Aj./Hi.)

правильного применения операции yj в каждом из Lj ее применений, равная i

N +1

Гипотезы Hi образуют полную группу несовместных событий, т.е.

имеет место:

N

Z Pj = 1-

где: Pj. - вероятность гипотезы Hi для операции yj..

Число состояний обученности зависит от необходимой точности определения состояния обученности. Значение N задается экспертом-педагогом и используется, кроме того, для определения значения PjKOH

равного

N

N +1.

На каждом шаге обучения наблюдается событие Bj (к), состоящее в правильном применении j -й операции M j (к) раз из Lj (к) заданных.

Эта информация служит для перерасчета распределения вероятностей гипотез Pj с помощью формулы Бейеса.

Каждый к -й шаг обучения характеризуется априорным и апостериорным распределениями вероятностей гипотез о состояниях обученности Pij (к) и Pj (к), связанных между собой следующей зависимостью:

P,_(к) = ^Pj(^к)^хP (,^к >/H) ''      у?» (к) х P (B,( к),/H,)

s=1

где: P (B , (к) J Hi) - определяется по теореме Бернулли, т.е.

?(в,(к)/H) = cLM;" XP(Aj/H,)Mj(к) X(1 -P(Av/H,))jк)“•'к)

CM!(к)                   „ Т1

L (_к) — число сочетаний из L, (к) по M , (к).

Учитывая, что априорное распределение вероятностей гипотез на к -м шаге совпадает с апостериорным распределением на (к — 1 )-м шаге, т.е. имеет место:

P°( к) = P( к — 1)

формулу (14) можно переписать в виде, который подчеркивает ее рекурсивный характер (учитывается вся история обучения), а именно:

.        P *( к — 1) x P (B,(к)/H)

Pj (к) = _j-

У Pj( к — 1) X P (в, (к)/H,)

s=1

Вероятность правильного применения операции у , на к -м   шаге определяется по формуле полной вероятности:

N

P(A, (к)) = £ Pj(к) x P(AjlH_t)                      (13)

i=1

Окончательная оценка P, (к) получается приведением значения, вычисленного по формуле, до введенных состояний обученности. Осуществление на к -м шаге обучения контроля ошибок и выдачи необходимых объяснений позволяет вести прогнозирование вероятности правильного применения операции yj на (к + 1)-й шаг обучения:

P, (к + V к) = V x P, (к)

где: V определяется следующим образом:

V=J^p.k)L

P,( к — 1)

Прогнозирование вводится после первых двух шагов обучения.

Выводы

Для построения рассмотренной модели введены и формализованы следующие основные понятия: модель обучаемого, сложность учебной задачи, цель обучения, предаварийное число шагов обучения, «порог стресса состояние обученности, коэффициент прогнозирования обученности. В модели обучения предусмотрена возможность аварийного окончания обучения в случае, когда процесс обучения не является эффективным, что оптимизирует затраты на его проведение. Практическая ценность указанной модели заключается в обеспечении возможности разработки на ее основе инструментальных средств проектирования ИОС некоторому виду формируемой деятельности (навыкам алгоритмической природы) [2-8].Указанные инструментальные средства использовались при проектировании ИОС грамматикам естественных языков (немецкого и русского). Использование бейесовского подхода при идентификации (оценке) навыков/умений обучаемого и осуществление прогнозирования состояния обученности обеспечивают учет предыстории обучения, что является основой для организации адаптивного обучения.