Модель управления скоростью вытягивания монокристаллов кремния

Управление скоростью вытягивания кристаллов полупроводниковых материалов, выращиваемых из расплава по способу Чохральского, заключается в следующем: во вращающемся вокруг своей оси с угловой скоростью W _т тигле с внутренним диаметром D находится жидкий расплавленный металл (рис. 1); кристалл диаметром d вытягивается из расплава со скоростью вытягивания V з и угловой скоростью вращения W з ; процесс проводится в камере, наполненной инертным газом аргоном. Общий вид микропроцессорной установки вытягивания кристаллов кремния приведен на рис. 2.

Температура расплава формируется за счет управления мощностью нагревателя на основе показаний датчика температуры T _з боковой поверхности нагревателя. Управление скоростью вытягивания кристаллов кремния по программе позволяет сформировать плоский фронт кристаллизации при выращивании прямого конуса, цилиндрической части и обратного конуса кристалла, что необходимо для многих марок кристалла и обеспечивает минимум дислокаций, т. е. нарушений монокристаллической структуры в выращенном монокристалле. Отклонение от цилиндрической формы по длине кристалла повышает вероятность образования дислокаций в местах перегиба формы, за счет повышенных механических напряжений в них, возникающих в процессе охлаждения кристалла.

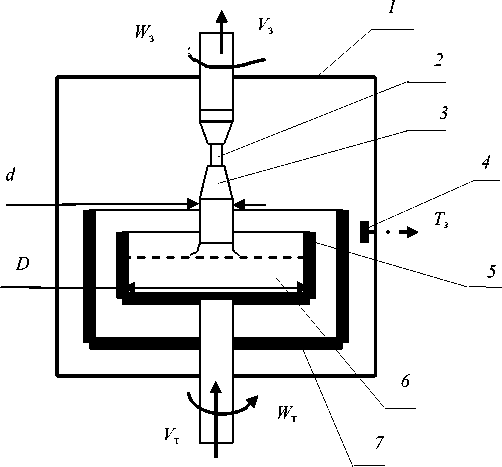
Рис. 1. Схема выращивания кристаллов кремния:

1 - камера; 2 - затравка; 3 - кристалл; 4 - датчик температуры; 5 - тигель; 6 - расплав металла; 7 - нагреватель

По данным многих исследователей [1–4], обеспечение условий получения плоского фронта кристаллизации при выращивании кристаллов кремния и германия (с необходимой величиной осевого градиен- та температур в выращиваемом кристалле) позволяет получать кристаллы с совершенной структурой (минимумом дислокаций).

Рис. 2. Общий вид микропроцессорной установки вытягивания кристаллов кремния

Превышение скорости вытягивания кристалла кремния некоторой пороговой величины приводит к прогибу фронта кристалла вверх и отрыву фронта кристаллизации кристалла от расплава, т. е. к срыву процесса монокристаллического роста. Уменьшение скорости ниже другой пороговой величины приводит к опусканию фронта кристаллизации кристалла вниз и касанию твердой фазы фронта кристаллизации дна тигля, что ведет к поломке технологической оснастки и аварийной остановке процесса. Поэтому в практике выращивания монокристаллов кремния актуальной является проблема разработки математического аппарата для задания скорости вытягивания кристалла, исходя из условия плоского фронта кристаллизации. Для получения монокристаллов кремния высокого качества необходимо обеспечить форму фронта кристаллизации, близкую к плоской на участках выращивания прямого конуса, цилиндрической части и обратного конуса кристалла, что дает возможность получить одновременный устойчивый монокристаллический рост. Ниже приведены математические выражения для формирования закона изменения скорости вытягивания V з ( x ), которые позволяют автоматизировать процесс ввода этого параметра в систему управления установкой. Модель управления скоростью вытягивания (рис. 3) монокристалла кремния можно представить в виде выражения

V(x) = F(Z, Y, X, L(x), x), где X - величина среднего перегрева расплава; x - координата перемещения вдоль оси кристалла; L(x) – линейный осевой градиент в твердом кристалле; Z – вектор задания геометрии выращиваемого кристалла; Y – вектор задания теплофизических параметров материала.

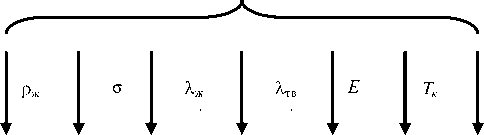
Математическую зависимость величины среднего перегрева расплава λ относительно температуры кристаллизации материала [3; 4] можно представить виде следующего выражения:

X = C, ■

E где C V =Р ж v^;

^X тв

( L — C v ■ V з )

x = ( т - T ) ;

d c =4. C'Xтв • ,                                            ;

р_ж-X ■ g жж

Vз – скорость вытягивания кристалла; Τк – температура кристаллизации материала; Τ – температура расплава в зоне фронта кристаллизации; L – линейный осевой градиент в твердом кристалле; E – удельная теплота плавления материала; Хж - коэффициент теплопроводности расплава; Хтв - коэффициент теплопроводности кристалла; g – ускорение свободного падения; d - диаметр кристалла; о - поверхностное на- тяжение расплава.

В общем случае средний перегрев λ есть функция осевого градиента в кристалле L и скорости вытягивания кристалла V з . Процесс управления основными параметрами выращивания кристалла показан на рис. 4.

Используя линейную аппроксимацию параметров на узловых участках выращивания кристалла, получены выражения для определения задания скорости вытягивания Vз(x) на конусной, цилиндрической части кристалла и при формировании обратного конуса со- ответственно:

V з ( x ) = V 0

^x ■^{[ V} 0 - ^V ] .

x ₁

V ₃( x ) = V 1

(x-x 1 )-[v -V2], (x2 - xi)      ’

V , ( x ) = V 2 +

⁽ x ^- x 2 ^)- [ ^V 3 - ^V 2 ] ( ^x 3 ^{- x} 2 )

где V 0 - начальная скорость вытягивания кристалла; V 1 - скорость вытягивания кристалла при завершении формирования обратного конуса; V 2 - скорость вытягивания кристалла при завершении формирования цилиндра; V ₃ - скорость вытягивания кристалла при завершении формирования обратного конуса; x 1 - координата завершения формирования прямого конуса кристалла; x ₂ - координата завершения формирования цилиндрической части кристалла; x ₃ - координата завершения формирования обратного конуса кристалла;

x - координата перемещения вдоль оси кристалла.

Для автоматического определения значений координат скорости вытягивания в узловых точках ( V ₀, V ₁, V ₂, V ₃) преобразуем выражение (1) к виду выражения (5), введя технологические поправочные коэффициенты β i :

V 3 ( d ) =

L -

X- d₃ C t

Р, ■------------- ,

V

где V ₃( d ) - скорость вытягивания кристалла; d ₃ - задание диаметра кристалла на прямом конусе, цилиндрической части и обратном конусе; в , - технологический коэффициент снижения скорости (0,9…0,7).

Y

рт

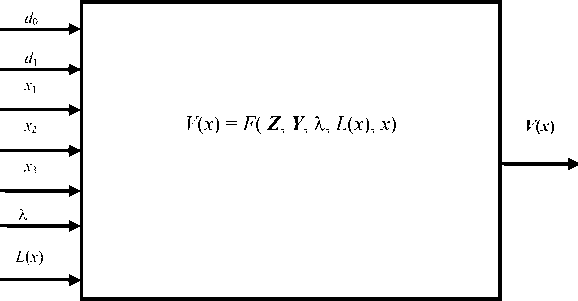
Рис. 3. Модель управления скоростью вытягивания монокристалла кремния

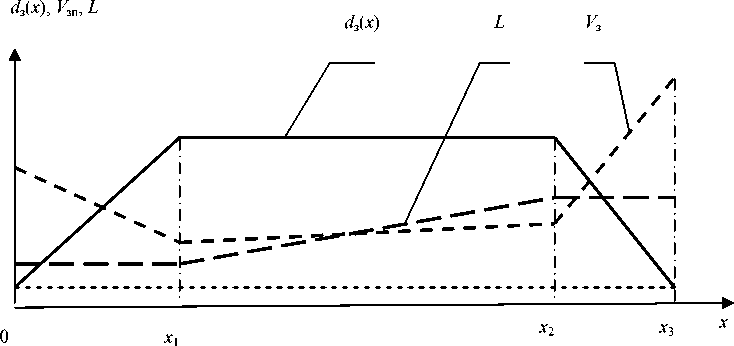
Рис. 4. Задание параметров процесса выращивания кристаллов:

d з ( x ) - задание диаметра; V , - задание скорости вытягивания; L - задание осевого градиента; x - перемещение вдоль оси кристалла

Из (5) для узловых точек скорости вытягивания получим выражения:

V о = L о

—

X- d 0

C t

Р о .

•------------- с

V

V = L 0

!• d 1 '0 - ^

V 2 = L

—

X- d 1

C t

V 3 = L i

—

Р1. •------------- с V

•

С

V

X- d 0

C t

Рз •------------- ,

V

где L о - осевой градиент в начале цилиндрической части кристалла; L i - осевой градиент в конце цилиндрической части кристалла; V 0 , V 1 , V 2 , V 3 – узловые точки скорости вытягивания; d 0 - диаметр вытягиваемой шейки кристалла; d 1 - диаметр цилиндрической части кристалла.

Технологические поправочные коэффициенты β i введены для корректировки скорости вытягивания, исходя из технологических требований (например, равномерности легирования кристалла по его длине, при допущении некоторой величины прогиба фронта кристаллизации). Осевой градиент в выращиваемом кристалле кремния можно рассчитать на основе непрерывного измерения температуры пирометром в области выращивания на боковой поверхности кри-

сталла (на расстоянии 8…10 мм от расплава) в процессе роста, при этом пирометр устанавливается на смотровое окно камеры установки вытягивания. Другим способом определения осевого градиента в выращиваемом кристалле является метод непрерывного измерения температуры термопарами (введенными в камеру установки), вблизи боковой поверхности выращиваемого кристалла. Применяя микропроцессорные системы управления выращиванием кристаллов кремния, вычисление осевого градиента можно автоматизировать. На основе выражений (1)–(9), c подстановкой в них физических постоянных полупроводникового материала кремния [5], на рис. 5 и 6 при- веден пример моделирования задания диаметра кристалла кремния и его скорости вытягивания на всех участках.

Моделирование скоростей вытягивания кристаллов кремния и германия [4] показало, что рабочий диапазон скорости вытягивания германия (0,2…1 мм/мин) и кремния (2…10 мм/мин) отличается на порядок, что согласуется с теплофизическими параметрами данных материалов. Основной трудностью для применения данной модели при выращивании монокристаллов кремния является практическое измерение и вычисление осевых градиентов при выращивании новых марок кристаллов.

d з ( x ), см

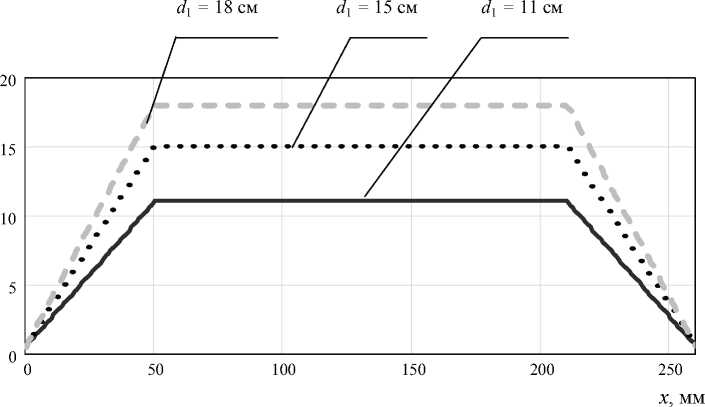
Рис. 5. Задание диаметра кристалла кремния: при x ₁ = 50 мм; x ₂ = 210 мм; x ₃ = 260 мм; d ₀ = 0,5 см

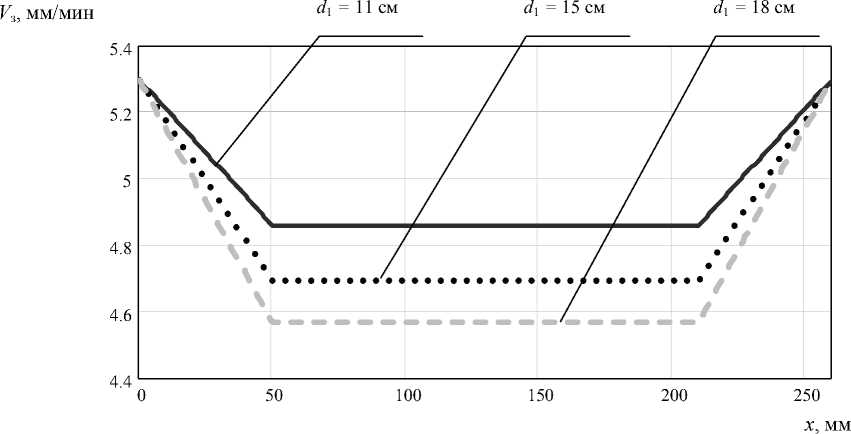
Рис. 6. Задание скорости вытягивания кристалла кремния: при λ= 0,2 ^оС; L ₀ = 15 ^оС/см;

L 1 = 15 ^оС/см; β 1 = β 2 = β 3 = β 4 = 0,8; d 0 = 0,5 см; x 1 = 50 мм; x 2 = 210 мм; x 3 = 260 мм; d 0 = 0,5 см

Итак, предложена математическая модель формирования скорости вытягивания монокристаллов кремния, выращиваемых по способу Чохральского. Это позволяет автоматизировать процесс ввода параметра скорости в систему управления и сокращает цикл производства готовой продукции требуемого качества, обеспечивая при выращивании кристалла форму фронта кристаллизации, близкую к плоской.