Модель вибратора для проектирования вибромашин

Одним из направлений развития машиностроения является проектирование и производство вибромашин, начиная от низкочастотных дорожных виброкатков и виброплит для трамбовки дорожного полотна и укладки асфальта и завершая высокочастотными компактерами для создания новых материалов и установками для литья металлов под давлением. Одной из проблем при проектировании таких вибромашин является выбор параметров вибрации рабочего инструмента, значения которых должны зависеть от размера частиц обрабатываемого материала. Общеизвестно, что при укладке дорожного полотна с применением виброплит используют частоты около 30 Гц, что обеспечивает резонансные колебания частиц грунта диаметром примерно 40 мм, при этом окружающие их более мелкие частицы не перемещаются и взаимодействие крупных частиц между собой не происходит. Спасти ситуацию позволяет присутствующее здесь ударное воздействие виброплиты на грунт в сочетании со статическим пригрузом и использование более высоких кратных частот – 60 и 90 Гц, что обеспечивает подвижность не только крупных частиц, но и частиц размером 10…20 мм.

Аналогичная ситуация наблюдается и в области производства высокочастотных устройств. Например, в последние годы идут разработки новых технологий компактирования нанопорошков [1], размеры частиц которых лежат в диапазоне 1…100 нм. Основная задача – обеспечить равномерное распределение плотности нанопорошка в компактах разной формы, сохранить нанострук- туру в прессовках для формирования наноразмерных зерен в процессе спекания, т. е. создать условия для подавления роста зерен и спекания тем самым нанокристаллических изделий с заданными функциональными свойствами. Для решения этой задачи чаще всего используют полуволновые концентраторы [2] на одной из стандартных ультразвуковых частот (21, 27… 44 кГц), используя уже другой критерий – размер наночастицы должен быть соизмерим с амплитудой колебаний рабочего инструмента [2]. Аналогичный результат можно было бы получить при наложении на матрицу ударных воздействий, так как их спектр частот обычно не превышает вышеуказанный диапазон низкочастотного ультразвука. Такой подход не всегда эффективен.

Исходя из размера наночастиц, для создания их подвижности в процессе компактирования требуется уже радиочастотный диапазон ультразвукового воздействия большой мощности, например радиоимпульсы с высокочастотным заполнением [3]. Здесь необходимо искать самые современные технические решения, обеспечивающие максимальную величину электромеханической связи и КПД вибропреобразователей. Например, дополнительные возможности для изменения характеристик высокочастотных преобразователей дает использование в них двух и более пьезоэлементов [4–7], при этом уже разработаны двухэлементные двухчастотные преобразователи, позволяющие существенно улучшить эксплуатационные характеристики при расположении пьезоэлементов соосно [8] или концентрично [9]. Также показано, что создание акустического резонанса между двумя излучающими элементами с переменным зазором между ними позволяет увеличить интенсивность возбуждаемого акустического поля на 12 дБ и обеспечить перестройку частоты до 24 % относительно резонансной [10], что обеспечивает подвижность частиц с нестабильными размерами в уплотняемом компакте.

Отметим, что аналогичные методы воздействия можно использовать и при литье изделий сложной формы, однако основным фактором воздействия на жидкий металл здесь уже является косвенное явление – ультразвуковая кавитация – микровзрывы пузырьков газа с масштабом явления от одного до нескольких десятков микрон, который соизмерим с размером зерен, зарождающихся при охлаждении слитка [11]. Это способствует их подвижности и образованию мелкого равновесного зерна, повышению однородности слитка и уменьшению степени развития «ликва-ционных» процессов, что, в конечном итоге, приводит к существенному улучшению потребительских свойств литого изделия.

Как видим, утилитарная, казалось бы, задача превращается в разработку с большим количеством экспериментальных исследований. При этом разработчики не уделяют в нужной мере внимание выбору оборудования с необходимой частотой вибрационного воздействия, при том что частота является важнейшим параметром наряду с амплитудой колебаний инструмента. Одна из причин – это отсутствие на рынке должных предложений. Очевидно также, что нужен системный подход в конструировании такого типа устройств на произвольную частоту и первое с чего, на наш взгляд, надо начать – это разработка моделей мощных вибраторов, унифицированных для работы в широком диапазоне частот (1... 100 кГц).

В работе рассматривается конструкция и модель универсального вибратора, пригодного для использования в широком диапазоне частот, принцип действия которого основан на изгибных поперечных колебаниях пластин. В отличие от полуволновых преобразователей стержневого типа данная конструкция при меньших габаритных размерах и энергопотреблении обладает в вышеуказанном диапазоне частот большим динамическим диапазоном колебаний рабочего инструмента, форму рабочей поверхности которого можно задавать произвольной. Разработанная математическая модель применима как для низкочастотных, так и высокочастотных преобразователей, так как выполнена с использованием безразмерных комплексов теории подобия. Модель учитывает упругий гистерезис элементов конструкции, обеспечивая тем самым достоверные величины амплитуды резонансных колебаний рабочего инструмента.

Модель вибратора

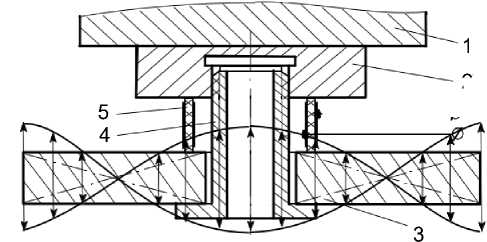
Вибратор представляет собой электромеханический комбинированный преобразователь, в котором пьезокерамический цилиндр 5 (рис. 1, а) сопряжен с одной стороны с упругим высокодобротным элементом 3 (пластина), а с другой – инерционным концевым элементом (концевик) 2, являющимся рабочим инструментом для воздействия на нагрузку 1, например на одну из стенок матрицы для прессования или сам является этой стенкой. Полая или цельная шпилька 4 связывает конструкцию в единое целое и позволяет также задать необходимую величину предвари- тельного напряжения сжатия, что улучшает как прочностные характеристики конструкции, так и действие пьезоэффекта [12]. Пьезокерамический цилиндр 5 связан с внешним источником переменной частоты и реализует обратный пьезоэффект.

Влияние нагрузки 1 может проявляться различно. При небольших габаритах жесткой нагрузки 1 ее влияние можно учесть, как дополнительную массу к массе концевика 2, однако, в общем случае, когда характерные размеры поверхности излучения сравнимы с длиной волны в нагрузке (сыпучая среда или жидкость), влияние нагрузки следует рассматривать как комплексную величину [13]. В любом случае учет влияния нагрузки на вибрирующий объект – это нетривиальная задача, связанная иногда с решением интегральных или дифференциальных уравнений в частных производных, например, в виде упругогидродинамической задачи.

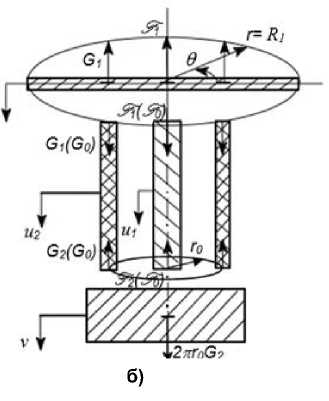
Математическая модель. Для описания изгибных поперечных колебаний круглой пластины используем моментную теорию оболочек [14]. Продольные колебания пьезокерамических стержней и цилиндров описываем с помощью одномерного волнового уравнения [15]. Учтем также, что абсолютные значения упругих постоянных пьезокерамики зависят от условий на электрической стороне, поэтому принимаем, что модуль Юнга E ^e и другие определены при постоянной напряженности e электрического поля [13], что характерно для работы преобразователя в режиме излучения. В модели действие пьезоэффекта со стороны цилиндра заменяем парой противоположно направленных интенсивностей G о , приложенных по окружности на краях цилиндра (рис. 1, б). В случаях, когда шпилька 4 также наделена пьезоактивными свойствами (пьезостержень), необходимо добавочно рассматривать пару противоположно направленных сил F 0 (рис. 1, б), приложенных в полюсе пластины в направлении согласованном с направлением G о и с реализуемой формой колебаний.

W

■0

а)

Рис. 1. Вибратор (a) и его расчетная модель (б)

Свяжем неподвижную систему отсчета со срединной плоскостью пластины и направим осевую координату вдоль продольной оси симметрии как это показано на рис. 1, б. Поперечные колебания пластины w будем рассматривать в полярной системе координат ( г, 9 ). Обозначим перемещения элементов вибратора относительно неподвижной системы координат следующим образом: продольное относительное перемещение стержня - и 1 , пьезоэлемента - и 2 , инерционной массы - v . Разобьем сенсор на составляющие, заменив связи их реакциями, и воспользуемся методом кинетостатики для записи уравнений движения. Колебания пластины [14, 15] опишем следующим уравнением:

D 0 A r 9 A r 9 w + p h —T = Ф ( r , 9, т ), ^,       ,                d t

Используем условия свободного края [14] на граничном контуре при r = R i и ненулевые начальные условия. В выражении (1) введены обозначения: A г, 9 — оператор Лапласа; Ф ( г, 9, т ) - функция поперечных возмущений на пластину; D о = Eh ³ /[12(1-ст)] - цилиндрическая жесткость; р, E, ст - плотность, модуль Юнга и коэффициент Пуассона материала пластины; h - толщина пластины.

Определим вид функции Ф ( г, 9, т) и воспользуемся для этого понятием стандартизующей функции [16], что позволяет нам получить задачу с нулевыми значениями краевых и начальных условий:

Ф ( r , 9 , t ) = G_x 5 ( r - r ) - F _x 5 ( r ) + p h - [ w ( r , 9 ) ^ ( t ) + w ‘ ( r , 9 ) 5 ( t )]. (2)

Здесь G 1 – интенсивность реакции связи со стороны пьезоэлемента, распределенная по окружности радиуса r = r о (Ar о - толщина элемента); F i - сосредоточенная реакция связи со стороны стержня, приложенная в полюсе пластины; 5, 5' - дельта функция и её первая производная по соответствующей координате, которая в силу своей избирательности указывает на место и время приложения воздействия, например, начальных условий w i ( r,9) и w' 2 ( r,9).

Введем в рассмотрение следующие безразмерные параметры: w = w / h 0 , u 1 = u 1 / h 0 , u 2 = u 2 / h 0 , v = v/h о , т =to o t, to* = ю/to o , n = x/l 2 (1 i =1 2 ) , 8 k о r , k о ph так/D о , где to o и h о - характерная частота и амплитуда колебаний, P о - атмосферное давление. При решении колебательной задачи ( t ^да ) можно не учитывать влияние начальных условий и ограничиться рассмотрением используемых чаще всего на практике осесимметричных форм колебаний, что позволяет записать полную систему уравнений движения вибратора в следующем виде:

fi 2w                         *1 A , A ^ w + -т = - G 1 - Bv 5 ( 8 -^ o) to 2 - F 1 - B 2 5 ( 8 ) / ( 8 - to ), fir fi2 w     ( 1 d 2 w )!           Г d (    \1 —x + с т--у     = 0,   — A, w     = 0, 2        2                             8 L 8     <  8 8 7J / 8= R       L 8       J / 8= R , d u 1 = k , d^ uL ,   d u l    = b i ( F 1 + F o A i ), d u l    =- b i ( F 2 + F o » ; ), 5т        8p      8p / n = o                      8p / n = 1 1 apu^ = fc 2 | 2 u 2 ,   d u^    = 6 1 ( 0 1 + g o д 2 ),   au^   =- ь ^ ( g 2 + g o a 2 ), дт         Sn      Sn / n = o                         dn / n = Z | d - v = A o (4 n G 2 + F 2 + P ); а т U 1 (0) = w(0), U 2 (0) = w(8 o ), U 1 (1) = U 2 (1) = v .

(3) (4) (5) (6) (7) (8)

В этих уравнениях введены следующие обозначения:

B i =P о 2nR i /(D о к о³ h о ), B 2 = P о R i² /(2D о к о² h о ), P =P/ P о , G 1 = G i /(P о 2nR i ),

G2=G2/(Pо 2nRi), F 1=Fi/(PoпRi2), F2=F2/(PoпRi2), кi=tooli/ci, к2=tooli/c2, bi= PoпRi2li2/(EiSihо),                                                                (9)

b2=Pо^il2/(EieArоhо), R1=k0Ri, Xo= PonRi2/(motoo2ho), а символ Кронекера Aj (i = 1,2) указывает на воздействие Fо со стороны шпильки (j = i) или цилиндра G0 (j = 2); c1 и c2 – скорости звука в продольном направлении стержня и цилиндра.

Допускаем, что рассеивание энергии при колебаниях равномерно размазано по объему материала, зависит от амплитуды деформации и не зависит от частоты [17, 18]. Связь между амплитудами напряжений т о и деформаций A x о описывается петлей гистерезиса и может быть представлена в следующим виде [17]:

т о = E-Ax o (1+jA v/2n), (i о) где A ^ - эквивалентный коэффициент поглощения энергии, j - мнимая единица, E - модуль упругости материала элементов сенсора. Зависимость (10) предполагает решение задачи (3) – (8) на комплексной плоскости.

Функция Грина вибрирующей круговой пластинки. Для решения смешанной краевой задачи (3…8) воспользуемся методом функции Грина, который позволяет свести решение задачи к интегральному виду (в свертках). Как известно, фундаментальное решение линейного дифференциального уравнения в теории обобщенных функций совпадает с обобщенной функцией Грина G [19]:

6 6 6 х „

L (’    ’   ) G ( 5 , a ; 0 , _Ф ; т , и ) = 6 ( 5 , 0 , т ),

∂ξ ∂θ ∂τ где L – линейный дифференциальный оператор. Учтем синусоидальные смещения пластины во времени и разложим дельта функцию в тригонометрический ряд по θ (рис. 1, б):

∞

6(5,0,т) = - 6(5) exp((шт) £ (1 - 0,5 Am) cos(m0),

П где Δ0m – символ Кронекера. Представим искомую функцию Грина аналогичным рядом

∞

Gg (5, а,0,т) = exp(ito т)£ Gm (5, a )cos(m0).(13)

m = 0

Подставляя выражение (13) и тригонометрический ряд (12) в уравнение (11), получим в общем виде решение

G m ( 5 , a ) = (1 - 0,5 A m ) L 6- a ), (14) которое включает в себя [19, 20] сингулярную часть G m+ ( ξ,α ) и аналитическую часть G m 0 ( ξ,α ). Функция G m0 должна удовлетворять однородному уравнению, соответствующему уравнению (11). Общее решение однородного уравнения имеет вид [20] линейной комбинации функций Бесселя:

G m 0 ( 5 ) = C m J ( 5 ) + C 3 m Y ( 5 ) + C 2 Jm ( 5 ) + C 4 m K m ( 5 ),                                              (15)

где C 1 m … C 4 m – произвольные постоянные. Сингулярную часть решения определяем в виде:

G m ₊ ( 5 , a ) = H 0 ( 5 - a ) G m 0 ( 5 ),                                                              (16)

где H 0 ( ξ–α ) – функция Хевисайда. Функция G m+ ( ξ,α ) должна удовлетворять уравнению с правой частью L m G m+ =δ и, следовательно, можно удовлетворить этому уравнению, используя неизвестные нам постоянные в выражении функции G m 0 ( ξ,α ). Дифференцируя выражение (15) в пространстве обобщенных функций, приходим к системе алгебраических уравнений линейной относительно искомых постоянных С 1 … С 4 , решение которой можем получить аналитически. Подставляя найденные коэффициенты в выражение (14), находим функцию Грина пластины. Ограничимся опять рассмотрением осесимметричных форм колебаний, что позволяет проинтегрировать полученное выражение по θ от нуля до 2 π :

G ( 5 , a ) exp( i to т ) =    • { H 0 ( 5 - a )[ Y ( a ) J ₀ ( 5 ) - J 0 ( a ) Y ( 5 ) + ^- K 0 ( a ) 1 0 ( 5 ) -

4                                 n

• 2    „  , _ „   „ „  „ „  „ „   , „   , . .

• -    -1 0 ( a ) K 0 ( 5 )] + C 10 J 0 ( 5 ) + C 30 Y 0 ( 5 ) + C 20 1 0 ( 5 ) + c 40 K 0 ( 5 )} exp( j to т ).

π

Произвольные постоянные C 10 … C 40 определяем из условий регулярности решения в полюсе и из краевых условий (4). В частности, учитывая, что Y 0 ( ξ ) →∞ , K 0 ( ξ ) →∞ ( ξ → 0), получаем C 30 = 0 и C 40 = 0. Значения постоянных C 10 и С 20 определяем из условий свободного края (4). В результате получаем искомую функцию:

G ( 5 , a ) exp( ito т ) = -- • { H ₀ ( 5 - a )[ Y 0 ( a ) J ₀ ( 5 ) - J ₀ ( a ) Y 0 ( 5 ) + - K 0 ( a ) 1 0 ( 5 ) -

- -1 0 ( a ) K 0 ( 5 )] - Y 0 ( a ) J 0 ( 5 ) - - K 0 ( a ) Y , ( 5 ) + ππ

4C„                 4C.„2

+ (—10 + Y0 (a))J0 (5) + (—21 + - K0 (a))10 (5)} exp(jto т). πα           παπ

Импульсная функция вибратора. Для определения импульсной функции (Грина) всего вибратора необходимо определить неизвестные реакции связей G 1, G 2 и F 1, F 2 (см. рис. 1, б). Общий вид решения уравнений (5) и (6) для амплитуд колебаний ищем в виде:

U10 = Aicos(kito*n)+ Bicos(kito*n),

U 20 = A 2 cos( k 2 to*n )+ B 2 cos( k 2 to*n ),

где А 1 ... В 2 - произвольные постоянные. Подставим выражения (19) в краевые условия (5) и (6) и найдем значения постоянных А 1 ... В 2 . Далее, используя условия сопряжения по перемещениям элементов сенсора, можем найти выражения для неизвестных реакций связей. В частности

Fi=kto* wol(0)cos(kto^) - vo)/bisin(kito*)] - FoAii(20)

G2=\k 2 to*svn(k 2 to * )/b 2 ] W o (^+k 2 to*cos(k 2 to * )-\w o ( o )cos(k 2 to * )-v o ]/bsinfato * - G o ^ 2 ⁱ.

Подставляя найденные реакции F 2 и G 2 в выражение (7), можно найти амплитуду колебаний концевика 2 (рис. 1, а):

vo= [FoXoAii^4nG)XoA2i- Wo(0)X^^ito*/sm(kito*)-Wo(^)4nX^^2to*/(21)

/sin( k 2 ω^* )]/[ ω^*2– λ 0 Ω 1 ω^*ctg(k 1 ω^*) – 4 π λ 0 Ω 2 ω^*ctg(k 2 ω^* )].

Выражение для стандартизующей функции (2) принимает вид:

Ф(О = G1-5(^-^o) - Fi-S(^) = {k2to*[wo(^o)cos(k2to‘)-vo)/b2sin(k2to')]-(22)

–G 0 Δ 2 ⁱ)} ⋅ δ(ξ –ξ 0 ) – {k 1 ω^* [ w 0 (0)cos( k 1 ω^* ) – v 0 )/ b 1 sin( k 1 ω^* )] – F 0 Δ 1 ⁱ)}δ(ξ).

Воспользуемся функцией Грина (18) и выражениями (21) и (22) для построения структурной схемы [16] вибратора, показанной на рис. 2. На схеме введены следующие обозначения:

Ω 1 = k 1 /b 1 , Ω 2 = k 2 /b 2 , B 31 = λ 0 Ω 1 , B 32 = λ 0 Ω 2 ,

W 1 = B 31 ω^*/sin ( k 1 ω^* ),

W 2 = 4 πB 31 ω^*/sin ( k 2 ω^* ),

W 3 = [to*² - B 3i to*ctg(k i to*) - 4 п B 32 to*ctg(k 2 to * )Yⁱ,                                            (23)

W 4 = Ω 1 ω^*/sin(k 1 ω^*),

W 5 = Ω 2 ω^*/cos(k 2 ω^*),

W 6 = Ω 1 ω^*ctg(k 1 ω^*),

W 7 = Ω 2 ω^*ctg(k 2 ω^*).

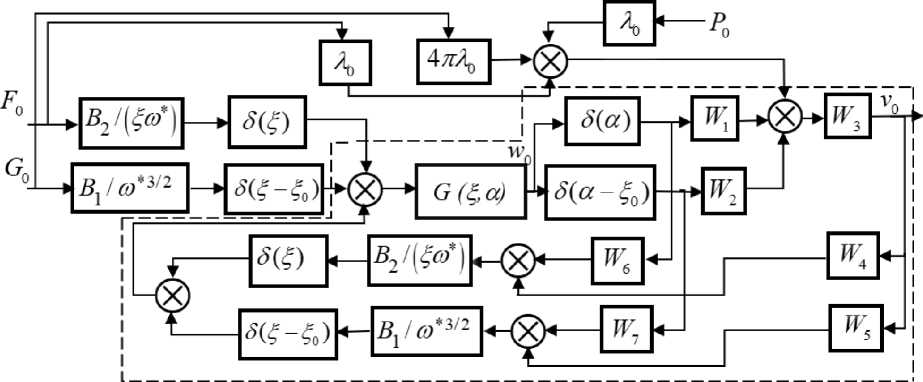
Рис. 2. Структурная схема вибратора

Особенностью структурной схемы является использование дельта-функций 3(£) для указания мест отбора и наложения воздействий в распределенном объекте. Видим, что функция Грина пластины G(£0) охвачена четырьмя контурами «вырожденной» [16] обратной связи, которые алгебраически преобразуются в эквивалентную импульсную функцию О(£а) (на схеме она обведена пунктирной линией), учитывающую взаимовлияние всех элементов вибратора. Влияние нагрузки на вибратор описывается здесь амплитудой Pо некоторого распределенного по площади безразмерного давления P, являющегося следствием вибрации и действующего в силу резонансных (фильтрующих) свойств вибратора синхронно даже при существенно нелинейной нагрузке, при этом ее комплексный характер учитывается наличием в величине P0 синфазной и квадратур- ной составляющих давления. В результате амплитуда колебаний рабочего инструмента определяется выражением:

V 0 = F 0 X 0 N 1' W 3 +4nG a X o ^ 2 W 3 - W 0 (0 W i W 3 - W )( & ) W 2 W 3 + P 0 X 0 W 3 ,                   (24)

где выражение для распределения амплитуд прогиба пластины имеет уже алгебраическую форму в силу фильтрующих свойств дельта-функции:

w o (;) = {(F 0 N 1 +P 0 )B ₂[ X 0 W 3 W , + 1/(^o * )]5(G) +G a B i X o N 2 (4nW 3 W 7 +1/to * ³ /2 8(^- 0 +   (25)

+ 4 n G a N 2 B 1 X 0 W 3 W 4 §(G) + (У0М+Р 0 JX 0 W 3 W 7 §(^ - ^ a )} ® G( ^,a ).

Учет неупругого сопротивления по формуле (10) приводит нас к необходимости замены b 1 , b 2 и k на их комплексные аналоги:

b i* = b i /(1+ jNy/2n), b 2 = b 2 /(1+ jNУ/2П), k= k 0 (1+ jN^/2n) V^ k 0 (1 - jNy/8n) (26)

Решение общей задачи связано с дискретизацией и вычислением комплексных алгебраических выражений (24) и (25), которые можно выполнить в любой специализированной вычислительной системе.

Численное исследование и валидация модели

Рассмотрим некоторые результаты расчетов. Исходные параметры численной модели сенсора повторяют параметры натурной модели: масса концевого элемента – 850 г , масса стержня – 20 г , масса пластины – 1500 г , внешний и внутренний диаметр пластины R 1 = 120 мм и R 2 = 22 мм, толщина пластины h = 15 мм, диаметр концевого элемента – 64 мм, толщина концевого элемента – 12 мм, длина стержня и цилиндра – 10 мм. Внешний диаметр и толщина стенок цилиндра – 26 мм и 1,65 мм. Материал металлических элементов – инструментальная сталь, пьезокерамика – ЦТС-844.

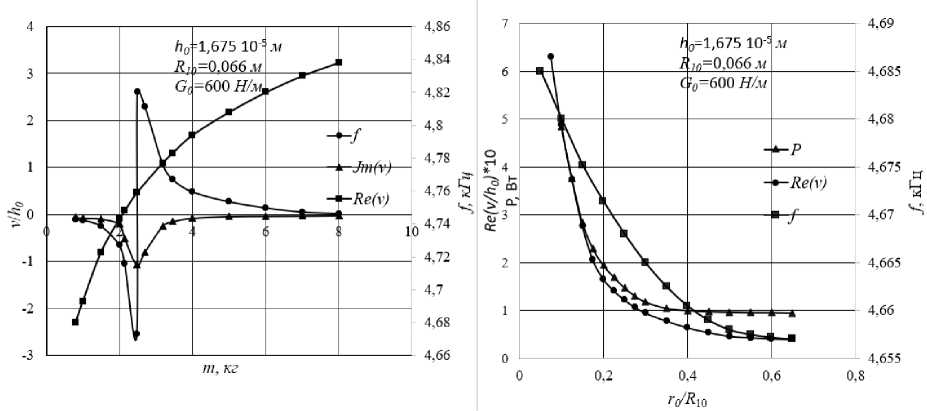
На рис. 3, а представлены расчетные зависимости безразмерной амплитуды колебаний активной поверхности от величины массы концевого элемента (резонансные значения) и кривая изменения резонансной частоты. Видим, что с изменением массы в представленном диапазоне резонансных частот к основному резонансу, связанному с колебаниями пластины, присоединяется еще одно резонансное явление, связанное с колебаниями стержня или цилиндра с массой на конце. Такие резонансы обычно происходят не на собственных (парциальных) частотах элементов конструкции, а на комбинационных частотах, функционально связанных с собственными. Исследовалось также влияние диаметра пьезокерамического цилиндра на амплитудно-частотные характеристики вибратора (рис. 3, б). Увеличение диаметра пьезоцилиндра вызывает уменьшение амплитуды резонансных колебаний на поверхности концевого элемента и пластины.

а)                                                          б)

Рис. 3. Резонансные характеристики вибратора в зависимости от массы концевого элемента (а) и радиуса пьезокерамического цилиндра (б)

Валидация модели по натурному образцу показала высокою точность определения резонансных частот и форм колебаний пластины в составе вибратора. Относительная погрешность расчета пя- ти нижних резонансных частот вибратора для вышеуказанных параметров менее 0,05 %. Для учета конструкционного и внутреннего трения требуется «калибровка» модели на ее натурной копии в резонансном режиме (использовались пьезопленочные датчики SDT1 фирмы Measurement Specialties, наклеенные узкой полосой по радиусу пластинки для захвата зоны узла и смежной с ним зоны пучности колебаний). После такой «калибровки» и определения эквивалентного коэффициента поглощения Δψ в формуле (10) точность расчета амплитуд колебаний на данной модели сенсора ограничена в основном инструментальными погрешностями измерительного оборудования, модельными допущениями и погрешностью аппроксимации дискретной модели: относительная погрешность расчета резонансных амплитуд колебаний менее 1 %, а для нерезонансных значений амплитуд – менее 0,2 %.

Выводы

Данная модель может использоваться как основа для проектирования вибромашин различного типа, принцип действия которых основан на изгибных колебаниях упругих элементов. Она позволяет удовлетворить требованиям по частоте и амплитуде колебаний рабочего инструмента при возможных ограничениях на габариты и массу, решив тем самым задачу синтеза и другие оптимизационные задачи. Мы ограничили благоприятный выбор рабочих частот диапазоном 1…100 кГц, но это не значит, что конструкция не реализуема для частот порядка сотни герц или выше 100 кГц, учитывая, что оборудование и технология изготовления могут существенно измениться. В мегагерцовом диапазоне частот предпочтение надо отдать полуволновым преобразователям.

Модель учитывает упругий гистерезис, а использование безразмерных комплексов позволяет распространить полученное решение на подобные объекты. Решение колебательной задачи в свертках определяет ее «вырожденное» (24, 25) решение в алгебраической форме, что существенно упрощает модель и делает ее пригодной для инженерных расчетов.