Модель возбужденного состояния и дырочная теория жидкостей и стекол

В настоящее время в физике конденсированного состояния более или менее подробно исследованы кристаллы. Что касается природы аморфных твердых тел, чаще называемых некристаллическими твердыми телами (non-crystalline solids), располагаем весьма скромной информацией. Дифракционные и другие структурные методы, успешно применяемые для кристаллов, оказываются малоэффективными для этих систем. Вместе с тем некристаллические материалы, например, полимерные и другие стекла, находят широкое применение на практике. Появляются новые аморфные твердые тела, в частности металлические стекла (аморфные сплавы), которые получают сверхбыстрым охлаждением расплавов металлов [1-6].

Примерно такая же ситуация наблюдается и в области исследований жидкого состояния вещества, которое занимает промежуточное положение между твердым и газообразным состояниями. Если в течение длительного времени жидкости рассматривали как сильно сжатые газы, то открытие ближнего порядка в них дало качественно новую основу для построения теории жидкого состояния. Предложены различные варианты твердотельных моделей жидкостей [1, 2, 6-9].

Наряду с приближенными подходами идет развитие строгих физических теорий, основанных на методах статистической физики. Однако на этом пути, по существу, пройден лишь начальный этап. Строгий расчет термодинамических функций аморфных сред встречает серьезные математические трудности. Такие расчеты удалось выполнить лишь для простейших систем типа жидкого аргона [1, 11]. Поэтому на данном этапе по-прежнему актуальны разработки модельных представлений о жидкостях и аморфных твердых телах. Среди них широкое распространение получила дырочная модель (концепция свободного объема). При этом природа свободного объема и дырок в аморфных средах остается во многом не ясной [1, 5-12].

В настоящей работе на основе развития модели возбужденного состояния [13-15] предлагается новый подход к интерпретации механизма образования флуктуационной дырки в жидкостях и стеклах. Развивается представление о том, что флуктуационный свободный объем аморфных сред, по сути дела, не является собственно свободным объемом в традиционном понимании по Ван-дер-Ваальсу и его целесообразно называть просто «флуктуационным объемом» без прилагательного «свободный». В связи с этим рассмотрены некоторые аспекты модели возбужденного состояния. Если основное уравнение данной модели ранее было получено из газовой модели, то здесь показано, что можно вывести его из общих принципов статфизики без привлечения модели газа.

Основные положения модели возбужденного состояния

Элементарным актом многих молекулярно-кинетических процессов в жидкостях и аморфных средах служит предельная упругая деформация межатомной или межмолекулярной связи Δr_m , соответствующая максимуму квазиупругой силы. Такой элементарный акт можно интерпретировать по другому как смещение кинетической единицы на критическое расстояние Δr m , соответствующее максимуму силы межатомного притяжения F m (рис. 1). Кинетическая единица (атом, группа атомов), которая испытывает критическое смещение – делокализацию, называется возбужденным атомом, а сам подход – моделью возбужденного состояния (моделью делокализованных атомов) [13-16]. Рождение возбужденного атома обусловлено флуктуационной перегруппировкой соседних частиц и носит энтропийный характер [16]. Кинетические единицы могут перейти из основного в возбужденное состояние не только в результате тепловых флуктуаций, но и под механическим и другим внешним воздействием.

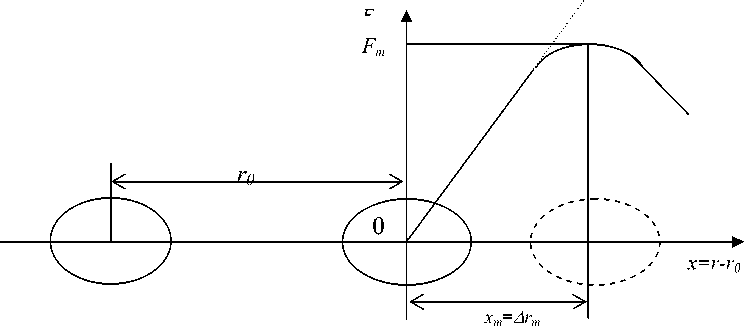
Рис. 1. Схема механизма возбуждения атома (межатомной связи). r_o – равновесное межатомное расстояние. Δ r_m – критическое смещение атома, соответствующее максимуму силы F_m межатомного взаимодействия.

Одним из важных параметров модели является флуктуационный объем системы

∆V e = N e ∆ν e ,                                                 (1)

где N e – число возбужденных атомов, Δv e – элементарный флуктуационный объем, необходимый для возбуждения (делокализации) атома.

Этот минимальный микрообъем определяется главным образом масштабом критического смещения атома Δr m

∆ν e = πd²∆r m ,                                                    (2)

где π d² – площадь эффективного сечения атома, если жидкость представим в виде однородной среды, состоящей из одинаковых взаимодействующих сфер.

По аналогичной формуле через среднее смещение атома Δr выражается средний флуктуационный объем vf =ΔVe/N, приходящийся на одну частицу, v f = πd 2Δr                                           (3)

Таким образом, флуктуационный объем аморфной среды обусловлен критическими отклонениями частиц из равновесных положений – из центров ячеек в результате локальной флуктуации плотности, что связано с локальными упругими деформациями межатомных связей. Поэтому изменение флуктуационного объема может происходить в принципе при постоянном объеме системы V = const.

Уплотнение небольшого кооператива частиц при их локальной флуктуационной перегруппировке может привести к такому его сжатию, что флуктуационный объем, принадлежащий всем молекулам кооператива, аккумулируется в одном месте у одной из частиц. Следовательно, время от времени у любой частицы аморфной среды может образоваться локальный флуктуационный объем v~ , сравнимый с размерами частицы. Будем полагать, что необходимым условием перескока частицы из одного временного равновесного положения в другое является образование в ее окрестности флуктуационного объема v~ , превышающего элементарный объем атомного возбуждения: v~ ≥ Δ v_e .

Таким образом, определение вероятности возбуждения атома сводится к нахождению вероятности образования минимального элементарного флуктуационного микрообъема Δv e у данного атома.

Вероятность возбуждения кинетической единицы

Из модели возбужденного состояния следует, что частицы жидкости и аморфных сред отличаются друг от друга главным образом величиной локального флуктуационного объема, который образуется в их окрестности. Предположим, что число частиц dn , обладающих флуктуационным объемом от v~ до ~ + dv , описывается функцией [6, 17, 18]

dn = A exp

~

где ΔH – энергия, необходимая для образования флуктуационного объема v~ . Она равна работе, совершаемой против внешнего p и внутреннего p i давлений,

A H = (p i + p )v

При данных условиях сумма давлений ( p i + p ) является константой, не зависящей от v~ .

Нормировка производится так, чтобы общее число молекул N в рассматриваемом объеме было равно сумме частиц dn

N

J dn = N откуда для множителя А следует выражение

A J exp

⁽ pi ⁺ p ^)v kT

dv = N ’

A = (p_t + p)N

.

kT

Здесь интегрирование распространено от 0 до ∞, хотя в действительности элементарный флуктуационный объем v~ ограничен как снизу, так и сверху. Следовательно, предполагается, что в жидкости средний флуктуационный объем одинаково далек от обоих пределов – как минимального, так и максимального значений.

Теперь можем найти число возбужденных кинетических единиц N e , обладающих локальным флуктуационным объемом V , превышающим объем атомного возбуждения: V >  A v e ,

7 (pi + p )N

N = ⁱ exp e A v e      kT

( p _i + p )v^v kT

dv = N exp

( P i + P ) A V e

kT

.

В соответствии с равенством (4) работа образования минимального элементарного флуктуационного микрообъема ΔHe, которая может быть названа энтальпией возбуждения атома, определяется выражением

AHe = (pi + p) АVe = Afe + pAVe,(6)

где величина Δε e представляет собой энергию образования микрообъема Δv e в отсутствии внешнего давления (при p i >>  p )

Age = piAVe.(7)

Принимая во внимание (6), из равенства (5) окончательно получаем следующее соотношение для вероятности возбуждения кинетической единицы W е = N e / N

N^      L ( pi + p)AVe I = eXnL Age + p AVe ) ,(8)

N exp L kT J exp I kT J которое можно рассматривать как основное уравнение модели возбужденного состояния жидкостей и стекол.

Формула Коена-Тернбулла в модели возбужденного состояния

Убедимся, что из приведенных выше представлений вытекает известная формула Коена–

Тернбулла [19] для молекулярной подвижности в жидкостях и стеклах

^We = exP I -

b^^ \ , ^vf J

где v o – объем дырки, куда может переместиться молекула, v f = V f / N – средний флуктуационный свободный объем, приходящийся на одну частицу, b –коэффициент, учитывающий перекрытие дырок: 0.5 ≤ b ≤ 1.

Далее будет развито представление о том, что флуктуационный свободный объем V f совпадает с флуктуационным объемом ΔV e в модели возбужденного состояния (см. ниже). Поэтому отношения V f / N и ΔV_e / N в равенствах (9) и (3) обозначаем одинаковым символом v f .

Найдем общий флуктуационный объем ΔV e как сумму флуктуационных объемов любых размеров

N~,l   7 ( Pl + P)N

A V e = J v dn = J i exp _{0        0} kT

(p. + P)v - _ NkT ---vdv =--------- , kT     _l        (P i + P )

откуда средний флуктуационный объем v f = ΔV e / N , приходящийся на молекулу, равен kT

v _f =----------

⁽P i ⁺ P)

.

Подставив (10) в равенство (5), приходим к следующему соотношению

N          ^f A v 7 ,

W e =       = exp I~ I

N         I    v _f ^J

которое с точностью до b ≈ 1 совпадает с уравнением Коена–Тернбулла (9), поскольку величину v f можно интерпретировать как средний флуктуационный свободный объем, приходящийся на частицу,

а Δv e – как объем дырки v o , куда может сместиться частица [13] (см. ниже).

Основное уравнение и соотношение Клаузиуса

Принимая во внимание равенства (2) и (3), эту формулу (11) представим в виде

I     A v |          f A

W _e = exp II = exp I ^ 7 I      v _f J         ^    A r

что по внешнему виду совпадает с уравнением Клаузиуса для вероятности того, что молекула газа пробежит данное расстояние l без столкновений:

w f l

W = exp I--

I 2

,

(12а)

где λ – средняя длина свободного пробега молекулы газа.

Если внимательно проследим за процедурой вывода уравнения Клаузиуса (12а) из общих принципов статистической физики, то увидим, что в принципе нет ограничений для его применения к конденсированному состоянию вещества. Ситуация здесь напоминает распределение Максвелла. Известно, что максвелловский закон распределения молекул газа по скоростям справедлив не только для газов, но и для жидкостей и твердых тел [8].

Тепловое движение в жидкостях сводится к беспорядочным перескокам частиц из одних временных положений равновесия в другие и к их тепловым колебаниям в промежутках между скачками [8]. Шаг за шагом с кратковременными остановками частица блуждает по объему так же беспорядочно, как и в случае беспорядочного теплового движения молекулы газа. Имеется лишь следующее основное (количественное) различие: в жидкостях среднее время оседлой жизни частицы – время кратковременных остановок – существенно больше «времени оседлой жизни» молекулы газа, которое представляет собой длительность столкновения частиц, т.е. ничтожно малую величину.

Таким образом, общий характер беспорядочных перескоков частиц в жидкостях и аморфных средах оказывается примерно таким же, как и в случае газов. Критическое смещение атома или молекулы жидкости из равновесного положения (перед перескоком в дырку) является случайной величиной, как и длина свободного пробега молекулы газа.

С этих позиций для вероятности критического смещения Δr m кинетической единицы жидкости можно вос пол ьзоваться формулой (12), аналогичной уравнению Клаузиуса (12а), где среднее смещение атома A r , как аналог средней длины свободного пробега молекулы газа, зависит от площади его эффективного сечения πd ² и концентрации атомов n = N / V , способных к критическому смещению,

Ar =

nd ² n

Уравнение состояния представляет собой условие баланса, которое требует, чтобы внешнее давление p совместно с внутренним давлением p i уравновешивало тепловое давление p t , действующее на поверхность системы изнутри [6, 20, 21]

p + p i = p t .

Для твердых тел и жидкостей величина p t в классической области (выше температуры Дебая) выражается формулой [6, 20, 22]

U 3 RT

Pt = у -D^- = у —— = 3 YnkT ,

где U_D – дебаевская энергия тепловых колебаний решетки, γ – параметр Грюнайзена, характеризующий нелинейность силы межатомного или межмолекулярного взаимодействий и ангармонизм колебаний решетки, R – газовая постоянная, k – постоянная Больцмана.

Подставив n(p, T) из уравнения состояния (14) с учетом (15) в равенство (13), а затем и (13) в соот- ношение (12), приходим к основному уравнению модели – к уравнению для вероятности процесса делокализации – возбуждения атома Wе = Ne/N

' ⁿ d 2 A r m ) ( P i + p )

, 3 Y J kT

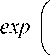
^AE e

+ P ^v e kT

N

---= exp

N что совпадает с полученным выше уравнением (8). Здесь Ne/N – доля возбужденных атомов, Δve – элементарный флуктуационный объем, необходимый для процесса возбуждения атома,

^A v e = ^f 1— ^{1 n} d ^{2 A} r m                                                       ⁽¹⁷⁾

I 3 Y )

а энергия возбуждения (делокализации) атома Δεe равна работе против внутреннего давления pi, обусловленного силами притяжения между атомами, как и в случае (7) Aee = piAve. Под pi следует пони- мать максимальное внутреннее давление, соответствующее максимуму силы межатомного притяжения. Элементарный флуктуационный объем атомного возбуждения (17) обратно пропорционален параметру Грюнайзена. Это означает, что чем больше γ – чем сильнее выражена нелинейность силы межатомного взаимодействия (рис. 1), тем при меньшем флуктуационном объеме Δve может происходить критическое смещение – возбуждение атома (табл. 1).

Таким образом, основное уравнение модели возбужденного состояния можно вывести двумя различными способами (8 и 16). Второй способ, основанный на использовании соотношения (12) типа уравнения Клаузиуса (12а), позволяет получить микроскопическую интерпретацию элементарного объема атомного возбуждения в виде (17).

Как отмечалось выше, важным параметром модели возбужденного состояния жидкостей и аморфных сред является флуктуационный объем системы (1) ∆ V e = N e ∆ν e , объемная доля которого f = ( ΔV e / V ) = ( Δv e / v ) N e / N с учетом (16) определяется равенством

^AE e + p ^A v e 1 ,                                     (18)

kT J где v=V/N – объем, приходящийся на атом. Это выражение можно рассматривать как уравнение состояния.

Дырочная теория жидкостей и стекол в модели возбужденного состояния

Основное соотношение модели возбужденного состояния (16) совпадает с френкелевской формулой для концентрации дырок в жидкости N h / N [8, 21]

N^- exn [- ^£h + ^pvh 1 ,                                           (19)

exp N ( kT )

а равенство (18) – с уравнением состояния в дырочной теории жидкости [8, 21]

f =

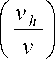
exp

E h + pv h 1

, kT )

где ε h – энергия образования дырки объемом v h , f = V f / V – объемная доля флуктуационного свободного объема V f = ν h N h .

Следовательно, образование дырки свободного объема обусловлено процессом «возбуждения атома» – флуктуационным критическим смещением – делокализацией молекулы, откуда параметры дырочной теории жидкостей совпадают с соответствующими параметрами модели возбужденного состояния, ибо «дырка» представляет собой возбужденный атом [13]:

ν h = ∆ ν e , ε h = ∆ ε e ,        N h = N e ,         V f = ∆ V e .                                         (21)

С этой точки зрения флуктуационный свободный объем V f = ∆ V e не является свободным объемом в традиционном его понимании по Ван-дер-Ваальсу. Поэтому V f целесообразно называть просто «флуктуационным объемом», который образуется благодаря флуктуационным смещениям возбужденных атомов в процессе флуктуации плотности (см. ниже). Френкелевская формула-экспонента (19) для концентрации дырок в жидкости приобретает смысл вероятности процесса возбуждения атома – критического его смещения (16). Следовательно, можно говорить лишь об условных или эффективных флуктуационных дырках.

В ранних работах Френкеля [8] занятый молекулами объем Vo в формуле свободного объема Vf = V – V0 = νh Nh рассматривался как «минимальный объем, который может быть отождествлен с постоян- ной b в теории Ван-дер-Вальса» [8]. Тем самым под Vf подразумевался вандерваальсов свободный объем, представляющий собой пустое пространство между молекулами. Пустой объем между частицами, определенный из данных о коэффициенте упаковки атомов, у аморфных полимеров и стекол составляет около 25-35% от общего объема системы [6, 23, 24]. Его рассматривают как элемент структуры и называют структурно-обусловленным [10], геометрическим [6] свободным объемом.

Френкель [21] в более поздних работах свободному объему жидкости придавал смысл суммарного объема дырок, возникающих при плавлении кристалла (« V o – истинный объем тела при отсутствии дырок») [21]. С этой точки зрения свободный объем равен избыточному объему жидкости в сравнении с объемом твердого тела. Для подавляющего большинства кристаллов увеличение объема при плавлении составляет лишь около 2-4% [25, 26]. Такой избыточный объем обычно называют флуктуационным свободным объемом [6]. По-видимому, он обеспечивает текучесть жидкости и замораживается при переходе аморфного вещества из жидкого в стеклообразное состояние. В самом деле, флуктуационный свободный объем, замороженный при температуре стеклования T = T_g , для различных стеклующихся систем: аморфных органических полимеров [7], неорганических стекол [6], металлических аморфных сплавов [1, 27] составляет 2-4%

V f = I — fg

® const * 0.02 - 0 . 04 ,

T = T g

что на порядок величины меньше геометрического структурно обусловленного свободного объема по Ван-дер-Ваальсу. Физический смысл V f = v h N h определяется главным образом природой зависимости N h ( p , T ).

Таким образом, френкелевские флуктуационные дырки представляют собой эффективные дырки – «возбужденные атомы», которые возникают в процессе плавления кристалла и размягчения стекла как результат делокализации атомов и обеспечивают текучесть системы [28]. Их низкая концентрация в области стеклования при f g ≈ 0.02-0.03 и Δv e / v ≈ 0.6 (табл. 1-5)

N h N

g * 0 . 03 - 0 . 05

объясняется тем, что флуктуации, связанные с критическими смещениями молекул, при низких температурах относятся к редким флуктуациям.

Можно привести определенные аргументы в пользу представления о том, что механизм образования «дырки» – критическое смещение возбужденного атома – служит элементарным актом процессов плавления кристалла и размягчения стекла [14, 28]. Этот механизм играет важную роль в вязком течении стеклообразующих жидкостей. Величина f g ≈ 0.03 (22) определена из данных о вязкости в области стеклования (см. ниже).

Флуктуационный объем и флуктуация плотности

Коэффициент сжимаемости стеклообразующей жидкости κ l можно представить в виде двух слагаемых [6, 8]

kl = kg + kf, где κg отражает «геометрическую» сжимаемость твердого стекла, обусловленную пропорциональным уменьшением межатомных расстояний при всестороннем сжатии, а структурное слагаемое κf, равное сжимаемости флуктуационного объема («флуктуационного свободного объема»), связано с изменением взаимных расположений частиц относительно друг друга в результате их локальных перегруппировок. В величину сжимаемости жидкости доминирующий вклад вносит именно эта структурная составляющая κf, наличием которой объясняется существенно большая сжимаемость жидкостей в сравнении с твердыми телами.

Поэтому обычно принимается вполне приемлемое приближение κ f >>  κ g , откуда, полагая κ l ≈ κ f и используя зависимость f ( p ) из уравнения состояния (16), для сжимаемости жидкости κ l =-( df / dp ) T выводится соотношение [8, 21, 29]

^i«

.

К I = f ---e l kT

Из термодинамики известно, что средний квадрат относительной разности флуктуации плотности выражается формулой

Ap V _ к l kT P / v

Выразив величину f из выражения (23) f = KikT и сопоставив ее с флуктуацией плотности (24), Ave приходим к выводу, что доля флуктуационного объема аморфных сред является функцией относительной флуктуации плотности [6, 29]

f = —

A V e

,

что указывает на тесную связь процесса возбуждения (делокализации) атома с флуктуацией плотности.

Отсюда видно, что в отсутствии флуктуации плотности < Δρ / ρ >² = 0 флуктуационный объем аморфных систем равен нулю f = 0. Этот факт подтверждает приведенное выше представление о том, что флуктуационный объем ∆ V e = N e ∆ ν e (следовательно, флуктуационный свободный объем V f = ∆ V e ) не имеет никакого отношения к традиционному структурно-обусловленному [10] геометрическому [6] свободному объему по Ван-дер-Ваальсу («пустому объему» между молекулами и атомами).

Расчет основных параметров модели возбужденного состояния

В теории флуктуационного свободного объема и в модели возбужденного состояния поведение жидкостей описывается формально одним и тем же уравнением состояния (18). Поэтому, пользуясь известным формализмом теории флуктуационного свободного объема [6], для расчета параметров модели возбужденного состояния можно получить такие же по внешнему виду формулы, что и в случае указанной теории жидкостей и стекол [1, 6].

Доля флуктуационного объема f g . Поскольку флуктуационный объем ΔV e и флуктуационный свободный объем V f совпадают (21), их объемные доли обозначаем одной и той же буквой f , в частности, при температуре стеклования Т = Т_g имеем f = f_g

f g

A V e V

T = T g

V f V

T = T g

Величина f g определяется по экспериментальным данным о вязкости как обратная величина «универсального» параметра С 1 известного уравнения Вильямса-Ландела-Ферри (ВЛФ) [7], описывающего температурную зависимость вязкости и времени релаксации в области стеклования (табл. 1-6) [6, 7],

f„ = —— ~ const ~ 0 . 025 - 0 . 035 ^g C ₁

Это соотношение (25) можно рассматривать как критерий стеклования жидкостей [6, 7]: аморфное вещество переходит из жидкого в твердое стеклообразное состояние, когда доля флуктуационного объема при охлаждении уменьшается до некоторого минимального значения (25).

Расчет элементарного флуктуационного объема Δv e . Обратимся к уравнению (23). Переходя от коэффициента сжимаемости к изотермическому модулю всестороннего сжатия B =1/ κ l , разрешим это уравнение относительно объема атомного возбуждения (объема «дырки») ∆υ e = kT/ f B. Применим это соотношение к области стеклования, где при Т ≤ Т g доля флуктуационного объема остается постоянной f g ≈ const (25),

^V e

kT g f g B

,

где под величиной В будем понимать мгновенный модуль объемного сжатия стекла при Т < Т g , который можно выразить через мгновенный модуль упругости E при одноосной деформации и коэффициент Пуассона µ

B =--- E---

3(1 - 2 Ц )

В справочниках [26, 31, 32] и в научной литературе обычно приводятся экспериментальные данные о величинах E и µ , поэтому для расчета элементарного объема атомного возбуждения Δv e равенство (26) удобнее представить в виде [29, 30]

3 ( 1 - 2 ц )kT g

.

Av„ = ---------------- e           fgE

Здесь значения упругих постоянных E и µ относятся, как правило, к комнатной температуре. Следовательно, формула (27) основана на приближении слабой температурной зависимости этих величин. Результаты расчета Δv_e по этой формуле приведены в таблице 1-5.

Расчет Δε e . Формулу для расчета энергии возбуждения атома Δε e можно получить из уравнения состояния (18), записанного при Т ≤ Т g ,

,     ( A v _e A      |     Ae. + p Av, | .

f „ = ----— exp I - ----e----~— I g к v V     к kT g J

Разрешив это уравнение относительно энтальпии возбуждения атома ΔH e = Δε e + pΔv e (6), имеем

AH = kT (ln — + ln ^v^)

e        g      fgv

Элементарный флуктуационный объем Δv e , который можно рассматривать как объем «дырки», куда может переместиться кинетическая единица (см. ниже), по порядку величины должен быть близок к объему v = V / N , приходящемуся на частицу ( Δv e ≈ v ). Поэтому в равенстве (28) вторым слагаемым в скобках можно пренебречь: ln (1/ f g )>> ln ( Δv e / v ), откуда (28) упрощается

A H e = kT g ln(1/ f).                                             (1.29)

Принимая во внимание формулу (6), где при обычном атмосферном внешнем давлении p ≈ 1 атм можно принять p i >>  p , поскольку внутреннее давление жидкостей и твердых тел, обусловленное силами межатомного притяжения, составляет значительную величину p i ≈ 10⁴-10⁵ атм. [6,20]. Поэтому при атмосферном давлении p ≈ 1 атм энтальпия ΔH e и энергия Δε e возбуждения атома фактически совпадают A H _e = (p i + р )Au_e = p i Au_e = A e _e.

Таким образом, энергию атомного возбуждения можно рассчитывать по формуле (29) при ЛН_е = Δε e

A e e = kT g in^lhf)                                                 (30)

Результаты расчета Δε e по этой формуле приведены в таблицах 1-6. Рассмотрим расчет Δε e по данным о коэффициенте поверхностного натяжения σ и атомном объеме v .

Таблица 1

Параметры модели возбужденного состояния для калиевоборатных стекол K 2 O-B 2 O 3

K 2 O, мол.%	T g , K	р	f g	AV e , К3	A v e /v	A se , кДж/моль
0	578	0.262	0.034	20	0.56	13
1.1	582	0.292	0.034	16	0.48	13
2.5	588	0.293	0.033	15	0.48	13
3.9	597	0.293	0.032	14	0.48	13
8.5	623	0.293	0.030	13	0.48	14
13.0	658	0.295	0.030	13	0.47	15
18.0	685	0.301	0.029	13	0.46	16
22.8	711	0.295	0.028	13	0.47	16
28.2	723	0.288	0.027	12	0.49	17
33.5	706	0.303	0.026	11	0.45	17

Таблица 2

Параметры модели возбужденного состояния для аморфных органических полимеров

Полимер	T g , K	Р	f g	A ve/v	A v e , К3	A se , кДж/моль
полипропилен	258	0.32	0.035	0.41	26	5
полистирол	363	0.34	0.030	0.36	39	7
полиметилметакрилат	373	0.33	0.030	0.38	25	8
полиформальдегид	213	0.31	0.037	0.43	12	4
поликарбонат	420	0.38	0.036	0.26	33	7
полиэтилен	248	0.36	0.032	0.31	30	5

Таблица 3

Доля флуктуационного объема f g и коэффициент Пуассона р для сульфатнофосфатных стекол NaPO 3 -RSO 4 (R=Zn, Li, Na, K)

RSO 4 , мол. %	T g , K	f g	Р	A v e /v	A v e , A 3	A ee , кДж/моль
NaPO 3	523	0.016	0.294	0.48	16	15
ZnSO 4 – 10	493	0.018	0.288	0.49	12	13

20	505	0.019	0.284	0.50	12	14
30	510	0.020	0.273	0.53	11	14
40	515	0.020	0.259	0.27	10	14
LiSO 4 – 10	451	0.014	0.300	0.46	13	13
20	447	0.013	0.303	0.45	14	13
30	429	0.014	0.304	0.45	12	12
Na 2 SO 4 –10	496	0.016	0.299	0.46	14	14
20	493	0.016	0.292	0.48	15	14
30	490	0.015	0.288	0.49	17	14
K 2 SO 4 – 10	444	0.013	0.316	0.42	16	13
20	453	0.014	0.316	0.42	15	13

Таблица 4

Доля флуктуационного объема f g и коэффициент Пуассона µ для кварцевого стекла SiO 2

и щелочносиликатных стекол R2O-SiO2 (R=Li, Na, K)

Стекло	T g , K	f g	µ	Δ ve /v	Δ v e , Å3	Δ εe , кДж/моль
SiO 2	1423	0.03	0.170	0.85	17	39
R 2 O-SiO 2
Li 2 O, мол.%, 28.6	688	0.028	0.205	0.73	8	19
30.0	686	0.027	0.208	0.72	8	19
32.6	684	0.029	0.213	0.71	7	18
35.9	680	0.029	0.20	0.75	7	18
41.3	675	0.029	0.231	0.66	6	17
Na 2 O, мол.%, 19.6	744	0.029	0.234	0.65	10	19
29.45	715	0.028	0.254	0.59	9	18
30.1	713	0.028	0.255	0.59	9	18
32.9	704	0.028	0.255	0.59	9	18
36.3	694	0.029	0.255	0.59	8	18
K2O, мол.%, 16.7		0.030	0.236	0.64	11	20
18.8	760	0.029	0.244	0.62	11	20
21.4	745	0.029	0.254	0.59	11	19
26.9	733	0.028	0.275	0.53	11	18
28.7	728	0.028	0.281	0.51	11	17
33	715	0.027	0.295	0.47	11	17

Таблица 5

Параметры модели возбужденного состояния для халькогенидных стекол

Стекло, ат. %	T g , K	fg	µ	Δ v e , Å3	Δ ve/v	Δ εe , кДж/моль
As 10 S 90	302	0.010	0.376	56	0.27	8
As 20 S 80	362	0.022	0.305	29	0.45	9
As 28 S 72	408	0.024	0.289	27	0.49	10
As 40 S 60	453	0.030	0.290	16	0.49	11
As 5 Se 95	316	0.021	0.326	21	0.39	8
As 10 S 90	353	0.020	0.331	22	0.38	9
As 30 S 70	406	0.031	0.290	15	0.49	9
As 40 Se 60	456	0.029	0.260	18	0.57	11
As 50 Se 50	442	0.024	0.300	24	0.46	11

Поверхностное натяжение жидкости σ равно работе, необходимой для того чтобы путем растяжения поверхностного слоя увеличить его поверхность на единицу площади (1 см2). Средние межатомные расстояния и силы межатомного взаимодействия в твердых телах и соответствующих жидкостях примерно одинаковы. Объясняется это тем, что в жидкостях ближний порядок в первом приближении такой же, как и в твердых телах. Поэтому понятие поверхностного натяжения имеет смысл и для твердых тел.

Френкель [21] работу разрыва стержня площадью сечения 1 см2 на две половинки, т.е. работу образования свободной поверхности в 2 см2 при отрыве друг от друга двух единичных атомных площадок по 1 см2, определяет соотношением

2σ∫pi(x)dx ≅ pim∆rm, где pi(x) – внутреннее давление, равное силе притяжения между частицами, отнесенной к единице площади, x – расстояние между единичными площадками, pim – максимальное внутреннее давление, соответствующее предельному удлинению связи между частицами Δrm.

Таблица 6

Параметры модели возбужденного состояния для металлических стекол – аморфных сплавов ( C 1 и C 2 – параметры уравнения ВЛФ [7])

№	Аморфный сплав	T g , K	C 1	C 2 , K	fg	Δε e , кДж/моль
1	Ni	430	35	135	0.029	13
2	Ni 62.4 Nb 37.6	945	40	135	0.025	29
3	Ni 75 Si 8 B 17	782	38	112	0.026	24
4	Fe91B9	600	53	87	0.019	20
5	Fe 89 B 11	640	37	125	0.027	19
6	Fe 83 B 17	760	38	122	0.026	23
7	Fe 41.5 Ni 41.5 B 17	720	38	119	0.026	22
8	Fe79Si10 B11	818	38	117	0.026	25
9	Fe 80 P 13 C 7	736	38	120	0.026	22
10	Pd 82 Si 18	657	37	100	0.027	20
11	Pd 40 Ni 40 P 20	602	39	93	0.026	18
12	Pt 60 Ni 15 P 25	500	37	95	0.027	15
13	Te	290	41	92	0.024	9
14	Co 75 Si 15 B 10	785	38	110	0.026	24
15	Ge	750	39	50	0.026	23

Таблица 7

Поверхностное натяжение σ и параметры модели возбужденного состояния аморфных полимеров (ПС и ПБ) и неорганических стекол (использованы данные [29, 33])

Стекло	T g , K	f g	σ ∙103, Дж/м3	VA ∙106, м3/моль	Δεe *, кДж/моль
ПС	370	0.032	173	6.3	10/10.6
ПБ	189	0.026	110	5.5	5.8/5.8
Li 2 O∙3B 2 O 3	693	0.019	406	6.1	22.8/23.1
F2	705	0.044	250	9.1	18.5/18.4
SF64	851	0.054	290	8.4	20.3/20.7
8209	785	0.022	340	8.6	24.2/24.9
8330	803	0.029	340	8.5	24.0/24.0
8558	948	0.02	430	8.2	29.5/31.0
Li 2 O-SiO 2
Li 2 O, мол.%
20	697	0.028	310	7.9	20.8/20.7
30	686	0.027	314	7.3	20.0/20.6
35.9	680	0.029	323	6.9	19.9/20.0
41.3	675	0.029	334	6.6	19.9/19.9
Na 2 O-SiO 2
Na 2 O, мол.%
19.6	744	0.09	276	8.9	20.1/21.9
30.1	713	0.028	282	8.9	20.4/21.2
32.9	704	0.028	284	8.8	20.5/20.9
36.2	694	0.029	286	8.8	20.6/20.4

Обозначение стекол – по каталогу фирмы «Schott» [33]: F2 – флинтглас, SF64 – тяжелый флинт, 8509 – телевизионный экран, 8330 – стекло «Дуран-50», 8558 – стекло «Керан». ПС – полистирол, ПБ – полибутадиен. * В числителе – расчет по уравнению (31), в знаменателе – по уравнению (30).

Внутреннее давление p_i полностью определяется потенциальным полем, созданным ближайшим окружением частицы (ближним порядком), и быстро убывает с расстоянием между атомами. Поэтому в первом приближении p i ( x ) можно заменить на p im , а dx – на величину Δr m (см. выше).

При переходе от единичных площадок к предельной деформации связи между соседними атомами вместо σ следует брать атомарное поверхностное натяжение σ A , равное произведению σ на площадь сечения атома πd² , 2 σ A = 2 σπ d² = p im ( π d²∆r m ) ≅ p im ∆υ e = ∆ ε e . . Выразив площадь сечения атома πd² через атомный объем v ^2/3, приходим к выводу о том, что энергию возбуждения атома можно рассчитать по данным о поверхностном натяжении и атомном объеме [29, 33]

∆ ε e = 2 σ υ^2/3 N ^1/3 A , (31) где N A – число Авогадро (энергия Δε e отнесена к одному молю).

Атомный объем стекол вычисляется по плотности ρ и средней массе атома M

M zM v= , A= i i ρ ∑ zini zi и Mi – молярная доля и молярная масса i-го окисла, соответственно ni – число атомов в i-том окисле.

Несмотря на приближенный характер формулы (31), у ряда стеклообразных полимеров (полистирол, полибутадиен) и неорганических стекол расчет энергии возбуждения атома Δε_e по этой формуле (31) на основе данных о поверхностном натяжении и атомном объеме хорошо согласуется со значениями Δε e , полученными по соотношению модели возбужденного состояния (30) (табл. 7).

Природа возбуждения кинетической единицы в стеклах и аморфных полимерах

Низкие значения энергии возбуждения атома Δε e ≅ 20-25 кДж/моль и объема атомного возбуждения Δv e ≅ 8-12ų в силикатных и других неорганических стеклах (табл. 1-6) указывают на тот факт, что «образование возбужденного атома» в этих системах представляет собой мелкомасштабный низкоэнергетический процесс.

Известны, по крайней мере, три релаксационных процесса в силикатных стеклах с низкой энергией активации около 20 кДж/моль (5 ккал/моль). Во-первых, это первая стадия уплотнения стекол под высоким давлением при 20oC и обратный процесс их термостимулируемого разуплотнения, основные закономерности которых удовлетворительно описываются дырочной моделью (с энергией образования «дырки» 20-23 кДж/моль) [6, 34]. Предполагается, что уплотнение силикатных стекол под давлением на первом этапе обусловлено низкоактивационной деформацией кремнекислородной сетки [6, 34].

Во-вторых, в исследованиях внутреннего трения, а также диэлектрических потерь в силикатных стеклах наблюдается релаксационный процесс с такой же низкой энергией активации 20 кДж/моль [35]. Обычно предлагаемые механизмы данного релаксационного процесса сводятся к локальным деформациям кремнекислородной сетки в результате смещения мостикового атома кислорода в мостике Si-O-Si перпендикулярно [36] или вдоль [37] направления цепочки из валентных связей Si-O-Si.

В-третьих, по Мюллеру [38], переключению валентных связей в силикатных стеклах предшествует критическое низкоактивационное растяжение структурной сетки с энергией активации ~ 20 кДж/моль (2-7 ккал/моль) [39]. В такой низкоактивационной деформации кремнекислородной сетки важную роль играют критические смещения мостиковых атомов кислорода.

Мюллером [39] впервые развито представление о том, что механизм вязкого течения стекол и их расплавов заключается в активационном переключении валентных связей между атомами. Эта идея получила дальнейшее развитие в валентно-конфигурационной теории Немилова [20, 40, 41]. На рис. 2 приводится схема переключения валентной связи в силикатном стекле по Немилову [41]. Когда мостиковый ион кислорода в мостике Si-O-Si в результате поперечных тепловых колебаний оказывается достаточно близко к ненасыщенному иону кремния Si+ (рис. 2в), может произойти переключение валентной связи Si-O-Si (рис. 2с).

По-видимому, приведенная выше мюллеровская энергия активации около 20 кДж/моль относится к процессу локальной предельной деформации кремнекислородной сетки, обусловленной критическим смещением мостикового атома кислорода Δr m (рис. 2 в).

Для силикатных стекол между основными параметрами модели возбужденного состояния ( Δv_e , Δε e ) и валентно-конфигурационной теории вязкого течения ( v η , ΔF η ) [40] в области стеклования наблюдаются корреляции [42, 43]

Δv e ≈ const ≈ 0 . 6

Δε                .

^e ≈ const ≈ 0 . 1

v

Линейный размер ν η ^1/3

η

ΔFη объема частицы, преодолевающей потенциальный барьер при вязком тече- нии, соответствует масштабу элементарного активированного смещения мостикового атома кислорода в мостике Si-O-Si перед переключением соседних связей в направлении сдвигающего напряжения (рис. 2в) [41], а свободная энергия активации вязкого течения ΔFη(Tg) имеет смысл флуктуационного изменения упругой энергии, при котором упругий элемент структуры превращается в вязкий элемент.

Исходя из этих и других данных [6, 34], естественно предположить, что «образование возбужденного атома» в неорганических стеклах и их расплавах соответствует низкоактивационному мелкомасштабному процессу локальной предельной упругой деформации структурной сетки, обусловленной критическим смещением мостикового атома. В силикатных стеклах «процесс возбуждения ато- ма» представляет собой критическое смещение мостикового атома кислорода в структурном фрагменте кремнекислородной сетки Si-O-Si перед переключением валентной связи (рис. 2). Вместо «возбуждения – делокализации атома» можно говорить о «возбуждении межатомной связи», ибо критическое смещение мостикового атома связано с предельной локальной упругой деформацией межатомных связей (рис. 1 и 2).

Si

(а)

О

O

Si

O

Si +

O-

Si

I

(c)

Si OSi

OO

SiO Si

Рис. 2. Схема образования возбужденного атома в силикатном стекле [2]

У линейных аморфных полимеров, по данным Сангадиева [44], объем атомного возбуждения при 20^оС составляет около 30-40 ų (табл. 2). Эти данные, по-видимому, несколько занижены. Расчет, основанный на данных о величинах E , µ , и T g , взятых из других работ [24, 45, 46], для типичных линейных стеклообразных полимеров: полиэтилена (ПЭ), полипропилена (ПП), поливинилхлорида (ПВХ), полиметилметакрилата (ПММА), полистирола (ПС), приводит к значениям

∆νe ≈ 50 – 70Å3, что существенно меньше объема сегмента полимерной макромолекулы и по порядку величины приближается к объему мономерного соединительного звена основной цепи макромолекулы. Энергия возбуждения атома для них сравнима с энергией межмолекулярного взаимодействия в аморфных полимерах Δεe ≅ 6 – 12 кДж/моль.

У сетчатых эпоксидных полимеров типа модифицированной эпоксидной смолы ЭД-16 значения основных параметров модели возбужденного состояния

∆νe ≈ 45 – 74Å3, Δεe = 11 кДж/моль имеют такой же порядок величины, что и у линейных аморфных полимеров. Для указанных эпоксидных полимеров в расчетах приняты следующие данные [47]: Tg = 358 K, µ = 0.33-0.37, E = (28-35)108 Па и fg = 0.025. Ниже приведены значения Δve для стеклообразных полимеров при низкой температуре 4.2 K [48, 49].

Полимер	ПЭ	ПП	ПВХ	ПММА	ПС
Δv e , Å3	13	20	27	30	37

Как видно, при переходе от ПЭ к полимерным стеклам, как ПВХ, ПП, ПС, и ПММА, звенья которых отличаются от звена ПЭ содержанием вместо одного атома водорода таких атомных групп, как Cl, СН 3 , С 6 Н 5 и СООСН 3 , соответственно значения Δv e меняются в пределах от 13 до 37 ų (при 4.2 K). На основе данных о параметрах Δv e и Δε e можно предположить, что «процессу возбуждения атома» в стеклообразных полимерах соответствует предельное смещение небольшого участка основной цепи макромолекулы – вероятно, группа атомов в соединительном звене (типа группы -CH 2 -). Низкое значение Δε e свидетельствует о том, что критическое смещение групп атомов связано со сравнительно небольшими силами межмолекулярного взаимодействия.

В последние годы методом аннигиляции позитронов проведены измерения параметров теории флуктуационного свободного объема стеклообразных полимеров [50-52]. Интересно отметить, что для эпоксидного полимера получены следующие значения объема флуктуационной дырки vh и доли флуктуационного свободного объема fg, замороженной при температуре стеклования [50]

vh = 62 Å3 и fg = 0.029, которые находятся в согласии с результатами расчета по модели возбужденного состояния по формулам (27) и (25), поскольку объем дырки совпадает с объемом атомного возбуждения: vh = Δve (21).

По-видимому, ловушками позитронов служат те микрообласти структуры полимерных стекол, где располагаются критически деформированные межмолекулярные связи (возбужденные атомы – «дырки»).

Молекулярная подвижность и локальные возбуждения в упругой сплошной среде

Параметры модели возбужденного состояния, которые представляют собой дискретные микроскопические величины, оказываются функциями макроскопических упругих постоянных. Например, микроскопический элементарный флуктуационный объем Δv e , необходимый для критического смещения – делокализации атома, рассчитывается по формуле (27) из экспериментальных данных о модуле упругости и коэффициенте Пуассона о параметрах теории упругости, которая описывает поведение упругой сплошной среды – континуума. Здесь наблюдается некоторая непоследовательность, а именно перемешивание молекулярно-кинетического (дискретного) подхода и подхода, исходящего из теории упругого континуума. Тем не менее без особого обоснования на практике часто используется такое объединение указанных подходов, что приводит, как правило, к вполне разумным результатам.

В последнее время в работах Немилова [53-55] предложено обоснование сочетания континуальных теорий (теорий упругости и гидродинамики) и молекулярно-кинетических дискретных моделей при анализе вязкого течения и стеклования жидкостей. Развито представление о том, что «смещения частиц при преодолении потенциальных барьеров есть реальные молекулярные процессы, сводящиеся к локальным возбуждениям (локальным упругим деформациям). Окружающая среда реагирует на такое возмущение как непрерывный упругий континуум, в котором тензоры упругих напряжений и деформаций описываются в рамках теории сплошной среды – теории упругого (или вязкого) континуума».

В связи с этим наша модель возбужденного состояния естественно вписывается в данную концепцию. Возбуждение атома – его критическое смещение из равновесного положения – представляет собой локальное возбуждение (локальную упругую деформацию) в упругой сплошной среде, характеризующейся определенными упругими постоянными. Отсюда понятно, почему элементарный объем атомного возбуждения оказывается связанным с модулем упругости и коэффициентом Пуассона (27). Моделирование процесса вязкого течения при сочетании молекулярно-кинетических представлений и континуальных теорий приводит к соотношению Немилова [53, 55]

∆ F η = GV η , (32) которое дает возможность рассчитать объем частицы V η , преодолевающей барьер, из данных о мгновенном модуле сдвига стекла G и о свободной энергии активации вязкого течения ΔF_η при температуре стеклования.

Потенциальный барьер, который преодолевает частица, ответственная за вязкое течение, рассчитывается как работа локальной упругой деформации в сплошной среде, имеющей модуль сдвига G . Оказывается, что для неорганических стекол различной природы смещения мостиковых атомов -О-, -F-, -S- и -Se-, вычисленные из данных о вязкости и упругости, совпадают с радиусами кислорода, фтора, серы и селена, полученными прямыми структурными методами [55].

При выводе равенства (32) допускалось [53], что время релаксации Максвелла τ M = η / G равно обратной величине константы скорости мономолекулярного процесса в среде, имеющей мгновенный модуль упругости G ( η – коэффициент сдвиговой вязкости).

Недавно Немилов [54, 55] вывел данное соотношение (32) в рамках теорий упругости и гидродинамики без привлечения указанного выше допущения относительно максвелловского времени релаксации. Рассмотрим оценку энергии возбуждения атома Δε_e как работу его критического смещения – предельной деформации межатомной связи Δr m в упругой сплошной среде (рис. 1)

1 (33) e 2m m где Fm – сила, необходимая для критической деформации Δrm. Она определяется по закону Гука, который в первом приближении применим вплоть до предельной деформации Δrm .

Выразив силу F m через максимальное внутреннее давление p im = F m / πd ², где πd ² – площадь сечения атома, и принимая во внимание Δv e ≈ πd ² Δr m , равенство (33) перепишем в виде

AS e = у р_ш A V e                                 ⁽³⁴⁾

Задача сводится в основном к необходимости расчета p im .

Внутреннее давление p_i = ( dU / dV ) _T , обусловленное силами межатомного притяжения, представляет собой упругую реакцию решетки на ее всестороннее растяжение или сжатие, поскольку внутренняя энергия U ( V ) слагается из энергий связей, объединивших атомы в твердое тело [6]. Поэтому максимальное внутреннее давление p im можно оценить по закону Гука [6, 20]

1 Pm ~ , E 6 / где величина 1/6γ равна предельной упругой деформации 1/6γ = Δrm/ro [56, 57], γ – параметр Грюнайзена.

Используя для γ формулу Беломестных-Теслевой [58]

3 ( 1 + A ) ,

Y = —I             I

2 ( 2 - 3 a J приходим к следующему соотношению для pim

( 2 - 3 a ) _F = --------- E

9 ( 1 + A )

pim

Следовательно, в выражении для энергии возбуждения атома (34) как p im , так и Δv e в соответствии с зависимостями (27) и (35) являются функциями параметров теории упругости E и µ .

Рассчитаем эти параметры для натриевосиликатного стекла Na₂O-SiO₂ с содержанием окиси натрия 30.1 мол.% Na 2 O.

p = ^{(2 - 3 A} ) E = 718 • 10 ^{7 (Н/} м^{2 )} ,

‘^m    9(1 + a )

3(1 - 2 a ) RT ₂

7 (м³/моль).

A v_e = —-----—--- g- = 51 .6 • 10

^e            f g E

Данные об упругих постоянных этого стекла E = 6340∙10⁷ Н/м², μ = 0.244 взяты из справочника [32], а о величинах T g = 744K и f g = 0.029 – из табл. 4. Оценка работы критического смещения атома в упругой сплошной среде (34) для данного стекла с учетом приведенных значений p_im и Δv_e

AS = 1P,aVv„ = 18 .5 кДж/моль e2ime согласуется удовлетворительно с расчетом Δεe по формуле модели возбужденного состояния (30) (табл. 4)

A e e =R T g ln(1/ / g ) = 18 кДж/моль.

У рассматриваемого натриевосиликатного стекла T g = 744K и f g = 0.029.

Таким образом, модель возбужденного состояния определенным образом связана с локальным элементарным возбуждением в упругой сплошной среде [55].

Заключение

Рассмотрено развитие отдельных аспектов модели возбужденного состояния жидкостей и стекол. Образование элементарного флуктуационного объема, необходимого для возбуждения (делокализации) атома, обусловлено локальной флуктуацией плотности. Показано, что основное уравнение модели возбужденного состояния можно вывести двумя различными способами. Рассчитаны параметры данной модели для неорганических стекол, аморфных органических полимеров и металлических аморфных сплавов.

Из сравнения дырочной теории жидкости с моделью возбужденного состояния следует, что образование дырки обусловлено флуктуационным смещением кинетической единицы, соответствующим максимуму силы межатомного притяжения. Такое критическое смещение кинетической единицы (атома, группы атомов) рассматривается как «процесс возбуждения атома». В силикатных стеклах он представляет собой критическое смещение мостикового атома кислорода в мостике Si-O-Si (рис. 2), а в полимерных углеводородах – предельное смещение соединительного звена (типа -CH 2 -) в основной цепи макромолекулы. Согласно предлагаемой интерпретации, понятие о флуктуационной дырке в жидкостях и аморфных средах принимает условный характер: «дырка» по существу представляет собой «возбужденный атом».

Модель возбужденного состояния может быть использована при интерпретации перехода стекло-жидкость [11, 13], кристалл-жидкость [14, 28], температурной зависимости вязкого течения стекло- образующих жидкостей [15, 42, 59], пластичности стекол [34, 56], ангармонизма колебаний решетки и нелинейности силы межатомного взаимодействия [13, 56, 57].