Модели анализа функционирования производственных корпораций
Автор: Меерсон В.Э.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Информационные технологии, моделирование и управление
Статья в выпуске: 3 (57), 2013 года.
Бесплатный доступ
В статье представлены модели анализа потокораспределения целевого продукта в установившемся режиме функционирования производственной корпорации. Рассмотрено получение модели установившегося потокораспределения целевого продукта производственной корпорации с учетом переменности потерь в участках сети на основе вариационного принципа.
Производственная корпорация, целевой продукт, энергетический узел, модель потокораспределения
Короткий адрес: https://sciup.org/14040095
IDR: 14040095 | УДК: 681.3
Текст научной статьи Модели анализа функционирования производственных корпораций
Структурное оформление производственных корпораций (ПК) предполагает наличие в их составе разнообразных по назначению подсистем и особенно это касается абонентских (пользовательских) подсистем [3]. Присутствие в последних различного рода активных элементов (подсистем принятия решений) приводит к необходимости представления структурных моделей ПК как моделей объектов с регулируемыми параметрами.
Исследуемый объект представляет собой некоторый фрагмент полной системы (ИФС, совокупность подающих целевого продукта (ЦП)), ограниченный узлами, через которые осуществляется обмен транспортируемой средой между ним и метасистемой. Такие узлы в дальнейшем будем называть энергетическими узлами (ЭУ) согласно терминологии, принятой в [2]. Несмотря на то, что производственная корпорация (ПК) обычно считается закрытой системой, потери ЦП в окружающую среду при транспортировке, восполняемой со складов и т. п., все равно существуют как нормируемые потери.
Необходимо иметь в виду, что не все активные элементы (базы, склады и т. п.) в составе ПК можно квалифицировать как энергоузлы. При моделировании будем различать источники питания и источники расхода ЦП. Применительно к ПК все активные элементы, которые обеспечивают перемещение ЦП в системе, классифицируются как источники кинетической энергии, размещаются на участках (дугах) графа и относятся к источникам расхода. Второй класс активных элементов поддерживает заданное количество ЦП в сети,
постоянно пополняя его из запасов, хранящихся на базе, складе и т. п. Этот тип элементов классифицируется как источник потенциальной энергии, относится к источникам напора ЦП, размещается в узлах ПК, которые и называются энергетическими. В структурный состав ИФС входят также подсистемы потребителей (стоки) и участки, стыкующиеся в узлах. Участки состоят из магистралей ЦП, являющихся кинематическими связями для потока,
определяющих его движение.
Исследуемый фрагмент системы ограни-
чен множеством
z J π ( f )
∪ Jz ∪ Jz η ( P ) η ( q )
∪ J
z η ( f )
энергоузлов, содержащим подмножества:
z - источников и z z z - J π ( f ) J η ( P ) ∪ J η ( q ) ∪ J η ( f )
стоков (потребителей), связанных между собой системой трубопроводов. При индексации множества верхний индекс показывает, что множество элементов системы принадлежит к зоне, то есть автономному объекту для моделирования. Нижний индекс определяет характер элемента ( η - потребитель, ΑП; π - источник питания; χ - энергетически нейтральный узел или узел ветвления, то есть без обмена ЦП с метасистемой). В скобках помечен параметр, фиксируемый в качестве исходных данных.
Поскольку все элементы сети обладают однозначными h(Q) характеристиками, задание одного из параметров h или Q для всех элементов системы однозначно определяет ее состояние покоя (стационарный режим), а при задании возмущений, то есть изменений тех или иных параметров от времени (например изменений количества подаваемого (отбирае-
мого) ЦП или изменение в правилах принятия решений) устанавливает траекторию движения (нестационарный режим). К параметрам системы в общем случае относятся и неизбежные переменные потери ЦП при транспортировке, однако здесь для транспортируемой среды пока предполагается отсутствие потерь.
Совокупность объемных расходов ЦП g (в источниках, стоках) и Q (на участках) однозначно определяет стационарный режим течения ЦП в системе. В нестационарном режиме задаваемыми параметрами являются, кроме того, S( t ) и Q - dQdr .
На поток ЦП в любом элементе по аналогии с механикой действуют следующие силы: количество ЦП, подаваемое из источников питания (базы, склады и т. п.) Hj, je tz ; противо- n(f)
давление стоков Hj, j e jz jz jz ; по- Jn ( P ) - Jn ( q ) - Jn ( f )
тери ЦП (отходы) на n участках ИФС (i e ^ z );
силы инерции при транспортировке ЦП.
Учет взаимосвязей в данной вариационной задаче осуществляется посредством введения неопределенных множителей Лагранжа, которые в предмете исследования приобретают смысл узловых потенциалов. Для формирования модели потокораспреде-ления ЦП достаточно исключить неопределенные множители Лагранжа для узлов с нефиксированным потенциалом.
Объединяя подсистемы контурных и цепных уравнений, а также дополнив их подсистемой уравнений узловых балансов (условий неразрывности), получаем модель неустановившегося потокораспределения ЦП, которая имеет следующую векторноматричную форму записи:
где:
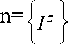
{ __ yx //"xx u(k)\ /r'\u(k] Д. u(k] I _.t (k) . i т Tu(k)
R n(d) + R (Q) n(d) / X Q n x 1 + E n(d) x QnxJ- M p x e x H e x 1 ± Z H(Q) 1 ;
i
u(k)k Du(k) xC>u(k)i-n yHfOY‘(k)-
K r x n x KR n(d) + R(Q)n(d) Г Qn x 1 + E n(d) x QnxJ J- U r x 1 ± Z H(Q)i ;
A x Qu(k)]
гх m x n Xn x 1
аW • gm x 1;
m=
. Jn ( q )
- J x } ;
e = („ . ,Tz ..,z 1 - число энергоузлов с
1 Jn(f) -Jn(P) -Jn(f) } фиксируемым (задаваемым) потенциалом; p -число независимых цепей в расчетной схеме (p=e-1); Ri = siQ|“ 1 - элемент диагональной матрицы, выражающий пропускную способность пассивного элемента; Si -пропускная
способность участка 1; R(Q) i - элемент диа
гональной матрицы, выражающий перемен
ную нагрузку активных элементов (базы, скла
ды и т. п.), установленного на участке i;
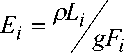
производная расхода ЦП по вре
мени участка i, вычисляемая по результатам двух предыдущих итераций (k-1) и (k-2) в процессе решения; g - ускорение свободного падения; р - плотность потока транспортируемо
го ЦП; L i , F i - длина и пропускная способность участка i соответственно; H , g - матрицы-столбцы фиксируемых в качестве граничных условий (во времени) значений узлового потенциала и отбора (притока) для энер
гоузла j; Z H ( Q ) U ( k ) - сумма напоров (количеств) ЦП питающих элементов, размещаемых на участке i, которые входят в соответствующую независимую цепь или контур, причем знак (+) принимается при совпадении направления действия активного элемента с направлением потока ЦП на участке и знак (-) в противном случае; u(k) - номер итерации двойного цикла (внешний цикл (k) определяет шаг интегрирования по времени, а в пределах внутреннего цикла (u) выполняется расчет объекта как системы с сосредоточенными параметрами) C, K, A. - матрицы смежности независимых цепей, контуров и матрица инциденций соответственно; М - матрица маршрутов; “t” -символ транспонирования; нижние индексы указывают на число строк и столбцов матриц соответственно; “d” - признак диагональной матрицы; “1” - признак матрицы-столбца.
Модель (1)-(3) является в определенной степени приближенной, поскольку скорости изменения расхода ЦП в ней учитываются только для пассивных участков.
Модель установившегося потоко-распределения ЦП может быть получена из (1)-(3) посредством исключения составляющих, зависящих от времени и, кроме того,
в этом случае отпадает необходимость внешнего итеративного цикла:
If u 1 u I t . и
Cp x n x у Rn ( d ) + R ( Q ) n ( d ) J x Qn x1J Mp x e x He x X-^ x H ( Q ) , ; (4)
K r . . x{( R n. , + R ( Q ) nd ,> Q U J- 0 r xi ± E H (Q ) ■ ; (5) i
A x O" - g ; (6) m x n ^„ x , g m x ,
Неуч ет переменности потерь ЦП для участка магистрального пути сети вследствие взаимодействия с окружающей средой, которая имеет место для реальных ПК, может привести при моделировании производственных процессов к значительным погрешностям. Поэтому требуется обобщение, прежде всего модели (4)-(6), на случай потерь ЦП при транспортировке.
По аналогии с известной в гидравлике формулой Дарси-Вейсбаха [1] запишем, что потери ЦП ADi участка магистрального пути i с пропускной способностью D i и длиной L i при переменных потерях ЦП T(x), где х -линейная координата участка сети, можно
О 1 R . О а г
A P . - s^ 1 j T ( x ) dx - s^ TL; (7)
D T- 0 Df T- где T(x), T - переменные и усредненные по длине х участка потери ЦП соответственно;
- нормированные потери ЦП для приве- т ст
дения расхода ЦП к стандартным условиям функционирования ПК.
Поскольку режим функционирования ПК установившийся, необходимо в рамках общей постановки исключить силы инерции.
Для определения неопределенных множителей Лагранжа в задаче с такой постановкой необходимо ввести дополнительные граничные условия в узлах [j, j+1], инцидентных участку i:
T ' при x=0- потери ЦП в начальном узле;
T "при x - потериЦП в конечномузле;
T И
T
при 0
Тогда математическая модель установившегося потокораспределения ЦП с учетом переменности их потерь примет вид:
представить в виде:
{ [( R n ( d ) + R ( Q ) n ( d ) ) x Q U x i C p X " 1 1 O
O
x-----
Rn 2( d )
x J L - M‘ p x e x H e x l ± 2 H ( Q ) U Q n 2 x 1 1
К Jo X [(Rn(d) + R(Q) "(d))x Qnx1 L O x"^ 1x1-0 +
Krx " 1О x " 2 x---------~---------fx- x— -Orx1 ±1H (Q X
[ O J Rn 2( d) Qn 2x1
Amxn 1{Amxn2 }x Q - gmx1
Qn 2 x 1
E. (d) x(B" (d) x®" x1+ Щ)--A txxm x Tmx"(11)
*
Amxn x Qnn(d) x T"x1 - Amx" x Q"d) x T"x1 - gm(d) x Tmx1 - gm(d) x Tmx1
где обозначения аналогичны (1)-(3).
Переменность потерь ЦП вследствие взаимодействия с окружающей средой может быть обусловлена как технологическими, так и другими факторами, причем в последнем случае, рассматриваемом ниже, можно допустить условие T0=const. Если допустить постоянство коэффициента потерь ЦП, то для принятых граничных условий параметр Т(х) можно записать в виде:
T ( x ) - T о + ( t ‘ - T o ) exp [- k n Dx I ( MC p ) J, , (13)
а потери ЦП в конечном узле j+1 участка i [j, j+1] определяются выражением:
T" 1 , J + 1 - T о + ( T' J - T 0 1 exp [- k n D i L i I ( MC p ) J , (14) где M i - массовый расход транспортируемого ЦП на участке i.
Из (13) и (14) можно получить выражение для средних потерь материала на участке:
T 1 - T о +
( T ' j - T 0 )
1 - exp [- k K DL, I ( M C p ) J (15) k n DLrI ( MC p ) ; ( )
Учитывая, что рассматривается система с регулируемыми параметрами, переменность потерь ЦП (как и нестационарность) приводит к необходимости организации фактически тройного цикла в алгоритме реализации модели (8)-(12). Первый (внешний) осуществляет поиск поло- жения регулирующих устройств (подсистем принятия решения) и режимов работы активных элементов. Второй (внутренний) осуществляет производственную увязку системы как объекта с сосредоточенными параметрами. Наконец, третий (внутренний) выполняет уточнение значения потерь ЦП на участках.
Модель (8)-(12) является качественно новым научным результатом формализации задач анализа потокораспределения ЦП. Она содержит в своей основе все известные до сих пор модели установившегося потокораспределения в объектах с регулируемыми параметрами.


