Модели аппроксимации данных инфракрасной термометрии

В последние десятилетия интенсивно развивается медицинская диагностика на основе комбинированной (радио- и инфракрасной) термометрии (см., например, [1]–[3]). Комбинированная термометрия – это биофизический метод неинвазивного обследования, заключающийся в измерении внутренних и поверхностных температур тканей по интенсивности их теплового излучения, соответственно, в микроволновом и инфракрасном диапазоне и последующей их регистрацией в виде числовых данных. Далее, на базе измерений в отдельных точках, строятся соответствующие множества уровня температуры, называемые термокартами, с помощью которых врач ставит диагноз. Одним из недостатков существующих термометрических методов является малое количество точек измерения и, соответственно, низкая точность аппроксимации.

В ближайшее время планируется создание принципиально нового диагностического комплекса с использованием датчиков, состоящих из нескольких сенсоров для одновременного измерения температуры в нескольких точках.

Предполагается, что инфракрасный датчик новой версии будет состоять из 7 измерителей, расположенных вдоль прямой линии на расстоянии 1 см друг от друга, при этом разрешающая способность каждого измерителя составит 1 миллиметр. Конструкцию можно будет двигать вдоль поверхности тела, измеряя значение температуры через каждый миллиметр на семи вертикальных прямых, отстоящих друг от друга на расстоянии 1 сантиметр. После этого можно будет повернуть датчик на 90o и аналогично измерить температуру на горизонтальных прямых. В результате область измерения разбивается на квадраты размером 1 × 1 см, причем будет известна температура в точках границы квадратов с интервалом 1 миллиметр. Данная работа посвящена одному методу аппроксимации температуры внутри исследуемой области, при этом предлагаемый способ позволяет достаточно точно улавливать зоны с резко изменяющейся температурой, которые являются наиболее значимыми при диагностике различных заболеваний.

Для решения этой задачи предлагаются две математические модели. В первой модели предлагается приближать температуру u ( x , y ) с помощью гармонических функций. Внутри каждого квадрата вводим сетку с узлами, расположенными через 1 мм (всего 121 узел вместе с граничными). Значения во внутренних узлах сетки находим, решая задачу Дирихле для оператора Лапласа

Г Ди = 0 R_g = ^f .

Для дискретизации задачи используется стандартная разностная схема [5]:

ui-1,j

—

^2ui,j + ^ui+1j   ^uij-1

+—

^{— 2u}i, j + ^u i, j+1 _

^—h₂       = ■

Полученную после дискретизации систему линейных уравнений решаем методом Зейделя [там же]. Для построения термокарты необходима аппроксимация температуры в произвольной (неузловой) точке квадрата, для получения этой аппроксимации проводим через узлы кубический сплайн [4].

Для апробации модели использовались результаты термометрических исследований, проведенных в течение последних нескольких лет в Волгоградском флебологическом центре профессора С.И. Ларина [2].

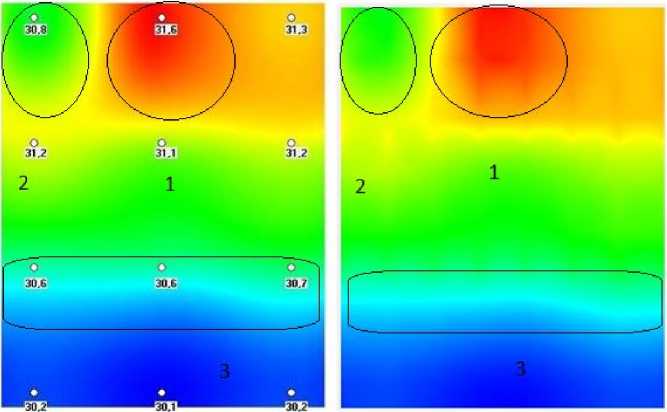
Рис. 1. Аппроксимация гармоническими функциями в случае медленно меняющейся температуры

В результате вычислительных экспериментов было показано, что данная модель адекватно отслеживает плавные изменения температуры. В качестве примера рассмотрим тепловую карту, изображенную на рисунке 1. В левой части рисунка мы видим образцовую тепловую карту, справа – приближение, полученное с помощью решения задачи Дирихле для оператора Лапласа. Легко заметить, что большие области (обведены овалами в левом верхнем углу рисунка) отображаются на модели с достаточно высокой точностью. Также адекватно улавливается граница перехода температуры (область в нижней трети рисунка). На модели (в верхней части) просматривается дополнительная решетчатая структура, которой нет на образцовой карте. По всей видимости, это неустранимые эффекты численного моделирования. Путем сравнения с образцовыми картами вычислялась погрешность аппроксимации, для тепловых карт с плавным изменением температуры она не превосходит 1,5 %, такая точность вполне достаточна для медицинских целей.

Когда температура изменяется сильно, данный способ не вполне адекватно описывает распределение температур. В качестве примера попробуем промоделировать вертикальную «вену». На рисунке 2 слева изображена образцовая карта, а справа – аппроксимация с помощью гармонических функций.

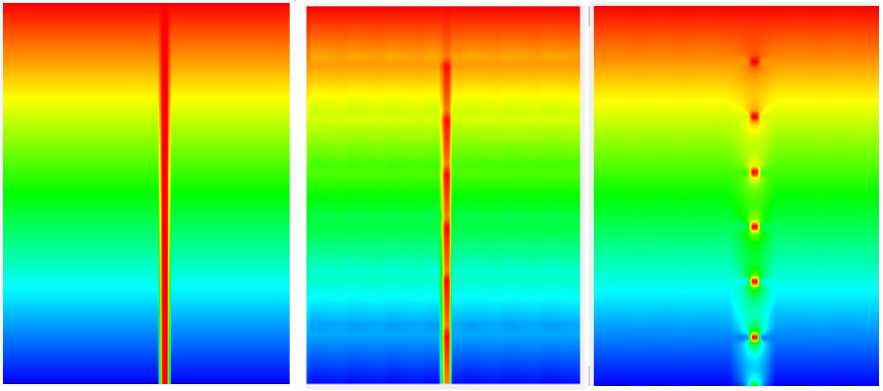
Рис. 2. Температурная карта с вертикальной «веной»

На модели видны отдельные точки вертикальной «вены», но сама она не улавливается моделью. Это связано с тем, что «вена» является сильным тепловым источником, в результате чего в уравнение Лапласа необходимо добавлять правую часть, зависящую от расположения «вены», которое нам известно лишь частично. Для моделирования ситуаций сильно меняющихся температур более подходящей аппроксимацией является приближение с помощью поверхностей Кунса (рис. 2, средняя карта).

Для построения поверхности Кунса [6] сначала кубическими сплайнами приближаются значения температуры на границах каждого квадрата, а затем температура в любой точке внутри квадрата определяется линейной интерполяцией между точками противоположных границ квадрата. В такой модели граничные условия влияют на температуру внутри квадрата сильнее, чем в модели гармонических функций.

На рисунке 3 показано сравнение двух моделей на примере карты с сильно меняющейся температурой. Левая карта – это образец, средняя – приближение с помощью поверхностей Кунса, правая – аппроксимация гармоническими функциями. Хорошо видно, что в случае быстро меняющихся температур (в левом верхнем углу карты) поверхности Кунса аппроксимируют температурные поля точнее, чем гармонические функции. Еще можно заметить, что поверхности Кунса улавливают и достаточно тонкие колебания температуры в нижней трети рисунка. В целом в случае медленно меняющихся температур поверхности Кунса чуть хуже описывают ситуацию (погрешность измерения около 2,5 %).

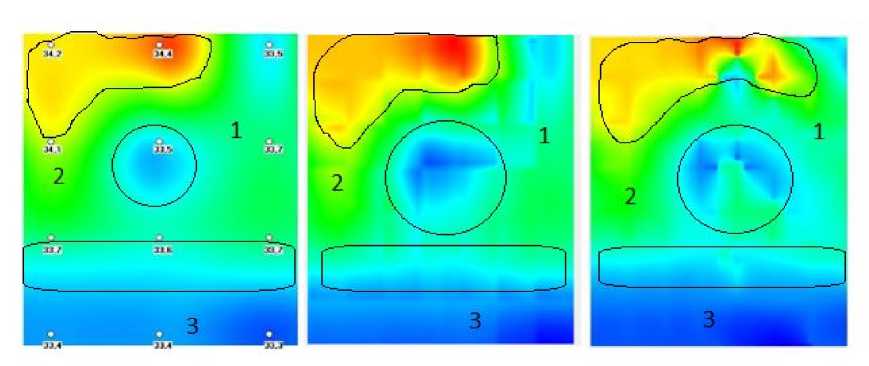
Рис. 3. Сравнение двух моделей аппроксимации

Таким образом, в случае плавного изменения температуры обе модели работают удовлетворительно, а в случае резких изменений лучше использовать приближение Кунса.