Модели динамики пылевидной материи в собственном поле тяготения

Задачи о динамике пылевой среды имеют важное значение для астрофизики и космологии. К этому классу задач относятся задачи о формировании плотных астрофизических объектов из рассеянных облаков пыли - неустойчивость Джинса (см. [1, 2] и библиографию там), а так же задачи о космологическом расширении Вселенной, в которых роль пылевидной материи выполняют скопления галактик. Задача о формировании плотных объектов, например, звезд и галактик, относится к начальным этапам этого процесса, когда давление газовой составляющей еще несравнимо меньше, чем сила тяготения, а кривизна пространства очень мала. В этом случае для анализа динамики формирования плотных объектов на ранних стадиях можно использовать классическую теорию тяготения. В космологии, наоборот, этап расширения пылевидной материи относится к временам после завершения эпохи инфляции [3]. После завершения эпохи инфляции для случая пространственно-плоской Вселенной динамика расширения Вселенной может рассматриваться в рамках не ОТО, а классической теории тяготения Ньютона. Задача о расширении однородной по плотности распределения пыли со сферической симметрией в рамках классической теории тяготения Ньютона рассматривалась в работах [4, 5]. Таким образом, модели динамики пылевидной материи вполне могут применяться для широкого круга задач астрофизики.

Стандартным подходом к решению задач динамики пылевых объектов является метод годографа [1,2,6]. Однако этот подход имеет свои ограничения и часто его решения не имеют простого наглядного смысла. В качестве альтернативного подхода для задач теоретической физики, в том числе, гидродинамики, в работах [7–10] был предложен метод обобщенных подстановок типа Коула-Хопфа [12, 13]. В отличие от метода годографа метод, основанный на обобщенных подстановках Коула-Хопфа, позволяет строить решения в более ясной с физической точки зрения форме и расширяет круг задач, для которых таким способом можно получить точные решения.

Подход, развитый в [7, 8, 10] был модифицирован специально для задач гидродинамики в работе [11], что позволило получить ряд новых точных решений для ряда гидродинамических задач [14, 15].

В настоящей работе эти результаты обобщаются и применяется к задаче построения аналитических точных решений течений самогравитирующей пыли. Эти решения анализируются по аналогии с [2] с точки зрения некоторых особенностей процесса формирования плотных сферических астрофизических объектов. Кроме этого, в работе строятся развитым методом решения задач об однородном и неоднородном сферически симметричных потоках Хаббла, играющих важную роль в современной космологии. Рассмотрены некоторые конкретные примеры.

1.    Общая схема гидродинамических подстановок

Следуя общей идеологии работ [7,8,10,14,15], рассмотрим такие течения жидкости и газа, которые сводятся к одномерным уравнениям гидродинамики, за счет, например, цилиндрической или сферической начальной симметрий. В соответствии с [15] воспользуемся методом функциональных подстановок в форме, приспособленной для задач гидродинамики. Течения жидкости или газа, сводящиеся к одномерным уравнениям гидродинамики, целиком описываются с помощью задания поля скорости среды u ( x , t ) как функции координаты и времени. Состояние среды при этом описывается ее плотностью массы ρ и заряда ρ e , если это плазма. С каждой точкой среды можно формально связать маркерную функцию 6 = 6 ( x , t ) , значения которой привязаны к точкам среды. Это означает, что уравнение для функции такого переноса можно записать в следующем виде:

6 _t + u ( x , t ) 6 x = 0.                                            (1.1)

Дифференциальным следствием этого соотношения является уравнение неразрывности:

^.Р + ^d ( u^p ) = 0, ∂ t     ∂ x

(1.2)

(1.3)

с плотностью среды p = 6x которое получается простым дифференцированием (1.1) по x. Это общее наблюдение позволяет рассмотреть специальный подход для конструирования моделей динамики среды, опирающийся на свойства функции маркера θ. Эти свойства θ описываются уравнением переноса (1.1) и следующими из него уравнениями неразрывности для плотности p = 6x, а так же другими дифференциальными тождествами. Суть метода состоит в том, чтобы используя свойства маркеров, найти подходящий вид поля скорости v (x, t) как функции от 6 и ее производных, при которой объемные силы, действующие на среду, приобретают нужную форму. Именно тип действующих сил и определяет характер модели. Такой подход существенно меняет общий взгляд на возможности анализа нелинейных по своей сути уравнений гидродинамики. Интуиция подсказывает, что попытка построить решение гидродинамической задачи с помощью какой-либо суперпозиции поля заранее обречена на провал, поскольку уравнения гидродинамики нелинейны. Однако рассматриваемый подход демонстрирует существование особого типа суперпозиции в гидро- динамике, а именно возможность разложить поле скорости на отдельные аддитивные составляющие, отвечающие за различающиеся по физической сущности объемные силы, которые, как правило, обладают свойством суперпозиции в соответствии с большинством физических зако-

нов теорий тяготения Ньютона и электродинамики.

В качестве простого примера рассмотрим еще одно формальное тождество (кроме (1.2)), которое получается из уравнения переноса маркера. Дифференцируя уравнение неразрывности

(1.2), находим:

∂

∂

d t^{6х +} u d x ^6х = u x ⁶ x ,

(1.4)

или

— In 6 x + u — In 6 x = — U x .

(1.5)

Важным является то, что эти тождества выглядят как результат действия оператора переноса:

∂∂

L = d t ⁺ v ⁽ x • t ⁾ d x

(1.6)

на некоторые функции, связанные с функцией маркеров 6 ( x , t ) .

В качестве примера рассмотрим поле скорости вида:

u(x, t) = qIn6x + U(6), q — const.

Тогда в силу тождества (1.5) и уравнения переноса маркера (1.1), находим, что такое поле скорости удовлетворяет уравнению:

f                         2 d ln 6 x

L u — Ut + uux — — Ux — - q —dx— — - -d- ’(1-8)

если функция θ удовлетворяет уравнению:

6t + (q ln 6x + U (6)) 6x — 0.

Уравнение (1.8) представляет собой уравнение Эйлера для изотермического течения газа с q ² — RT I ц , где T - абсолютная температура, R - универсальная газовая постоянная, ц - молярная масса газа.

Уравнение (1.9) интегрируется просто в случае U ( 6 ) — U ₀ — const [16,17]. При этом условии, после дифференцирования уравнения по x , оно приводится к уравнению Хопфа:

pt + (q ln p + Uо + q) px — 0, которое имеет общий интеграл:

H (p, x — F (p) t) — 0, где F(p) — qInp + U0 + q, а H(p, £) — произвольная дифференцируемая по обоим аргументам функция. Ограничение на вид функции U(6) приводит к ограничению на возможность одновременно задавать начальные распределения и плотности, и скорости потока. При сделанном предположении U(6) — U0 — const, начальное распределение скорости почти целиком (за исключением постоянной U0) определяется распределением плотности в силу использованной подстановки (1.7):

u ( x , 0) — q ln p ( x , 0) + U ₀ + q .

Этот пример демонстрирует основные идеи использования подстановок для поля скорости, основанные на тождествах, вытекающих из уравнения переноса маркеров.

2.    Течения самогравитирующей пыли. Общая формулировка задачи

Развитый метод, который в дальнейшем мы будем называть гидродинамическими подстановками , можно использовать для решения более широкого круга задач, в частности, для решения задач динамики самогравитирующей пыли. Метод был предложен в работе [15]. В этом случае к уравнениям гидродинамики необходимо добавить уравнение Пуассона для потенциала поля тяготения, созданного самой пылью. Самосогласованная система уравнений имеет следующий вид:

u_t + uu x

— Ф x , p t + -^{1 d} ( x n u p 1 — 0, xⁿ ∂ x

(2.1)

(2.2)

"1 ^d ( x n Ф x 1 — ⁴ n G p . xⁿ ∂ x

Уравнения (2.1) – уравнения Эйлера, уравнение (2.2) – уравнение Пуассона. Уравнение состояния пыли эквивалентно требованию равенству давления нулю, поэтому силы Архимеда в данной системе нет. Здесь ф ( x , t ) - потенциал гравитационного поля, G - постоянная тяготения Ньютона, а целое число n — 0,1,2 - соответствует координатной размерности задачи d — n + 1 . В случае n — 1 - задача с цилиндрической симметрией, а в случае с n — 2 - сферической.

Физическая постановка задач, связанных с системой (2.1)–(2.2), состоит в описании процесса формирования плотных компактных объектов из рассеянных скоплений пыли под действием собственного поля тяготения. Поскольку процесс формирования плотных объектов из пыли происходит без силы Архимеда, то он практически всегда [2] заканчивается образованием сингулярности в распределении плотности. Одним из основных параметров этого процесса является время образования сингулярности из начального состояния. Для решения этих задач воспользуемся методом гидродинамических подстановок.

3.    Задача с плоской симметрией

Построение решения этих задач начнем со случая n = 0 . Подставляя (1.3) в (2.2) и затем интегрируя по x , получаем уравнение следующего вида:

ф х — g о ( t ) + 4 n G 0 .

(3.1)

Здесь g ₀ ( t ) - постоянная интегрирования по х, характеризующая фактически ускорение системы отсчета. Подставляя это соотношение в первое уравнение (2.1), преобразуем его к следующему виду:

u t + uu_x — - 4 n G 0 - g ₀ ( t ).                                 (3.2)

Суть этого соотношения состоит в том, что гидродинамическим маркером одномерного само-гравитирующего течения пыли является ускорение свободного падения g — ф _x . Это означает, что все точки пыли сохраняют при своем движении ту величину ускорения свободного падения, которое существовало в начальный момент времени. Этот результат, кажущийся достаточно случайным, является, на самом деле, общим свойством самогравитирующих структур без давления. Обобщение этого вывода мы рассмотрим далее.

Решение для поля скорости будем искать в следующем общем виде:

u ( x , t ) = U ( 0 ) + h ( t ) 0 + v о ( t ).                                     (3.3)

Действуя на эту функцию оператором переноса L , находим:

L u — 0 h + v ₀ ( t ).

Сравнивая это соотношение с (3.2), получаем:

h ( t ) =- 4 n Gt + h ₀ , v ₀ = - g ₀ ( t ).                                 (3.4)

Таким образом, решения исходной системы уравнений строятся, исходя из решений уравнения для маркера следующего вида:

0 t + ( u ( 0 ) + ( - 4 n Gt + h 0 ) 0 + v 0 ( t ) j 0 _x — 0.

(3.5)

(3.6)

Это уравнение имеет неявное решение:

0 — H ( x - U ( 0 ) t + (2 n Gt ² - h 0 1 ) 0 - x 0 ( t ) j .

Здесь H ( 5 ) - произвольная дифференцируемая функция аргумента:

x ₀ ( t ) — / v ₀ ( t ) dt .

ц — х - U ( 0 ) t + (2 n Gt² - h 0 1 ) 0 - x 0 ( t ),

Функция H ( ^ ) определяется начальным распределением маркера в пространстве:

0 (x ,0) — H(x - x0(0)], которое связано с начальным распределением массы:

р ( x ,0) — 0 x 1 1 —0 — H ‘ ( x - x 0 (0)].

Начальное распределение скорости задается функцией U ( 0 ) :

u ( x ,0) — U (0 ( x ,0)] + h ₀ 0 ( x ,0) + v ₀ (0).

Заметим, что масса среды, сосредоточенная в интервале координат [ x 1 , x ₂ ] , определяется разностью значений маркера:

x 2

M [ x i , x 2 ] ( t )

J” 0 _xdx — 0 ( x ₂ , t ) - 0 ( x 1 , t ).

(3.7)

x 1

Важной характеристикой распределения масс является полная масса среды:

M о = 9 ( то , t ) - 9 ( -то , t ) •

Для астрофизических приложений необходимо рассматривать такие распределения массы в пространстве, для которых полная масса пыли должна оставаться конечной и постоянной во времени в случае бесконечного интервала [ x ₁ , x ₂ ] . Последнее условие означает, что нет самопроизвольного притока или оттока массы в систему, что обеспечивается в силу выполнения уравнения неразрывности нулевыми значениями скорости потока на бесконечности: и ( то , t ) = и ( -то , t ) = 0 . Отсутствие среднего перемещения центра масс всей системы в пространстве должно соответствовать условию:

то

то

V о =

ddjx^р dx ^_/

x р _tdx =

-то

-то

то

то

- j x д - (и р ) dx _ j и ( x , t ) р dx _ 0.

-то

-то

(3.8)

Одним из общих явлений, наблюдаемых в самогравитирующих системах [1, 2], является возникновение сингулярностей в распределении массы за конечное время. Момент образования сингулярности определяется, как и в случае определения момента опрокидывания простой волны, первым моментом появления точки ( x * , t * ) , в которой плотность обращается в бесконечность: р ( x * , t * ) = то . Этот момент определяется с помощью вычисления производной 9 x из общего решения (3.6). Имеем:

9 x = H '( 5 )(1 - U '( 9 ) 9 x + (2 n Gt ² - h о t ) 9 x )•

Отсюда находим:

_ _е ________ W)_______

(3.9)

^{р x} 1 + H ‘ ( $ )[ U ‘ ( 9 ) - (2 n Gt ² - h о t )]•

Первый момент образования сингулярности определяется из условия, что знаменатель этого соотношения обращается в ноль. Для иллюстрации выводов общего анализа приведем несколько примеров.

Наиболее простой случай соответствует классической задаче Джинса, когда начальное распределение плотности и скорости однородны: р ( x ,0) = р ₀ = const, и ( x ,0) = 0 . Выбор однородного значения скорости, равного нулю, лишь фиксирует выбор определенной системы отсчета. Однородное же распределение массы соответствует бесконечной суммарной массе на бесконечном пространственном интервале. При таких начальных условиях имеем:

U(9) = 0, 9(x,0) = ax + 90, H(5) = а^ + 90 + x0(0), где а и 90 - вещественные постоянные. В этом случае решение имеет следующий вид:

9 _ a(x + (2 n Gt ² - h 0 1 ) 9 - x 0 ( t ) j + 9 0 + x 0 (0)•

Отсюда находим:

9 _ a ( x - x 0 ( t )) + x 0 (0) + 9 0

1 - 2 n Gt ² + h 0 1

Это решение демонстрирует конечный результат эволюции однородного распределения плотности. Оставаясь со временем однородным распределением, плотность за конечное время t * _ 1Л/2 n G в каждой точке пространства одновременно обращается в бесконечность. Этот результат можно рассматривать как вариант парадокса Зеелигера для плоско-симметричного распределения материи.

Более физически значимый пример можно получить, рассматривая начальные распределения следующего вида:

р ( x ,0) _ , ^р 0, ₉ , и ( x ,0) _ 0,                                  (3.10)

1 + x ² / a ²

где a _ const - параметр, характеризующий ширину начального распределения Лоренца. Масса такого распределений конечна:

то dx

_ пр о a •

M 0 ^_ р 0 I ----

J 1 + x ² / a ²

-то

Функция H ( 5 ) при таком начальном распределении имеет вид:

x

0 ( x ,0) = H ( x - x о (О))

j р ( y ,0) dy = р ₀ a arctg( x I a ). -TO

Начальное распределение скорости выберем, как и в простейшем случае, однородным с нулевым значением во всем пространстве. В силу этого U ( 0 ) = 0 . Решение для 0 теперь находится из решения уравнения:

0 = р ₀ a arctg[( x + 2 n Gt ² 0 )I a ].

Здесь полагалось x ₀ ( t ) = 0 и h ₀ = 0 . После отыскания решения для 0 , решения для р ( x , t ) и u ( x , t ) вычисляются с помощью соотношений:

р ( x , t ) =

_____________£ 0_____________

1 + ( x + 2 n Gt ² 0 ) I a ² - р ₀ 2 n G t ²

u ( x , t ) = - t 0 ( x , t ) = - t р ₀ a • arctg[( x + 2 n Gt ² 0 )I a ].

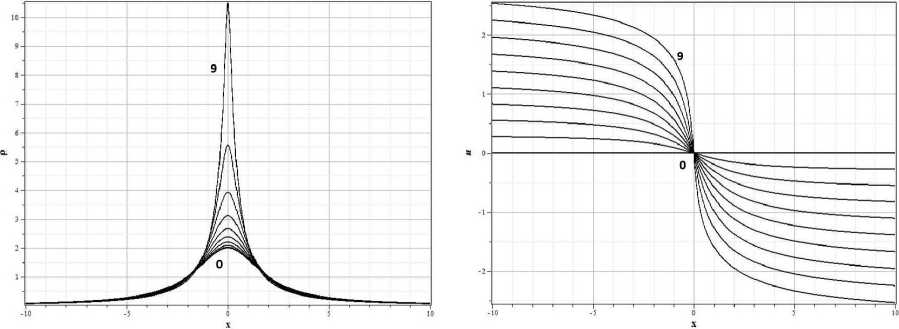
Графики плотности и скорости потока для нескольких значений времени t приведены на рисунке 1. Графики построены вплоть до момента времени t * = V2, когда происходит образование сингулярности. Масштабы времени и плотности выбраны равными соответственно: 2 n G = 1, a = 1, р ₀ = 0 .

ab

Рис. 1. Эволюция плотности (a) и скорости потока (b) для начальных распределений (3.11), 0 - t = 0, 9 - t = 0.9 (с шагом Д t = 0.1).

Еще один пример построения решения для системы с плоской симметрией приведен на рисунке 2. Этот пример соответствует начальному распределению плотности в виде двух локальных флуктуаций:

^{р (} x ^,0)    1 + ( x ^ b ) ² I a ^{2 +} 1 + ( x ^ b ) ² I a ² , u ⁽ x ^,0) 0’

(3.11)

для следующих значений параметров: a = 1, b = 1, р ₀ п = 1 . Соответствующее выражение для начального распределения маркера имеет следующий вид:

0 ( x ,0) = H ( x - x ₀ (0)) = р ₀ a ^arctg(( x - b )I a ) + arctg(( x + b )I a )j.

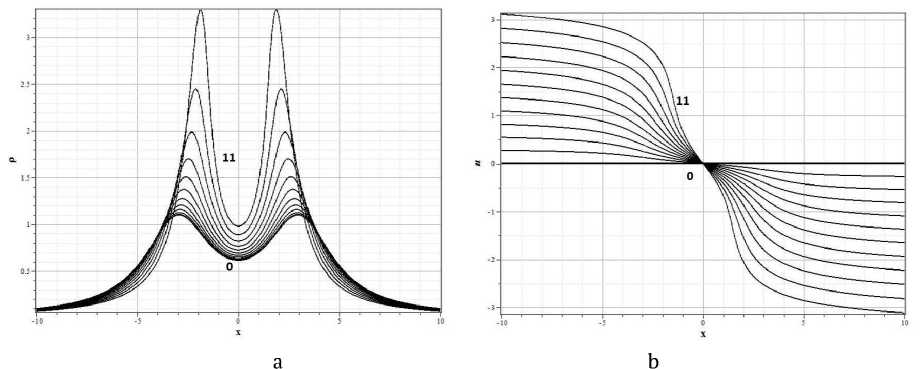
Рис. 2. Эволюция плотности (а) и скорости потока (b) для начальных распределений (3.11), 0 - t = 0, 11 - t = 1.1 (с шагом Д t = 0.1).

4.    Задачи с цилиндрическим и сферическим фронтами

Для реализации развитого подхода к интегрированию системы (2.1) в случае цилиндрической n = 1 и сферической симметрий n = 2 необходимо ввести замену переменных и несколько преобразовать уравнения. Одновременно получим и другое решение задачи с плоским фронтом на полупрямой. Вместо плотности введем новую функцию R = xⁿ р . В этом случае уравнения с функцией R будут иметь такой вид:

u_t + uu_x

— I

ф х , R t + д ( Ru j = 0,

^д~ ( x n ф х 1 = 4 n GR . ∂ x

Для системы такого вида связь маркера θ с плотностью будет определяться следующим соотношением:

R = 9 х = x n р .

При этом уравнение неразрывности получается автоматически как и в одномерном случае. Интегрируя уравнение Пуассона, находим:

ф х = x n ( 4 n G⁶ + g o ( t ) ) .

(4.1)

Подставляя это выражение в уравнение для радиальной скорости u ( х , t ) , приводим его к следующему виду:

U t + uu x = — — (4 n G 6 + g o ( t )].                              (4.2)

Для простоты будем полагать, что g ₀ ( t ) = g ₀ = const .

Соотношение (4.1) представляет собой обобщение соотношения (3.1) и показывает, что в случае цилиндрической и сферической симметрий маркером является ускорение свободного падения, умноженное на якобиан преобразования от декартовых координат, соответственно, к цилиндрическим ( n = 1 ) и сферическим ( n = 2 ). Это указывает на то, что этот факт не является случайным и отражает общее свойство гравитационного поля.

Гидродинамическую подстановку для u будем искать в следующем виде:

u = f ( х ) F ( 6 ).

(4.3)

Действуя на это соотношение оператором L , получаем:

L u = uf '( х ) F ( 6 ) = f ( х ) f ‘ ( х ) F ² ( 6 ).

Сравнивая правую часть этого выражения с (4.2), находим условия, при которых они будут совпадать. Первое условие состоит в уравнении:

f ( x ) f '( x ) = - xn.                                       (4.4)

В этом случае вторым условием является алгебраическое уравнение для функции F ( 6 ) :

F ² = (4 n G 6 + g о ).                                       (4.5)

Для функции f ( x ) получаем следующие решения:

	V 2 V a ~ x ,	n = 0;
f n ( x ) = ^	V 2\/ln( a / x ),	n = 1;	(4.6)
	V 2 V a — 1 + x —1 ,	n = 2.

Здесь a - постоянная интегрирования. Соответственно, вычисляем решение для функции F ( 6 ) :

F ( 6 ) = е ^ 4 n G 6 + g о .

(4.7)

Здесь е = ± 1 .

После того, как определены все функции подстановки (4.3), можем выписать уравнение для θ , которое теперь будет иметь следующий вид:

6 t + F ( 6 ) f_n ( x ) 6 x = 0.                                       (4.8)

Это уравнение заменой переменных приводится к уравнению Хопфа:

6 t + F ( 6 ) 6 z_n = 0,

(4.9)

где

Z n ( x ) = *

—~ V a — x , ^2

x

a V 2 J” e y ² dy + z ₀ ,

—( a In ( x + V x ² + ax + a /2 ^ + 2 V x ² + ax j , 2 2 a

n = 0;

n = 1;

n = 2.

Общий интеграл этого уравнения имеет вид:

6 = H^Z n ( x ) — F ( 6 ) t ).

(4.10)

Распределение массы вычисляется из соотношения:

6 x = z'n ( x )       H ' ( 5 )

xⁿ xⁿ 1 + H ‘ ( $ ) F ‘ ( 6 ) t ■

(4.11)

Здесь 5 = z_n ( x ) — F ( 6 ) t . Расчет массы в пространстве производится теперь с помощью следующих соотношений:

x 2

x 2

M x 1 , x ₂ = 2 ⁿ nJ p ( x ) xⁿdx = 2 ⁿ nJ 6 x ( x ) dx = 2 ⁿ n ( 6 ( x ₂ , t ) — 6 ( x 1 , t ) j .             (4.12)

x 1

x 1

Отсюда следует, что в двумерном и трехмерном варианте модели масса, содержащаяся в интервале радиальных координат, определяется разностью значений маркеров.

Начальное распределение маркера связано с функцией H ( ^ ) , которая вычисляется из соотношения:

6 ( x ,0) = H ( Z n ( x )).

(4.13)

Соответственно начальное распределение плотности массы и скорости можно вычислить из соотношений:

z„ ( x )

R ( x ,0) = ^—H '( z n ( x )), u ( x ,0) = f n ( x ) F\H ( Z n ( x )) .                   (4.14)

xn

Наличие произвольного знака перед функцией F ( 6 ) означает, что при одном и том же начальном распределении плотности имеются два различных начальных распределения скорости, для которых решения будут описываться соотношениями (4.10) и (4.11). Поскольку функция F ( 6 ) является фиксированной, то данное решение не является полным, поскольку начальное распределение скорости задается начальным распределением массы. Однако даже в такой ограниченной форме задача важна для астрофизики [1, 2].

Рассмотрим в качестве примера начальное распределение маркера в форме, аналогичной для плоской симметрии (3.11):

6 = р o arctg [ ( z 2 ( x ) - z ₂ (0)) ⁶j .                                   (4.15)

Динамика рассчитывается для двух вариантов параметра a , входящего в определение функции z ₂ ( x ) . Первый соответствует значению a = 0 , что дает для функции z ₂ ( x ) следующее выражение:

z ₂ ( x ) = 2 V2 x .

Этому значению a соответствует начальное распределение плотности следующего вида:

р ( x ,0) = 1536/(65536 x ⁶ + 1).

Второй вариант соответствует выбору a = 1 . Для этого значения имеем соответственно:

z 2( x ,2) = ln ( x + 1 + V x ² + 2 x )/2 + V x ² + 2 x /2;

6 f , ( x )     [ z 2 ( x )] ⁵

^{р (} x ^,0) =    x ²    1 + [ z 2 ( x )] ¹² /4 ^.

(4.16)

(4.17)

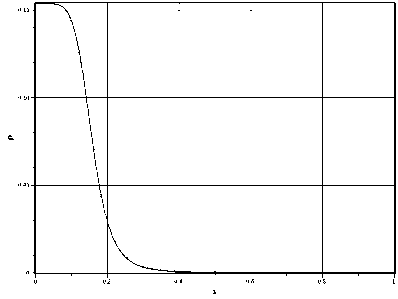
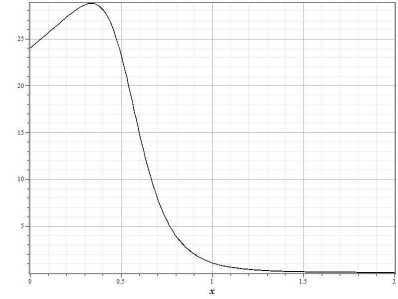
Выбор такого распределения обеспечивает несингулярное распределение плотности в нуле. Графики начальных распределений плотности представлены на рисунке 3.

a

Рис. 3. Начальное распределение плотности для вариантов a = 0, g = 0 (a) и a = 2, g = 3 (b).

b

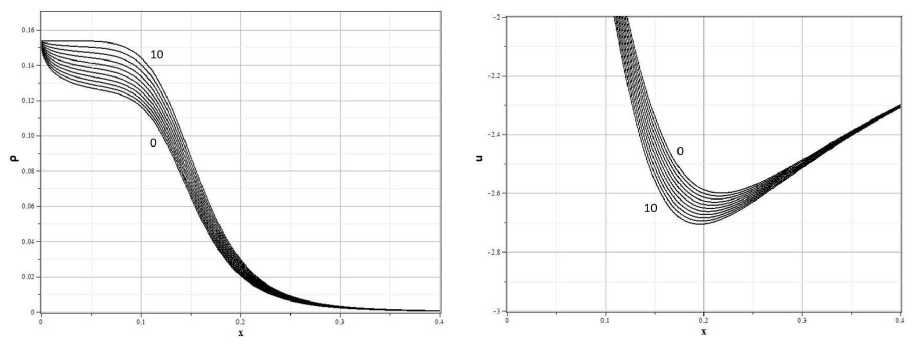
Вариант распределения на рисунке 3a соответствует возмущению с максимумом плотности в нуле, а вариант на рисунке 3b – с максимумом на некотором расстоянии от центра. На рисунках 4 и 5 представлены графики, демонстрирующие эволюцию начальных распределений плотности (a) и поля скорости (b) со временем до образования сингулярности в центре. Для обоих типов распределений плотность убывает на бесконечности, а скорость потока либо также стремится к нулю, если a = 0 , либо к постоянному значению при a = 0 .

a

b

Рис. 4. Эволюция плотности (a) и скорости потока (b) для начальных распределений (4.17), вариант a = 0,g = 0, 0 - t = 0, 10 - t = 0.04 (с шагом Д t = 0.004).

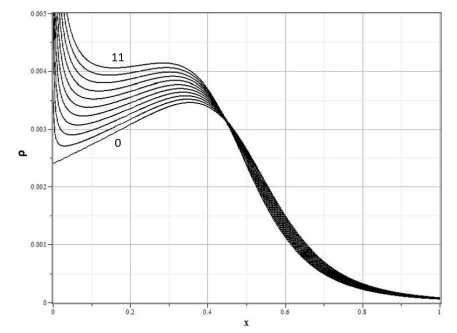
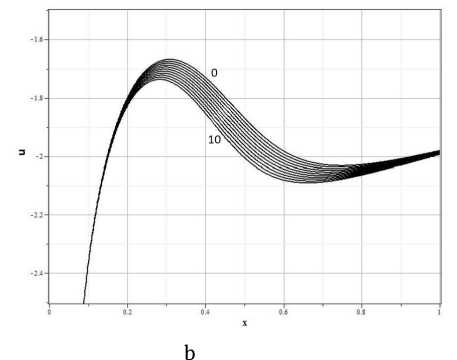
Рис. 5. Эволюция плотности (a) и скорости потока (b) для начальных распределений (4.17), вариант a = 2, g = 3, 0 - t = 0, 10 - t = 0.04 (с шагом Д t = 0.004).

5.    Однородный поток Хаббла

С помощью развитого метода среди интегрируемых задач интерес представляет задача о космологическом расширении в случае пространственно-плоской Вселенной в рамках классической механики [4, 5]. Для построения соответствующего решения рассмотрим в сферическом случае подстановку для поля скорости следующего вида:

u(x, t) = H(t)x, где H(t) - некоторая функция времени. Соотношение (5.1) представляет собой закон Хаббла космологического расширения [3,5], в котором функция H(t) называется параметром Хаббла. Вычисляя действие оператора L на u(x, t), находим:

Lu = ut + uux = Hx + H (t) u = (11 + H2) x.

Используя (5.1), для маркера получаем уравнение:

et + h (t) xex = 0.

Решение этого уравнения имеет следующий общий вид:

e = T^xI a(t)], где T(5) - произвольная дифференцируемая функция, a(t) - функция, называемая в космологии масштабным фактором:

H ( t ) = t il a .

Отсюда находим распределение плотности среды в пространстве:

р ^_ x 2 " ■ ^_ — ^{T ,( x 1} a '•                           ⁽5.⁵⁾

С другой стороны, ускорение свободного падения имеет следующий вид:

ф _х = 4 n G^ T ( x l a ).                                  (5.6)

Для того, чтобы это выражение совпадало с правой частью уравнения Эйлера (5.2), достаточно выбрать функцию T ( x l a ) в следующем виде:

T ( 5 ) = a^ ³ .

В результате, находим:

x ut + uux _ (H + H )x _ -4nG—a.

Из этого соотношения находим уравнение для масштабного фактора:

H i + H

_r2 _ 4 n G a

a ³

.

Распределение плотности в пространстве в этом случае однородно и имеет вид:

_ 3 a ^р = "m ■

(5.7)

(5.8)

Отсюда видно, что постоянная 4 na представляет собой массу материи внутри сферы радиуса a ( t ) , которая остается постоянной в процессе расширения ( H >  0 ) или сжатия H <  0 пыли.

Уравнение (5.9) можно переписать в стандартной форме относительно масштабного факто- ра:

4 n G a

(5.9)

a_    5“ a2

что соответствует классической модели космологического расширения [3]. Это уравнение интегрируется в квадратурах. Именно, первый интеграл движения для (5.9) имеет такой вид:

a ²

— _ E +

4 n G a

.

a

(5.10)

Здесь E – постоянная интегрирования. В результате, решение можно записать в виде неявной функции:

2 V EVa ( a + E ) + ln(2 V E ) - ln(2 Ea + ц + 2 V EVa ( a + E )) _ 2 E ^3/2( t - T ),        (5.11)

где T - вторая постоянная интегрирования, а ц _ 4 n G a . Построенное решение по своей сути эквивалентно классическим решениям, рассмотренным в [4, 5], но с тем отличием, что оно относится не к сфере конечного радиуса, заполненной пылью, а сразу ко всему пространству. Это делает данный подход более физически понятным.

6.    Неоднородный поток Хаббла

Рассмотрим теперь обобщение задачи Хаббла, предполагая, что параметр Хаббла может зависеть от точки среды, то есть для каждой отдельной галактики он может иметь в текущий момент свое собственное значение. Это означает, что в момент начального “взрыва” каждая из галактик могла получить свой собственный импульс в зависимости, например, от ее массы или удаления от начальной точки взрыва. Такое предположение представляется более правдоподобным, чем предположение для случая однородного потока Хаббла, в котором начальные скорости в начальный момент определяются исключительно расстоянием от центра “взрыва”.

Для реализации такой идеи вместо (5.1) рассмотрим поток следующего вида:

u ( x , t ) = H ( t , 6 ) x ,

(6.1)

где H ( t , 6 ) - параметр Хаббла, зависящий от значения маркера 6 неопределенным пока способом. Вычисляя действие оператора L на u ( x , t ) , находим:

Lu = ut + uux = THx + H (t) u = HH + H 2j x, здесь и далее HI - частная производная по t. Используя (6.1), для маркера получаем следующее уравнение:

6t + H (t, 6) x 6x = 0.

Это уравнение, как и раньше, преобразуется к уравнению Хопфа и, следовательно, его общее решение можно записать в виде:

x

6 = 0(X)- % _ —.<6.4> с произвольной функцией 0(%), где

A ( t , 6 ) = exp

(/

C

H ( t , 6 ) dt

(6.5)

где интеграл берется по времени t вдоль характеристик C , на которых θ постоянно.

Для того, чтобы неоднородный поток Хаббла соответствовал бы потенциалу поля тяготения, должно выполняться соотношение:

4nG „          ( • фx = -x2“6(x, t) = - H + H2jx.

(6.6)

Как и в случае однородного потока Хаббла для того, чтобы это уравнение разрешалось, достаточно, произвольную пока функцию 0 ( % ) выбрать следующим образом:

0 = а% ³ .

В результате, для функции H ( t , 6 ) получаем следующее уравнение:

H + H ² =

4 n G а

A ³

(6.7)

Поскольку в это уравнение функция θ не входит явно, то это уравнение можно решать так же, как и в случае однородного потока, но постоянные интегрирования по времени при этом могут быть произвольными функциями 6 . Следовательно, решение для A ( t , 6 ) будет иметь тот же вид, что и (5.11), но с тем отличием, что в нем следует считать постоянные E и T произвольными функциями 6 : E = E ( 6 ) и T = T ( 6 ) .

В отличие от однородного потока теперь распределение плотности материи (галактик) в пространстве и времени будет неоднородным и его следует вычислять, исходя из уравнения:

_ 6 x _     3 а A

^Р  x ²    A ⁴+ 3 a x ³ A₆ ’

_л dA ( t , 6 )

A^{6 _} ""дёТ

(6.8)

Это распределение зависит от выбранной зависимости решения A ( t , 6 ) уравнения (6.7) от 6 .В это соотношение следует подставлять решение из (5.11) с заданными из начальных условий значениями функций E ( 6 ) И T ( 6 ) . Смысл полученного решения состоит в том, что в случае неоднородного закона Хаббла в некоторый момент времени можно каждой отдельной галактике приписать определенную скорость космологического “разбегания” относительно наблюдателя. После этого, можно построить модель того, как Вселенная будет расширяться далее.

Полный анализ возможных космологических решений, соответствующих (6.8), выходит за рамки данной статьи. Сделаем лишь некоторые общие замечания, вытекающие из общих свойств функции р . Если A ( t , 6 ) , как функция x , ограничена при x ^^ ,тов этом пределе плотность стремится к нулю. Отсюда следует, что плотность на больших масштабах может быть нулевой, то есть распределение материи в такой модели носит островной характер. Плотность же на малых расстояниях от наблюдателя, когда x ^ 0 , будет примерно такой же, что и в случае однородного потока Хаббла.

Заключение

В работе рассмотрен метод гидродинамических подстановок для задач динамики самограви-тирующей пыли в рамках классической теории тяготения Ньютона. Найдены и частично исследованы точные решения задач динамики локальных возмущений с плоской, цилиндрической и сферической симметриями их начальных возмущений. Приведены конкретные примеры. С помощью полученных соотношений можно вычислять такие характеристики процессов эволюции возмущений, как время формирования сингулярности из начального несингулярного профиля, а также конкретный вид распределений плотности пыли и потока скорости. Решения, построенные для случая цилиндрической и сферической симметрий, не являются полными, поскольку они строятся для произвольного распределения плотности, но при этом распределение скорости потока задается распределением плотности. Однако и в этом ограниченном варианте полученные решения являются полезными для задач астрофизики.

С помощью метода гидродинамических подстановок, кроме задач эволюции локальных возмущений, в работе получено решение классической задачи об эволюции космологического потока Хаббла однородного распределения пыли в плоском пространстве пыли. На основе этого подхода получено более общее точное решение о неоднородном потоке Хаббла. Это новое точное решение может быть использовано для построения космологических моделей со сферически симметричными возмущениями плотности среды.

Работа выполнена при поддержке Министерства Образования и Науки РФ (в рамках Государственного задания и проекта № 14.Z50.31.0015), средств проекта РФФИ 16-42-732119 р_офи_м, а также за счет средств субсидии, выделенной в рамках государственной поддержки Казанского (Приволжского) федерального университета в целях повышения его конкурентоспособности среди ведущих мировых научно-образовательных центров.