Модели и алгоритмы эффективной эвакуации населения речных долин и пойм при наводнении

DOI:

В то время как чрезвычайные ситуации (ЧС) пожаров проработаны весьма детально — разработано и исследовано большое число математических, физических, химических процессов их развития, а также математических и психологических моделей поведения людей при эвакуации из горящих зданий [1], чрезвычайные ситуации наводнений исследованы значительно в меньшей степени. Возможно, главной причиной недостатка детально проработанных руководств по обеспечению гидрологической безопасности населения при наводнениях является высокий уровень и разнообразие видов неопределенностей, свойственных этому виду ЧС. Действительно, существенными факторами гидрологической безопасности населения затапливаемых территорий являются параметры чрезвычайного речного гидрографа Q(t), территориальная динамика распространения вод, моменты получения населением информации о наводнении, общее число эвакуирующихся жителей и их распределение по населенным пунктам (НП), выбираемый ими способ и эвакуационные маршруты (ЭМ) — организованная эвакуация эвакуационными транспортными средствами (ЭТС) или самостоятельная эвакуация личным транспортом, места расположения эвакуационных пунктов (ЭП), динамика выезда населения из НП, число имеющихся в распоряжении ЭТС организованной эвакуации, моменты начала эвакуации. Числовые характеристики всех факторов обладают неопределенностью. Однако эта неопределенность может быть значительно снижена заблаговременным исследованием математических и геоинформационных моделей развития наводнений, поведения населения и организации эффективного управления ЧС для конкретных территорий, возможность создания которых стала реальной в связи с развитием технологий параллельных вычислений. Эти модели могут служить эффективным инструментом управления безопасным развитием территорий также в среднесрочной (управление проектами гидрологической безопасности) и долгосрочной (управление территориальной социально-экономической структурой) перспективе. Особенности природной и социально-экономической структуры территорий существенно влияют на характеристики их систем гидрологической безопасности. Так, например, наводнения в речной долине равнинной р. Амур по внезапности возникновения и быстроте распространения существенно отличаются от наводнений на равнинных реках и подобны наводнениям в горной местности вследствие того, что причинами наводнений являются дожди или бурное снеготаяние в бассейнах ее притоков, протекающих в гористой местности. Другим примером является наличие или отсутствие проблемы эвакуационного транспортного коллапса в городах и сельской местности.

В связи с развитием в последние десятилетия технологий высокопроизводительных вычислений и ГИС-технологий проблема организации эвакуации населения при наводнении привлекает к себе большое внимание исследователей. Комплексная неопределенность этой проблемы является причиной разнообразия создаваемых моделей управления эвакуацией населения. Среди критериев эффективности встречаются, например, минимизация времени эвакуации, максимизация численности эвакуированного населения [6; 12], минимизация ущерба [7; 10], затрат на организацию эвакуации и помощи населению [14], оптимальное расположение мест укрытий [14], мест отдыха [18], максимизация комплексного критерия безопасности [8]. В составе методов решения задач управления используются модели динамики наводнений [4; 6], модели дорожной сети и транспортных потоков [8; 12], теоретико-игровые [3; 6; 11], сценарные [3; 7; 10; 12], многоагентные [2; 6; 7], эконометрические [10], динамические [6; 8], стохастические [6] модели, целочисленное и линейное программирование [14; 18], эвристические методы оптимизации и принятия решений [6; 11; 14; 18]. Однако задачам оптимизации расписаний организованной эвакуации не уделено достаточного внимания.

Объектами нашего исследования являются наводнения на территориях речных долин и пойм крупных равнинных рек. Природные условия пойм зарегулированных крупных рек являются особенно благоприятными для социохозяйственного освоения. Однако превышение предельных безопасных значений речного гидрографа в период весенних половодий или техногенный аварийный сброс большого объема вод через плотины ГЭС представляют серьезную опасность для многочисленного населения этих территорий вследствие их низменного рельефа, высокой территориальной распределенности населения и невысокой густоты дорожной сети. Особенностью территориального распределения пойменных НП и рельефа их дорожной сети является более раннее затопление значительной части ЭМ, чем самих НП. Поэтому эвакуация населения пойм в условиях дефицита времени может характеризоваться высоким уровнем гидрологического и транспортного рисков. Отсутствие детальных руководств по формированию адаптивных расписаний организованной эвакуации населения во время наводнений, учитывающих свойства рельефа, пространственного распределения населения и дорожной сети конкретных территорий, создает дополнительную потенциальную опасность. Использование двух популярных критериев эффективности эвакуационных расписаний — общего времени эвакуации (минимизация) и общего количества эвакуированного населения (максимизация) на территориях речных долин и пойм приводит к неоправданному завышению необходимого числа ЭТС и, соответственно, к неопределенности расписания при отсутствии этого количества. Это обстоятельство обусловливает актуальность создания и исследования математических моделей управления эвакуацией населения конкретных территорий (или классов территорий) с учетом особенностей динамики их затопления, расположения НП и ЭП, топологии дорожной сети, количества имеющихся у населения личных транспортных средств.

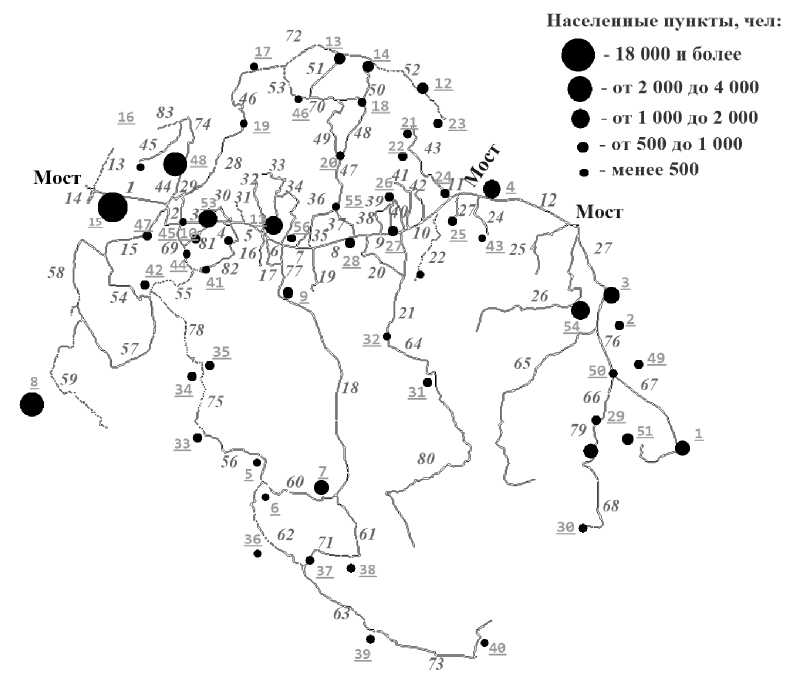
Рис. 1. Дорожная сеть ВАП с указанием расположения населенных пунктов. Цифрами обозначены номера дорог ( курсив ) и НП ( прямой подчеркнутый шрифт )

В статье предложен ряд моделей и алгоритмов построения эффективных расписаний организованной эвакуации населения при наводнениях на основе геоинформацион-ной многослойной модели территории и гидродинамической численной модели развития наводнений. Основным критерием оптимизации выступает агрегированный гидрологи- ческий жизненный риск, определяемый как суммарное время, проведенное жителями на затопленной территории. Здесь мы не исследуем проблемы самостоятельной эвакуации и выбора ЭМ, считая плотность соответствующего транспортного потока докритической, а маршруты организованной эвакуации — заданными, соответствующими минимальным расстояниям между НП и ЭП. Эти предположения обусловлены низкой плотностью и высокой территориальной распределенностью населения, а также низкой густотой дорожной сети территорий речных долин и пойм.

В качестве объекта для численной реализации предложенных алгоритмов выступает территория северной части Волго-Ахтубинской поймы (далее — ВАП). ВАП расположена в нижнем течении р. Волги в междуречье рек Волги и Ахтубы. Гидрологический режим ВАП определяется гидрографом Волжской ГЭС (ВГЭС). Развитие в последние десятилетия в ВАП федеральной дорожной сети стало мощным стимулом ее социально-экономического развития и роста населения. В настоящее время в ВАП расположено 56 населенных пунктов с общей численностью населения более 35 000. Карта дорожной сети ВАП с указанием номеров ее локальных участков и НП приведена на рисунке 1.

1.    Методы решения задачи

В результате геоинформационного и численного гидродинамического моделирования затоплений наводнений с набором чрезвычайных речных гидрографов Q = Q(t) конкретной территории речной долины (поймы) при помощи вычислительного комплекса WEB-ECOGIS [9; 15] формируется серия динамических многослойных цифровых карт исследуемой территории со слоями рельефа, затоплений, населенных пунктов и дорожной сети. На основе этих данных, а также данных о числе жителей населенных пунктов (вектор ?/ = (^ ₁ ,..., ^)), вместимости ЭТС а и скорости их движения, месте расположения одного или нескольких постоянных эвакуационных пунктов (ЭП) определяются кратчайшие ЭМ и формируется кортеж эвакуационной ситуации E(Q) = ( р, 0 ,t ( Q )) , в котором р = (р 1 ,... ,р _п ) — вектор числа эвакуационных рейсов из каждого НП, значения координат которого пропорциональны числу жителей НП, 0 = ( 0 1 ,..., 0 _П ) — вектор длительностей эвакуационных рейсов, значения координат которого пропорциональны длинам соответствующих ЭМ, т = (т- 1 ,..., т „ ) — вектор периодов безопасной эвакуации жителей НП.

Математическая модель поиска эффективного эвакуационного расписания имеет вид

F(E(Q),Sh(M )) ч extr ,                           (1)

Sh(M )

где F — целевая функция; Sh — расписание движения ЭТС, математическая модель которого определяется при конкретизации задачи (1); M — число ЭТС. В наиболее развернутом виде под расписанием эвакуации мы понимаем матрицу, Sh(M) = dmtjд, j = 1, ..., п; Т = maxт, M = maxMt, Mt = ^>27=i mtj, t = 1, ..., Т, где n — число j                   t эвакуируемых НП; mtj — число ЭТС, одновременно эвакуирующих население из НП j на временном шаге t. Большинство задач типа (1), в том числе задачи оптимизации эвакуационных расписаний, являются NP-трудными, поэтому в настоящей работе строятся эвристические алгоритмы их решения. Число ЭТС (параметр M задачи (1)) определяет конкретизацию задачи (1) и алгоритмы ее решения.

Прежде всего исследуем задачу поиска эффективных безопасных (эвакуирующих все население) эвакуационных расписаний и соответствующий им диапазон значений параметра М . Безопасным расписанием Sh^sec является любое расписание, удовлетворяющее условию

M _j >  1 +

P j

\    , ^{M j —} ^ ^т P j ^j , ^{P j — т j}

^{L a J}          Pj =1

— ⁰ j + ^{1 ,m} t ⁰⁾

— ^m tj ^(t — ¹ , . . . , ^T j ),

^m^ ) ^{— т}^ 1) ^{- m} P j j ,^{(t —} P j , ...,P j ^{+ Q} i ^),m P j j ^{— min} (4S 1) ,..., ^m P i ^—l j ), ^m^^j ) ^{— m}t^{pj - 1}\ ^{(t —} P j + ⁰ j + 1,..., ^T j ^P j ^— 1,.. .^,p j ; J ^{— 1,}...,n.

Задача минимизации числа ЭТС на множестве расписаний (2) имеет вид:

M (E (Q))—max(M _t ) ^ min, M _t — ^тц , t — 1, ..., T. (3) * ^Shec j=i

Эта задача является вариантом задачи ресурсных инвестиций или зеркальной копии расширения классической RCPSP (Resource-constrained project scheduling with time windows) задачи теории расписаний c крайними сроками выполнения работ (deadline) [13].

Представим три эвристических алгоритма решения задачи (2), (3). Первый алгоритм A i представляет собой многошаговый процесс перераспределения ЭТС между ЭМ после окончания эвакуации на очередном ЭМ. При каждом перераспределении составляется новое безопасное расписание эвакуации. Начальным безопасным расписанием эвакуации считается расписание движения ЭТС, реализующее эвакуацию всего населения НП по каждому маршруту i за время, не превышающее предельно допустимого значения т ^ , в котором каждое ЭТС перемещается по единственному ЭМ. Это расписание составляется элементарным расчетом. В момент появления резерва на одном или нескольких ЭМ (высвобождения одного или нескольких ЭТС) на шаге к (в момент времени t h (к — 1, 2,..., К ) ) он может быть назначен на один из ЭМ или распределен по частям на несколько ЭМ. Для каждого потенциально возможного назначения резерва составляется улучшенное безопасное расписание движения по соответствующему ЭМ с максимальным уменьшением числа ЭТС на этом маршруте в начальном расписании. Если максимум этого уменьшения достигается на единственном ЭМ, то соответствующее назначение принимается. Если максимум достигается на нескольких ЭМ (в количестве J _k ), то для каждого из них рассчитывается улучшенное допустимое расписание эвакуации и вычисляется момент появления его резерва t _kj и его величина m _kj (j — 1, 2,...,J _k ) . Назначение производится на ЭМ с максимальным значением индекса резерва IR _kj — ^r- ^ ^jjL . Если максимум этого индекса достигается на нескольких ЭМ, то назначение резерва происходит на ЭМ, отвечающий минимальному значению t hj . При равенстве этих величин для нескольких ЭМ назначение производится на любой из них. Распределение резерва ЭТС на несколько ЭМ производится в случае его избыточности для одного ЭМ по описанному выше правилу. Излишек ЭТС распределяется аналогично. Алгоритм завершается после высвобождения всех ЭТС. Этот алгоритм и результаты его численной реализации для ВАП приведены ранее в [16].

Второй алгоритм А ₂ формирует расписание поэтапно, расширяя список эвакуируемых НП, в порядке роста их индекса потенциальной эффективности использования

ЭТС (ИПЭ) ^ i = | i , (^ = 1,...,n) . При малом числе НП минимально необходимое число ЭТС определяется полным перебором вариантов. При добавлении очередного НП алгоритм исследует возможность безопасной эвакуации его жителей за счет освободившихся единиц ЭТС без изменения уже составленной части эвакуационного расписания. При невозможности составления такого расписания к числу используемых ЭТС последовательно добавляется по одному ЭТС до тех пор, пока не будет достигнут успех.

Третий алгоритм A 3 представляет собой попытку построения безопасного расписания при фиксированном числе ЭТС. Расписание строится последовательным распределением ЭТС между НП в каждый момент дискретного времени, от конца общего периода эвакуации к его началу. При распределении более высокий приоритет имеют маршруты с наибольшим ИПЭ. Таким образом, на каждом шаге по времени алгоритм максимизирует резерв ЭТС, который может использоваться на маршрутах с минимальными ИПЭ. Алгоритм останавливается либо при построении расписания, либо при невозможности выполнения условий безопасного расписания в некоторый момент времени. В случае успеха число ЭТС уменьшается на 1, в случае неудачи — увеличивается на 1. Обозначим М^ число ЭТС в начальном расписании алгоритма A 1 решения задачи (2), (3), а минимальное из ее решений, найденных алгоритмами A 1 ,A 2 ,A 3 — М^ .

Наиболее эффективное решение задачи (2), (3) достигается использованием всех трех алгоритмов. Алгоритм A 3 может использоваться для улучшения решения, найденного алгоритмами A±,A 2 . Алгоритм A 2 позволяет получить нижнюю оценку решения задачи (2), (3) — М 1 (к) , равную числу ЭТС, найденному полным перебором вариан- ^

тов на его первых к этапах. Эта оценка учитывает «узкие места» задачи, поэтому может быть очень близка к решению задачи и даже совпадать с ним. Но поскольку значение к , как правило, не превышает нескольких единиц, эта оценка заведомо эффективна лишь при небольшом числе НП. Другая нижняя оценка решения М 2 , не зависящая от числа ^

НП и определяющаяся системой неравенств

т

(М 2 - 1)т< ^ M t < М 2 Т, Z—~S                                                       Z—'.

t=1

при малом числе НП обладает меньшей точностью, чем М 1 . ^

В таблице 1 представлено два расписания, соответствующие одному и тому же решению задачи (2), (3), найденному алгоритмами A 1 — A 3 , для модельного примера: Е = ^р, 0 , т ^ : р = (5, 2,10,20,12, 8), 0 = (2,4,4, 2, 3, 3), т = (13,4, 20, 8,10,15) . В ней столбцы отвечают дискретным моментам времени, строки — НП, в ячейках указаны числа ЭТС. Числа ЭТС, соответствующие расписанию, найденному алгоритмами A 1 и A 2 , указаны сверху, а числа ЭТС, соответствующие расписанию, найденному алгоритмом A 3 — снизу. Для этого примера начальное распределение ЭТС в алгоритме A 1 описывается вектором тп ₀ = (1, 2, 2, 5,4, 2) , вектор ИПЭ имеет вид с? = (6, 5;2;5;4;3,3;5),М 1 (1) = ^

= 2; М 1 (2) = 5; М 1 (3) = 10; Т = 20; М 2 = 8 ; M ₀ ^sec = 16 , М[^ес = М 1 (3) = 10 ^      ^             ^

т ^M_t = 158. t=i

В оптимальном расписании, найденном алгоритмом A 1 , начальное распределение ЭТС описывается вектором m 0 ^pt = (0, 2, 0, 5, 3, 0) . Как показывает таблица 1, алгоритм A 3

«сдвигает» расписание эвакуации жителей НП с большими эвакуационными периодами к их концам, за счет этого данный алгоритм обладает наибольшей потенциальной эффективностью, но также и наименьшей устойчивостью к ошибкам при оценке параметров эвакуационной ситуации.

Таблица 1

Два расписания, соответствующие решению задачи (2) и (3) для модельного примера

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	0	0	0	0	0	0	0	0	2	2	3	3	0	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	5	5	0	0	0	0	0	0	0	0
2	2	2	2	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	2	2	2	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0	0	0	0	3	9	10	10	7	1	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	10	10	10	10
4	5	5	5	5	5	5	5	5	0	0	0	0	0	0	0	0	0	0	0	0
	4	4	8	8	8	8	0	0	0	0	0	0	0	0	0	0	0	0	0	0
5	3	3	3	3	5	5	5	4	4	1	0	0	0	0	0	0	0	0	0	0
	0	0	0	0	2	2	2	10	10	10	0	0	0	0	0	0	0	0	0	0
6	0	0	0	0	0	0	0	1	4	7	7	4	1	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	0	10	10	10	0	0	0	0	0

Для обеспечения возможности безопасной эвакуации населения при меньшем числе ЭТС на каждом ЭМ должен быть создан временный ЭП. При использовании временных ЭП эвакуация населения проводится в два этапа: первый — эвакуация всех жителей из НП во временные ЭП, второй — их эвакуация из временных ЭП в постоянные. Для определенности местом расположения временного ЭП на каждом ЭМ можно считать ближайшую к НП точку (ячейку цифровой карты территории), путь от которой до постоянного ЭП не затапливается согласно прогнозу развития наводнения.

Безопасное расписание эвакуации во 2-м акте должно удовлетворять условию (4)

(2) ^{P j}

^(2) = E m Pj j, mtj = m pj=i

(0) ' tj

(p j )         (p j - 1)

^m tj ^j = ^m tj ^j    - ^m P j j ,

(P j - 1) m _{P j} j = min(m' _pj

., m

⁽ P j ^{- 1)} P j + ⁰ j ^j

),

' Щ + 1 <  lifp, ^j

a

до временных ЭП и расстояниями от временных ЭП до постоянных. С учетом этих изменений задачи поиска минимального числа ЭТС на множестве безопасных расписаний 1-го и 2-го акта эквивалентны задаче (2), (3). Обозначим их решения соответственно М 21 и М:^ . Минимальное число ЭТС, обеспечивающих безопасную двухактную эвакуацию, равно М 2'"' = та^М^, М^) .

Если имеющееся число ЭТС М удовлетворяет неравенствам M 2e < М < М 1^ес, то для снижения затрат на организацию временных ЭП необходимо решить задачу оптимального разделения ЭТС на группы, участвующие соответственно в 2-актной и 1-актной эвакуациях. Оптимизация разделения достигается формированием группы 1актной эвакуации из НП с наибольшими значениями индекса ИПЭ в количестве, обеспечивающем безопасную эвакуацию их жителей при числе ЭТС, равном М — М2^ес .

Если М 21 <  М < М:^ , то для снижения агрегированного жизненного риска эвакуирующегося во 2-м акте населения, возникающего при превышении предельного времени их пребывания во временных ЭП, необходимо решить следующую задачу

LR(E(Q),Sh(M )) —^ min ) ,

П N ;

lr = ЕЕ и„М£ i=1 j=1

< М < М^.

Здесь величина отрезка времени, проведенного j -м жителем г -го НП на временном ЭП. Эвристический алгоритм решения задачи (4), (5) заключается в формировании двух и, возможно, нескольких очередей эвакуации для каждого числа имеющихся в наличии ЭТС. Для формирования первой очереди составляется первый рейтинговый список НП в порядке роста их ИПЭ. Первая часть алгоритма заключается в последовательном решении задачи (3), (4) для групп НП, полученных после исключения из их совокупности по одному НП в порядке их следования в рейтинговом списке. Результатом реализации первой части алгоритма является последовательность решений серии задач (3), (4) для групп НП с уменьшающимся общим числом М ^(к) , к = 1,..., К (К <  п) . Если для одного или нескольких значений к интервалы (М ^(к) ,М ^(к+1) ) оказываются достаточно большими, то во второй части алгоритма для их разбиения на части после соответствующего шага к в группу исключаемых из эвакуации НП следует добавлять один или несколько НП с более высокими значениями ИПЭ. Для НП, исключенных из первой очереди, формируется вторая очередь эвакуации при помощи изложенного выше алгоритма. В случае исключения из нее некоторых НП формируется третья очередь и т. д.

Если имеющееся число ЭТС М удовлетворяет неравенству М < М2^ , то нужно проанализировать возможность проведения полной безопасной двухактной транспортносухопутной эвакуации, при которой население НП, удаленных от своих временных ЭП на расстояние пешеходной доступности, проходит путь до своих временных ЭП пешком. Эта задача исследована нами в [17] и поэтому здесь не рассматривается.

Обозначим М3^ес минимальное число ЭТС, обеспечивающее 1-й акт полной безопасной транспортно-пешеходной эвакуации населения. В случае М < М3^ес при наличии временных ЭП или в случае М < М1^ес при их отсутствии необходимо решить две задачи поиска оптимального расписания частичной сухопутной эвакуации. Первая из них — задача максимизации числа эвакуированных жителей территории имеет следующий вид

^ эв (E (Q'),Sh(M ))     >  max .

Sh(M )

В случае одновременного окончания эвакуации, когда все НП затапливаются практически одновременно, решение задачи (6) отвечает расписанию, в котором эвакуация ведется последовательно из НП, упорядоченных в порядке роста длительности периодов их эвакуации (при двухактной эвакуации — длительностей периодов 1-го акта эвакуации). В случае существенно различных эвакуационных периодов задача (6) решается алгоритмом решения задачи (5) с формированием только одной эвакуационной очереди. В таблице 2 приведены результаты реализации данного алгоритма для рассмотренного выше модельного примера.

Результатом работы 1-й части алгоритма является последовательность, содержащая 5 значений ЭТС (9, 7, 5, 3, 2). Еще 4 значения (8, 6, 4, 1) были добавлены в эту последовательность в результате реализации второй части алгоритма.

Таблица 2

Пример результата решения задачи (6) для модельного примера

Число ЭТС	Число рейсов	Эвакуируемые НП	Исключенные НП
1	5	1	2-5
2	10	3	1;2;4;5;6
3	15	1;3	2;4;5;6
4	18	3;6	1;2;4;5
5	23	1;3;6	2;4;5
6	38	3;4;6	1;2;5
7	43	1;3;4;6	2;5
8	45	1;2;3;4;6	5
9	55	1;3;4;5;6	2
10	57	1-6	—

Математическая формулировка второй задачи оптимизации расписания частичной сухопутной эвакуации имеет вид:

LR ^H (E(QVSh(M )) — > min .                       (7)

Sh(M )

Здесь nH

LRH = ^ LRH - i=i агрегированный гидрологический риск жителей nH НП, не эвакуированных сухопутным транспортом, где ti — время, проведенное жителями НПi на затопленной территории. Эта задача решается тем же алгоритмом, что и задача (6).

2.    Результаты реализации алгоритмов для ВАП

Результаты вычислительных экспериментов по моделированию динамики затопления территории ВАП для Q Е [25000; 60000] мг показали, что затопление НП начинается при Q >  29000 м ^ и растет в течение первых 4-х суток. На рисунке 2 приведены зависимости от времени числа жителей затапливаемых населенных пунктов ВАП для различных значений гидрографа ВГЭС.

Перечень участков дорог, составляющих ЭМ для каждого из 56 НП ВАП, приведен в таблице 3. В таблице 4 указаны число жителей НП, длины ЭМ и длительности пе- риодов одноактной эвакуации, длины маршрутов 1-актной (L, км), 2-актной (L1,L2, км) сухопутной и водной (Lh) эвакуации.

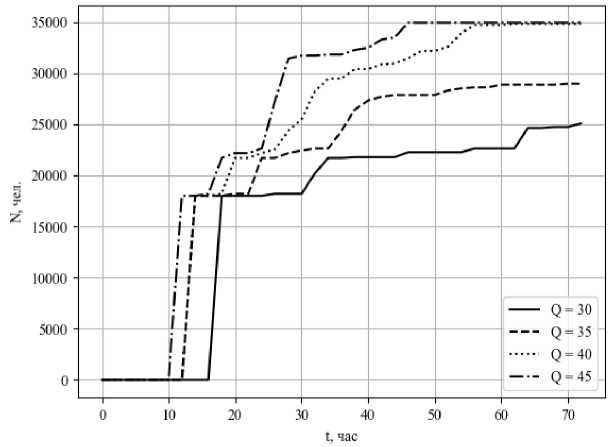
Рис. 2. Зависимости от времени числа жителей затапливаемых населенных пунктов ВАП для Q = 30; 35; 40; 45 тыс. м ³ /с

Число ЭТС (вместимость — 40 чел.), обеспечивающих безопасную эвакуацию населения ВАП при использовании расписания, минимизирующего общее время эвакуации (что достигается одновременным завершением всех эвакуационных рейсов) в отсутствие прогноза развития наводнения для эвакуации всего населения ВАП за 1 рейс, равно 875, а при установлении в качестве общего для всех НП эвакуационного периода безопасной эвакуации минимального из них, равного в рассматриваемом диапазоне чрезвычайных гидрографов 13 часам (см. табл. 4), необходимое число ЭТС снижается до 115. При использовании расписания, максимизирующего число эвакуируемых жителей ВАП за любой период времени (последовательная эвакуация из НП, упорядоченных в направлении роста эвакуационных периодов), безопасная эвакуация населения ВАП требует от 65 до 85 ЭТС.

Найденные в результате численной реализации описанных выше моделей и алгоритмов числа ЭТС, реализующие безопасную эвакуацию населения ВАП при нескольких значениях расхода ВГЭС Q и моментах времени начала эвакуации t ₀ , отсчитываемых с момента начала моделируемых наводнений, приведены в таблицах 5—7.

В таблице 5 приведены значения M ₀ ^sec ,M ₁ ^sec (A ₁ ),M ₁ ^sec (A 3 ) для расписаний одноактной эвакуации, рассчитанных соответственно алгоритмами A 1 и A 3 . В таблице 6 приведены рассчитанные алгоритмом A 3 значения М ₂“ , обеспечивающие 1-е акты расписаний двухактной эвакуации в задаче (3), (4) без учета 2-го акта. В таблице 7 приведены рассчитанные алгоритмом A 3 решения задачи (3), (4) при величинах M 2^ ,M 2%c , обеспечивающих безопасную двухактную эвакуацию всех жителей ВАП одним и тем же составом ЭТС. Обеспечение выполнения ограничения времени пребывания эвакуируемого населения во временных ЭП величиной Т max = 24[ ч ] потребовало сокращения периодов эвакуации в 1-м акте, что повлекло за собой увеличение минимального числа ЭТС.

Таблица 3

Номер эвакуационного маршрута	Список дорог эвакуационного маршрута	Номер эвакуационного маршрута	Список дорог эвакуационного маршрута
1	66,75,26	25	38,8,9,10
2	75,26	26	19,8,9,10
3	26	27	65,75,26
4	10	28	67,78,65,75,26
5	55,74,77,54,68,1,0	29	63,20,9,10
6	59,17,76,16,4,3,2,1,0	30	18,7,8,9,10
7	17,76,16,4,3,2,1,0	31	74,77,54,68,1,0
8	58,57,14,0	32	77,54,68,1,0
9	76,16,4,3,2,1,0	33	61,55,74,77,54,68,1,0
10	80,2,1,0	34	70,60,17,76,16,4,3,2,1,0
11	32,5,4,3,2,1,0	35	60,17,76,16,4,3,2,1,0
12	51,49,47,46,36,7,8,9,10	36	62,70,60,17,76,16,4,3,2,1,0
13	50,69,48,46,36,7,8,9,10	37	72,62,70,60,17,76,16,4,3,2,1,0
14	49,47,46,36,7,8,9,10	38	68,1,0
15	14,0	39	53,14,0
16	44,73,43,0	40	23,10
17	45,27,0	41	2,1,0
18	69,48,46,36,7,8,9,10	42	52,69,48,46,36,7,8,9,10
19	27,0	43	43,0
20	46,36,7,8,9,10	44	78,65,75,26
21	42,10	45	29,3,2,1,0
22	41,9,10	46	25
23	22,10	47	35,6,5,4,3,2,1,0
24	40,9,10	48	33,5,4,3,2,1,0

Таблица 4

Длительности эвакуационных периодов и длины маршрутов 1-актной ( L, км ) , 2-актной ( L 1 ,L 2 , ) сухопутной и водной ( L_h) эвакуации («—» — отсутствие затопления)

НП	Число жителей	Длительность эвакуационного периода (часы)				L	L 1	L 2	L h
		Q = 30	Q =35	Q = 40	Q =45
1	1330	—	70	56	48	16	10	6	11
2	100	—	—	—	50	7	5	2	6
3	2000	—	—	—	—	6	3	3	3
4	1500	68	42	34	30	2	2	0	5
5	200	31	27	24	23	22	9	13	9
6	165	—	58	44	37	34	11	23	8
7	1650	—	58	46	39	30	11	19	9
8	800	46	36	31	28	21	10	11	9
9	100	—	—	—	47	18	2	16	11
10	800	—	—	—	53	12	0	12	7
11	430	67	46	37	32	20	3	17	10
12	800	39	30	27	25	22	9	13	9
13	950	38	31	27	24	26	8	18	12
14	720	48	37	32	28	19	8	11	11
15	18 000	40	32	28	25	10	2	8	3

НП	Число жителей	Длительность эвакуационного периода (часы)				L	L 1	L 2	L h
		Q = 30	Q =35	Q = 40	Q =45
16	200	21	19	18	17	14	2	12	5
17	170	18	16	14	13	15	6	9	9
18	480	39	31	27	25	23	7	16	12
19	300	41	31	27	24	12	5	7	9
20	180	67	47	38	32	14	6	8	11
21	80	62	46	38	33	7	4	3	9
22	100	62	46	38	33	8	4	4	9
23	100	39	30	27	25	21	7	14	8
24	300	—	—	46	35	7	2	5	7
25	345	—	—	—	—	3	1	2	7
26	80	—	50	40	34	9	4	5	9
27	100	—	56	43	36	8	4	4	9
28	350	—	53	42	36	11	6	5	11
29	250	—	59	49	43	15	8	7	9
30	205	—	59	49	43	21	13	8	14
31	100	—	59	46	40	14	8	6	17
32	100	—	51	41	35	12	8	4	16
33	270	—	51	40	35	16	6	10	9
34	170	—	—	69	50	15	3	12	12
35	100	—	—	69	50	15	3	12	13
36	120	31	27	24	23	27	12	15	7
37	230	—	50	41	36	35	13	22	8
38	340	—	50	41	36	33	13	20	9
39	120	39	33	30	28	41	17	24	9
40	350	39	33	30	28	48	19	29	15
41	185	—	—	—	—	10	0	10	8
42	300	—	61	46	38	14	3	11	6
43	80	62	43	35	30	5	1	4	6
44	100	—	—	—	—	10	0	10	6
45	100	—	—	—	—	9	0	9	6
46	80	39	31	27	25	24	10	14	10
47	100	—	69	49	40	10	2	8	5
48	2000	55	38	31	27	8	1	7	5
49	100	—	—	—	50	7	7	0	8
50	185	—	—	—	50	7	7	0	8
51	100	—	59	49	43	16	9	7	10
52	100	—	59	49	43	17	10	7	11
53	200	—	—	—	—	14	0	14	7
54	460	58	47	39	35	10	5	5	3
55	10	—	57	41	34	20	4	16	12
56	20	67	47	38	33	19	2	17	10

Таблица 5

Решения задачи (2), (3) M ₀ ^sec /M ₁ ^sec ( 4 ₁ ) /.M ₁ ^sec ( A ₃ ) для серии значений расходов ВГЭС Q [ м- ] и моментов начала эвакуации t ₀ [ часа ]

	Q = 30	Q =35	Q = 40	Q =45
0	35/26/19	57/42/20	63/47/26	70/56/27
2	35/27/20	57/43/22	64/49/27	73/58/30
4	36/28/21	59/44/24	66/51/29	76/59/32
6	38/28/21	61/46/26	69/52/32	79/63/35
8	39/29/22	63/48/28	73/56/33	82/66/38

Таблица 6

Решения задачи (3), (4) М2Ч^С без учета 2-го акта для серии значений расходов ВГЭС Q [ мт ] и моментов начала эвакуации t ₀ [ часа ]

	Q = 30	Q =35	Q = 40	Q =45
t o = 0	14	17	20	23
t o = 2	15	18	21	25
t o = 4	16	20	23	27
t o = 6	16	21	25	30
t o = 8	17	23	27	32

Таблица 7

Решения задачи (3), (4) М^/М^ при Т max = 24[ часа ] для серии значений расходов ВГЭС Q [ мсг ] и моментов начала эвакуации t ₀ [ часа ]

	Q = 30	Q =35	Q = 40	Q =45
t o = 0	19/11	25/16	26/18	28/19
t o = 2	20/11	26/16	29/18	31/19
t o = 4	20/11	28/16	30/18	31/19
t o = 6	21/11	30/16	32/18	33/19
t o = 8	23/11	31/16	34/18	36/19

Анализ таблиц 5—7 показывает, что эффективность решения оптимизационной задачи (2), (3) алгоритмом А 1 находится в диапазоне 1,24—1,34, а алгоритмом А 1 — в диапазоне 1,77—2,85. Использование оптимальной 2-актной эвакуации (решений задачи (3), (4)) позволяет дополнительно сократить необходимое число ЭТС в 1,18—1,36 раз либо в случае выполнения 2-го акта эвакуации дополнительными ЭТС, подключившимися к работе через Т max = 24[ ч ] , либо при существенном увеличении значения Т max .

На рисунке 3 приведены решения задач (6) и (7) для ВАП — зависимости величины жизненного риска (LR) и числа эвакуированных жителей (N) от числа ЭТС в оптимальных расписаниях частичной эвакуации.

Анализ рисунка 3 позволяет заключить, что решения задач (6) и (7), определяющие оптимальную группу эвакуируемых НП при каждом значении имеющихся в наличии ЭТС, совпадают и определяются величинами ИПЭ.

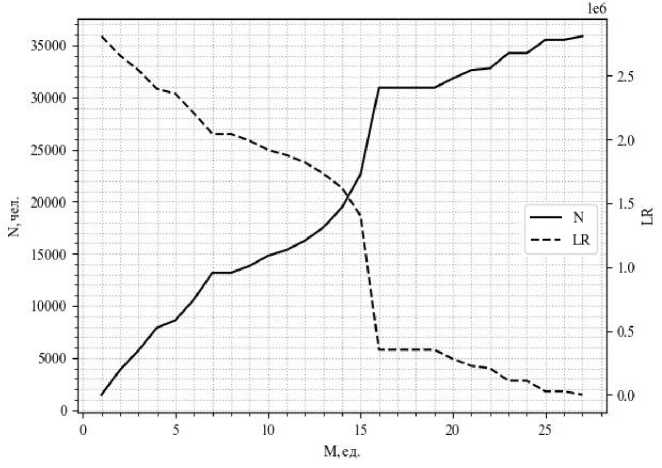
Рис. 3. Решения задач (6) и (7) для ВАП: зависимости величин жизненного риска (LR) и числа эвакуированных жителей (V) от числа ЭТС в оптимальных расписаниях частичной эвакуации

Заключение

В настоящей работе представлена общая задача поиска расписаний организованной транспортной эвакуации населения территорий речных долин и пойм, минимизирующих величину агрегированного жизненного риска, при наличии прогноза речного гидрографа на основе гидродинамического расчета моментов затопления населенных пунктов и участков дорог, а также серия ее частных версий для ряда возможных эвакуационных ситуаций.

Представлено несколько эмпирических алгоритмов поиска минимального числа ЭТС, обеспечивающих безопасную эвакуацию всего населения при известных значениях параметров эвакуационной ситуации. Исследована сравнительная эффективность использования постоянных и временных ЭП в зависимости от количества имеющихся ЭТС и условий пребывания населения во временных ЭП.

Также предложен эмпирический алгоритм построения эффективных расписаний, обеспечивающих частичную эвакуацию населения в условиях дефицита ЭТС.

В результате серии вычислительных экспериментов показано, что реализация предложенных алгоритмов поиска оптимальных расписаний эвакуации населения ВАП, основанных на численных гидродинамических имитациях наводнений, позволяет значительно сократить число ЭТС, обеспечивающих безопасную эвакуацию всего населения. Найдены границы числа ЭТС, обеспечивающих безопасную эвакуацию населения ВАП в зависимости от значений чрезвычайного гидрографа Волжской ГЭС и моментов начала эвакуации. Построены эффективные расписания, обеспечивающие частичную эвакуацию населения ВАП в условиях дефицита ЭТС.

Перспективным направлением развития результатов настоящей работы являются алгоритмы построения эффективных эвакуационных расписаний в условиях неопределенности параметров эвакуационной ситуации и адаптивных алгоритмов их формирования в условиях внезапного изменения этих параметров в процессе эвакуации.