Модели определения запаса инфекции в почве
Автор: Цугленок Н.В., Никулочкина С.Н.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Почвоведение и растениеводство
Статья в выпуске: 7, 2012 года.
Бесплатный доступ
В статье предложен теоретический подход построения схемы морфологического моделирования запаса инфекции в почве и разработаны динамические модели влияния осадков на уровень запаса инфекции в почве, в зависимости от распределения по временной и природно-экологической структурам. Установлено, что результаты исследований с учетом атмосферной циркуляции, теплового и водного балансов растений, а также применения удобрений необходимы при планировании эффективного производства сельскохозяйственных культур в Красноярском крае.
Запас инфекции, атмосферные осадки, влага, почва, динамическая модель, морфологическое моделирование, временная структура, природно-экологическая структура
Короткий адрес: https://sciup.org/14082536
IDR: 14082536 | УДК: 639.2.053.8
Текст научной статьи Модели определения запаса инфекции в почве
Введение. Земледелие в отличие от других производств характеризуется своеобразием производственного процесса и вместе с тем огромной зависимостью конечного результата от множественного количества факторов жизни. Обязательными условиями жизнедеятельности растений являются свет, тепло, вода, воздух и питательные элементы. Эти факторы жизни растения получают из космоса, атмосферы и почвы. Космические факторы жизни растений практически не регулируются в земледелии и в значительной мере определяют уровень энергопродуктивности растений.
Актуальность исследований. Применение разработанных динамических моделей для учета запаса инфекции в почве, являющейся одним из важнейших лимитирующих факторов, необходимо применять для планировании сельскохозяйственных культур. Мероприятия, включающие в себя защитные меры, снижают инфекционный порог, амплитуду колебаний продуктивности, повышая качество готовой продукции растениеводства
Цель исследований. Разработать схему морфологического моделирования и динамических моделей влияния осадков на уровень запаса инфекции в почве в зависимости от распределения по временной и природно-экологической структурам.
В задачи исследований входило: выявить закономерности двойственного действия биофизических факторов в системе агрофитоценозов в зависимости от запаса инфекции в почве, влияющие на формирование продуктивности культур.
Объекты и методы исследований. Объектами исследований являются сельскохозяйственные культуры, возделываемые при влиянии осадков [1], атмосферной циркуляции, теплового и водного балансов растений на уровень запаса инфекции в почве, в зависимости от распределения по временной и природноэкологической структурам. Использован аппарат теории рядов Фурье, пакет Maple.
Результаты исследований и их обсуждение. В условиях Красноярского края определяющим фактором является наличие влаги в почве. Исследованиями установлено, что на урожайность культур наиболее существенное влияние оказывают запасы влаги в почве в период посева, кущения. Поэтому для составления модели были взяты запасы влаги в почве в указанные периоды. Экспериментальные данные многочисленных исследований свидетельствуют, что объективным показателем обеспеченности почвы доступными элементами питания является содержание нитратного азота в почве весной перед посевом.
Разработка теоретических основ моделирования методов, изложенных [2], и технологических приемов сохранения и повышения плодородия почв [1,3] является очень сложным процессом.
Разработка схемы морфологического моделирования запасов инфекции в почве обусловлена многообразием агроэкологических факторов, влияющих на фиксацию солнечной энергии и превращение ее в энергию органического вещества. Начинать этот процесс рекомендуется с разработки функциональной схемы исследований. Предварительное изучение взаимосвязи урожайности сельскохозяйственных культур, размещаемых по чистому пару, позволило выделить основные факторы: суммарную солнечную радиацию ( x 1 ), сумму температур ( x 2 ), количество атмосферных осадков за вегетационный период ( x 3 ), запасы доступной влаги в метровом слое почвы в период посева ( x 4 ) и кущения ( x 5 ), содержание нитратного азота весной перед посевом ( x 6 ).
В связи со сказанным, модель запаса инфекции в почве предлагается отыскивать в виде следующей регрессионной функции:
u(x 1; x2; x3; x4; x5; x6) = a 1 x 1 + a2 x2 + a3 x3 + a4 x1 + a5 x2 + a6 x3 + a7 x 1 x2 + a8 x2 x3 + aaa 2 22
+ a 9 x1 x 3 + a 10 x 1 x 2 x 3 +---1---1---+ a 14 x 4 + a 15 x 5 + a 16 x 6 + a 17 x 4 + a 18 x 5 + a 19 x 6
x1 x2
+ a 20 x4 x5 + a 21 x5 x6 + a 22 x4 x6 + a 23 x4 x5 x6 +—— +—— +—— + a 27, x4 x5
где u – уровень инфекции %; x 1 – солнечная радиация за вегетационный период, ккал/см2 с; x 2 – осадки, мм; x 3 – температура, 0С; x 4 – запасы доступной влаги в метровом слое в период посева, мм; x 5 – запасы доступной влаги в метровом слое в период кущения, мм; x 6 – содержание нитратного азота в слое 0…40 см, мг/кг. Морфологическое моделирование влияния основных экологических факторов на запас инфекции в почве (рис. 1) базируется на прямом и обратном действии каждого из управляющих факторов.
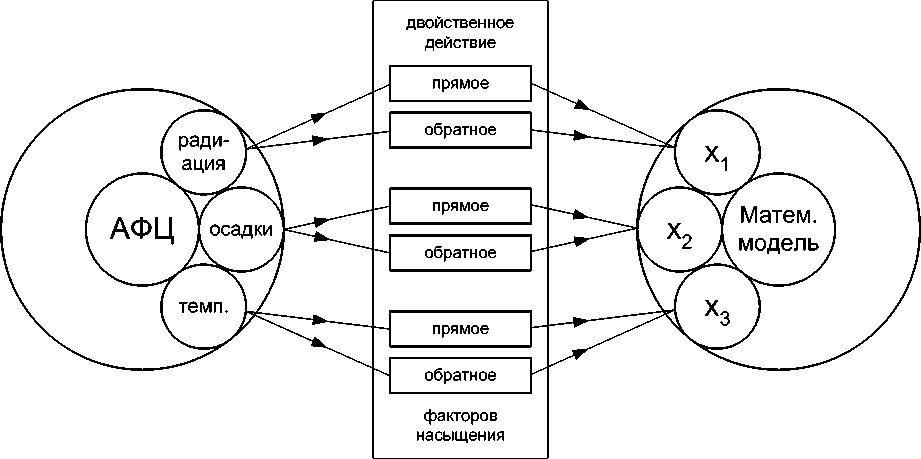
Рис. 1. Схема морфологического моделирования запаса инфекции в почве
Прямое действие связано с насыщением агроэкологическими ресурсами природной среды до некоторой предельной точки, приводящими к росту биомассы. Перенасыщение ресурсами соответствует обратному действию факторов. В результате расчетов на языке Maple по экспериментальным данным найдены следующие зависимости уровня инфекции.
Эффективность использования солнечной энергии растениями изменяется во времени. При наличии других факторов жизни с ростом освещенности интенсивность фотосинтеза вначале повышается пропорционально облученности. Но так происходит до определенного предела, который характеризуется так называемым световым насыщением.
При суммарной положительной температуре в промежутке от 1000 до 2000 0С, происходит рост биомассы растения. При запасах влаги в почве в период посева от 50 до 200 мм наблюдается прирост биомассы, а свыше 200 мм этот процесс замедляется.
В исследованиях продуктивности сельскохозяйственный культур в структуре звеньев полевых севооборотов наряду с экспериментальным подходом возникает необходимость разработки теоретических моделей для прогнозирования и системного описания энергетических потоков в системе агрофитоценоза.
Результаты предварительного поиска вида регрессии показали, что в качестве регрессионной функции нельзя брать многочлены, тригонометрические полиномы, комбинации логарифмических и показательных, дробно-рациональных функций, поскольку при таком выборе теоретической поверхности отклика погрешности превышают допустимые пределы в агрономии. Не удается выразить регрессию через комбинацию элементарных функций. Результаты расчетов показывают, что средние показатели урожайности, энергетической и экономической (при фиксированной цене) продуктивности сельскохозяйственных культур в структуре звеньев севооборотов имеют меньшую амплитуду колебаний по сравнению с аналогичными функциями состояний отдельных звеньев.
Они имеют более устойчивую квазипериодическую динамику, менее зависящую от биоциклов инфекции в почве и более пригодную для решения задачи планирования отрасли растениеводства.
Динамическая модель запаса инфекции в почве в зависимости от распределения осадков по природно-экологической структуре. Многолетние наблюдения за изменениями осадков и запаса инфекции в почве вместе со статистическим анализом этих данных показывают нерегулярный характер циклических колебаний этих процессов, распределенность их по территории и как следствие непредставимость в линейном или полиномиальном виде.
Следовательно, разрабатываемая модель должна учитывать дифференцируемость агроэкологических зон, цикличность процесса по географическим координатам и времени.
Для решения подобных задач наиболее приспособленным является аппарат рядов Фурье, отрезок которого является тригонометрическим многочленом ф , приближающим неизвестную функцию f в замкнутой области Z с любой наперед заданной точностью s :
II f - 4 Е< S .
Пусть x – восточная долгота; y – северная широта; Tt , и Tx , Ty – временные и, соответственно, пространственные факторные периоды, мес.; U (t, x, y) - запас инфекции на 1 мм осадков в момент времени t в точке с географическими координатами U(t, x, y), соответствующими центру агроэкологической зоны.
Тогда в силу периодичности процесса по географическим координатам коэффициенты G ( x , y ) функции U в точке с географическими координатами ( x , y ) имеют вид
( n
G = C + z A
7 n y
k k x = 1 7
k
x , kx
cos
_ А
2 kx ^ x
+ XA.
^ n y
k ky < y nx
k
zz
k k y = 1
k k x = 1
y , k y
cos
k T x
( 2 k y n y 1
k
T y
+ Bx k sin x , kx
+ B y , k y
a kx , ky cos
2 kx n x
А
T k T 7
cos
( 2k. n t k T
. 2 k n y Sin —t——
k
2 n y
T
T y
k
+
+
+
k y 7
Г n y
Г П х
+ X X b
Г n y
к кУ = 1
Г П х
к к х = 1
’кх , ку sin
Г 2 кх п х Л
к Т х
cos
2 кУ П У
к
T
к
к
+
XX
к кУ = 1
к к х = 1
c kx , ky
cos
Г2кх пхЛ к T 7
■ Г 2 ку П У sin —----
y
Л
к
+
Г n y
Г П х
+ XX d
к кУ = 1
к к х = 1
кх , ку sin
Г2кх пхЛ к 1 х 7
к у 7
. Г 2 ку ^У sin —----
Т к у
А Л Л
7 7 7
,
где A, B , a , b , c , d - коэффициенты разложения процесса G ( t , x , y ) в тройной ряд Фурье по переменным t , x , y . Регрессионную функцию поля осадков также представим в виде ряда Фурье с указанными выше коэффициентами:
r
n 1
U = c ( х , У )+ X ' к к = 1 к
a l, к ( х , У ) cos
Л 2 п к t y
Г n
+ X к к =1 к
a
'2, к ( x, y ) cos l
к
2 п к t
T 1 7
+ ь 1, к ( x , У ) sin
г 2 п к t
<
+
n 3
+ X кк=1 к
a
'3, к ( x , У ) cos
Г n
+ X к к=1 к
a
'4, к ( х , У ) co s
Г n 5
+ X кк=1 к
a 5, k
( x , y ) cos
Т
T 2
2. п kt
+ b 2, к ( х , У ) sin
г 2 п кt Л
к
к
т
T 3
2 п к t
к T 4
г 2 п к t
+ b з, к ( х , у ) sin
к т 5 7
+ b 4, к ( x , y ) sin
+ Ь 5, к ( x , У ) sin
к
T 2 77 2 п к t Л
T 3 77 2 п к t Л
к T 4
г 2пк t к T
+
,
+
+
где a , b – коэффициенты разложения в ряд Фурье.
В результате подстановки данных в модель распределения инфекции в почве на 1 мм осадков на территории края будет выражаться через три независимых переменных – времени и двух географических координат (рис. 2).
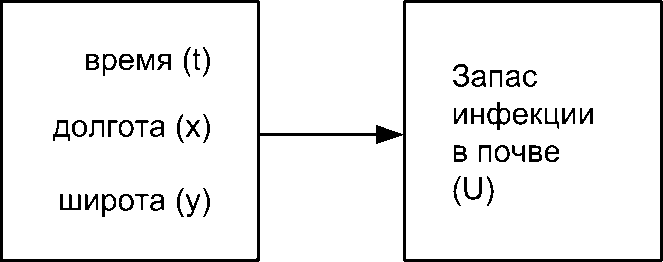
Рис. 2. Распределение запаса инфекции в почве
Динамика запасов инфекции зависит от динамики осадков и изменения температурного режима и поэтому может быть описана моделью с регрессионной функцией вида.
Динамическая модель запаса инфекции в почве в зависимости от распределения осадков по временной структуре. В качестве математического аппарата для моделирования динамики запаса инфекции в почве в зависимости от динамики осадков целесообразно использовать гармонический анализ Фурье от трех переменных, который может учесть нерегулярный характер колебаний двух связываемых процессов.
Пусть u – уровень инфекции в почве за год, %; v – за вегетационный период, %; x – восточная долгота; y – северная широта; Tt , и Tx , Ty – временные и, соответственно, пространственные факторные периоды, мес. Обозначим через Q - поле средней инфицированности в момент времени t в агроэкологической зоне с центром в точке с координатами (x, у). Исходя из априорной цикличности процесса выпаде- ния осадков по времени, периодичности по географическим
координатам представим функцию
Q ( t , u , v , x , у ) в виде
Г
° C + Е A t , kt cos
2 k t n t
7 n
v
k k t = 1 ( v (
k
t
т k t
+ Bt , k, sin
( 2 kt nt 1 1
k T t 77 7
+
+ Е A x , k t cos
2 k t n u
( П
k k u = 1 k 7
t
T k U
+ B
x , kt
Sin
2 kt nu ~k~ k T u
\
+
Е A y , k t cos
7А/ _ k 2 k v n v
k k v = 1 k
( n
+ ХЕЕ
k k v = 1
( nv
k k u = 1
7 JL.
k k t = 1
(
t
k
Г v 7
+ B
y , kt
Sin
( 2 k v n v 11
7 k
a kt , ku , kv cos
2 k t n t
k
T t
cos
k
( 2k
Tv k nu
+
+ Е Е ЕЛ , .u , kv
cos
k k v = 1
n v
k k u = 1
JL.
k k t = 1
(
k
2 kt n t T t
k
k
T u
cos
( 2 k v n v
A
cos
+ Е Е Ес, , k. , kv
cos
2 kt n t
k
k
2 ku n u
T u
k
k
sin
k k v = 1 ( nv
k k u = 1
( Jvv
k k t = 1
(
+ Е Е Е d k. , ku , kv
cos
T k Lt 7
,(2 k t nt 1
sin
k
2ku n u
T u
k
k
cos
k k v = 1
( n v
k k u - 1 ( nvv
k k t = 1 ( nv.
+ Е Е Е e k. , k. , kv
sin
T k Tt 7
2 k n t
sin
k
7-
2 ku n u
T u
A
k k v = 1 ( n v
k k u = 1 ( nvv
k k t = 1
( _ n_
k
T t
cos
+ Е Е Е f t , k. , kv
sin
k k v = 1 ( n v
k k u = 1 ( nv.
k k t = 1
( 7-
k
2 kt n t T t
A
k
cos
+ Е Е Е& , t u , kv
sin
2 kt n t
A
k k v = 1
7 n v
k ku = 1
k k t = 1
( n v ( n v
k
+ Е Е Eh
k k v = 1
k k u = 1 k k t = 1
1 kt , ku , kv sin
Tt 7
2 kt nt '
sin
T k Tt 7
2 ku n u
T u
k
sin
T
T v 77
2 k n v 1
v 77
7 k
7 k
+
+
k
sin
k
k
cos
2 ku n u
T u
k
k
sin
2 ku n u
k
k
2kv n v 1
v 77
2-^ 11
T v 77
2 k v n v T
T v 77
^kv n v 1'
v 77
7 k
7 k
7 k
7 k
7 k
7 k
7 k
+
+
+
+
T k u 7
(2к nui k Tu 7
cos
k
sin
2 kv n v T v
2 kv ^ v 11
T k v
k
7 k
+
k
k
,
где A, B, a, b, c, d, e, f, g, h - коэффициенты разложения Q(t, u, v) в пятикратный ряд Фурье по переменным – времени, осадкам за год и вегетационный период, двух географических координат (рис. 3).
|
время (t) осадки за год (u) за вегетационный период ( ) |
----► |
Инфицирован ность почвы ( Q ) |
Рис. 3. Изменение запаса инфекции в почве
Выводы
-
1. Наиболее перспективен метод математического моделирования определения тенденций развития продуктивного процесса. Поэтому разработка моделей дает возможность, используя статистические данные, проследить закономерности выпадения осадков, тепловой режим, координировать сроки сева, изменять структуру севооборотов и на основе этого получать высокие и устойчивые урожаи, при этом существенно сократить экономические затраты.
-
2. Модельная оценка запаса инфекции в почве является важнейшей составляющей для планирования мероприятий по защите растений с учетом временной и природно-экологической структур.
-
3. Разработанные модели рекомендуется использовать для обоснования и планирования эффективного производства зерновых культур в агроэкологических зонах Красноярского края в зависимости от запаса инфекции в почве.


