Модели особенностей теплового сопротивления кристаллов с фазовыми переходами и дефектами

Тепловые и электрические свойства сегнетоэлектрических, сегнетоэластических кристаллов и полупроводников типа А2В6 при низких температурах отличаются крайне высокой чувствительностью к наличию в их кристаллической решетке (матрице) структурных фазовых переходов (СФП), дефектам, примесям или их комплексам (кластерам, доменам и наноструктурам). Вместе с тем, реальный кристалл с дефектами и фазовым переходом (особенно вблизи температуры СФП Т = Тс ) представляет собой весьма сложную физическую систему, не допускающую пока еще строгого теоретического описания [1-5, 17]. К тому же в последнее время появились новые весьма интересные данные по аномальному поведению теплопроводности К(Т) для ряда сегнетоэлектрических (KDP) и сегнетоэластических (Hg2Cl2) кристаллов [6-9]. На кристаллах селенида цинка легированных никелем (ZnSe: Ni), кристаллах ZnSe: Fe (а также Zn1-xFexS) обнаружено ги-гантское возрастание (на два порядка и даже более чем в 200 раз) теплосопротивле-ния (W) с максимумами при Т=15 К и Т=20 К соответственно [10-13]. Несмотря на значительные успехи в области технологий выращивания отмеченных выше кристаллов и материалов микроэлектроники, разработка приборов и структур на их основе зачастую сдерживается из-за отсутствия надежного описания, численных расчетов, математического моделирования и должной интерпрета- ции физических свойств этих материалов.

В настоящей работе представлены результаты математического моделирования механизмов рассеяния фононов и тепловых свойств материалов твердотельной микроэлектроники: сегнетоэлектрических (эластических) кристаллов KH₂PO₄, Hg₂Cl₂; SnTe, GeTe (А₄В₆) и полупроводников типа А₂В₆. Рассмотрены: модели температурной зависимости теплопроводности кристаллов с фазовым переходом, флуктуационный эффект биений различных каналов рассеяния фононов, модель гигантского теплосопротивления ( W ₌ K ^{- 1} ) в легированных кристаллах типа А₂В₆.

Моделирование поведения теплового сопротивления реальных кристаллов около Т_с Теплопроводность систем с фазовыми переходами и дефектами.

Критические показатели

Для коэффициента теплопроводности (К) гармонического кубического кристалла с примесями или дефектами (кластерами, коллоидами, доменами) ранее была получена формула типа Кубо-Гринвуда [4,5]:

∞ 22

K(T ) =       I.... ⁿ ( ^ )[ ⁿ( ® ) + 1] Sp I П( ® ) I² d ® ;(1)

6 π k   T ² V

Б ^-∞

Пρ(lli′ω)=∑Qρ(ll′′)ImD(l′′li′ω), (1а) l′′ где V – объем кристалла; Q – величина, связанная с массами и силовыми постоянными атомов в узле l кристаллической решетки; D(w) – функция Грина реального кристалла с гамильтонианом Н.

При наличии в системе фазового перехода, используя уравнение Бете-Солпитера для корреляционной функции ток-ток [1,14] можно получить рекуррентные формулы (соотношения) для траекторий гамильтониана U(l), r(l) , определить при малых s = 4 - d ( d -размерность пространства) положение неподвижной точки ( U _*, r _* ) и критические индексы поведения системы при Т >  Т с . Такой подход позволяет найти численные значения критических показателей параметра порядка (поляризации) ( β ), восприимчивости ( γ ), корреляционной длины системы ( v ), внешнего поля ( δ ), корреляционной функции ( η ) и теплоемкости ( α ) [15, 16]:

в = 0,334, Y = 1,166 , v = 0 , 583,

5 = 4,50, п = 0 и а = 0,166.

В результате анализа экспериментальных данных по теплопроводности К(Т ) и сравнения этих данных с результатами расчетов [1] авторам удалось найти критический индекс Y = а + zv ( z - динамический показатель корреляционной функции ток-ток), определяющий поведение сечения поглощения звука около T ₀ . Найденное значение у = 1 совпадает с результатом для свободного (среднего) поля, где в соответствии с гипотезой подобия _а = 0, v = 1/2 и тогда z = 2. Однако, в точке T = T c >  T ₀ значение ю₀ часто не об-ращает ся в ноль и особенность K ( T ) может оказать-ся “затушеванной”. Кроме того, критический индекс z в случае релаксационной динамики

нетоэлектриков-полупроводников (SnTe, GeTe [4, 5]) около T_c с учетом значений показателей (по теории свободного поля Ландау) у = 1 и _v = 1 / 2, получаем р = 1 ^ 1 , 25 и z = 2, близкое к полученному выше результату z = 2 , 096.

Расчет теплопроводности К(Т)в модели Дебая

Для расчета температурной зависимости K ( T ) в простой дебаевской модели кристалла с фазовым переходом с учетом (1) получаем [4, 20]:

К ( Т ) = а

f -)2

VT У

■I

л x — xeT

e

^

— 1

1 γ ( х )

dx , (2)

V У

где α – коэффициент при интеграле теплопроводности, связанный с квадратом скорости фононов; θ – характеристическая температура кристалла (температура Дебая); γ ( x ) – сумма обратных времен релаксации, обусловленных рассеянием фононов в исходном (“идеальном”) кристалле ( γ ₀), за счет механизмов структурного фазового перехода ( γ_С ), дефектов и их комплексов ( γ_k ) и за счет резонансного рассеяния на примесях ( γ_r ).

Для описания обратного времени релаксации, обусловленного рассеянием фононов на коллоидах (наночастицах) с радиусом r и концентрацией N можно воспользоваться следующим выражением [5, 13, 21]:

можно определить [14] в виде ^z = ² + 2 П (такое же выражение, но другим способом было получено в [17]), что по своему значению близко к результату s -разложения z = 2 + сп

( с = ⁶ ln 3 - ¹ » 0 , 73) и к значению z = 2 , 095 ± 0 , 008, полученному методом Монте-Карло [18] для однородной системы. В то же время согласно теории подобия [14,19]

Y _k(x,r,N) = N ■ M ■ r ² ■<

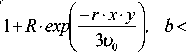
1 D \ — Ь 1+R ■ exp I— r ■ x ■ y

υ ₀

r ■ x ■ У .

υ ₀

, b >

r ■ x ■ y

υ ₀

.

Здесь R– параметр, зависящий от упругих свойств коллоида и матрицы; b – постоянная, связанная с r ; М = п ■ v ₀ ■ 10³; и ₀, у , х – приведенные скорость, температура Дебая и частота фонона соответственно; x = ^to _D , to _D = к Б О / к -дебаевская часто та кристалла; k_Б – постоянная Больцмана.

,Y—Р z = 2 +--и по данным опытов и расчетов температурного поведения проводимости сег-

Флуктуационный эффект биений в сегнетоэлектриках (эластиках)

В результате оптимального подбора параметров теории и модельных расчетов по

формулам (2) и (3) нами были сопоставлены данные теории и опытов для систем Hg2Cl2 и типа KDP (KH2PO4) и показано, что вблизи Tc в кристаллах типа KDP в целом ведущую роль играет квазиупругое рассеяние фононов γc (x) . Однако рассеяние на комплексах (коллоидах, доменах) – наноструктурах γk(x), наиболее интенсивно образующихся около температуры Tc , определяет условия появления и характер флуктуационного эффекта биений различных каналов рассеяния фононов. Для кристаллов типа KDP (ТС = 122К = Т3 = 121,99К) удалось подтвердить предположение о том, что “флуктуационный эффект биений” различных каналов рассеяния фононов приводит к особому поведению теплового сопротивления K(T) вблизи Tc в виде излома, полочки или весьма узкого пика ( yt = Т3 — Т2 * 0,2 ^ 0,3 К -максимум) на фоне широкого спада, прогиба или провала около Tc . В случае Hg2Cl2 наблюдается довольно широкий YT * 6 —10K несимметричный максимум, расположенный в области широкого AT * 80 -100K провала (критической аномалрии) с температурой фазового перехода Tc = 186K (рис. 1). Отметим, что на кристаллах триглицинсульфата (ТГС) в области температур AТ * 3 К около Тс при Т > 9 [6,7] наблюдается яркая узкая особенность (типа “провал”), видимо обусловленная эффектом “флуктуационных состояний” (или биений), требующая однако отдельного рассмотрения.

Таким образом, формулы (2) и (3) моделируют характер флуктуационного эффекта биений в кристаллах типа KDP, Нg₂Cl₂ (ТГС) и подтверждают его флуктуационное происхождение, определяя условия и область ДТ его проявления. В кристаллах Нg₂Cl₂ в частности в интервале A Т = 0 , 5 ° К около Т с возможны неустойчивые (метастабильные) состояния [22, 23]. Здесь важную роль играет соотношение времен релаксации фононов, связанных с кластерами γ_k (доменами) и цен-

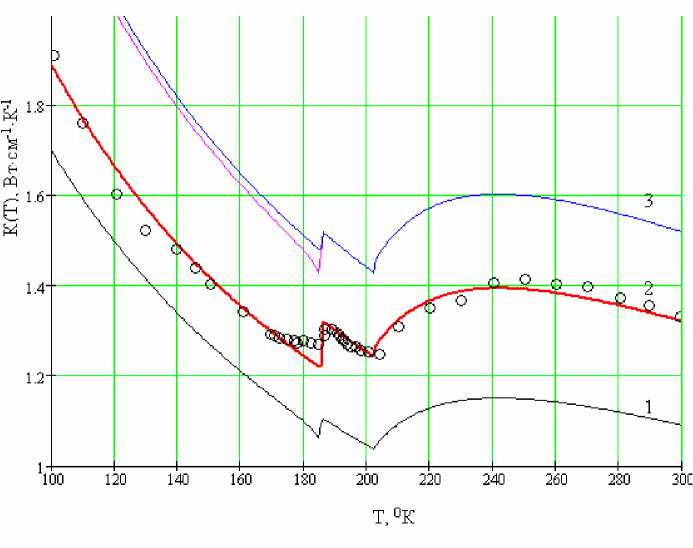
Рис. 1. Температурная зависимость теплопроводности кристаллов Нg₂Cl₂ [6-8] Сплошные линии – результаты расчетов:

кривая 1 смещена вниз для наглядности - число коллоидов N 1 = 0 ,95( - 10¹⁴ см ³ ) и N ₂ = 0 , 98

при T >  T c = 186 0 K и T <  T c соответственно (при T >  205⁰ К , Y c >  Y k ); 2 - N 1 = 0 , 98 и N 2 = 1 , 2 ;

кривая 3 смещена вверх - N 1 = 0,98 (T > Tc) и N2 = 1,05 (или N2 = 1,07 , Yc > Yk для 1800 К < T < Tc) при T < Tc

тральным пиком γ_с . При этом сравнение результатов расчетов с данными опытов показывает, что кластеры (коллоиды) наиболее интенсивно образуются в достаточно широкой области температур (20 – 30 ^оК) около Т_с. При переходе в низкосимметричную фазу происходит резкое незначительное увеличение их числа и затем концентрация кластеров уменьшается при т ^ 0 .

Таким образом, предложено модельное описание рассеяния фононов на точечных дефектах кристаллической решетки, на их комплексах, кластерах-наноструктурах и в целом развит подход к анализу влияния дефектов, кластеров (доменов), наночастиц на критическое поведение теплопроводности кристаллов около Тс на микроскопическом уровне.

Гигантское теплосопротивление в легированных кристаллах типа А2В6 В последнее время появились новые ин- тересные данные по аномальному поведению кривой теплопроводности K(T) для ряда кристаллов с нанокластерами, с комплексами дефектов, с коллоидами, другими возмож-ны-ми пространственно-коррелированными образованиями (системами), или со структурными фазовыми переходами. В частности, как было сказано во введении, на кристаллах селенида цинка (ZnSe: Ni) легированных никелем и кристаллах ZnSe: Fe недавно обнаружено гигантское теплосопротивление с максимумами при Т=15 К и Т=20 К соответственно [10-12]. Подобные явления наблюдаются на кристаллах НgSе: Fе с пространственно-коррелированной системой ионов железа [13].

Для описания обратного времени релаксации ( т Г = Y_r ), определяющего резонансное рассеяние фононов на примесях можно использовать следующее выражение [5]:

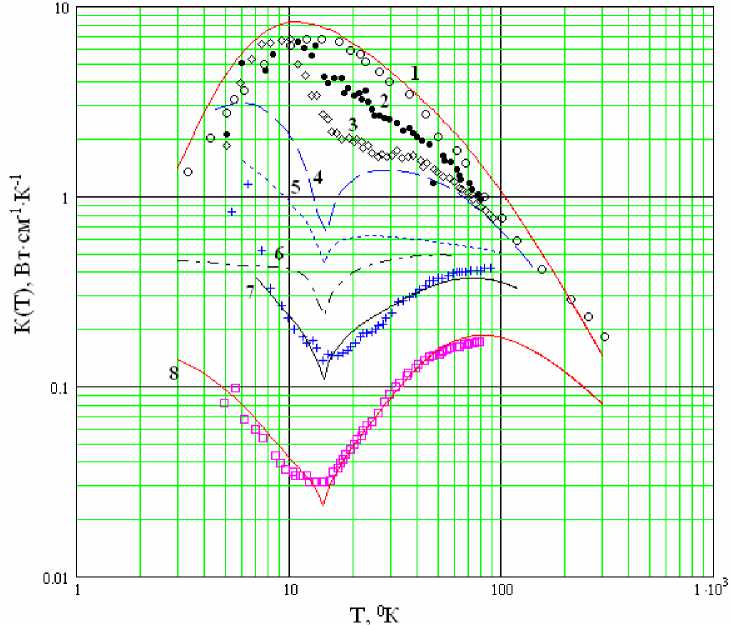
Рис. 2. Температурная зависимость теплопроводности кристаллов ZnSe: эксперимент [10,11]. Обозначения (сверху вниз) 1,2 – чистый ZnSe; 3,7,8 – образцы ZnSe:Ni с различной концентрацией никеля: 3 – c ₀ = 0 . 00043 (10 21 cm^-3 ) , 7 - 0.036 , 8 - 0,10 . Результаты расчетов: для чистого кристалла (кривая 1); 4 - с фазовым переходом y _c ^ 0 , T_c = 14 • 5 0 K ; 5 — Y_c ^ 0 , Y r ^ 0 ( ^с о = 0 • 005 ); 6 — Y k ^ 0 , число коллоидов N = 10¹⁴ cm ^{- 3} ; 7 и 8 - величины Y_c и Y r подобраны в соответствии с данными опытов.

„-1 _{= n}        c 0 • D 0 ^^r 0 • ( xy ) 2 2

r = py*(x ² - x 2 ) ² + Г 2 (xy)² n • ²

• 10 8 c ^{- 1} . (4)

Здесь с₀ – концентрация примесей или дефектов (систем), ro D = yp ( p = 10¹³ с^-1, Г ₀ = 6, D ₀ = 1 , 21 • 10⁶), n = 4 или 1,2,3 и зависит от характера рассеяния фононов на резонансной частоте x ₀ = ro ₀ Ig>_d , связанной с примесью, дефектом, с туннельными (спиновыми) уровнями или другими фононными резонансами (например, двухуровневые системы в спиновых стеклах).

Формулы (2) – (4) со скоростью релаксации y = Y о + Y _c + Y k + Y r (выражения для γ ₀ и γ_c были взяты согласно [1, 4]) использовались для расчетов кривой K ( T ) кристаллов ZnSe ( 0 = 280⁰ K ) сильно легированных никелем. Результаты расчетов сопоставляются с данными соответствующих экспериментов (рис. 2).

Рассчитанные кривые K(T) в целом качественно согласуются с поведением кривых теплопроводности исследуемых кристаллов. Однако, в теории слабо обозначены заметные на опыте перегибы на кривых 3 и 7 в области 17 - 300 К, связанные с yr. Еще менее заметны резонансы при т = 9 - ц0 к на кривых 7 и 8. Эти резонансы (справа и слева) слабо выражены, поскольку расположены непосредственно около минимумов теплопроводности (кривые 7 и 8), связанных с фазовым переходом при Тс = 14,50 К , наблюдающимся также на кривых 2 и 3. В теории влияние γс вблизи Тс несколько заметнее, чем на опыте, а положение минимума на кривой К(Т) смещено на 0,5 -10 К вправо относительно Тс. Значительное расхождение теории с экспериментом имеет место на кривых 7 и 8 при Т < 60 К. Возможно это связано с неоптимальным выбором параметров скоростей релаксации фононов на комплексах дефектов (коллоидах) γk и на границах образцов кристаллов. Однако, поведение кривых К(Т) в области низких температур ( т < 60 К) требует отдельного рассмотрения, тем более что при Т < 60 К на опыте на всех кривых имеется всего одна-две точки. Отметим, что развитая в работе теория удовлетворительно описывает поведение теплопроводности ZnSe:Ni, а подобранные в ходе вычислений параметры времен релаксации фононов от- вечают физически обоснованным представлениям о характере рассеяния тепловых фононов и стадиях дефектообразования, реализующихся в кристаллах типа А2В6 по мере их легирования [21].

Обсуждение и выводы

На основе формул типа Кубо-Гринвуда получено выражение, позволяющее рассчитать теплопроводность сегнетоэлектрических (эластических) кристаллов и полупроводников типа А2В6 на микроскопическом уровне. Предложены новые методы и модели для расчета тепловых свойств сегнетоэлектриков (эластиков) и кристаллов А2В6; проведен численный анализ влияния различных механизмов рассеяния фононов на температурную зависимость теплопроводности этих материалов. Таким образом, в работе:

• -    разработана теория и построена модель флуктуационного эффекта биений и температурного поведения теплопроводности сегнетоэлектриков типа KDP (KH₂PO₄), ТГС (флуктуационные состояния) и сегнетоэластиков Hg₂Cl₂ вблизи структурного фазового перехода. Для кристаллов типа KDP удалось подтвердить предположение о том, что “флуктуационный эффект биений” различных каналов рассеяния фононов приводит к особому поведению теплового сопротивления K ( T ) вблизи T_c в виде излома, полочки или весьма узкого пика ( у_Т « 0 , 2 ^ 0 , 3 К - максимум) на фоне широкого спада, прогиба или провала около T_c . Путем изменения величин управляющих параметров системы появляется возможность реализации различного температурного поведения теплового сопротивления и условий проявления эффекта биения;

• -    дано объяснение эффекту гигантского теплосопротивления, обнаруженному в широкой области температур T = 10 ^ 30 0 K в легированных кристаллах ZnSe. Использованные при вычислении кривых К(Т) и s(Т) параметры времен релаксации носителей отвечают физически обоснованным представлениям о характере рассеяния тепловых фононов в легированных кристаллах ZnS и ZnSe.

Вместе с тем, в работе достигнуто качественное вполне приемлемое соответствие теории и эксперимента, которое имеет место для всех проведенных расчетов.

В заключение авторы выражают признательность коллегам В.П. Сахненко, А.С. Си-гову, Б.А. Струкову и С.А. Садыкову, обсуждавшим результаты настоящей работы и сделавшим ряд полезных замечаний по ходу ее оформления.