Модели с неопределенной волатильностью

В 1965 году П. Самуэльсоном в работе [1] была предложена модель геометрического броуновского движения. Именно она легла в основу модели Блэка – Мертона – Шоулса, с которой связана знаменитая формула Блэка и Шоулса для рациональной стоимости стандартного опциона-колл европейского типа, полученная в 1973 году в работах [2, 3]. Под рациональной стоимостью понимается минимальная величина начального капитала, которая дает продавцу опциона возможность построения хеджирующего портфеля. Оригинальный вывод формулы Блэка – Шоулса основан на решении фундаментального уравнения с краевым условием. Поскольку полученное фундаментальное уравнение относится к уравнениям типа Фейнмана – Каца [4], оно может быть решено стандартной техникой решения таких уравнений, а именно, сведением к уравнению теплопроводности путем введения новых переменных. Мар-тингальный вывод формулы Блэка – Шоулса основан на том, что в рассматриваемой модели (B,S)-рынка существует единственная мартингальная мера. Это определяет безарбитражность рассматриваемой модели и дает возможность рассчитывать рациональную стоимость опциона как математическое ожидание по мартингальной мере от дисконтированного финансового обязательства. Цена, полученная в результате оригинального или мартингального подходов, является справедливой ценой, так как если назначаемая цена опциона меньше полученной цены, то продавец опциона не сможет выполнить свои контрактные обязательства; а если назначаемая цена опциона больше полученной цены, то продавец заведомо будет иметь чистый доход.

Модель Блэка – Шоулса – Мертона имеет ряд недостатков. В частности, в ней предполагается, что параметры модели (процентная ставка, снос и волатильность)

являются постоянными. В этом отношении следует отметить так называемый смайл-эффект [4], который не объясняется стандартной (B,S)-моделью. Суть смайл-эффекта заключается в следующем. Формула Блэка – Шоулса дает явную зависимость рациональной стоимости опциона C (a, T, K ) от волатильности а, момента исполнения T и контрактной цены K . Можно, однако, обратиться к реально существующим на финансовых рынках стоимостям этих опционов C (T, K ) с заданными T и K и сравнить их с теоретическими значениями. Найдем a (T, K ) как решение уравнения C (a,T,K ) = C (T,K ). Величина a(T,K ) называется предполагаемой волатильностью. При фиксированном K величина a (T, K ) меняется с изменением T . При фиксированном T величина a (T, K ) также меняется с изменением K , будучи выпуклой функцией (это и объясняет название смайл-эффект). Смайл-эффект является тем фактом, который не объясняется стандартной (B,S)-моделью, что привело к разнообразным ее обобщениям и усовершенствованиям.

В 1993 году в работе [5] была предложена модель Хестона. В модели Хестона цена акции и волатильность описываются стохастическими дифференциальными уравнениями с винеровскими процессами W ¹ и W ² такими, что dW _t1 dW _t2 = pdt. В работе [6] приведены различные разностные схемы для модели Хестона. Недостатком данной модели является неединственность мартингальной меры, что, в свою очередь, означает отсутствие справедливой стоимости опциона. Интервал справедливых цен заменяет справедливую цену в этом случае. Поскольку волатильность в модели Хестона – неограниченная величина, то интервал справедливых стоимостей может оказаться непригодным при выборе начальных инвестиций. Например, при совпадении страйка европейского опциона колл с начальной стоимостью рискового актива и при постоянной стоимости безрискового актива интервал справедливых стоимостей будет иметь вид: [0, S o ], S 0 — начальная стоимость рискового актива. Очевидно, что данный интервал совершенно непригоден для принятия решения. В настоящей статье рассматривается реализация модели Хестона, позволяющая для заданной траектории волатильности получать единственную мартингальную меру, а значит, и единственную стоимость опциона, зависящую от траектории. Такая параметризация мартингальных мер позволяет использовать метод Монте-Карло для вычисления интервала справедливых стоимостей. Другим средством вычисления интервала справедливых цен является вычисление с заданной вероятностью доверительного множества траекторий волатильности, что, естественно, приводит к моделям с неопределенной волатильностью. Поэтому основной целью данной статьи является продолжение и развитие моделей и методов, изложенных в работе [7].

Модели неопределенной волатильности впервые были изучены в [8–14]. В работах [8, 12] неопределенная волатильность представляет собой семейство детерминированных траекторий. В данной статье рассматривается обобщение модели Блэка – Шоулса, заключающееся в том, что волатильность σ заменяется на интервал с границами, не зависящими от времени ([а, а]) и зависящими от времени ([а,Of]). В результате получается неполный рынок, а фундаментальное уравнение Блэка – Шо-улса заменяется на два уравнения, не имеющих аналитических решений. Полученные уравнения называются вязкостными уравнениями Гамильтона – Якоби – Беллмана [15], а их численные решения определяют интервал справедливых цен. В статье предложены три вычислительных метода нахождения интервала справедливых цен. Первый метод основан на решении вязкостных уравнений с использованием разностных схем. Вторым является метод Монте-Карло, который основан на моделировании исходного процесса стоимости акции. В связи с этим следует отметить алгоритмы генерации зависимых нормальных и бинарных случайных величин. Третьим является метод деревьев, который основан на аппроксимации исходной непрерывной модели дискретной моделью и получением рекуррентных формул на бинарном дереве для расчета верхней и нижней цен. В статье присутствуют результаты расчетов интервала справедливых цен с использованием трех вышеперечисленных методов. Совпадение полученных результатов является, по мнению авторов, хорошей верификацией предложенных методов.

1.    Модель Блэка – Шоулса

Рассмотрим модель Блэка – Шоулса [4], в которой стохастический дифференциал дисконтированного процесса стоимости акции t , а также дифференциал банковско-Bt го счета имеют вид:

d — t = —t adW _t , dB _t = B t rdt.                        (1)

B t   B t

S t

Из (1) следует, что процесс _B является мартингалом относительно исходной меры

P . Процесс —t можно записать в виде —t = —0 exp (-- t + aW _t ), откуда следует,

Bt         2               Bt   Bo     \ 2        / что St = So exp ^ ^r —^ t + aWt^ . Обозначим

Y t =

f r — ^Л t + aW t , Y o = 0.

Из (2) следует, что dY t

r —2^ dt + adWt. Введем функцию U (t, Yt), которая выражается через платежное обязательство f (YT) согласно следу- ющей формуле:   exp (—rt) U (t,Yt)

E (exp (—rT) f (Yt) /Ft). Введем функ- цию U (t, Yt) = exp (—rt) U (t,Yt), из формулы Ито [4] следует, что dU = exp (—rt) ( —-rU + U‘ + rr — ^2-^ Uy + ^2-Uy’y^ dt + UyadW).

В силу того, что процесс E (exp ( — rT) f (Y T ) /F _t ) является мартингалом по исходной мере P , коэффициент при dt в выражении для dU должен быть равен 0, откуда следует уравнение теплопроводности

r — _TJ U y + T ^U^y — rU = ⁰

с краевым условием U (T,y) = f (y).

Приведем процесс Y n , аппроксимирующий процесс Y t из (2):

AY n = (r — 02-^ h + aVhE n , h = T, n = 1,..., N.

Последовательность (e n ) N =1 состоит из независимых стандартных нормальных случайных величин, N - число разбиений интервала [0, T]. В данной модели мартингаль-ная мера не является единственной.

Пользуясь приемом, изложенным в [16], приведем бинарную модель, аппроксимирующую модель (4):

A’Y n = aVhS_n,n =1,...,N.                          (5)

Последовательность (d n ) N =1 состоит из независимых радамахеровских случайных величин, принимающих значения 1 и — 1, вероятность p = P (5 n = 1) = ^ +

(■ -

h

2а

. Для бинарной модели мартингальная мера единственная; введем функцию U (n,y) = (1 +   N-nE ff YNn) /Yn = y). Для этой функции справедливы следующие рекуррентные формулы:

U (n — 1, y) =       E (U (n y + ^AY n ) /Y n - 1 = y) =

1 + rh

1 + rh

(pU (n, y + aVh^ + (1 — p) U (n, y — a V h)) , U (N, Y n ) = f ( Y n ) .

Цена европейского опциона U (0,0) с платежным обязательством f (Y T ) = max(S ₀ exp(Y T ) — K, 0) может быть также рассчитана с помощью формулы Блэка -Шоулса:

U (t, Y t ) = S o exp (Y , ) Ф

—K exp ( — г (T — t))Ф

*In K + Y , + (T — t) (г + y^ aVT — t

* In K + Y , + (T — t) (г — ₂ )' aVT — t

-

ф (y) =

2n

/Lexp (—fl

dx – функция Лапласа.

Еще одним способом вычисления цены европейского опциона U (0, 0) обязательством f (Y T ) является метод Монте-Карло:

с платежным

U (t, Y , ) » ^exp( MT t)) £ f ( y , + (г — у ) (T — t) + a V T — t E i ) ,      (8)

M - количество экспериментов, (s i ) M 1 - последовательность независимых стандартных нормальных случайных величин.

Пример 1. Пусть г = 0,1, a = 0,05, S 0 = 5, T = 1, M = 1000. В табл. 1 приведены значения цены европейского опциона U (0, 0) с платежным обязательством f (Y T ) = max(S ₀ exp(Y T ) — K, 0), рассчитанные с помощью решения краевой задачи (3), применения рекуррентных формул (6), а также с использованием формулы Блэка – Шоулса (7) и метода Монте-Карло (8).

На рис. 1 приведен график зависимости значений U (0, 0) от N при K = 5 для рекуррентных формул, из которого следует, что параметр N достаточно взять равным 20. На рис. 2 приведен график зависимости значений U (0, y) от y при K = 5 для краевой задачи.

Таблица 1

Зависимость справедливой цены от контрактной цены в модели Блэка – Шоулса

K	Решение краевой задачи	Формула Блэка – Шоулса	Метод Монте-Карло	Рекуррентные формулы на бинарном дереве
1	4,0948	4,0952	4,0909	4,0949
2	3,1895	3,1903	3,1860	3,1899
3	2,2842	2,2855	2,2812	2,2848
4	1,3790	1,3807	1,3763	1,3797
5	0,4765	0,4778	0,4742	0,4767

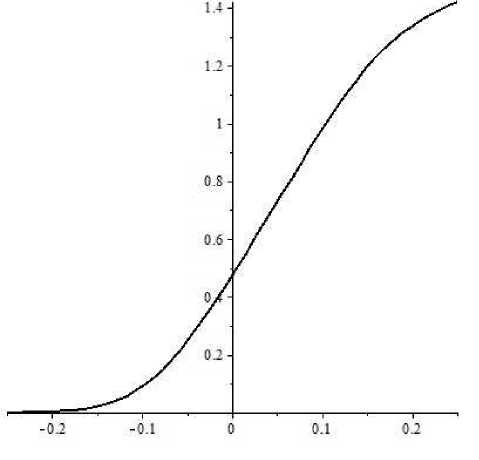
Рис. 2. Зависимость значений U (0, у) от y в модели Блэка – Шоулса для краевой задачи

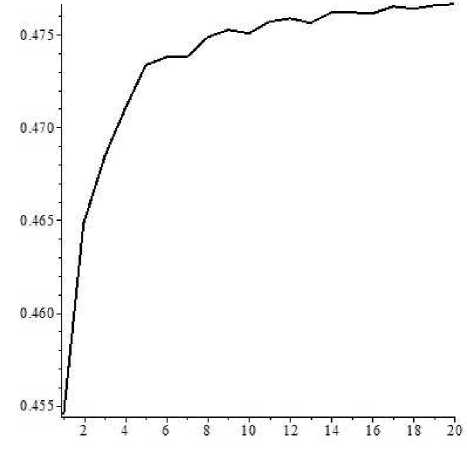
Рис. 1. Зависимость значений U (0, 0) от N в модели Блэка – Шоулса для рекуррентных формул

2.    Модель Хестона

Рассмотрим реализацию модели Хестона [5], в которой стохастический дифференциал дисконтированного процесса стоимости акции ^t имеет вид:

B t

S t     S t

B t    B t

V t dW _t ¹ .

S t

Из (9) следует, что процесс _B является мартингалом относительно исходной меры

P . Процесс ^t можно записать в виде: ^t

B t                           B t

- B exp (-2 / t V^dT+/ '

откуда следует, что S t = S _o exp

(rt - 2 / t

V _T dT +

t

. Обозначим

Y t = rt —

• 1    Г t

• 2    Л

V _T dT +

t

dW , . Y o = 0.

Отсюда следует, что dY t =

(r - В

dt + VV-dW t ¹ . Предположим, что волатильность

является процессом квадратного корня:

dV = k (0 — V t ) dt + aVVtdW t .

Процессы W t ¹ и W 2 являются винеровскими с dW^dW² = pdt. Введем функцию U (t,Y t ,V t ), которая выражается через платежное обязательство f (Y T ) согласно следующей формуле: exp ( — rt) U (t,Y t ,V t ) = E (exp ( — rT ) f (Y T ) /FY^V ).

Введем функцию   U (t,Y _t ,V t )

exp ( — rt) U (t,Y _t ,V t ),   тогда dU

^exp ^{( — rt)    — rU} + ^U t + (^{r —} V^ U y + k ^{(0 — V} ) U V + V U yy +

σV

^U VV + U y ’ v ^{V ap}j ^dt+

U y W dW 1 + U V a ^ VdW ² ). В силу того, что процесс Е (exp ( — rT ) f (Y T ) /F YV )

яв-

ляется мартингалом по исходной мере P , коэффициент при dt в выражении для dU должен быть равен 0, откуда следует уравнение

—rU + U ‘ + (r^— —^ U y + k ^{(0 —} V ) U V + — U y ’ y +— 2— U VV + U yV ^Vap = ^{0     (12)}

с краевым условием U (T,y,v) = f (y ). Цена опциона U (0, 0,v ₀ ). Приведем дискретную модель, аппроксимирующую модель Хестона:

AYn = ^

AV n = k

^r —2™^ h ⁺ V V n - i h^ n , ^{(0 —} V n - 1 ) h + ^aVVn-l-h^^-Tii

Y o = 0, V o = v o ,n = 1,...,N.

Последовательности (6n)N=1 и (6n)N=1 состоят из нормально распределенных случайных величин с Е^П = 0, Е^П = 0, E (еП)  = 1,E (еП)  = 1,E (еПеП) = р. Пользуясь приемом, изложенным в [16], приведем бинарную модель, аппроксимирующую модель (13):

Г AY n = VV n -i hd 1 ,

I AV = aVV - h^ n ,                       (14)

Y o = 0, V o = v o ,n = 1,...,N.

Последовательности (5 n ) N =1 и (5 n ) N =1 состоят из независимых радамахеровских слу-

чайных величин,

2 +

r

-

V n - 1

)

принимающих значения

1 и — 1, вероятности p 1 = P (^ = 1) =

h

2 Vk-7

, p 2

P (^ n = 1) =

+

k θ - V n - 1    h

2aV^- i

cov δ _n ¹ , δ _n ²

ρ .

Таблица 2

Зависимость справедливой цены от контрактной цены в модели Хестона

K	Решение краевой задачи	Метод МК, аппроксимация бинарными с.в.	Метод МК, аппроксимация нормальными с.в.
1	4,0747	4,0844	4,0980
2	3,1718	3,1795	3,1932
3	2,2853	2,2763	2,2883
4	1,4619	1,4332	1,4037
5	0,7617	0,7604	0,7106

Введем функцию U (n, y, v) =

(1 + rh) N - n

U (°, °, v o ) =       aw E f Y n /Y o = °, V o

(1+ rh) N

E ff (Yn) /Y n = y, V n = v). Цена опциона = v₀) может быть рассчитана с помощью

метода Монте-Карло. Для дискретной аппроксимации (13) необходимо в каждом эксперименте генерировать случайные величины ε ¹ _n , ε ² _n согласно следующему правилу.

Сначала генерируются независимые, стандартные нормальные случайные величины

E n ,E n Затем е П := е П ,е П : = е П р + е П^ 1 — р ² . Для дискретной аппроксимации (14) необходимо в каждом эксперименте генерировать случайные величины δ _n ¹ , δ _n ² согласно следующему правилу. Сначала генерируется случайная величина δ _n ¹ с вероятно-

стью p i = P ⁽^ П = 1) = 2 +

(Г — V-)

------,    ---. Если 5 1 = 1, то случайная величина 5 2 2 _ХГ                 n                                  n

генерируется с вероятностью P (§ П = 1/5П = 1) = — + p ₂ . Если 5 П

p 1

величина 5 П генерируется с вероятностью P (5 n = 1 /5 П = °) = р ₂

-

= °, то случайная

ρ

.

1 — p 1

Пример 2. Пусть р = °, 1, v ₀ = °, °5, S 0 = 5, T = 1, k = °, 25, 6 = °, 25, р = °, 5, N = 2°, M = 1°°°. В табл. 2 приведены значения цены европейского опциона с платежным обязательством f (Y T ) = max(S o exp(Y T ) — K, °), рассчитанные с помощью решения краевой задачи (12), а также с использованием метода Монте-Карло для случая аппроксимации нормальными и бинарными случайными величинами (формулы (13) и (14) соответственно).

3.    Две модели с неопределенной волатильностью В этой части мы рассмотрим следующую тива: модель изменения цены рискового ак- St = So exp (Yt) ,dYt = ^r - ^2^ dt + atdWt-

Неопределенная волатильность удовлетворяет следующим неравенствам:

σ _t ≤ σ t ≤ σ t .

В неравенствах (16) функции σt и σt являются детерминированными функциями. Пусть множество Atl = {at : at < at < at, t E [t1, t2]}. Чтобы оценить верхнюю и нижнюю цены, нам необходимо решить следующие задачи стохастического оптимального управления:

sup E „ f ( Y t ), inf E „ f ( Y t ).

σ ∈ ∆ 0 ^{T             σ ∈ ∆} 0 ^T

Введем функции v (t, y) = exp (-r (T - t)) sup E (f (Yt)/Yt = y), v (t, y) = σ∈∆tT exp (-r (T - t)) inf E (f (Yt) /Yt = y), тогда верхняя цена V = v (0, 0) и нижняя цена σ∈∆tT

V = v (0, 0). Уравнения Гамильтона - Якоби - Беллмана для функций v (t, y) и v (t, y) имеют следующий вид:

v t + rv y + sup v ⁽v y ‘ y ^- v y ) = rv, ^ t < CT < CT t ²

σ ²

v t + rv y + inf —( v yy ^- v y ) = rv £ _t <^CT<^CT t 2

с краевыми условиями v (T, y ) = v (T, y) = f (y ). Эти уравнения эквивалентны следующим уравнениям:

^v t + ^{(r —} A t ) v y + A t v yy + B t v' yy v t + ^{(r —} A t ) v y + A t v yy - B t v yy

= rv,

= rv,

CT 2 + CT 2        a 2 -

A * =     , ' ,b* = "^£T

Уравнения (19) являются уравнениями G-теплопроводности с нелинейными операторами:

G 1 ^(t, v y ’ ^v yy ) = A t ^{( v} yy ^- v y ) + B t v yy ^- v y I ’

G 2 ^(t, v y , ^v yy ) = Mv yy ^- v y ) ^- B t ^{| v} yy ^- v y | .

Если функция f (y) непрерывна и ограничена, At и Bt являются непрерывными функциями на интервале [0,T], то уравнения (19) имеют единственные вязкостные решения [5]. Верификация Перрона вязкостных решений (19) как решений задач стохастического оптимального управления (17) является стандартной [17]. В финансовой литературе уравнения (19) известны как уравнения Баренблота [11], когда At и Bt являются константами.

В первой модели dat = natdt, то есть ст* = Uo exp (nt), неопределенный па-ст2 (exp(2nt) + exp (2nt)) раметр n £ [n,n], ст0 - начальное условие. Тогда At = ------------^, ст2 (exp(2nt) - exp (2nt))

Bt = -----------^. В симметричном случае n £ [-а, а], тогда уравне ния (19) имеют вид:

vt + vt +

r

r

-

-

CT2 ⁰ cosh (2at)^ v y

^CT2 ² cosh (2at^ v y

+ ^СТ 0 cosh ^(2at) v yy

+ ^CT 2 cosh(2at) v yy

+ ^CT2 0 ^{sinh (2at) | v} yy - CT ⁰ sinh (2at) Iv yy

- v y ¹ = rv, - v y I = rv.

Итак, для первой модели верхняя цена V = v (0, 0) и нижняя цена V = v (0, 0).

Во второй модели da t = ntatdt, то есть a t = a ₀ exp

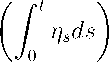
, неопределенный

параметр n t G [n t , n t ], a o - начальное условие. Уравнения (19) имеют вид:

x vt + rvy + ^(vyy x vt + rvy + у (vyy

- v y ) + A t xv' x + B t x | v x | = rv, - v y ) + A t xv' x - B t x | v X | = rv,

A t ⁼

n t ⁺ n t ,B t = n t ^- n t

с краевыми условиями v (T, y,x) = v (T, y,x) = f (y). Уравнения (21) являются двумерными уравнениями G-теплопроводности с x2

G i ⁽ x, t, v y , v x , v yy ) = rv y ⁺ у ^u "y ^- v y )⁺ A t xv 'x ⁺ B t x ^{| v} X \ ,

x ²

G 2 ^{( x}, t, v y , v x , v y ’ y ) = rv y ⁺ у cv y; — v y )⁺ A t xv x — B t x \ v x \ .

В симметричном случае, когда n t G [ — a t , a t ], уравнения (21) имеют вид:

x vt + rvy + ^Cvyy x vt + rvy + у (vyy

- v y ) + a t x\v' x\ = rv, — v y ) - a t x \ v X \ = rv.

4. Аппроксимация моделей с неопределенной волатильностью при помощи дерева

T

Произведем разбиение интервала [0,T] на N частей с шагом h = n . Рассмотрим

-

последовательность 5: 5 _n G {- 1,1 } , p _n = P (5 _n = 1) = ^ +

σ n ²- 1   ^√ _h

2 / фильтра-

^2a n - 1

цию F _n = a (5 1 ,..., 5 _n ) и последовательность AY _n = a _{n - 1} 5 _n Vh,Y o = 0, n = 1,...,N. Последовательность Aa n = a _{n - 1} n n h,n n A n n A n n . Рассмотрим следующие (стандартные) задачи стохастического оптимального управления в дискретном времени:

sup Ef(Y n) , η 1 ,...,η N -1

inf Ef (К n) .

η 1 ,...,η N -1

Введем функции: v ^N (n, y, x) =

(1 + rh) ^N

-

v (n,^y,x)= (1₊ rh) N -

- sup E (f (Y N )/Y n = y,a n -i = x), η n ,...,η _{N - 1}

- inf    E (f (Y n )/Y n = y,a n —i = x).

n η n ,...,η N-1

Таблица 3

Интервал справедливых цен в первой модели стохастической волатильности

Метод	Нижняя цена	Справедливая цена	Верхняя цена
Решение краевой задачи	0,4593	0,4755	0,5016
Рекуррентные формулы	0,4523	0,4767	0,5030

Справедливы следующие формулы:

vN(N, Yn, aN-i) = vN(N, Yn, aN-i) = f (Yn), vN (n — 1, y, x) =

——- sup E(v ^N (n, y + AY n , x + Aa n - 1 )/Y n - i = y, a n - 2 = x) =

• ¹    + ^rh П п - 1

= ——7 sup(pv ^N (n,y + x(1 + n n - i h)Vh, x(1 + n n - i h)) +

• ¹    + r^h П п - 1

  
  

+ (1 — p)v ^N (n, y — x(1 + n n - i h) Vh, x(1 + n n - i h))), v ^N (n — 1, y, x) =

——- inf E(v ^N (n,y + AY n ,x + Aa n - i )/Y n - i = y, a n - 2 = x) =

1 + rh n n-1

= ——7 inf (pv ^N (n, y + x(1 + n n - i h) Vh, x(1 + n n - i h)) +

• 1    + rh n n-1

+ (1 — p)v ^N (n, y — x(1 + n n - i h) Vh, x(1 + n n - i h))).

Справедливо следующее утверждение.

Утверждение 1. Если функция f (y) непрерывна и ограничена, то v (0, 0, ао) = lim vN (0,0, ао), N→∞ v (0, 0, ао) = lim vN (0, 0, ао) • N→∞

Отметим, что n i £ [n^nJA = !,•••,N; V (t,y,x) , v (t,y,x) — вязкостные решения уравнений (21) с краевыми условиями: V (T, y, x) = v (T, y, x) = f (y).

Доказательство утверждения является стандартным, см., например, [18, 19].

Пример 3. Пусть r = 0, 1, a = 0, 05, S ₀ = 5, K = 5, T = 1, N = 20. В табл. 3 приведены значения верхней и нижней цены европейского опциона с платежным обязательством f (Y T ) = max(S ₀ exp(Y T ) — K, 0), рассчитанные с помощью формул (20) и (24) в случае n £ [ — 1,1]. Случай n = 0 (a t = а ₀ ) соответствует ситуации, когда рынок полный, и справедливая цена вычисляется с помощью решения краевой задачи (3) (либо с помощью рекуррентных формул (6)), когда a = а о .

На рис. 3 приведены графики зависимости значений U (0,y), v (0,y), V (0,y) от y при K = 5. Сплошной линией нарисован график зависимости значений v (0,y) от у . Пунктирной линией нарисован график зависимости значений U (0,y) от у . Точечной линией нарисован график зависимости значений v (0,y) от у.

Пример 4. Пусть r = 0,1, а ₀ = 0,1, S ₀ = 5, K = 5, T = 1, a t = t. В табл. 4 приведены значения верхней и нижней цены европейского опциона с платежным обязательством f (Y T ) = max(S ₀ exp(Y T ) — K, 0), рассчитанные с помощью формул (22) и (24) в случае n t £ [ - a t , a t ]. Случай n t = 0 (a t = a ₀ ) соответствует ситуации, когда рынок

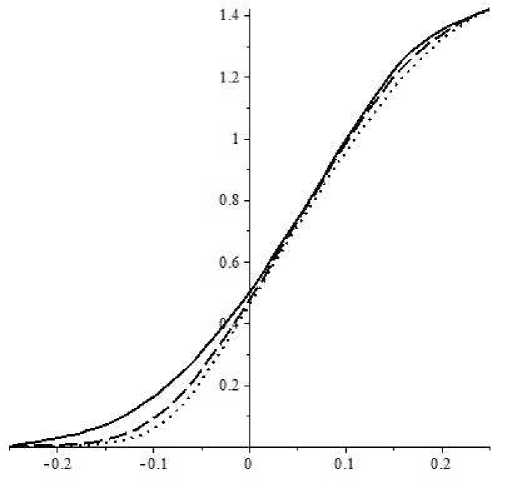
Рис. 3. Графики зависимости значений U (0, y ), v (0, y), v (0, у ) от у в первой модели неопределенной волатильности

Таблица 4

Интервал справедливых цен во второй модели стохастической волатильности

Метод Нижняя цена Справедливая цена Верхняя цена Решение краевой задачи 0,4312 0,5086 0,5403 Рекуррентные формулы 0,4360 0,5005 0,5405 полный, и справедливая цена вычисляется с помощью решения краевой задачи (3) с (либо с помощью рекуррентных формул (6)), когда ст = ст0.

На рис. 4 приведены графики зависимости значений U (0, у), v (0, у, ст о ,), v (0, у, ст о ) от у при K = 5. Сплошной линией нарисован график зависимости значений v (0, у, ст о ) от у . Пунктирной линией нарисован график зависимости значений U (0, у) от у . Точечной линией нарисован график зависимости значений v (0, у, ст ₀ ) от y.

Заключение

В статье продемонстрированы вычислительные методы, использующие разные техники, в моделях, в которых волатильность является одной из возможных траекторий, а именно, в модели Хестона со случайными траекториями, и в модели с неопределенной волатильностью, с детерминированными траекториями из доверительного множества возможных траекторий. Причем основное внимание уделено расчетам интервалов справедливых цен для второй модели. Первый метод основан на решении вязкостных уравнений с использованием разностных схем. Вторым является метод Монте-Карло, который основан на моделировании исходного процесса стоимости акции. Третьим является метод деревьев, который основан на аппроксимации исходной непрерывной модели дискретной моделью и получением рекуррентных формул на бинарном дереве для расчета верхней и нижней цен. Показано, что интервалы справедливых цен, полученные с использованием трех численных методов, практически

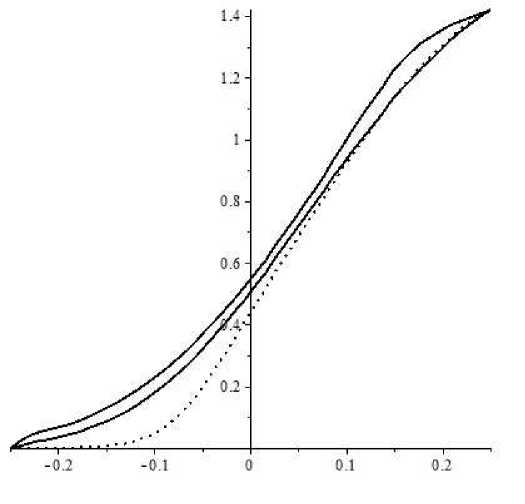
Рис. 4. Графики зависимости значений U (0, у), v (0, y, oq) , v (0, у, ^о) от у во второй модели неопределенной волатильности совпадают. Основной же вывод заключается в том, что модель с неопределенной волатильностью является адекватной заменой модели Хестона в случаях, когда необходимо вычислить интервал справедливых цен.