Модели управления гидротехническими проектами на пойменных территориях с учетом активности хозяйствующих субъектов

DOI:

Пойменные территории характеризуются повышенной зависимостью своего состояния от гидрологического режима, определяемого объемом весеннего паводка, русловой структурой и рельефом территории. Сложная структура русловой системы и зон затопления определяют мозаичность расположения функциональных зон пойменных территорий. В основе эффективности хозяйствования на пойменных территориях лежит принцип оптимальности соответствия территориального распределения водного ресурса функциональному распределению ее фрагментов. Именно поэтому поймы зарегулированных равнинных рек подвержены системной деградации вследствие техногенного нарушения их гидрологического режима фактом существования и режимом функционирования ГЭС.

Резкое нарушение природного динамического равновесия между вымыванием и осаждением донного грунта в главном речном русле ниже ГЭС запускает процесс медленного понижения (депрессии) речного дна на протяжении многих десятков километров [1; 3; 4; 7; 9; 15; 16]. Так, понижение уровней рек за годы работы ГЭС составляет: р. Камы у Воткинской ГЭС — 1,1 м, р. Волги у Нижегородской ГЭС — 1,3 м, р. Волги у Волжской ГЭС (ВГЭС) — 1,7–1,8 м [1; 3; 4; 9; 15; 16]. Это является причиной снижения объема паводковых вод, поступающих в поймы [5; 9; 15; 16]. Результатом этого снижения является прогрессирующее сужение устойчиво затапливаемой пойменной территории, являющейся биотопом ее природной системы, и расширение наименее ценной в социо-природохозяйственном отношении неустойчиво затапливаемой территории [2; 6; 13].

Среди пойм, в значительной степени сохранивших к настоящему времени свое природное значение, особое положение занимает Волго-Ахтубинская пойма (ВАП) — уникальное природное образование, протянувшееся почти на 450 км в полупустынной зоне юга России — последний, практически единственный участок долины р. Волги, сохранивший естественное строение. Создание каскада крупнейших гидроэнергетиче- ских узлов и водохранилищ на р. Волге и, особенно, ВГЭС стало главным фактором деградации ВАП [2; 6].

В последнее десятилетие активно обсуждаются проекты обводнения территории ВАП за счет прокладки каналов и возведения плотин в русле р. Ахтубы и малых руслах пойменной территории. Для увеличения объема финансирования (и, следовательно, результативности) таких проектов в их финансировании наряду с органом власти (Центром) должны участвовать экономические субъекты территории (агенты), получающие финансовую выгоду от их реализации. В этой связи актуальность приобретает задача поиска оптимальных алгоритмов смешанного финансирования проектов увеличения обводнения пойменных территорий и их реализация для территории ВАП. В известных моделях смешанного финансирования набора (портфеля) проектов [10] предполагается, что инициатива реализации каждого из отдельных проектов исходит от заинтересованного в нем агента, а Центр, исходя из своей целевой функции (аддитивной относительно отдельных проектов) и имеющегося ресурса, находит оптимальный для него портфель проектов и величины своего софинансирования каждого из вошедших в него проектов. Недостающее финансирование каждого проекта вносит соответствующий агент.

Целями рассматриваемого здесь гидротехнического проекта является увеличение площади паводкового затопления территорий, значимых для пойменной экосистемы в периоды маловодья (экологический эффект Центра) и сохранение воды в малых руслах территории в период межени для орошения сельскохозяйственных территорий (экономические эффекты агентов). Рассмотрим проект установки в руслах поймы комплекса плотин, увеличивающего поступление паводковых вод в некоторые русла с их выходом на целевую пойменную территорию за счет ограничения их поступления в другие русла. Назовем простым проектом (или просто проектом) установку плотины в основании некоторого русла, а мультипроектом — совокупность простых проектов. Особенностью пойменных территорий является сложная иерархически-сетевая структура ее малых русел. Поэтому целевая функция Центра этого проекта может быть в одних случаях аддитивной, а для других — неаддитивной относительно вкладов отдельных плотин в общий проектный эффект. Для такого мультипроекта агентов можно разделить на две группы: первую группу образуют агенты, заинтересованные в установке отдельной плотины, удерживающей воду в «их» русле в течение меженного периода (их целевая функция зависит только от «своего» проекта), агенты второй группы заинтересованы в дополнительном обводнении территории. Их целевая функция определяется мультипроектом в целом. Далее рассматривается только первая группа агентов. Без снижения общности будем считать, что каждый проект имеет заинтересованного в нем «своего» агента, а каждый агент заинтересован в реализации одного «своего» проекта.

1.    Постановка задач управления проектами

Задача оптимизации мультипроекта с учетом софинансирования агентов имеет вид:

n

Ф(х(У),v,q) ^ max, V^ - q i ) <  R,                   (1)

V i=1

F i = (T i f i - q i )v i ^ max, 0 <  q i <  T i f i , i = 1,...,n.                 (2)

Q i

Здесь Ф, R — соответственно целевая функция и проектный ресурс Центра; v =

= (v1,..,vn) — управление Центра (vi = 1 — i-й проект реализуется, vi = 0 — i-й проект не реализуется); ri — стоимость i-го гидротехнического проекта; V, x(V) — соответственно объем первой фазы весеннего паводка и его функция распределения; п, Fi, fi,Ti,qi — соответственно число агентов и проектов, целевая функция, ежегодный доход, субъективный горизонт планирования i-го агента, размер софинансирования проекта i-м агентом.

Соотношения (1), (2) задают семейство теоретико-игровых моделей управления, различающихся условиями информированности игроков и порядком их действий. Рассмотрим две наиболее простые модели.

В модели М 1 , реализуемой игрой Г 2 (Г 0 ) , Центр, которому известны все параметры задачи (1), (2), находит оптимальное решение задачи (1) — свою гарантирующую стратегию v ⁹ (x(V )) = v ⁹ (x(V)V) c софинансированием со стороны агентов V и добивается его реализации, играя с ними в игру Г 2 (Г о ) ( V — доминантные стратегии агентов в их игре Г о ). Заметим, что Центр в общем случае не может добиться максимального софинансирования q _t = T _i f _i — ^ (i = 1,...,п) в связи с положительной величиной резервной полезности части агентов при реализации Центром оптимального для него мультипроекта только за собственные средства (в условиях ресурсного ограничения ^П =1 r _t <  R ). Поощрительная надбавка ε, вводимая Центром для реализации гарантированного равновесия совокупности игр Г ₂ может компенсировать незначительную неопределенность его знания величин T _i f _i . Решением задачи (1), (2) в модели М 1 (при T _t = 1(i = 1, ...,п) ) является вектор:

V = f ^v9 , q i = q ^a i

(^v o , q i , ^{( i e} 1 ⁹ );

v ⁹ = argmax(Ф(x(V),V)), V(r — ql) <  R,

V                 ^—^

i e i e

n qi = fi(X(VVv9) — £ > 0,V0 = argтах(ф(хОЛ),v)), Vri < R.

V                             '

i =1

В (3) множество 1 ⁹ является подмножеством множества индексов i = 1,...,п , удовлетворяющих условиям: v ⁹ = 1,v ⁰ = 0 . Вектор V = (q ¹ ,...,q n ),q i = q ⁹ ,i e 1 ⁹ ; q i = 0,i e 1 ⁹ является равновесием в доминантных стратегиях игры Г _о агентов, которая разыгрывается ими после получения от Центра информации о векторе конфигурации мультипроекта v , являющимся его гарантирующей стратегией в игре Г ₂ . Зависимости f _i (x(V),v) вычисляются Центром при помощи гидродинамического моделирования на основе известных ему оценок зависимостей f _i (x(V )) или на основе сообщений агентов ^s (f _i (x(V ))) . Данный механизм при отсутствии неопределенности, очевидно, обладает наибольшей эффективностью.

В связи с неопределенностью величин Ti Центр в решении (3) вынужден использовать значения T _i = 1 (i = 1,..,п) , что потенциально снижает эффективность решения (3). Это ограничение снимается в модели М 2 , реализующей игру ( Г 1 (Г ₀ ) ) (Центр может использовать М 2 в условиях существенно неполной информированности или невозможности использования модели М 1 ). В этой модели Центр сообщает агентам значение проектного ресурса R и условие или решение задачи (1) v * (x(V),R) с параметром R . Вектор заявок агентов на софинансирование q ^N является равновесием Нэша их игры Г _о (2) (наихудшим для Центра случаем является q ^N = 0 ). Узнав это решение, Центр решает задачу Ф(x(V ),v,q ^N ) ^ max ^ , ^_{ie I a} (г — q ^N ) < R . Величины софинансирования агентов, чьи проекты не вошли в реализуемую версию мультипроекта, обнуляются.

Практическая реализация этой модели для задачи (1), (2) затруднена сложностью поиска агентами равновесия Нэша q ^N в однократно разыгрываемой игре Г 0 и его практической нереализуемостью при п >  3 . С целью облегчения этого поиска Центр может предложить им «решатель», реализующий численный алгоритм поиска q ^N (см. ниже алгоритмы 1 и 2). Для снижения неопределенности при реализации равновесий Нэша Центр может установить наиболее выгодный для него порядок действий (очередность объявления заявок) агентов.

Если проекты расположены в независимо затапливаемых фрагментах территории, то целевая функция Центра аддитивна по экологическим эффектам проектов и задача (1) принимает вид:

п                п

V V i ^ i ^ max, У2(^г ^ - ^М <  R, ^v i £ {0; 1},

V i=1                 i=1

где ф _г — эффекты Центра от каждого проекта.

2.    Алгоритмы решения задачи (2), (4) в модели М2

При решении задачи (2), (4) в рамках модели М 2 Центр, зная вектор софинанси-рования q ^N , решает задачу целочисленного программирования (4) (задачу о рюкзаке) методом динамического программирования. При небольшом числе агентов (и проектов) для заданного R при поиске q ^N возможно рассмотрение каждым агентом всех потенциально реализуемых вариантов мультипроекта. Каждый агент определяет перечень выгодных ему вариантов мультипроекта, а также диапазоны софинансирования, которые позволят ему обеспечить реализацию каждого из них.

Приведем алгоритм поиска оптимальных стратегий софинансирования агентов в задаче (2), (4) в рамках модели М 2 на примере 1 для 3-х агентов и проектов. Числовые данные примера 1 приведены в таблице 1.

Таблица 1

Пример 1. R=2, n=3

Проект	№1	№2	№3
r i	1	2	3
Ф i	4	5	6
T i f i	1/2	3/2	7/4

С учетом данных таблицы 1 потенциально реализуемыми является следующие варианты мультипроекта: {1} , {2} , {3} , {1;2} , {1;3} , {2;3} . Соответствующие диапазоны софинансирования агентов приведены в таблице 2.

Для поиска равновесия используем концепцию угроз-контругроз [8]. Угрозой игроку будем считать мультипроект, не содержащий проект игрока. Ответом игрока на угрозу будем считать более ценный для Центра мультипроект, содержащий проект иг- рока.

Таблица 2

Пример 1. Диапазоны софинансирования агентов

Набор проектов	9 1	9 2	9 3
{ 2;3 }	-	[5 / 4;6 / 4]	[6 / 4;7 / 4]
{ 1;3 }	[1 / 4; 1 / 2]	-	[6 / 4;7 / 4]
{ 1;2 }	[0;1 / 2]	[1 / 2; 1]	-
{ 3 }	-	-	1
{ 2 }	-	0	-
{ 1 }	0	-	-

Из таблицы 2 можно видеть, что агент 3 имеет угрозу в виде варианта мультипроекта {1;2} . Ответами на нее являются варианты {2;3} и {1;3} , поэтому агент 3 полагает q ₃ = 7/4 . Если при этом q ₂ = 5/4 , то реализуется вариант {2;3} . Уменьшение софинансирования для агента 2 возможно при реализации варианта {1;2} . В таком случае агенту 2 угрожает вариант {1;3} , поэтому ему необходимо создать условия, при которых агент 1 заплатил бы меньше, чем для варианта {1;3} . Полагая, что агент 1 платит 1/4 — 5, агент 2 платит 3/4 + 5. В итоге, вектор софинансирования имеет вид q ^N = (1/4 — 5 ; 3/4 + 5 ; *) , где 5 G (0; 1/4] . Символом ( * ) отмечено предложение агента, проект которого не реализуется. Величины предложений агентов, чьи проекты заведомо не входят в мультипроект, для определенности предполагаются максимальными.

Полученный вектор софинансирования с параметром δ представляет семейство равновесий Нэша. Добиться единственности равновесия Нэша можно при введении Центром порядка принятия решения агентами. В рассматриваемой задаче, если агент 2 принимает решение раньше, чем агент 1, то вектор софинансирования принимает вид q ^N = (1/4 — е ;3 / 4 + е ; *) (здесь е - произвольно малая величина). Если первым принимает решение агент 1, то ^ = (0; 1; *) .

На рисунке 1 представлены параметрические зависимости целевых функций Центра для решения задачи (2), (4) примера 1 в рамках моделей М 1 и М 2 с параметром R . Нижняя пунктирная линия соответствует решению задачи (4) без софинансирования агентов, а сплошная линия - решению задачи примера 1 в рамках модели М 1 при е = 0 . Средняя пунктирная линия отвечает решению задачи (2), (4) в рамках модели М 2 .

Для большого числа агентов реализация описанного выше алгоритма поиска решений задачи (2), (4) практически невозможна. Рассмотрим алгоритмы поиска решений задачи (2), (4), не зависящие от числа игроков, но использующие идею «угроз» и «контругроз».

Алгоритм №1

Варианты мультипроекта упорядочиваются по убыванию целевой функции Центра (экологической ценности): Ф 1 > Ф ₂ > ... > Ф _{т -1} > Ф _т ( т = 2 ^п — число вариантов, Ф _г — экологическая ценность г -го варианта).

Для всякой угрозы игроку j подбираются все его возможные ответы. Ответ на угрозу реализуется автоматически (игрок j платит 0), если платы других игроков хватает для реализации данного варианта мультипроекта. Иначе игрок j вносит недостающую часть стоимости варианта.

Перенумеруем варианты в соответствии с понятиями «угроз» и «ответов на угрозы»: Ф 1 1 > Ф 1 ₂ > ... > Ф 1 _т1 > Ф 1 > Ф 2 1 > ... > Ф 2 _т2 > Ф 2 ... , где Ф * — i -ая угроза игроку j , Ф^ — k -ый ответ на i -ую угрозу, m i — число ответов на i -ую угрозу. Отметим, что если вариант является ответом на угрозу г , то он является и ответом на угрозы г + 1 , г + 2 и т.д. Таким образом, множество ответов на каждую следующую угрозу будет включать и множество ответов на предыдущую угрозу. Введем обозначения: ответ на 1-ю угрозу — 1 1 , I 2 ,..., 1 _{m i} , на 2-ю — 1 1 , I 2 ,..., 1 m i ,2 1 , 2 2 ,..., 2_W , на 3-ю — 1 1 , 1 2 ,..., 1 m i , 2 1 , 2 2 ,..., 2 _т 2 ,3 1 , 3 2 ,..., 3 _т з и т.д.

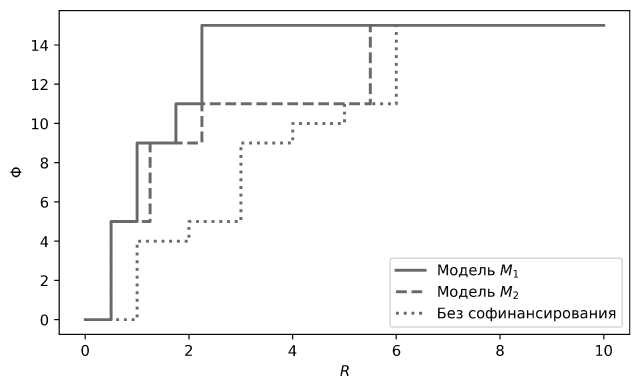
Рис. 1. Целевая функция Центра для решения задачи (2), (4) примера 1 в моделях М 1 и М 2

Очевидно, что игрок j из всех ответов на каждую угрозу выбирает тот, который требует меньшей платы. Так как все угрозы возможны для реализации, то выбирается максимальная плата по всем возможным угрозам. Вследствие ограниченности платы, игрок j выбирает минимум из максимально возможной платы и платы, гарантирующей предотвращение всех угроз. Таким образом, q? = min(7} fj, max(min(q1i,..., q1mi), min^i,..., q1mi ,q2i,..., q2m2),...)), где qik = max(Q,pj + ^(pi — q?) — Я), I — номера проектов за исключением j, входящих в вариант i^. Методом математической индукции (по количеству угроз t) доказано равенство:

^max(min(q 1 i ,...,q 1 _mi ), ^min(q 1 i , ...,q 1 _mi ,q 2 i ,..., q 2 _m2 ),...) = ^min(q 1 i ,..., q 1 _mi ).

Краткое описание алгоритма 1:

• 1)    Выбираем такие варианты мультипроекта, для которых X_l P _l < ^ + X_l ^ l f _l , где I — номер проекта в варианте. То есть выбираются потенциально реализуемые варианты.

• 2)    Полученные в п.1 варианты упорядочиваются по убыванию величины целевой

функции Центра (экологической ценности).

• 3)    Для каждого агента j :

• •    ищется первая угроза — вариант без участия «его» проекта;

• •    все варианты, экологическая ценность которых больше угрозы, считаются ответами на эту угрозу;

• •    агент выбирает, какой из ответов софинансировать, исходя из гипотезы рациональности: q N = min(g 1 1 , ...,q _1mi ) , где m 1 - число ответов на угрозу, q^ = max(G,p _J + £_;. рц — R — ^ц q N ) ( l _i — номера проектов, кроме j , входящих в ответ i на угрозу для агента j );

• •    в случае, если агент не имеет средств для минимального софинансирования, он вкладывает все средства: q N = min(T j f j , min(q 1 1 ,...,q _{1 mi} )) .

• 4)    Для поиска равновесия Нэша решается си стема уравнений:

q N = min(T j f j , min(q 1 1 , ...,4 1 )) , Vj G 1,n , где n — число агентов.

В результате решения задачи (2), (4) в примере 1 для R = 2 алгоритмом №1 найдено равновесие Нэша q ^N = (G.5; 1.5; 1.5) , реализующее вариант мультипроекта {2;3} с доходом Центра, равным 11, что больше дохода, получаемого им в ранее найденном решении. Этот факт послужил мотивом разработки алгоритма №2 с более узким множеством актуальных угроз, что потенциально ведет к расширению множества решений.

Алгоритм №2

В алгоритме №1 рассматриваются все потенциально реализуемые варианты мультипроекта, то есть такие, что £_; p i <  R + ^2_iT _i f _l , где l — номер проекта в мультипроекте. При этом для каждого игрока рассматривалась угроза с наибольшим экологическим эффектом. Однако создавались ситуации, в которых данная угроза не реализовывалась, но агенты опирались на нее в принятии своих решений. В данном алгоритме предлагается ориентироваться непосредственно на текущую ситуацию и на текущую угрозу.

Краткое описание алгоритма №2:

• 1)    В начале работы алгоритма по-прежнему выделяются все потенциально реализуемые мультипроекты.

• 2)    Среди них выделяется угроза, актуальная на данный момент (то есть та, которая существует даже при нулевом векторе софинансирования), и вычисляется доход, получаемый Центром при ее реализации.

• 3)    Каждый агент пытается определить, необходимо ли ему изменять свое софинан-сирования для изменения текущей ситуации:

• •    агент, чей проект входит в угрозу, не заинтересован в изменении своего со-финансирования;

• •    агент, чей проект не входит в угрозу, пытается найти ответы на нее. Для этого среди всех потенциально реализуемых вариантов мультипроекта ищутся те, чей эффект для Центра больше того, который соответствует текущей угрозе, и в состав которых входит проект рассматриваемого агента. Среди всех альтернатив агент ищет такой мультипроект, который обеспечивает ему минимальное софинансирование.

  
  

После всех ходов агентов производится обновление текущей угрозы и соответствующего ей дохода Центр.

• 5)    Алгоритм заканчивает работу, когда вектор софинансирования перестает изменяться.

Данный алгоритм можно использовать в модели, учитывающей порядок действий игроков. Для этого достаточно обновлять вектор софинансирования после хода каждого агента. Рассмотрим пример 2 задачи (2), (4) для модели М 2 .

Таблица 3

Пример 2. R=30, n=5

Проект	№1	№2	№3	№4	№5
Г г	12	18	19	15	16
ф i	31	25	35	20	36
T i f i	2,6	2,6	3,7	4,7	4,4

Результаты решения примера 2 задачи (2), (4) для модели М 2 алгоритмом №2 приведены в таблице 4.

Таблица 4

Оптимальные стратегии агентов в примере 2 задачи (2), (4) для модели М 2

R	Вектор софинансирвоания агентов	Реализуемый набор проектов
15	( * ; * ; * ; * ; 1)	{ 5 }
30	(0; * ; * ; * ; 0)	{ 1;5 }
45	(0; * ;2; * ;0)	{ 1;3;5 }
60	(0; * ; 1; 1; 0)	{ 1;3;4;5 }
75	(0;0;0; * ;0)	{ 1;2;3;5 }

На рисунке 2 изображены параметрические зависимости целевых функций Центра от ресурса R для ситуации без софинансирования и для моделей М 1 и М 2 в примере 2.

3.    Эвристический алгоритм решения задачи (1)

Решение задачи (2), (4) происходит в два этапа: на первом этапе центр решает задачу (1) с параметром R Е [0; R ^max]. Результатом ее решения является параметрическая зависимость «затраты-выход» Ф^^^ ), R)) . На втором этапе Центр решает задачу софинансирования мультипроекта, используя модели М 1 или М 2 .

В случае неаддитивной целевой функции задача (1) имеет экспоненциальную сложность. Однако, наличие неустранимой погрешности е^ численного построения карт за- топлений пойменной территории позволяет ограничиться поиском квазиоптимальных решений задачи (1) эвристическими алгоритмами. С учетом этого соображения для поиска оптимальных конфигураций плотин в малых руслах поймы построен эвристический ал- горитм «доноры-акцепторы» (ДА-алгоритм). Алгоритм находит оптимальную конфигурацию плотин для фиксированного гидрографа Q(t), поэтому на предварительном этапе на основе функции x(V) и пределов объема гидрографа малых паводков определяется базовый постоянный гидрограф Gme = (Qme,tme), параметры Qme,tme которого являются средними значениями параметров маловодных гидрографов. Русловая система поймы, насчитывающая М малых русел, разделяется на «доноров», «трансакцепторов» и «акцепторов». «Акцепторы» — это целевые русла, в микрозонах которых сконцентрировано большое количество целевых экологических ячеек (то есть ячеек, не затопленных на карте К(Gme), но затопление которых увеличивает значение Ф) цифровой карты территории. Микрозоной каждого русла в данном алгоритме считается часть территории, каждая точка которой удалена от русла не более, чем на расстояние S/L, где S — площадь целевой зоны, L — совокупная протяженность ее малых русел. В класс «трансакцепторов» входят русла, из которых вода может попадать в «акцепторы» согласно направлению течений. «Доноры» определяются, исходя из заданной группы акцепторов, и являются объектами для потенциальной установки плотин. В число «доноров» входят русла, не являющиеся ни «акцепторами», ни «трансакцепторами», и при этом являющиеся их ответвлениями согласно ориентированному графу русел. Таким образом, объем вод из «доноров» может быть передан по течению «акцепторам» путем установки в их основаниях переливных плотин, высота которых обеспечивает их полное заполнение без выхода вод на территорию.

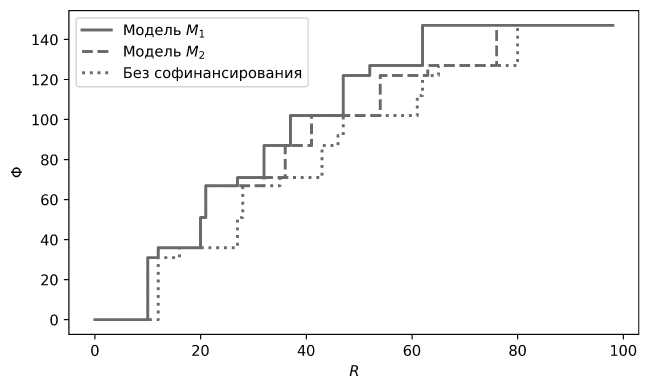
Рис. 2. Целевая функция Центра для решения задачи (2), (4) примера 2 в моделях М 1 и М 2

Входными данными ДА-алгоритма являются: максимальное число плотин в малых руслах п = 1,..,М , карта К(G ^me ) затопления территории, граф русел пойменной территории Gr(N,E ) ( N — множество русел, Е — множество связей между ними). Ранжирование «акцепторов» производится на основе оценки площади целевой территории в их микрозонах. Подбор множества «акцепторов» осуществляется взятием первых s(s Е { 1,...,М }) русел из списка всех русел, упорядоченного по числу целевых ячеек в их микрозонах.

На предварительном этапе для каждого русла с Е N вычисляются значение его рейтинга Rc (количество целевых ячеек в его микрозоне) и оценка суммарного объема V, который потенциально может быть предоставлен данным руслом при его перекры- тии, равного поступающему в него объему вод за вычетом объема, необходимого для его максимального заполнения. В результате составляется Rating — список русел, упорядоченных в порядке убывания значений Rc.

На основном этапе для каждого значения s строятся множество «акцепторов» A _s как первые s русел из списка Rating , множества «трансакцепторов» TS_s и потенциальных «доноров» PD _S при помощи поиска в ширину по графу Gr(N,E ) с инвертированными дугами, начиная от каждой вершины из A _s ; множество актуальных «доноров» D _s и соответствующий ему вектор конфигурации 5 _S = ( 5 _{1 s} ,..., 5 _Ms ) , b _j8 e{ 0;1 } ,j = 1,..,М получается путем решения следующей задачи о рюкзаке: ^2_cePD b _cs V _c ^ max , n _s = = C lDced_C ^ _C s < n , а также рассчитываются верхние оценки количества дополнительно затопленных ячеек Л ₅ и приращения ЛФ ₅ целевой функции по формулам: Л ₅ = = mm(TT _s ,TV^h^mm) - 1 ) , ЛФ ₅ = Л _В Л , Л = max_w Л^, TT _S = Z_cEA_a R c , TV _S = Z_cd ^ C , где h ^min — минимальная высота затопления, гарантирующая факт «затопления» ячейки цифровой карты, A _{i m} — коэффициент экологической ценности фрагмента пойменной территории.

После этого решается задача:

ЛФД5ДК(G ^me ),п)) ^ max.

S

Решение задачи (5) — оптимальное число «акцепторов» s * (n) , вектор оптималь-

-*

-*

ной конфигурации плотин 5 * (К(G ^me ),n) = 5 _S * (К(G^me),n) с числом плотин n _s * (п) и величина ЛФ( 5 * (К (G ^me ),n)) , отвечающие исходной карте затопления К(G ^me ) — считаются результатом работы ДА-алгоритма. Максимальное оптимальное число плотин равно п ^тах = max _s * ( _n ) n _s * , 1 <  п <  М .

Описанный эвристический алгоритм находит приближенное решение оптимизационной задачи с погрешностью максимизации целевой функции, но с точным учетом ограничения по проектному ресурсу, благодаря решению задачи выбора доноров из множества потенциальных доноров методом динамического программирования.

4.    Результаты решения задачи (1) для территории Волго-Ахтубинской поймы

Расчет целевой функции Центра при решении задачи (1) для территории северной части ВАП ДА-алгоритмом проводился по цифровым картам паводковых затоплений, построенных в ходе численного моделирования динамики поверхностных вод с использованием программного комплекса EcoGIS-Simulation [11; 12; 14]. В качестве базового использовался гидрограф с параметрами Qme = 21000м3/с, tme = 10 суток. Для расчета экологического эффекта использовалась цифровая карта ВАП с отмеченными ячей- ками территории, затопление которых необходимо для повышения величины площади стабильно затапливаемой экологически значимой территории. Связь ДА-алгоритма с цифровой моделью рельефа осуществлялась с помощью разработанного программного приложения «Редактор русел». Значение целевой функции Центра в результате реализации найденных ДА-алгоритмом решений задачи (1) рассчитывалось по цифровой карте затоплений территории с рельефом, имитирующим установку плотин в руслах-донорах. В проведенных вычислительных экспериментах среднее значение относительной разности объема водных ресурсов, переданных от русел-доноров в русла-акцепторы ВАП, при прямом гидродинамическом моделировании и оценки этого объема в решениях зада- чи (1), найденных ДА-алгоритмом, составила 8 %.

На рисунке 3 приведена рассчитанная ДА-алгоритмом зависимость размера группы доноров от размеров группы акцепторов. На рисунке 4 приведена зависимость оценки предоставленного донорами суммарного объема воды от размеров группы акцепторов.

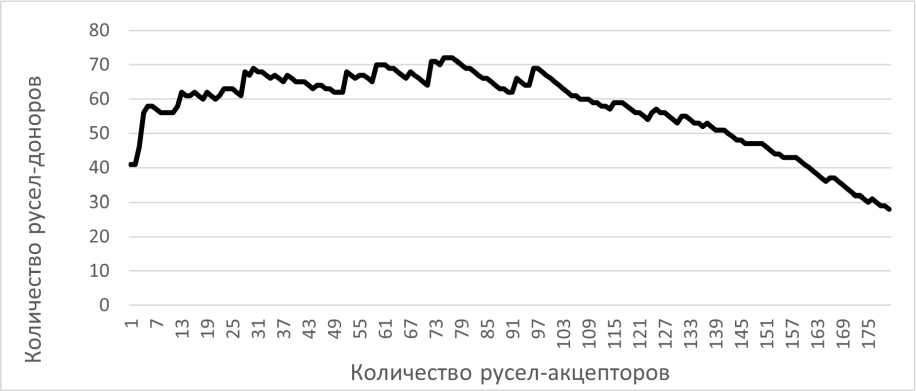
Рис. 3. Зависимость числа оптимального русел-доноров от числа русел-акцепторов ВАП

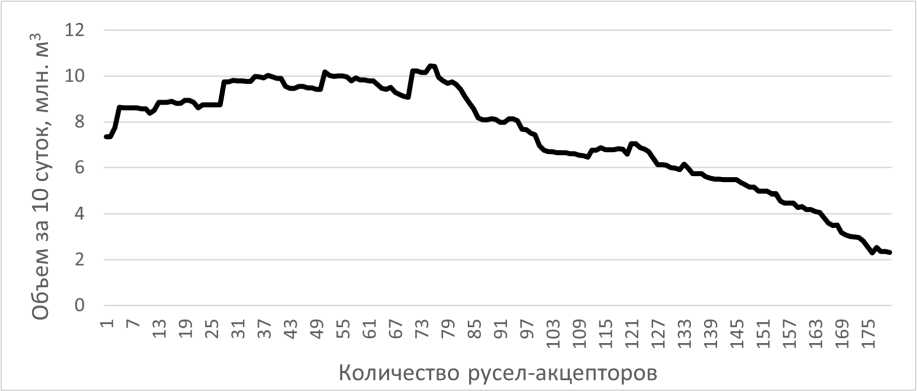
Рис. 4. Зависимость оценки дополнительного объема воды, попадающего в русла-акцепторы ВАП, от количества акцепторов

На рисунке 5 приведена карта ВАП, на которой отмечены русла-акцепторы и русла-доноры для одного из решений задачи (1) для территории ВАП. Для этого решения увеличение числа затопленных экологических ячеек составило 31 %. На рисунке 6 приведена зависимость проектного эффекта Центра от числа плотин в малых руслах ВАП. Вертикальная черта иллюстрирует условную величину проектного ресурса Центра, а длины горизонтальных стрелок — условные величины софинансирования со стороны агентов, необходимого для реализации соответствующих проектов.

Заключение

В настоящей статье проведено исследование проблемы управления гидротехническими мультипроектами установки системы паводковых плотин на пойменных территориях с учетом активности ее хозяйствующих субъектов. Различие в величинах экологического и экономического эффекта для разных вариантов мультипроекта позволило исследовать задачу синтеза оптимального механизма его софинансирования. Для исследования данной проблемы построены и исследованы математические модели иерархических игр Г2(Г0) и Г1(Г0). Для численного поиска равновесий Нэша в играх агентов Г0 предложено два алгоритма, использующие метод «угроз-контругроз». Работа алгоритмов проиллюстрирована на модельных примерах. В случае аддитивности мульти-проектного эффекта по эффектам составляющих его простых проектов установки одной плотины для поиска гарантированного решения игр Центр решает задачу целочисленного программирования, в случае неаддитивности – использует какой-либо эвристический алгоритм. Последний случай реализован при исследовании мультипроекта для территории северной части Волго-Ахтубинской поймы. Параметрическая зависимость «затраты-эффект» для этого мультипроекта найдена специально разработанным эвристическим алгоритмом «доноры-акцепторы». Расчет целевой функции Центра проводился по цифровым картам паводковых затоплений, построенных в ходе численного моделирования динамики поверхностных вод с использованием программного комплекса EcoGIS-Simulation. Связь алгоритма «доноры-акцепторы» с цифровой моделью рельефа осуществлялась с помощью разработанного программного приложения «Редактор русел». Значение целевой функции Центра в результате реализации найденных ДА-алгоритмом решений задачи (1) рассчитывалось по цифровой карте затоплений территории с рельефом, имитирующим установку плотин в руслах-донорах.

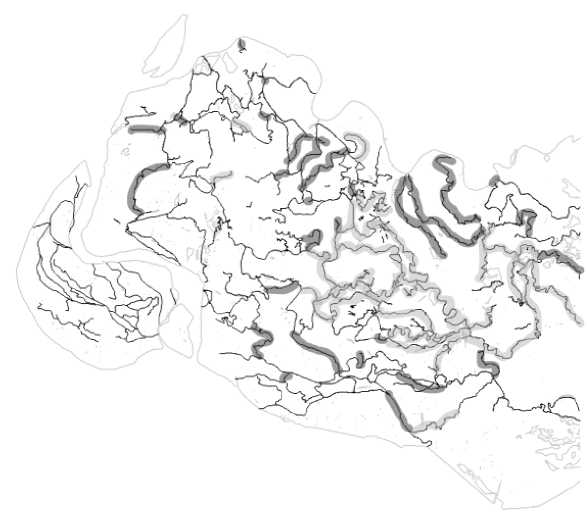
Рис. 5. Русла-акцепторы (отмечены светло-серым) и русла-доноры (отмечены темно-серым)

ВАП для одного из решений задачи (1) при Q = 21 000 м ³ / с, t = 10 суток

В целом проведенное исследование показывает потенциальную практическую при- менимость предложенной модели управления гидротехническими проектами с учетом участия хозяйствующих субъектов и разработанных алгоритмов для реализации гидро- технических проектов на пойменных территориях.

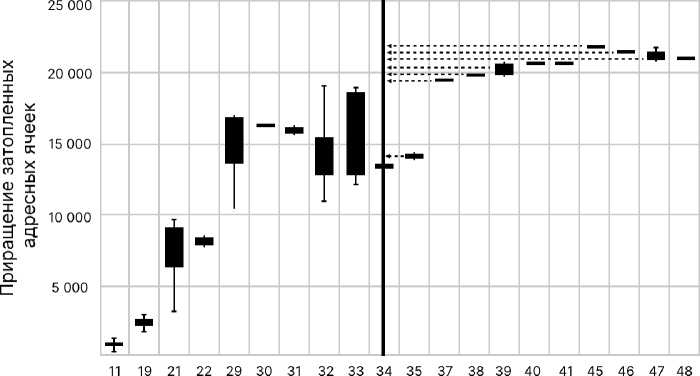
Количество дамб

Рис. 6. Зависимость проектного эффекта Центра от числа плотин в малых руслах ВАП

С другой стороны, как показали результаты проведенного исследования, использование плотин в малых руслах ВАП для увеличения площади устойчиво затапливаемой территории является малоэффективным. Для достижения этой цели более перспективным представляется использование паводковых плотин с изменяющимся поперечным сечением на р. Волге или на р. Ахтубе. В этом случае вариантами проекта являются места расположения этих плотин и, соответственно, места дополнительного устойчивого затопления. Исследование математической модели управления таким проектом в системе с активными агентами, относящейся к классу коалиционных игр, является предметом будущих исследований.