Модели, задачи и алгоритмы ситуационно-адаптивного планирования радиоресурсов систем мобильной широкополосной связи
Автор: Султанов Альберт Ханович, Камалов Артур Эрнстович, Кузнецов Игорь Васильевич
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 1 т.9, 2011 года.
Бесплатный доступ
Дается краткий обзор моделей, задач и алгоритмов ситуационно-адаптивного планирования канальных ресурсов в системах мобильной широкополосной связи. Методология ситуационно-адаптивного планирования является развитием методов принятия технических решений по повышению эффективности использования радиоресурсов за счет их наилучшего распределения в зоне обслуживания. Она позволяет учесть изменение нагрузки на уровне всей сети, неопределенность позиционирования мобильных станций и «мультисервисность» трафика.
Ситуационно-адаптивное планирование, узел спроса, скрытая марковская модель, алгоритм витерби, алгоритм баума-уэлша
Короткий адрес: https://sciup.org/140191445
IDR: 140191445 | УДК: 621.39
Текст научной статьи Модели, задачи и алгоритмы ситуационно-адаптивного планирования радиоресурсов систем мобильной широкополосной связи
Одним из направлений достижения максимального потенциала по предоставлению населению услуг широкополосной связи может стать эффективное использование ресурсов систем мо- бильной радиосвязи. Это означает распределение или перераспределение ресурсов (канальных, частотных, временных, энергетических и т.п.) ограниченного объема с учетом локально-территориального и временного изменения трафика в зоне обслуживания на основе решения оптимизационных задач планирования. Предлагаемая методология ситуационно-адаптивного планирования радиоресурсов включает комплекс задач, начиная от разработки модели изменения нагрузки в сети и уточнения ее параметров и заканчивая алгоритмами непосредственного управления этими ресурсами, базирующимися на оптимизационных методах. Эту методологию можно рассматривать как дальнейшее развитие методов принятия технических решений по повышению эффективности использования радиоресурсов в системах мобильной радиосвязи. В отличие от известных [1], она учитывает территориальное изменение нагрузки во всей системе (не только на уровне отдельных сот), неопределенность позиционирования мобильных станций в зоне обслуживания и «мультисервисность» трафика, что особо важно для широкополосных систем мобильной радиосвязи.
Модель ситуационно-адаптивного планирования
В основе моделирования лежат следующие допущения.
-
1. Обслуживаемая системой мобильной связи территория разбивается на ряд локальных участков – узлов спроса. Узел спроса рассматривается как источник сообщения телеграфного сигнала.
-
2. Процессы в системе удовлетворяют условиям марковости.
-
3. Поток заявок (звонков) осуществляется в условиях неопределенности позиционирования мобильных станций.
-
4. Узлы спроса могут обслуживаться несколькими смежными базовыми станциями (БС).
-
5. Вид запрашиваемой услуги идентифицируется достоверно.
В качестве математической модели описания берется система массового обслуживания, описываемая в виде скрытых марковских последовательностей – моделей (СММ) [2].
Определим ‘ад-л как состояния модели (выделенные узлы спроса), s = № 5W} – / = 1Л множество состояний модели (N – число узлов спроса). Пусть в дискретный момент /. времени «звонок» поступает из любого (произвольного) узла спроса S’. Ввиду того, что состояние ^ к в наблюдаемый момент времени в общем случае может быть неизвестно, введем переменную qt. Переменную q, будем интерпретировать как заявку из некоторого узла спроса sв момент времени tj . Должно быть известным распределение вероятностей выбора начального состояния л = клд, то есть ^ = P^ = S?) (вероятность того, что в начальный момент t — tx будет поступать звонок из узла St), и известна условная вероятность перехода ak! из состояния sв состояние s! 9 то есть аи =p
Обозначим ^ — {aA7 } матрицу переходных вероятностей размерности NxN . Введем в рассмотрение множество предоставляемых услуг p = ^ ... vM}, где параметр Vm обозначает m -ую услугу, которая может быть «привязана» к адресу (номеру) входящего «звонка»; М – число предоставляемых услуг. Множество V в СММ еще называют множеством наблюдаемых объектов.
Пусть в процессе наблюдения за обслуживаемой территорией в течение некоторого времени имеет место последовательность входящих «звонков» O = {o,...or}, где on – некоторый объект (то есть on – входящий звонок услуги V , «привязанный» к узлу спроса qt ); T – длина наблюдаемой последовательности объектов. Будем считать известной условную вероятность 1^1) = P(o, =vm\ql=Sl) того, что в состоянии si наблюдался звонок абонента с заявкой на vm услугу. Условная вероятность b^m) должна удо влетворять условиям: b,^m)>0, l = \,N, m = l,M, м __
-
и "^biOn) = 1, 1 = \,N.
Совокупность всех условных вероятностей b^m^ образует матрицу B вероятностей появления m-го объекта при реализации l -го состояния размерности .
Будем считать, что в общем нестационарном поведении трафика можно выделить ряд «элементарных» стационарных ситуаций, например, резкое увеличение (снижение) концентрации людей на улицах в начале и конце рабочего дня, периодические всплески на остановках общественного транспорта, перерывы в вузах. Поэтому для более полного описания изменения ситуаций понадобится совокупность (множество) моделей л = {Я, ... 2J, где Xi = Ai,Bi,jri (i — \.r} – стационарная модель передачи сообщений, описывающая «элементарную» ситуацию в системе связи. Таким образом, разработанная стохастическая модель «подвижности» трафика включает известную последовательность наблюдений O и репозитарий моделей К , описывающие изменение ситуаций в системе мобильной связи.
Прогнозирование ситуаций в системе мобильной связи
На основе прогнозирования ситуации определяется интенсивность нагрузки по виду предоставляемой услуги для каждого узла спроса.
Задача прогнозирования. На основе известной последовательности наблюдений ОДОох...о,\ и множества ситуационных моделей л = {Я, ... Я,.} необходимо определить номер ) прогнозируемой ситуации как максимум метрики РДО\ДО, то есть f = arg max (Р(0| Яу)), (1)
где Р<О\ДО – условная вероят но сть того, что для заданной модели ^j (J^v) имеет место наблюдаемая последовательность объектов ОДОох...<ДО .
Решение поставленной задачи определяется вычислением условной вероятности Р(О\ДО. Эту подзадачу нетрудно решить, используя формулу полной вероятности:
/^|яа = £^(0|МЖ5К) =
Q
= ? л b АоЛа b До-Ла ...а b т(от\
/ у Ч\ <у1 V 1/ ^^ ^2 V 2/ q3q3 Чт-\Чт Чт v т
°- (2)
где знак Q обозначает, что суммирование производится по всем счетным комбинациям последовательности состояний наблюдения. Согласно выражению (2) при прямом подсчете РДО>\ДО для самого наихудшего случая необходимо выполнить 2TNT умножений, что затрудняет прогнозирование ситуаций в масштабе реального времени. Для уменьшения количества вычислений предлагается модифицированный алгоритм «прямого хода» [2-3].
Введем в рассмотрение прямую переменную «ДО , которая определяется для заданной модели Л как значение вероятности того, что к моменту времени t наблюдалась последовательность
О = {о,;о2...о,}, и в момент t система находилась в состоянии aS *
at^ = P
Переменную а ДО можно вычислить согласно следующему алгоритму.
В п ротивном случае «у ДО = якЬкДО для всех к = ДО .
Шаг 2. Для всех 1ДО 2... Т-\ проверяется текущее состояние наблюдения. Если достоверно известен номер Г е {1;2..^} текущего со- стояния наблюдения (то есть q, = S, ), то
«ДО*^
h«,Wakl-
.^=1
ЬДОДО и «,+1(/) = 0 для
1*1*.
В противном случае
«,до=
N
^а,ДОак1
^=l
b] (ot+x ) для всех I = 1, N.
Шаг 3. Вычисление искомой вероятности
N
Р(О\ЛХ) = ^ТДО.
Трудоемкость вычисления вероятности РДОДО в данном случае меньше, так как для самого наихудшего случая (когда неизвестны все состояния наблюдений) требует порядка ТДО операций умножения.
Расчет потребной нагрузки в условиях неопределенности состояний наблюдений
Под потребной нагрузкой понимается число каналов связи, требующихся для удовлетворения услуг для каждого узла спроса. При рассмотрении каждого узла спроса как источника пуассоновского потока определение потребной нагрузки может производиться на основе методов Эрланга [3] по каждому виду запрашиваемой услуги, из анализа интенсивности «звонков»:
О = ДОо2 ...о,ДО {(oJ^XCozI^)-^!^)} •
Трудностью решения данной задачи может стать отсутствие информации о 8j – номере узла спроса поступления заявки в O .
Метод восстановления текущих состояний объектов 8, будет заключаться в выборе такой последовательности состояний Q^q^-qr} конечной длины т , которая с наибольшей вероятностью порождает наблюдаемую последовательность объектов О = {o,;o2 ...оД по заданной модели X, = (A.,B ,,k .) (идентифицированной на предыдущем этапе). Другими словами, требуется определить «наилучшую» последовательность g*=(^;^...^),макси-мизирующую вероятность РфДХЛ .
Эта подзадача решается на основе использования алгоритма Витерби (Viterbi Algorithm), являющегося вариантом метода динамического программирования [2-3] для цепей Маркова.
Шаг 1. Инициа лиз ация 8АД = кД\оД и ^i(0 = 0 для всех / = 1Л, где переменная
Шаг 2. Индуктивный переход:
-
8, Д ) = maxfcO, Д^а^ Abj (pt ), для всех j = 1, N
и t = 2,N; //t 0) = arg maxl^ WM ]. \
Шаг 3. Останов. Определение наибольшей вероятности последовательности наблюдения О = {o^-.O,}, то есть P* = max[O(z)] , которая достигается при прохождении некоторой оптимальной последовательности состояний
\
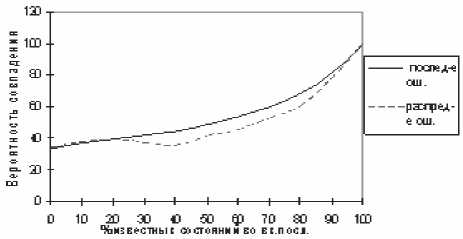
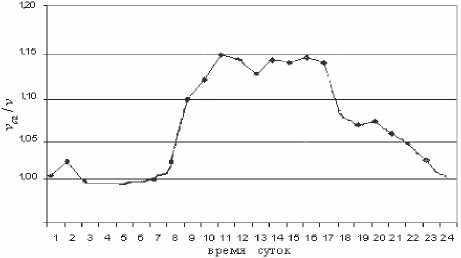
Шаг 4. Восстановление оптимальной после- довательности состояний (обратный проход): q, = ^,+1 Оптимизация канального ресурса Задачу распределения каналов между БС системы мобильной удобно рассматривать как оптимизационную, которую можно решить, например, методом линейного программирования. Задача распределения канального ресурса. Известна следующая информация: p^k*1 – число потребных каналов для обслуживания к -го узла спроса Обозначим через Xrj планируемое число каналов, которое будет использоваться I -ой БС для обслуживания k-го узла спроса. Тогда в принятых N L обозначениях будем иметь, что 2j 2j ^klXkl – об- 4 = 1 /=1 щая (суммарная) стоимость канального распреде- L ления в системе мобильной связи; У'Ху – общее число каналов, необходимых для обслуживания N k-го узла спроса; x^i – общее число разрешен- 4=1 ных каналов l-ой БС. Будем полагать, что должны выполняться условия: t,Xy=N{-',k = l,N,(3) ix'six.(5) k=\/=1 Таким образом, задачу наилучшего распределения каналов между БС можно сформулировать следующим образом: нужно найти аргументы ■^"ki , обеспечивающие минимум функционала J вида N I. J ~ 2j 2j ^klXkl при соблюдении условий (3)-(5) 4=1 /=1 и Xlk ^°. Следует отметить, что сформулированная задача аналогична так называемой открытой транспортной модели [4]. Решение поставленной задачи может базироваться на методе последовательного улучшения плана – симплексного метода [4]. Необходимым дополнительным условием решения задачи является целочисленность значений искомых аргументов Xkl . Далее, перебирая все возможные варианты конфигураций размещения БС и повторяя выше- описанную методику канального распределения, можно получить множество значений критерия J. Дальнейшим естественным шагом будет выбор и назначение той конфигурации сети мобильной связи, для которой значение критерия J (среди имеющегося кортежа-множества J) минимально. На последнем этапе составляется расписание активации каналов для каждой БС, например, топологическим методом [3]. Алгоритм уточнения (обучения) параметров моделей ситуационноадаптивного планирования В процессе эксплуатации системы мобильной связи допустимо изменение параметров 4, в„ л6 для отдельно взятой модели A' . Так, суточная плотность концентрации мобильных абонентов в деловой части больших городов является более или менее стационарной, но и она может существенно измениться на более длительном периоде наблюдения, например, в зависимости от сезонной, экономической конъюнктуры. Следовательно, возникает вопрос о разработке способов (алгоритмов) выделения (кластеризации) в отдельную группу новых ситуаций относительно существующих или, наоборот, уточнения количественных параметров старых ситуаций. Другими словами, возникает задача «обучения» моделей A , связанная с переоценкой их параметров 4, В,, Лj. Последнее приводит к модификации множества СММ л = Uw-^A. Задача переоценки параметров модели должна базироваться на достоверном знании текущей ситуации 4 и последовательности наблюдений O. При этом критерием решения задачи должна быть максимизация условной вероятности ЛО|Л) , которая повышает достоверность принятия решения о выборе именно X- -ой ситуации. Задача уточнения параметров модели. Пусть даны последовательность наблюдений О = Крх\ог...оА и модель 4 = ^а,в,л). Необходимо определить (настроить) параметры модели А, В, л, максимизирующие вероятность P(O\A) . Решение поставленной задачи базируется на алгоритме Баума-Уэлша (Baum-Welsh Algorithm) [2-3]. Для этого вводится новая переменная ^,П = Р<д,=8„Ч1+х=ВД0,Хд, которая определяет вероятность того, что при заданной последовательности O = {o1;o2...o,} мобильная система в моменты времени t и t + 1 будет находиться (обслуживать), соответственно, в состояниях (узлах спроса) 5, и SJ . Используя прямую otf ^i^ и обратную 4+1 (V) переменные, можно записать aPPa^Ao^PtAA ^',v—^—= аРра^Ьро^АР^РА ^^“t^^j^^PP-AA /=i /-I Далее вводится еще одна переменная Yt A) i являющаяся апостериорной вероятностью того, что при заданной последовательности наблюдений O система в момент времени t будет находиться в состоянии : N YPn = ^tU,n. Введенные переменные /ДР, ^,PJ) облада-r-1 ют следующими свойствами: E^xo – ожидае мое число переходов из состояния 4; УЛ^’А– ожидаемое число переходов из состояния Bj в состояние в, . На основании этих свойств получены формулы переоценки параметров СММ А, В, л, то есть, вводя уточненные значения этих параметров A ={^}, В=ДэДкА, л,имеем л =/ДЙ, л У./ЛЙС. ^=<1—, РДА=Ч---, "L/Др Т/дл Окончательно решается задача Витерби, связанная с нахождением максимального значения вероятности Р(О\ХД относительно уже уточненных значений параметров СММ – А , В, л. При этом решение задачи Витерби приводит к возрастанию функции правдоподобия, то есть р(о|4) > ло|4) • В случае, если Р(О|4)-Л<9|А)^^’Где s – достаточно малая величина, полагают, что я, = 4 , и на этом процесс переоценки параметров модели завершают. Другими словами, переоценку параметров проводят до тех пор, пока параметры не перестанут изменяться. Уточненные параметры затем можно использовать в качестве характеристик модифицированной модели 4 для решения задач ситуационно-адаптивного планирования. Рис. 1. Зависимость достоверности выбора первой модели от длины наблюдений T Рис. 2. Оценки вероятностей совпадений входной и восстановленной последовательности наблюдений в зависимости от их неопределенности Рис. 3. К оценке эффективности использования алгоритмов ситуационно-адаптивного планирования Заключение Апробация алгоритмов ситуационно-адаптивного планирования проводилась в режиме тестовых испытаний сети широкополосной свя- зи WiMax в г. Уфе. В качестве оценки качества алгоритмов исследовалась зависимость длины T наблюдаемой последовательности объектов на достоверность определения текущей модели наблюдения (см. рис. 1) для четырех узлов спроса. На рис. 2 приведен график зависимости вероятности восстановления входной последовательности от характера распределения неопределенных узлов спроса в наблюдаемой последовательности О = {о^.-О,}. Для оценки эффективности методов ситуационно-адаптивного планирования в целом использовалось отношение средних скоростей VeJV «закачки» данных при подключении к сети Internet (см. рис. 3), где vc – скорость обмена данными при использовании алгоритмов планирования, V – без использования. Из рис. 3 видно, что в часы наиболее интенсивной нагрузки наблюдается увеличение скорости обмена сообщениями на 15% при использовании рекомендаций методологии ситуационно-адаптивного планирования. Отметим также, что все этапы ситуационно-адаптивного планирования достаточно хорошо формализованы, что говорит о возможности их применения в составе управляющего программного комплекса мобильных систем широкополосной связи.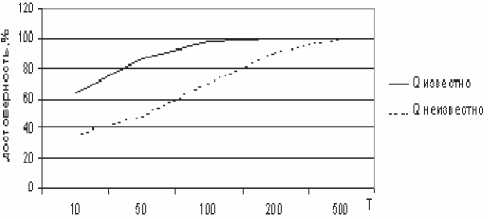
Список литературы Модели, задачи и алгоритмы ситуационно-адаптивного планирования радиоресурсов систем мобильной широкополосной связи
- Шорин О.А. Методы оптимального распределения частотно-временного ресурса в системах подвижной связи. Автореферат диссертации д.т.н. М.: МТУСИ, 2006 -24 с.
- Рабинер Л.Р. Скрытые марковские модели и их применение в избранных приложениях при распознавании речи//ТИИЭР. Т. 77, № 2, 1989. -88 с.
- Султанов А.Х., Кузнецов И.В., Блохин В.В. Сигнальные и структурные методы повышения информационной емкости телекоммуникационных систем. М.: Радио и связь, 2006. -325 с.
- Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982. -457 с.


