Modeling Epileptic EEG Time Series by State Space Model and Kalman Filtering Algorithm

Published Online February 2014 in MECS

The electroencephalogram (EEG) measures the electrical activity of the brain by applying electrodes on the head surface which was firstly introduced by Berger [1]. It is a non-invasive technique and there has been an explosion of popular and scientific interest in measuring and analyzing it in many fields related to neuroscience (physiology, psychology, neurology, psychiatry, etc.) [2].

With regard to the diagnosis and localization of pathological processes involved in epilepsy, the recordings of brain activity by means of EEG have become widely important.

One of the most disabling aspects of epilepsy is the sudden, unforeseen way in which epileptic seizures strike. Apart from the risk of serious injury, there is often a severe feeling of helplessness that has a strong impact on the everyday life of a patient [3]. The word ‘epilepsy’ is derived from the Greek word epilambanein, which means ‘to seize or attack’. It is now known, however, that seizures are the result of a sudden, usually brief, excessive electrical discharge in a group of brain cells (neurons) and different parts of the brain can be the site of such discharges. Transient symptoms can occur, such as loss of awareness or consciousness and disturbances of movement, sensation (including vision, hearing, and taste), mood, or mental function.

EEG signal modeling is important to achieve a better understanding of the physical mechanisms generating these signals and to identify the causes of changes in EEG signals [4]. Modeling can also be used for predicting the future neurological outcome and for data compression. In addition, simulations based on the models of EEG signals can be used to demonstrate the effectiveness of a certain quantitative analysis method or EEG feature extraction.

In order to improve the estimation of noisy physiological signals, different methods have been employed. Some of these methods consist of machine learning technique [5], averaging [6] and Kalman filtering [7, 8]. Machine learning techniques can detect artifacts efficiently but in this method large amount of data is required. Averaging methods can reduce the noise levels, but it smooths the signal fluctuations. Compared to these techniques, Kalman filter (KF) methods can estimate the trends of biological signals [9].

The properties of KF along with the simplicity of the derived equations make it valuable in the analysis of signals. In another study [10] an off-line Kalman filter approach to remove Transcranial Magnetic Stimulation (TMS) induced artifacts from EEG recordings is proposed. Lenz et al. [7] made use of a modified unscented Kalman filter and a corresponding unscented smoother for the estimation of the underlying neural activity of the brain. Purdon et al. [11] have developed a state space approach for multimodal integration of simultaneous EEG and fMRI. Li et al. [8] evaluated a new robust tracking algorithm for estimating blood pressure and heart rate (HR) based upon a Kalman Filter with an update sequence modified by the KF innovation sequence and the value of the Signal Quality Index (SQI). In the study of Mneimneh et al. [12] an adaptive Kalman filter is proposed for the real time removal of baseline wandering using a polynomial approximation independent of the signal characteristics. Bohlin [13], Mathieu [14], Dusquesnoy [15], Blechschmid [16] and Jansen et al. [17,18] have already applied Kalman filtering to an AR model for analyzing EEG signals.

Despite these works and the theoretical advantages (optimal filter, non-stationary spectral analysis), Kalman filtering was not very much used for EEG analysis and modeling in a specific neurological and pathological disorders. It can be assumed that the unsolved problem of selecting the model order and the unstable estimation algorithms were reasons for this.

From the multiplicity of concepts and methods for time-series analysis that have been applied to neuroscientific time-series, this study focused on predictive modeling, i.e., finding a predictor for future time-series values, based on present and past values. More precisely, we will discuss a particular class of predictive modeling that is attracting considerable attention due to its wide applicability: the state-space model [4, 19-22] and Kalman filter. In this study, a state space model is used to distinguish between the underlying brain states and the EEG measurements in epileptic patients. In addition, we make use of a Kalman filter for the estimation of the fundamental neural activity.

The paper is structured as follows. In the next section, the signals and methods (state space model and Kalman filtering) used in this study are briefly described. Then, the results of analysis on data sets are presented. Finally, some results of EEG data are discussed.

• II.    Methods2.1    Data Selection

Five sets (denoted A–E) each containing 100 single channel EEG segments of 23.6-sec duration, were collected by Andrzejak et al. [23, 24]. These segments were selected and cut out from continuous multichannel EEG recordings after visual inspection for artifacts, e.g., due to muscle activity or eye movements.

Sets A and B consisted of segments taken from surface EEG recordings that were carried out on healthy volunteers using a standardized electrode placement. Volunteers were relaxed in a conscious state with eyes open (A) and eyes closed (B), respectively. Sets C, D, and E originated from the EEG archive of pre-surgical diagnosis [23, 24].

Segments in set D were recorded from within the epileptogenic zone, and those in set C from the hippocampal formation of the opposite hemisphere of the brain. While sets C and D contained only activity measured during seizure free intervals, set E only contained seizure activity. Here segments were selected from all recording sites exhibiting ictal activity.

All EEG signals were recorded with the same 128-channel amplifier system, using an average common reference [omitting electrodes containing pathological activity (C, D, and E) or strong eye movement artifacts (A and B)]. After 12 bit analog-to-digital conversion, the data were written continuously onto the disk of a data acquisition computer system at a sampling rate of 173.61 Hz. Band-pass filter settings were 0.53–40 Hz (12 dB/oct) [23, 24].

In this study, 40 EEG signals from sets A and E were used in order to model EEG behaviors in normal and seizure states. These two types of EEG signals are shown in Fig. 1.

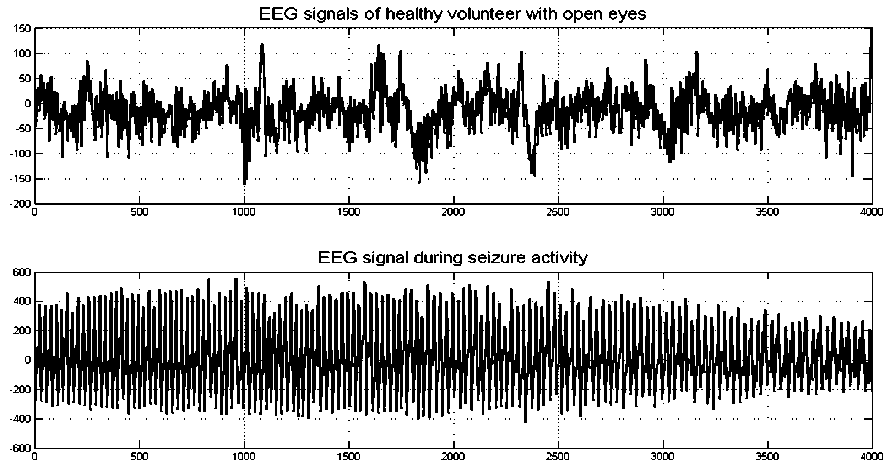
Fig. 1: Electroencephalographic signals. (Top) Healthy volunteer with open eyes. (Bottom) Epileptic patients during seizure activity

• 2.2    Spectral Estimation

The goal of spectral estimation is to describe the distribution (over frequency) of the power contained in a signal, based on a finite set of data. Estimation of power spectra is useful in a variety of applications, including the detection of signals buried in wideband noise.

In general terms, one way of estimating the PSD of a process is to simply find the discrete-time Fourier transform of the samples of the process (usually done on a grid with an FFT) and take the magnitude squared of the result (MATLAB version 7.0 with Signal Processing Toolbox). This estimate is called the Periodogram. The Periodogram estimate of the PSD of a length-L signal x L [n] is

_ˆ           X L ( f )²

PXX(f )       r T fsL

Where

L - 1

Xl (f) = 2 XL [ n ]e 'j / f5

n = 0

The actual computation of X L (f) can be performed only at a finite number of frequency points, N, and usually employs the FFT. In practice, most implementations of the Periodogram method compute the N-point PSD estimate

Pt [ A ] =

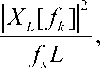
fk = f, k = 0,1,..., N -1

Where

N - 1

Xl [ fk ] = 2 X L [ ⁿ ]^e    jkn / N                  (4)

n = 0

It is wise to choose N > L so that N is the next power of two larger than L. To evaluate X L [f k ], we simply pad x L [n] with zeros to length N. If L > N, we must wrap x L [n] modulo-N prior to computing X L [f k ].

• 2.3    State Space Model

• 2.4    Kalman Filtering

A state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations. To abstract from the number of inputs, outputs and states, the variables are expressed as vectors. Additionally, if the dynamical system is linear and time invariant, the differential and algebraic equations may be written in matrix form. The state space representation (also known as the "time-domain approach") provides a convenient and compact way to model and analyze systems with multiple inputs and outputs.

The most general state-space representation of a linear system with p inputs, q outputs and n state variables is written in the following form:

X (t ) = A(t ) x ( t ) + B (t )u ( t ) y ( t ) = C (t ) x ( t) + D (t )u ( t )

where x(.) is the state vector, x(t)e^n, y(.) is the output vector, y(t)e^q, u(.) is the input or control vector, u(t)e№, A(.) is the state or system matrix, dim[A(.)] = n×n, B(.) is the input matrix, dim[B(.)] = n×p, C(.) is the output matrix, dim[C(.)] = q×n, D(.) is the feed through (or feed forward) matrix (in cases where the system model does not have a direct feed through, D(.) is the zero matrix), dim[D(.)] = q×p, and x=(t) := dx(t)

dt

The properties of KF along with the simplicity of the derived equations make it valuable in the analysis of biological signals. The Kalman Filter is an estimator with interesting properties like optimality in the Minimum Mean Square Error (MMSE).

The aim of the Kalman filter is to estimate the state vector x_k. A process of estimation which keeps pace with the data by generating an estimate of the current state vector x k with each new observation z k is described as filtering . The retrospective enhancement of a state estimate using data which has arisen subsequently is described as smoothing . The estimation of a future state vector is described as a prediction .

The Kalman filter is an optimal state estimation method for a stochastic signal [25,26] that estimates the state of a discrete time controlled process, x, with measurement data z, where x and z are governed by the linear stochastic difference equations xk = Axk-1+ Buk+ wk-1             (6)

z k = ^Hxk ⁺ v k                          (7)

The random variables w and v are independent, white, and possess normal probability distributions, p(w) ∼ N(0, Q) and p(v) ∼ N(0, R). The matrices A, B, H are the coefficient state transition matrices, Q is the state noise covariance, R is the measurement noise covariance and u is an optional control input to the state x.

The KF algorithm is given by the following equations:

5c - = Act k - 1 ^{+ Bu} k                            (8)

Pk = AP k - 1 A T + Q		(9)
K k = P k" HT ( HP k H T	+ R ) - 1	(10)
*k = * k + K k ( z k -	HX - )	(11)
P k = ( I - K k H ) P k -		(12)

P k and P k are the error covariance of a priori and a posteriori estimate, r k = Z k - Hx - is the measurement innovation (or residual) and K k is the gain required to minimize the a posteriori error covariance, P k .

The Kalman filter algorithm is presented in Fig. 2.

where x k and x k are a priori and a posteriori state estimate before and after a given measurement z k ,

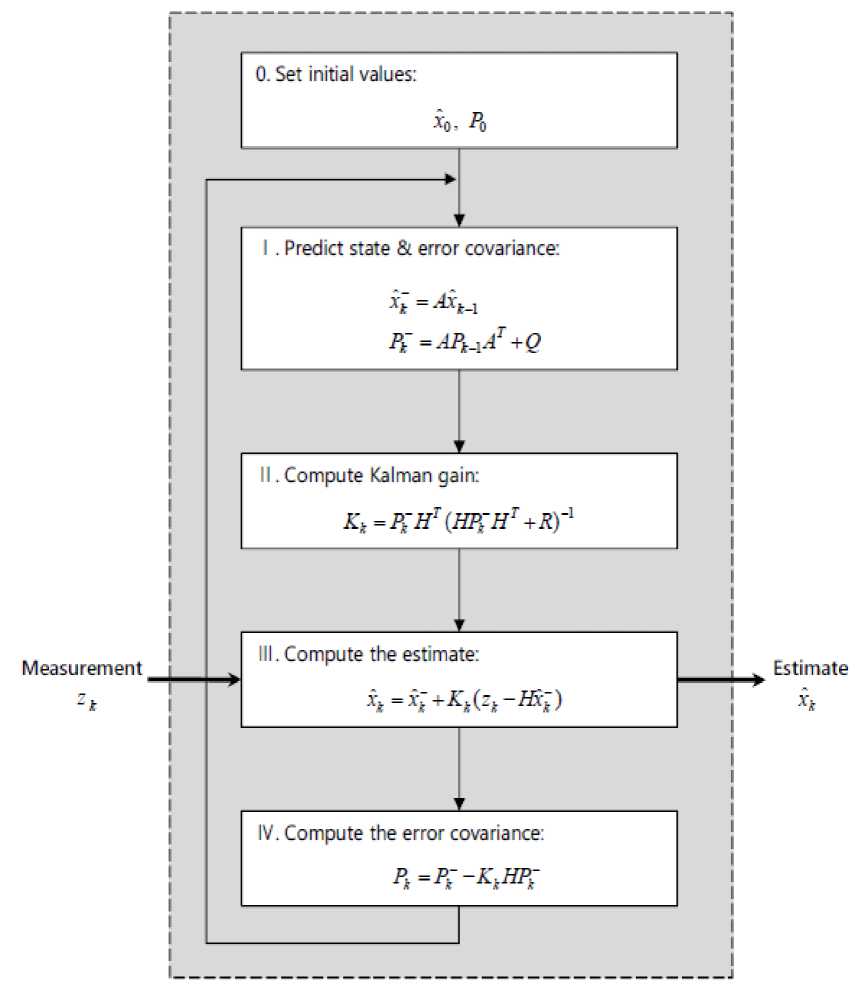
Fig. 2: Kalman Filter Algorithm [27]

In Fig. 2, the part in the dashed box is a Kalman filter algorithm. This structure receives only one input (measurement, Zk) and returns one output (estimate, xˆk ). Internal process is done through a four-step computation as discussed above.

The general idea of the Kalman filter is to propose a model for the observations, in most cases linear, where some parameters must be estimated. To be able to apply the Kalman Filter or the Kalman Smoother the model for the observations must be written in a state – space form. A state – space model is represented by two equations. One equation describes the evolution of the parameters, and second equation describes the relation of the parameters with the observations.

• III.    Results

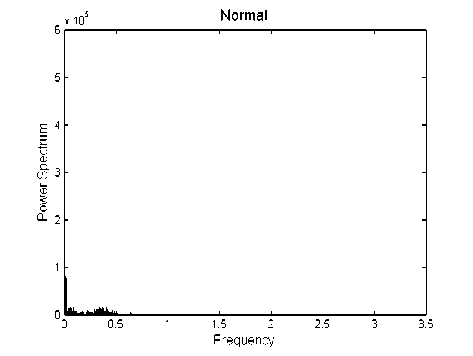
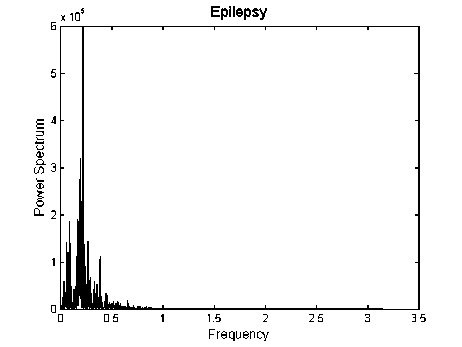
In order to study the effect of epilepsy on brain activity, the power spectrum is calculated for each of the EEG signals using Periodogram method. The power spectrum of EEG signals for the two conditions (normal and epileptic) is shown in Fig. 3.

(a)

amplitude of the power of EEG signals is increased during epilepsy.

Fig. 4 shows the amplitude of the first peak power of EEG signals in normal subject and epileptic patients.

It can be observed from these figures, that the prominent peaks are not at similar frequencies. There is a single narrowed band peak with high amplitude in the power spectrum at around 0.25 Hz as an example shown in Fig. 3(b). Whereas, for the normal subject, there are several spectral peaks spreading throughout the frequency ranges. Furthermore, the amplitude of these components is lower than that of during epilepsy (as an example shown in Fig. 4).

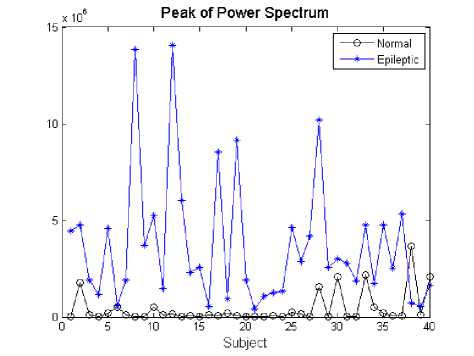
Fig 4: Amplitude of the power spectrum in normal subjects and during epilepsy

A new method for modeling and estimating the normal and epileptic EEG signals is described based on a state-space model and the Kalman filter.

(b)

Fig. 3: Power spectrum of EEG signals. (a) Normal subject, (b) Epileptic patient

Results presented in Fig. 3 show that the power spectrum of EEG signals in the normal state and in the epileptic state is remarkably different. In addition, the

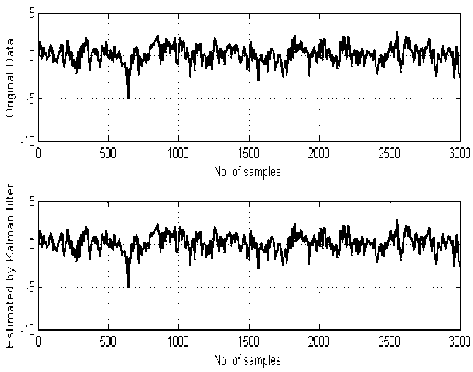
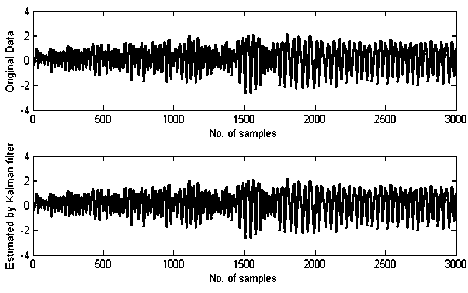
Fig. 5 depicts the raw and estimated signal by applying the proposed approach in two data sets: (a) normal subjects, (b) epileptic patients during seizure activity.

(a)

(b)

Fig. 5: The original EEG signal (top panel) and the estimated signal using proposed method (bottom panel). (a) Healthy volunteer, (b) Epileptic patients during seizure activity

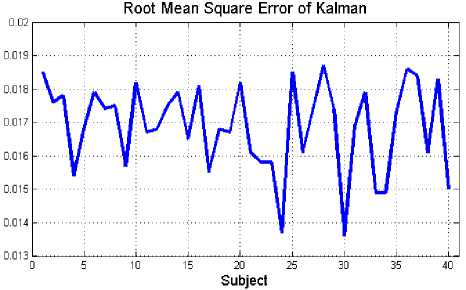
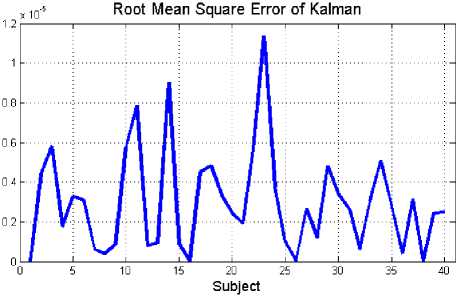
The estimation performance of the proposed method on EEG signals is evaluated using the root mean square (RMS) measurement. The RMS is a good criterion to compute the quality of estimation algorithm that has been implemented. With RMS measure, the difference between the original EEG signal and the estimated signal can be compared. The results of this evaluation for healthy volunteer and epileptic patients during seizure activity are summarized in Fig. 6(a) and Fig. 6(b), respectively.

(a)

(b)

Fig. 6: Estimated error (RMS) between original and estimated data for 40 subjects: (a) healthy subjects, (b) epileptic patients during seizure activity

According to the values of the RMS (Fig. 6(a) and Fig. 6(b)), it is obvious that by applying this method, EEG signals could be estimated accurately. The mean estimation error for this method on healthy individuals and epileptic patients are about 0.0169±0.0013 and 2.98×10-6±2.58×10-6, respectively.

• IV.    Discussion

The variations of EEG signals can be separated into different components by use of spectral analysis. The frequency domain analysis of EEG signals reveals that the pattern of the power spectrum is remarkably different during epilepsy than that of the normal subject. In addition, the power of EEG signals is increased during epilepsy. There is a single narrowed band peak with high amplitude in the power at around 0.25 Hz as an example shown in Fig. 3(b), but for the normal, there are several spectral peaks spreading throughout the frequency ranges. Furthermore, the amplitude of these components is lower than that of during epilepsy (as an example shown in Fig. 4).

The application of Kalman filters and the state space model for estimation of pathological EEG signals is new to the best of our knowledge.

In this paper, it is assumed that EEG time series are vectors valued with random process and have slow dynamic variabilities during the specific time. In addition, past realizations have some information which is relevant to future realizations and these changes can be modeled with a state-space model. It has shown that the Kalman filter is considerably robust and it has a low sensitivity to suboptimal parameter setting. Generally speaking, this feature of the Kalman filter is very important in a clinical environment, since the optimal setting is impossible to determine. The Kalman filter is more than just a filter since it holds the potential to incorporate more information about the EEG generating process in the model, maintaining the dynamics in the signal and producing accurate estimates.

In the normal stage, the cortex is more active and more neurons are available for processing [28]; whereas, in epileptic stage, the cortex becomes inactive and EEG signals become less random. The neurons in the cerebral hemispheres during the seizure misfire and create abnormal electrical activity. Therefore, the number of neurons available for processing the information reduces during the seizures. In other words, the variability of epileptic activity was less as compared to that of non-epileptic activity [29,  30]. It was supported by the reduced dimensionality of epileptic seizures as compared to non-epileptic EEG signals. This concept finds support in the observations that neuronal hyper-synchrony underlies seizures: a phenomenon during which the number of independent variables required to describe the system was smaller [31].

Morbidi et al. [10] show that by applying Kalman filter the effect of the magnetic artifacts on the EEG recordings has been strongly reduced, while preserving the integrity of EEG signals around TMS impulses. The result of Mneimneh et al. [12] shows that the Kalman filter approach was successful in the online estimation and removal of the baseline wandering for real-patient and a simulated test signal.

In this study, a state space model is used to distinguish between the underlying brain states and the EEG measurements in epileptic patients. In addition, we make use of a Kalman filter for the estimation of the fundamental neural activity.

The performance of the presented approach is evaluated using the root mean square (RMS) measurement to produce a reliable estimation of real EEG signals. The RMS is a good criterion to compute the quality of estimation algorithm that has been implemented. According to the values of the RMS (Fig. 6(a) and Fig. 6(b)), it is obvious that by applying this method, EEG signals could be estimated accurately. Therefore, this model is appropriate for the analysis of EEG recordings. In fact, this model is capable of predicting changes in EEG time series with phenomena such as epileptic spikes and seizures.

The results presented here might be of some use in addressing the issue of stochastic dynamics versus chaos in the nervous system. In recent years, there has been a tendency to view the EEG as the output of a low dimensional dynamic system with chaotic behavior [32,33]. An extreme point of view even banishes stochastic effects as an explanation for the EEG signals. The availability of parametric nonlinear models may be of assistance in assessing the role of stochastic effects in the EEG as well as to characterize the multiple dynamical attractors of the nervous system, some of which may or not be chaotic [34,35]. Further works can be considered the nonlinear behavior of brain activity in the modeling of EEG signals.

• V.    Conclusion

The results of this study showed that applying the state space model and Kalman filter could be useful to estimate EEG signals. In addition, this algorithm can be applied to other non-stationary biological systems, too.

EEG time series are usually recorded from a set of electrodes covering the whole scalp. The method which has been proposed in this paper could be applied independently to each channel of the data, but it would be desirable to have a modeling approach capable of building a single common model from all available channels simultaneously; thereby also the spatial information contained in the positions of electrodes could be incorporated. The generalization of the method to this case will be the subject of future work.