Modeling Interaction in the Educational Process is a Tool for Improving its Effectiveness
Автор: Nataliya Mutovkina, Zhongfeng Pan
Журнал: International Journal of Modern Education and Computer Science @ijmecs
Статья в выпуске: 3 vol.16, 2024 года.
Бесплатный доступ
In the context of growing and widespread demand for higher professional education, an important aspect is the quality of the educational process and the effectiveness of its results. The educational process is a complex socio-economic phenomenon involving at least two parties – the teacher and the students. It is these subjects of the process that are the key elements and interact, as a result of which there is an increase in the amount of information that is transformed into a competency-based form. It is the acquisition by students of the competencies they need in their professional activities that is the goal of the educational process. As a result of the study, it was found that it is possible to optimize the educational process and fill it with the necessary educational elements through fuzzy modeling of the transmission and perception of educational information. The article proposes a model of fuzzy interaction between a teacher and a student group. The model is designed to determine the possibilities of optimizing the educational process and the optimal combination of educational elements. Educational elements include teaching materials, communication tools, and digital technologies. With the help of these elements and the pedagogical strategy, the transfer of educational information to students is carried out. The same means and motivation are used for the perception of educational information. It is important to find the optimal combination of educational elements and tools that contribute to the effective transfer and assimilation of educational information. Improving the effectiveness of interaction between teachers and students affects the quality of education. The quality of the educational process determines the level of students' training, the success of graduates' professional activities, and the professional self-realization of teachers. The interaction model makes it possible to improve the quality of the educational process. This is confirmed by the results of its application at Tver State Technical University.
Educational Process, Interaction, Teachers, Students, Coordination of Interests, Fuzzy Logic
Короткий адрес: https://sciup.org/15019171
IDR: 15019171 | DOI: 10.5815/ijmecs.2024.03.06
Текст научной статьи Modeling Interaction in the Educational Process is a Tool for Improving its Effectiveness
The educational process is a complex socio-economic phenomenon, finite, provided that a specific level of education, in which the major participants are students and teachers. The purpose of the educational process is for students to master educational material and gain knowledge, skills, and abilities that are necessary for the development of professional competencies. It is professional competencies that enable graduates to carry out professional activities accompanied by career growth. As the long-term practice of the author’s teaching work shows, the more intense and interesting the educational process, the more information the student remembers, and the more actively the formation of specified competencies takes place.
The effectiveness of the educational process is determined by the extent to which students will attain primary general cultural and professional competencies. The success of the graduates’ professional activities depends on this. The development of educational material and the formation of competencies largely depend on the degree of contact between the student and the teacher in the learning process. It is mutual understanding and conducting classes in a friendly, psychologically comfortable environment that makes the learning process the most productive. The educational process is characterized by subject-to-subject interaction, the impact is manifested both by the teacher and by the student. The object of this system is educational information. It is a kind of “conductor” of interaction. Educational information is considered a system of interrelated elements, the main of which are lectures and their presentations, practical and laboratory classes, and methodological materials. The methodological materials contain explanations for the implementation of practical and laboratory tasks, and examples of solving typical tasks and test tasks. In addition, the educational process provides for students to complete coursework and practice outside the university. All these components are interconnected. It should be borne in mind that educational information is updated and supplemented over time because of the emergence of new knowledge, technologies, etc. There is a problem with the timely and effective transfer of relevant information to students. Besides, the continuation of the problem of information transmission is the problem of its perception by students. To solve these problems, it is necessary to determine the factors influencing the educational process. Factors can be positive and contribute to improving the effectiveness of the educational process. This is an investment in the educational process, and not just financial. The second group contains destructive factors, which are divided into internal and external interference. The author, based on statistical data accumulated over the past 14 years, has developed a model of interactive interaction between a teacher and a student through the transmission and perception of educational information. The goal is to increase the effectiveness of the educational process. As statistical data, fuzzy estimates of the effectiveness of the transmission and assimilation of educational information in several student groups were used with various combinations and the influence of positive and negative factors. The impact of the factors was also expressed using fuzzy estimates. Thus, this study aims to test a model of interactive interaction between a teacher and students in different conditions of factor influence to develop recommendations for improving the effectiveness of the educational process.
2. Theoretical Aspects of the Study 2.1. Literature Review
The problem of improving the effectiveness of the educational process does not lose its relevance to this day. The emergence of new forms of interactive interaction between teachers and students, the introduction of distance learning, and a large increase in the volume of information broadcast by teachers lead to the need to develop new forms of mastering this information, adapting students to rapidly changing learning conditions. For example, in [1] the authors draw attention to the problem of inappropriate use of digital devices and information technologies by students. Students actively use information technology, but mainly for entertainment and activities unrelated to the educational process. In the article [2], the authors concluded that, in general, applicants have skills in using digital technologies in education, but they differ in level. It is possible to identify groups of applicants with low rates of mastering digital technologies and skills in their use. This is usually explained by the different levels of training of students in urban and rural areas [34]. Accordingly, the solution to the problem can be the timely distribution of first-year students into groups according to their knowledge of information technology and the organization of separate classes. This solution is also suitable for other disciplines, for example, a foreign language.
There is also a problem of insufficient information on the educational process in educational organizations. For example, in the article [5], the authors point out the ambiguous nature of using information technology in the educational process. On the one hand, information technologies contribute to activating students' interest in learning and make the learning process more flexible. However, problems arise in the development of teaching methods necessary to stimulate learning activities.
In several works [6-9], the authors explore the application of blended learning, when digital technologies are used along with traditional teaching methods. Digital departments can also help overcome the difficulties of introducing information technology into the educational process. Digital departments are responsible for ensuring the successful application of information technology in education. The positive experience of creating digital departments is described in [10]. Here, questions arise: What kind of educational material can be broadcasted through electronic information channels? What part of the course should be studied in the classroom? What initial skills should students have at the same time?
The effectiveness of the “transmission ↔ perception” system directly depends on the organization of the educational process, the presentation of educational material, and the psychological climate in the “teacher ↔ students” system.
This system is more extensive than the “transmission and perception” system since it affects not only the educational process but also activities that teachers and students can conduct together: visiting scientific and educational forums, participating in Olympiads, scientific and practical conferences, sports events, etc.
-
2.2. Teacher-Students Interaction System
In any interaction system, both direct and feedback are important. The teacher, acting as a translator of educational information, must understand how this information is understood by students. Figure 1 shows a system of interaction between a teacher and students without the use of elements of digitalization in the educational process and the introduction of interactive elements. This is a traditional system of interaction used in educational organizations.
There is a teacher here (T), there are many components of the educational process into which investments are transformed;
H
j
(t)
there are hindrances that reduce the effectiveness of educational components; there is a student group;
x(t)
there are planned effects, activation of the teacher’s efforts, his work plan;
v(t)
there are teacher’s influences on creating elements of the educational process (lectures, practices, laboratory work, test assignments, etc.);
y
*
(t)
is the impact of transferring the content of educational components to the student group;
y(t)
is the transfer of information based on the results of perception analysis (PA) and benevolence analysis (BA). By the analysis of perception, the author means the analysis of the effectiveness of mastering educational material, and by the analysis of benevolence – the general attitude of students towards the teacher. The results of the analysis are the adjustments of Ay(t), which the teacher converts into improved effects of
y(t).
New influences should promote an open, constructive dialogue between the teacher and students.
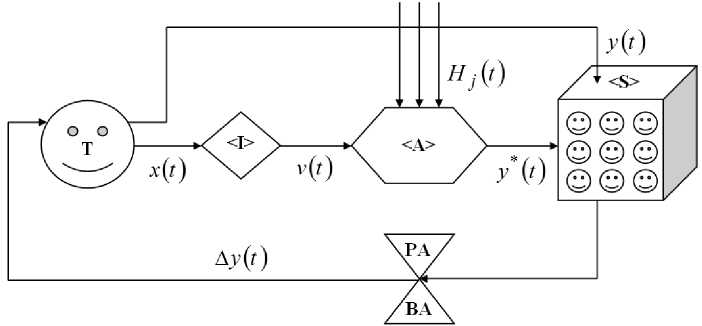
Fig. 1. The traditional system of teacher-students interaction.
One of the primary mechanisms that can help in reducing negative factors affecting the educational process is information technology and systemic digitalization of education. Figure 2 shows a diagram of interaction between a teacher and students, taking into account the introduction of digital services into the educational process. Information technology is designed to monitor the negative impact of interference and inform the teacher about it.
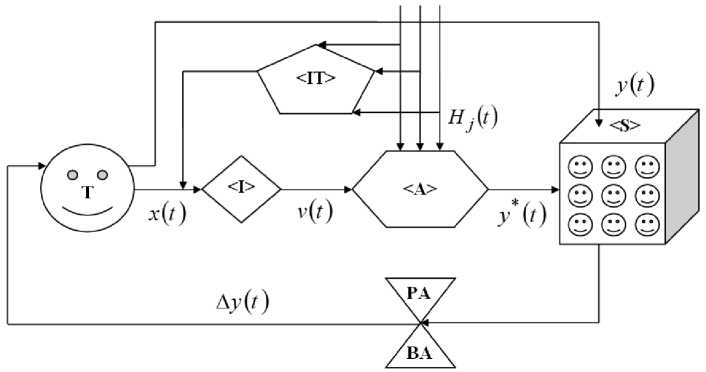
Fig. 2. The scheme of interaction taking into account digitalization.
Here, the teacher will respond to threats in a timely manner and plan the effects of x(t) taking into account possible interference. The introduction of information technology will reduce the values of Ay(t) to almost zero, which means it will reduce the burden on teachers, relieve tension between the teacher and the student group and thereby optimize the learning process.
Evaluation and feedback mechanisms are important components of effective teaching in higher education institutions and are constantly monitored. The annual survey of student satisfaction with the educational process at Tver State Technical University collects information about students’ perceptions of these aspects and problematic results in order to help an educational organization identify its weaknesses, amend its strategies and improve teaching effectiveness.
The feedback study can be performed through regression analysis, as suggested in the article [11].
In this study, the author is based on the results of a survey of students in economics. The author conducts a survey every semester after the introduction of new elements into the educational process, for example, interactive lectures, subject-oriented colloquiums, joint classes with students of different courses and other targeted components of the educational process. The study examines student academic performance in relation to the dynamics of interest in the course. It was found that the more interesting the classes, the higher the academic performance.
2.3. The Relevance of Using Fuzzy Logic
3. Modeling Teacher-Students Interaction
The relevance of using fuzzy logic is because of the tendency to increase the complexity of mathematical and formal models of actual management systems and processes, the desire to upgrade their adequacy, and take into account many factors influencing decision-making. Fuzzy sets allow you to work with objects that do not have clear boundaries. Such an object is the educational process. It consists of numerous supporting elements that can be structured depending on the specifics of the course being taught and the personal characteristics of the students. It is necessary to take into account the influence of both motivating components and factors that interfere with productive interaction between the teacher and the student group.
To build a model of interactive interaction, we will use the following notation. ED is the amount of educational information transmitted in one classroom session. As practice shows, a teacher cannot transfer less than 6.1% and more than 23.8% of the total volume of the training course in one lesson. Deviations both to the lesser and to the greater side are methodologically impractical and create obstacles. Interference occurs as a lack of information for solving problems and practical situations, or as overwork of students, reducing their attention when transmitting too much information to them. We will take lectures as A 1 , lecture presentations and methodological guidelines for studying the course are A 2 , assignments for practical and laboratory classes are A3, and tests are A4. We will designate many activities that contribute to the transfer of educational information as / 1 , and we will take many activities to support the motivation of students to master educational information as / 2 . Various hindrances act as factors hindering the successful transmission and perception of educational information, which we denote by H 1 and H 2 , respectively. Because of observing the implementation of the educational process, additional sets can be formed from the original sets. For example, the transmitted educational information has a set of A5 = A 1 U A 2 , a lot of completed practical works has A 3 c A3, and a set of completed test tasks has A 4 C A4. In addition, many students have revealed the presence of internal incentives to master educational information (A6). The strength of these incentives depends on the inner self of each student, and on the student’s understanding of the need to receive an education in the chosen field [12].
The sets 1 1 , 1 2 , H 1 , and H 2 influence the lots, which are the main components of distance learning.
All the listed fuzzy sets are connecting by fuzzy relations with the corresponding membership functions nRk £ ^^^^^^^^^^^^^^^^^^^^^^”
[0, 1], k = 1, 3:
R 1 = {((/ 1 , A 1 ), U r i (1 1 , A 1 )).....((/ 1 , A 4 ), U r i (1 1 , A 4 ))}, (1)
R 2 = {((H 1 , A 1 ), U r2 (H 1 , A 1 )).....((H 1 , A 4 ), U r2 (H 1 , A 4 ))},
^ 3 = {( ( A1, A2), HR3(A1 , A2)) <■< ( ( A3, A4), ЦR3 ( A3, A4 ) )}
The first ratio of (1) means that each element of educational information listed above is differently influenced by investments in the educational process (/ 1 ). The second relation relates the components of the learning process to interference (H 1 ). The third relation shows the connection between the components of the educational process. It is indisputable that all elements of the educational process are interdependent. This relationship is taken into account when building an interaction model. The relationship between the components A 1 , A 2 , A3, A4 is described by expression (2):
A 2 = f(A 1 ), A 3 = f(A 1 , A 2 ), A 4 = f(A 1 , A 2 , A 3 ) (2)
Next, the concept of the potential of an element of educational information is introduced. Potential in this case refers to the ability of a component of educational information to influence the improvement of the effectiveness of the educational process and its role in the transmission and perception of learning information. It has been established that the potential of each element depends on the initial amount of educational information (ED), the strength of the influence of factors, as well as on the potential of the input component. By this conclusion, the potentials of the elements are calculated using the following formulas:
P a i = (Я о +_5У -^ = тах{цВ 1 (ED, / 1 ) - h r2 (H 1 , A 1 ), 0}, (3)
U b 1 (ED, / 1 ) = U r0( ED, A 1 ) + h r 1 (/ 1 , A 1 ) - U r0 (ED, A 1 ) • nR1(/ 1 , A 1 )
Pa2 = (41 + R1) -B2 = тах{цВ2(А1, l) - №02^1, А2), 0},
В 2
№ В2 (/ А! , 1 1 ) = РА1+ № 01 (/ 1 , А1 ) - РА1
• № 0 1 (1 1 ’ А2 )
Pa3 = Q.' + PaJ +р1—р2 = тах^в^, рА2, /1) — №r2(H1, А3), 0},
№й2(РА1, Р.2) = Р.! + Ра2 — Р.! • Ра2,
Щв^, Р. 2 , hl = № b 3 (P a i , Р а 2)+№0 1 (! 1 ’ А з ) — № В з (Р . 1 , Р а 2) • №0^1. А з )
Ра^ = (Вз+Ра3) + R1-R2= тах{цВб(РА!, Р.2, Pa3, /1) — №r2(H1. А*). 0},
' В3
В6 ~
№В3(В3, РАз) = PAi®A2 + РАз — PAi®A2 • РАз'
№ в 6 (Р а 1 , р . 2 , Р а з , / 1) = № В 3 (В з , Р а 2) +№ 01 (1 1 . А^-^В з , Р а 3) • №0^1 . А * )
The potentials of the components А 3 , А * , А 5 , А6 can be founding when using the formulas:
Pa6 =R1-P2= тах{№01(/2, А6) — №r2(H2. А6), 0}
Pas = (Pa2 + Pa2) + Pa6 —R2= тах{№в7(Вз, Pa6) — №o2(H2. А5), 0},
' В 3
В7
№ B 7 (B 3 , Р А6) = Р А 1 ®А2 + P A6 — P A i ®A2 • P A6
Pa3 = (Pas+PaJ -R2= тах{№в8(РА5, Pa6) — №r2(H2, А3), 0},
B8
№Ва(РА3, РА6)=РА3+РА6—РА^РА6
Pa4 = ((Pas + Pa6) + Pa3) -R2 = (В8+Ра3) -R2= тах{№в9(Вв, Pa3) — №о2(»2, А*), 0}, (10)
B 9
№ В д (В 8 , Р А З ) = Р А5фА6 + Р А З — PAS®A6 • Р А З
Knowing the potentials of the components and the factors that affect the values of the effectiveness, you can determine the coefficients of the mutual influence of the elements. Management impacts, in this case, consist of varying not only external impacts (which is often quite difficult) but also in changing internal coefficients of influence. In practice, this can be expressed in improving the structure and content of the work program of the discipline, optimizing the composition of methods and means of teaching it, and so on.
-
3.1. The Model of Information Transmission
The information transfer model is basing on the following assumptions:
-
• The investments / 1 should lead to an increase in the overall information transfer rate, that is, increase the overall potential of the model. Active independent work of the teacher, deep awareness of their intellectual activity should also help to increase the transfer rate of educational information;
-
• The presence of external interference H 1 leads to a decrease in the volume and quality of transmitted information;
-
• The value of the total potential also depends on the initial amount of information already transmitted.
The total potential of the information transfer model is determining by the formula:
KTI = (((Pai +Pa2) + (Раз + Pa4)) + R1) — R2 (11)
The coefficients of mutual influence of the components can found from the system of equations:
PA i - 1 - {/Й з (аъ А 2 )фЙ з (А 1 , А3) ( Л1 , A 2 , Лз ) + ^ аз (А 1 , ^ 4 )} Р а 2 - ^ Й з ( ^ 1 , А 2 ) - ^ R3(a2, А3)фЙ3(А2, А 4 ) (А 2 , ^ 3 , ^ 4 ) Р а 3 - /Й з (А1, А з )®Й з (А2, А з )( ^ 1 , ^ 2 , ^ 3 ) -/Й з ( ^ 1 , ^ 4 )
< РА 4 — / И 3 (а 1 , А4)фЙ3(А2, А4) (^ 1 , ^ 2 , ^ 4 ) + ^ Йз^З , ^ 4 )
The visualized information transfer model is present in Figure 3 as a fuzzy-oriented graph, the weights of the arcs, which are the values of the corresponding membership functions. In Figures 3 and 4 /Rk £ [0, 1] there is a degree of belonging of the element to the educational process. This is a degree that shows how much the improvement of learning effectiveness depends on this element.
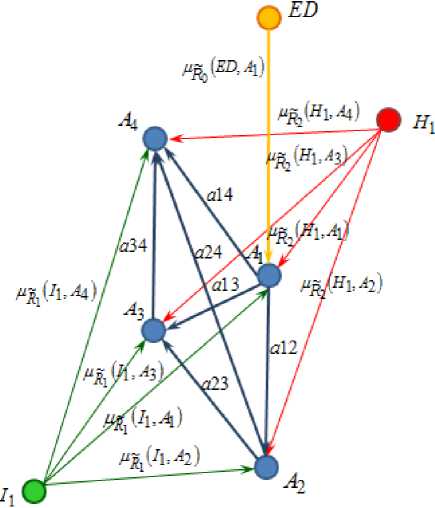
Fig. 3. The visualized information transfer model.
Investments in the learning process (set / 1 ) can be not only financial. In a broad sense, investments also represent the efforts and additional work of a teacher associated with optimizing the presentation of educational material [13]. As the pedagogical experience of the author and the observation of the educational process of other teachers shows, a more thorough study of individual topics of academic disciplines contributes to their better presentation to students. Usually, students, seeing the efforts and interest of the teacher, also get carried away with the course. There is an increase in their academic performance [14].
Interference (H 1 ) interfering with the effective transmission of educational information may be:
-
• Insufficient organizational, methodological, and technical provision of the educational process [15];
-
• Insufficient motivation of the teacher for explanations of the educational material that are understandable to the student audience. If the teacher does not know how to explain the material clearly and clearly, then students may have difficulty assimilating it. In addition, insufficient communication can lead to misunderstandings of instructions and assignments, which also complicates the learning process. [16];
-
• Differences in culture and language. International students may face difficulties in understanding and mastering the material. The teacher should take these differences into account and apply a variety of teaching methods to make the material accessible to all students;
-
• Teacher fatigue caused by multitasking, intensification of his work;
-
• Psychological barriers that form against the background of the demonstration of negative emotions and attitudes. The teacher should create a trusting and supportive atmosphere in the classroom so that students feel comfortable and can freely express their thoughts and ask questions about the discipline.
-
3.2. The Model of Perception of Information
The presented list contains the most common difficulties in the educational process. There may be other obstacles due to the specifics of the educational organization, the direction of training, academic discipline, etc.
The purpose of constructing and analyzing a cognitive model of operational perception of educational information is to determine the mechanism of perception and the influence of individual factors on the effectiveness of learning components.
For the model of information perception, the same assumptions are valid as for the model of information transmission, only they are considering by students.
The total potential of the information perception model is determining by the formula:
KAI = ((P a 3 +P a4U (P a s +PaJ)-R 2 (13)
The coefficients of mutual influence of the components can found from the system of equations:
Pa 3 = R- r 3 (A s , a 3 )©b3(a6, а . )(А5 , Аб , Аз ) - ^г ? з (Аз , A6 )
P a \ = {^)?3(a 3 ,a 4 )®r3(as,а 4 )(аз , A4 , А5 ) +W ?3 ( A6 , А4)} -Д й3(а4 , А6 )
’ PA S = ^з (А, А6 ) - K(AS, А 3 )®Й з (А5, А * )^ А з , А4 ) + ^з (А, А6)} (14)
ра6 = {^ з (а 3 ,a6)©R 3 (a 4 , а6)(а*з , а4 , А6 ) + W ? 3 (a5 , А6)} -
. -{pR 3 (A6, A 3 )®R 3 (A6, А 4 )(А6 , А3 , А4 ) + /i R 3 (A6 , А5)}
The visualized model of information perception is present in Figure 4 in the form of a fuzzy-oriented graph, the weights of the arcs, which are also the values of the corresponding membership functions.
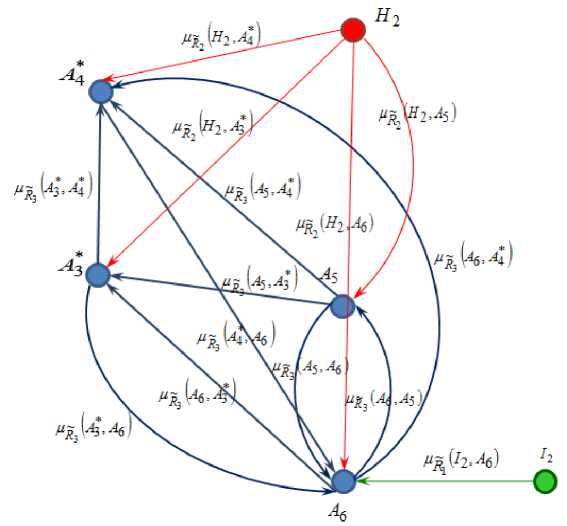
Fig. 4. The visualized model of information perception.
External factors supporting student motivation (set /2) include:
-
• Creating conditions for understanding the purpose of the activities performed by students at the level of academic assignments, at the level of mastering a specific academic discipline, passing an internship, etc.;
-
• Substantiation of the relationship between the acquired knowledge and its practical application in the future professional field. In the classroom, the teacher needs, first of all, to apply an interdisciplinary approach and establish interdisciplinary connections so that students form a knowledge system. On this basis, when studying specific topics, starting with the conceptual apparatus, the teacher needs to give examples and specifically indicate the place of the studied material in the field of the future profession [16];
-
• The use of active teaching methods in training sessions, etc.
-
3.3. The Potential of the Information Interaction Model
Hindrances to the perception of educational information (H2) lie in the psycho-behavioral types of the students themselves. It is impossible to force a person to study against his will. If students have no desire to learn, and weak internal motivation, then even the most patient and talented teacher is unlikely to immediately be able to see the positive results of their work. Often, teachers, seeing the lack of interest among students, lose it themselves. The educational process is interdependent, the art of teaching consists precisely in activating students' interest in learning through the use of active methods and technologies.
The potential of the information interaction model can be calculated as an algebraic combination of the potentials of information transmission and perception models (15) or as their average value (16).
K = K„ + KAI - KTI • KAl
К = (Kti + Kd/2
Other methods of calculating the final potential can also be used.
4. Results and Discussion 4.1. Results Of the Information Transfer Model
All experiments were carried out at 0.061 < ED < 0.238. Figure 5 shows the results of the model at 10% information transfer.
The situation numbers are indicated in column “A”, the designations in columns “B” – “J” imply the weights of the arcs of the graph shown in Figure 3. That is ill = ^^(1 1 , A 1 ), .„, i14 = ^^(1 1 , A4) , h11 = Цп2(Н 1 , A 1 ), ..., h14 = 1Лц2(Н 1 , A4). These are the input variables of the model. The output variables are the potential of the model (KTI ), the potentials of its main components (A 1 , A2, A3, A4), and the total weight of the model (Sum^a^)). The values in columns “M”- “P” are calculated using formulas (3) – (6), the potential of the model is calculated using formula (11), and the total weight of the model is the sum of the values in cells R2:W2. These coefficients, in turn, are determined from the system (12) using the MS Excel Solver service.
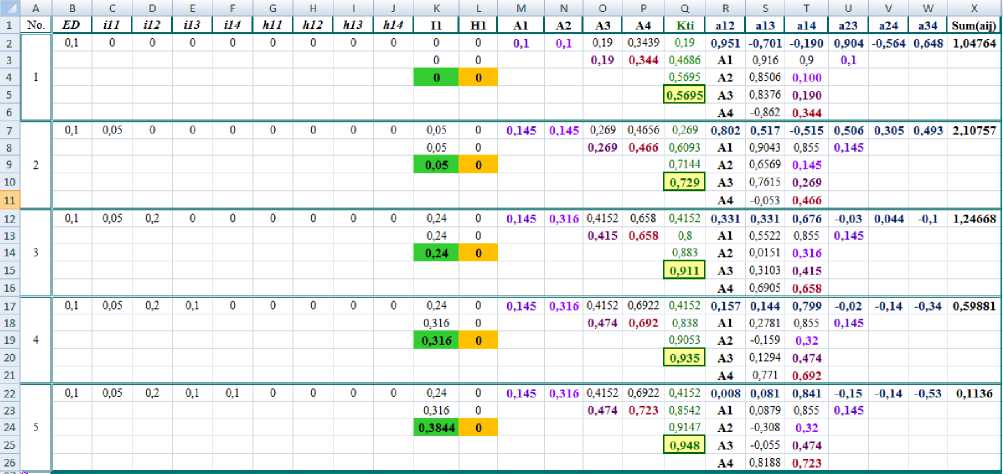
Fig. 5. The results of the work information transmission model with investing.
The coefficients a ij can range from -1.0 to +1.0. The closer they are to the boundary values, the stronger their influence in the model. The proximity of these values to zero indicates a weak influence. The signs at the coefficients can be interpreted as follows. The “+” sign indicates the predominant influence of the first element, and the “-” sign indicates the predominant influence of the second element.
As shown in Figure 5, when transmitting 10% of information without investment and interference (situation No. 1), the potential of the model is 0.5695. This value is estimated as an average. Lectures, as well as presentations and guidelines, are of the greatest importance in this situation. The gradual addition of investments helps to increase the potential of the model but also reduces its overall weight. Therefore, the investment should be within reasonable limits. Further reinforcement of such a model is not economically feasible.
When transmitting information without reinforcement, but taking into account interference, the model cannot determine the potentials of the components (A 1 , A2, A3, A4) with a noticeable decrease in potential. A further increase in the influence of interference leads to a zero potential of the model, which indicates the impossibility of its existence. However, if reinforcement is added under the influence of interference, we will get the results as shown in Figure 6.
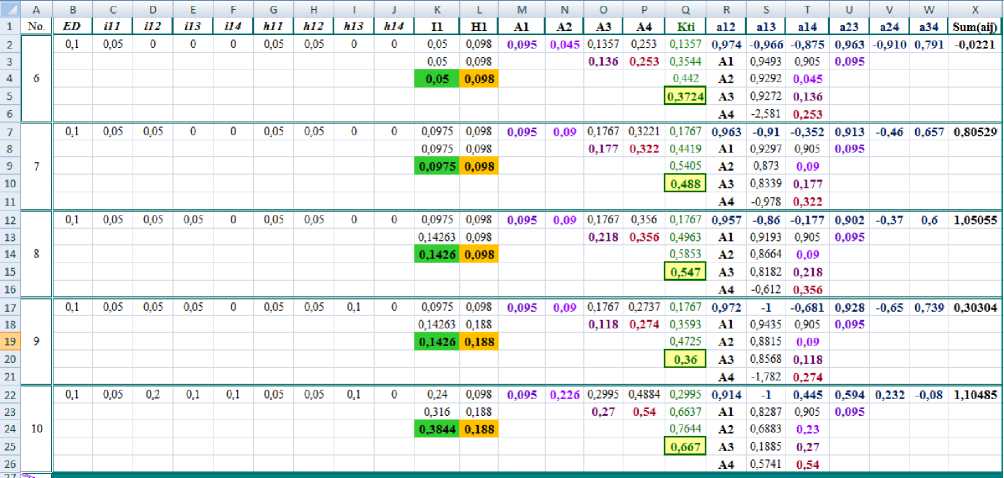
Fig. 6. The results of the information transmission model with reinforcement and interference.
Situation No. 6 shows a 5% effect of interference h 11 and h12, as well as a 5% effect of investment 1 11 . Despite the exceeding influence of interference, the potential of the model increased to 0.3724. Further increasing investments at the same level of interference impact ensures an increase in the potential and overall weight of the model. Interference of new interference (situation No. 9) reduces both the potential of the model and its total weight. However, the predominance of positive factors (situation No. 10) corrects the state of the information transmission model.
-
4.2. Results Of the Information Perception Model
The work of the information perception model is based on the same principles and assumptions as the work of the information transmission model. The input variables are B3 , ^a1(l2, A6), ^2(Н2, A 3 ), ^2(Н2, A *4 ) , ^r2(H2, A5), Br2(H2, A6). In Figures 7 and 8, the input variables are indicated respectively as B3, i26, h23, h24, h25, h26. The value of S3 is calculated by formula (5) as the sum of the potentials of components A 1 and A2. The remaining values are set by the expert. The output variables are the potential of the model (KAI ), its main components (A 3 , A 4 , A5, A6) and the total weight of the model (Sum(a ij )). The values in columns “J”-“M” in Figures 7 and 8 are calculated using formulas (7) – (10), the potential of the model is calculated using formula (13), and the total weight of the model is the sum of the values in the cells O2:W2. These coefficients, in turn, are determined from the system (14) using the MS Excel Solver service.
As shown in Figure 7, students’ perception of lectures, presentations, and methodological guidelines without additional reinforcement and any interference at the 0.19 level provides the potential of the model equal to 0.5695 (average level). The total weight of the model is 0.61168. A positive value indicates that the model is working well. In the second situation, B3 = 0.269, which provides both an increase in the potential of the model and its total weight. The following experiments confirm this trend. An attempt at a small reinforcement of the model (situation No. 4) improves the condition of the model, but exceeding the investment of more than the required volume significantly reduces the overall weight of the model. This means that the model can only be improved to a certain level.
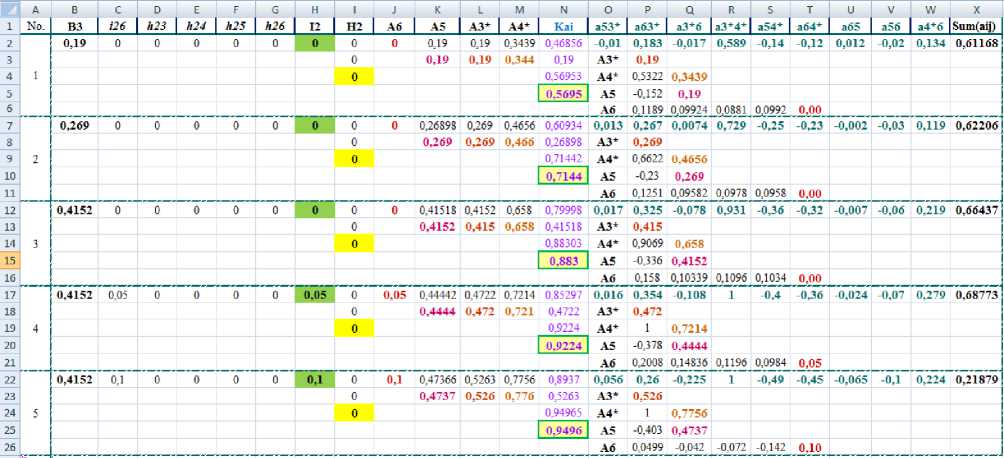
Fig. 7. The model of information perception with reinforcement.
Perception of information without reinforcement, but taking into account interference (situation No. 6) reduces the potential of the model, and its total weight makes it negative, which indicates a lack of efficiency. A further increase in the influence of interference indicates the impossibility of the model’s existence. However, if reinforcement is added under the influence of interference, we will get the results as shown in Figure 8.
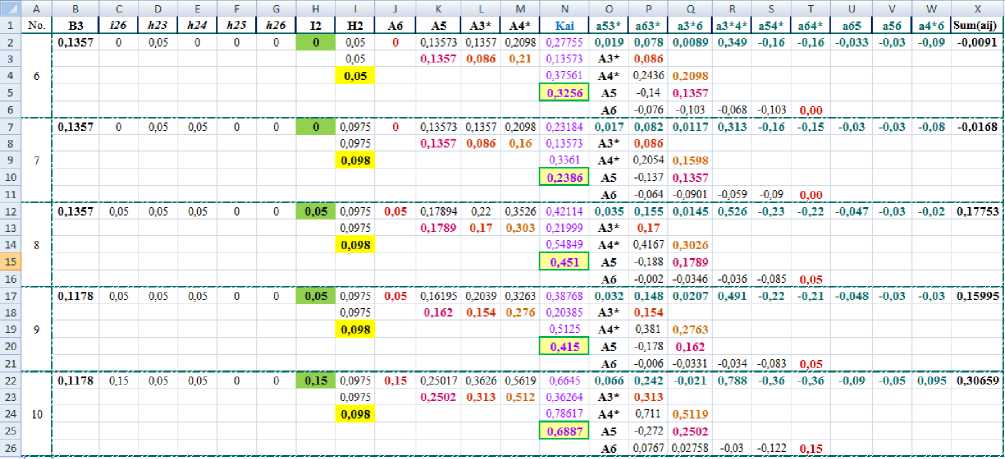
Fig. 8. The results of the information perception model with reinforcement and interference.
Situation No. 8 shows a 5% effect of interference h23 and h24, and a 5% effect of investment i26. Despite the exceeding influence of interference, the potential of the model increased to 0.451. With a decrease in the volume of perceived information, the potential of the model decreases slightly (situation No. 9), however, with an increase in the investment component (i26 = 0.15), the potential of the model increases significantly.
-
4.3. Calculation Of the Potential Of The Information Interaction Model
The table contains the initial data for calculating the potential of the information interaction model, and the last two columns present the results of the calculations. The first column of the table shows the double number of the situation. The first digit of the number indicates the number of situations shown in Figures 5 and 6. The second digit in parentheses is the number of the situations from Figures 7 and 8.
Table 1. Calculation of the Potentials of the Information Interaction Model
|
No. |
B 3 |
K ti |
Model weight TI |
km |
Model weight AI |
Potentials of the Information Interaction Model |
|
|
Formula (15) |
Formula (16) |
||||||
|
1(1) |
0.190 |
0.5695 |
1.0476 |
0.5695 |
0.6117 |
0.815 |
0.570 |
|
2(2) |
0.269 |
0.7290 |
2.1076 |
0.7144 |
0.6221 |
0.923 |
0.722 |
|
3(3) |
0.415 |
0.9110 |
1.2467 |
0.8830 |
0.6644 |
0.990 |
0.897 |
|
3(4) |
0.415 |
0.9110 |
1.2467 |
0.9224 |
0.6877 |
0.993 |
0.917 |
|
3(5) |
0.415 |
0.9110 |
1.2467 |
0.9496 |
0.2188 |
0.996 |
0.930 |
|
6(6) |
0.136 |
0.3724 |
-0.0221 |
0.3256 |
-0.0091 |
0.577 |
0.349 |
|
6(7) |
0.136 |
0.3724 |
-0.0221 |
0.2386 |
-0.0168 |
0.522 |
0.306 |
|
6(8) |
0.136 |
0.3724 |
-0.0221 |
0.4510 |
0.1775 |
0.655 |
0.412 |
|
9(9) |
0.118 |
0.3600 |
0.3030 |
0.4150 |
0.1599 |
0.626 |
0.388 |
|
9(10) |
0.118 |
0.3600 |
0.3030 |
0.6887 |
0.3066 |
0.801 |
0.524 |
As can be seen from the table, the model has the greatest potential in situation 3(5). The lowest potential is typical for the model in situation 6(7).
Situation 3(5) in the information transfer model, there is a situation with reinforcement of the teacher's activity. It provides for investing in the preparation of lectures by a teacher (1 11 = 0.05) and the preparation of presentations, and methodological recommendations (i12 = 0.2). In practice, this can be expressed in additional payment to the teacher for time to prepare lectures and presentations. For example, it takes six academic hours to transfer 10% of the educational information from the entire course. At the same time, the teacher spends an average of 2 hours preparing one lecture and 1 hour preparing a presentation (methodological recommendations). One academic hour of classroom work is paid in the amount of 405 monetary units, a total of 2 430 monetary units. The additional payment for the preparation of one lecture will be 405*2 *0.05 +405*0.20 = 40.5+81 = 121.5 monetary units. There are three such lectures, which means that in addition to the basic salary, the teacher will receive 364.5 monetary units. The effect of interference in this situation is not considered.
In the information perception model, situation 3(5) is also a situation without interference, but with 10% reinforcement. The practice-oriented nature of the educational material can act as an incentive for students. The information provided to students can be very useful in their work.
Situation 6(7) has interference in both models. At the same time, there is no reinforcement in the information perception model. As a result, this situation is recognized as the most inefficient.
-
4.4. Comparative Analysis of the Actual and Model Results of Interaction in the Educational Process
All the models presented above are based on the results of classroom work by teachers and students in the economic field. Table 2 shows the results of the transfer of information, actual and obtained by the model. The fact values KTI (fact) are determined by how many units of educational information the teacher was able to transfer in one lesson according to the established plan.
Table 2. Actual and Model Results of the Transfer of Educational Information
|
No. |
I I |
H l |
K TI (fact) |
K TI (calcul.) |
Approximation error |
|
1 |
0.000 |
0.000 |
0.6 |
0.5695 |
0.0508 |
|
2 |
0.050 |
0.000 |
0.7 |
0.7290 |
0.0414 |
|
3 |
0.240 |
0.000 |
0.9 |
0.9110 |
0.0122 |
|
4 |
0.316 |
0.000 |
0.9 |
0.9350 |
0.0389 |
|
5 |
0.384 |
0.000 |
0.9 |
0.9480 |
0.0533 |
|
6 |
0.050 |
0.098 |
0.4 |
0.3724 |
0.0690 |
|
7 |
0.098 |
0.098 |
0.5 |
0.4880 |
0.0240 |
|
8 |
0.143 |
0.098 |
0.5 |
0.5470 |
0.0940 |
|
9 |
0.143 |
0.188 |
0.4 |
0.3600 |
0.1000 |
|
10 |
0.384 |
0.188 |
0.7 |
0.6670 |
0.0471 |
The main element of theory and an example of its practical use are accepted as a unit of educational information. For example, the optimal plan is ten basis units. The teacher, without additional reinforcement, transmits six basic units to the student audience, and then the actual value of the potential of the information transfer model is 0.6. This does not mean that the lesson plan is not being implemented, but only indicates that the plan could have been performed better. For example, a teacher could enhance the transmission of information with additional practical examples.
The average approximation error of the model values is 0.053 or 5.3% and does not exceed 7%, which indicates the good quality of the model.
Table 3 shows the results of the information perception model in comparison with the actual data. The fact values are the proportion of the material learned by students on average in the group. For example, of the ten pieces of information transmitted by the teacher, an average of seven units were mastered. The actual value will be 0.7. The values are revealed by testing students.
Table 3. Actual and Model Results of Perception of Educational Information
|
No. |
в 3 |
^ 2 |
^ 2 |
В та (fact) |
К ТА (calcul.) |
Approximation error |
|
1 |
0.190 |
0.00 |
0.00 |
0.6 |
0.5695 |
0.0508 |
|
2 |
0.269 |
0.00 |
0.00 |
0.7 |
0.7144 |
0.0206 |
|
3 |
0.415 |
0.00 |
0.00 |
0.8 |
0.8830 |
0.1038 |
|
4 |
0.415 |
0.05 |
0.00 |
0.9 |
0.9224 |
0.0249 |
|
5 |
0.415 |
0.10 |
0.00 |
0.9 |
0.9496 |
0.0551 |
|
6 |
0.136 |
0.00 |
0.05 |
0.3 |
0.3256 |
0.0853 |
|
7 |
0.136 |
0.00 |
0.10 |
0.2 |
0.2386 |
0.1930 |
|
8 |
0.136 |
0.05 |
0.10 |
0.5 |
0.4510 |
0.0980 |
|
9 |
0.118 |
0.05 |
0.10 |
0.4 |
0.4150 |
0.0375 |
|
10 |
0.118 |
0.15 |
0.10 |
0.7 |
0.6887 |
0.0161 |
The comparison of the actual and calculated values was also carried out using the average approximation error, which is 0.0685 or 6.85%. It is also less than 7%, which indicates the good quality of the model.
The values of information interaction in the situations discussed in Table 1, calculated based on the results of transmission and perception of educational information, are shown in Table 4.
Table 4. Comparison of the Potentials of the Information Interaction Model and Potentials of Classroom Information Interaction
|
No. |
Potentials of the Information Interaction Model |
Potentials of Classroom Information Interaction |
Approximation error |
|||
|
Formula (15) |
Formula (16) |
Formula (15) |
Formula (16) |
Formula (15) |
Formula (16) |
|
|
1(1) |
0.815 |
0.570 |
0.840 |
0.600 |
0.0301 |
0.0508 |
|
2(2) |
0.923 |
0.722 |
0.910 |
0.700 |
0.0138 |
0.0310 |
|
3(3) |
0.990 |
0.897 |
0.980 |
0.850 |
0.0098 |
0.0553 |
|
3(4) |
0.993 |
0.917 |
0.990 |
0.900 |
0.0031 |
0.0186 |
|
3(5) |
0.996 |
0.930 |
0.990 |
0.900 |
0.0056 |
0.0337 |
|
6(6) |
0.577 |
0.349 |
0.580 |
0.350 |
0.0056 |
0.0029 |
|
6(7) |
0.522 |
0.306 |
0.520 |
0.300 |
0.0041 |
0.0183 |
|
6(8) |
0.655 |
0.412 |
0.700 |
0.450 |
0.0636 |
0.0851 |
|
9(9) |
0.626 |
0.388 |
0.640 |
0.400 |
0.0225 |
0.0313 |
|
9(10) |
0.801 |
0.524 |
0.820 |
0.700 |
0.0235 |
0.2509 |
The approximation error of the values determined by the formula (15) was 0.018 (1.8%). The calculation using the formula (16) showed an error of 5.8%. Both results are acceptable and confirm the good quality of the information interaction model.
5. Conclusion
As a result of the research, a model of information interaction between a teacher and students has been created, based on the joint use of an information transmission model and an information perception model. The teacher plays an active role in the information transfer model. Students play an active role in the information perception model. The model of information interaction between teachers and students is designed to develop recommendations for improving the effectiveness of the educational process. The effectiveness of the educational process is understood as matching the costs and efforts of both the teacher and the students to the result. The result here is the percentage of students mastering educational information. The study found that the more benevolent the teacher and students are towards each other, the more effective the learning process. An additional incentive may be investments in the educational process, and not only of a financial nature.
The method that has shown good effectiveness in practice is the introduction of modern information technologies into the educational process, which are well understood by both the teacher and the students. The use of digital services increases the interest of the student audience in the educational process. Accordingly, the level of mastering educational information, academic performance, and the effectiveness of the educational process as a whole increases.
The developed model of information interaction can be used by teachers of various academic disciplines to identify the advantages and disadvantages of the educational process. Based on the simulation results, teachers can conclude about the effectiveness or insufficient effectiveness of the educational process and offer management (for example, the head of the department or the dean of the faculty) a joint solution to the identified problems.
Future research suggests the development of educational strategies for teachers, taking into account the perception of learning information by student groups.
Список литературы Modeling Interaction in the Educational Process is a Tool for Improving its Effectiveness
- Jacek Uziak, Edmund Lorencowicz, Milan Koszel, Sławomir Kocira, The Information Technology Use and Skillsby Undergraduate Students: Case Study. Edukacja - Technika - Informatyka, 4(26), 163−168, 2018. DOI: 10.15584/eti.2018.4.22
- F.K. Urakova, I.I. Ishmuradova, N.A. Kondakchian, R.S. Akhmadieva, J.V. Torkunova, I.N. Meshkova, N.A. Mashkin, Investigating Digital Skills among Russian Higher Education Students. Contemporary Educational Technology, 15(1), ep398, 2023. https://doi.org/10.30935/cedtech/12600
- B.T. Sampath Kumar, S.U. Shiva Kumara, The Digital Divide among the Rural and Urban Students: An Exploration. South Asian Journal of Participative Development, 18(2), 160−167, 2018.
- Arsad Bahri, Asham Bin Jamaluddin, Arifah Novia Arifin, Saparuddin, Students’ and Teachers’ Digital Literacy Skill: A Comparative Study between Schools, Classes, and Genders in Urban and Rural Areas. International Journal of Science and Research (IJSR), 11(2), 184–191, 2022. DOI: 10.21275/SR22130101519
- I.V. Tsvetkova, O.A. Bezgina, O.S. Evchenko, V.A. Gurov, S.Yu. Vasileva, Problems of Informatization of Higher School in the Perception of Subjects of the Educational Process. SHS Web Conf. 121 03008, 2021. DOI: 10.1051/shsconf/202112103008
- D.A. Lisachenko, A.V. Barmasov, M.N. Bukina, E.N. Stankova, S.O. Vysotskaya, E.P. Zarochentseva, Best Practices Combining Traditional and Digital Technologies in Education. In: Gervasi, O., et al. Computational Science and Its Applications – ICCSA 2017. ICCSA 2017. Lecture Notes in Computer Science, vol. 10408. Springer, Cham. 2017. https://doi.org/10.1007/978-3-319-62404-4_36
- Jamilurahman Faizi, Mohammad Sarosh Umar, A Conceptual Framework for Software Engineering Education: Project Based Learning Approach Integrated with Industrial Collaboration. International Journal of Education and Management Engineering, 11(5), 46–53, 2021.
- Phyo Thu Thu Khine, Htwe Pa Pa Win, Tun Min Naing, Towards Implementation of Blended Teaching Approaches for Higher Education in Myanmar. International Journal of Education and Management Engineering, 11(1), 19–27, 2021.
- Naimuddin Ansary, Traditional and Digital Resources in the Teaching Learning Process: Advantages and Limitations. FORTELL, 45, 174–185, 2022. URL: https://www.fortell.org/wp-content/uploads/2022/10/July-2022-174-185.pdf (date of application: 12.04.2024)
- I.V. Drobysheva, Yu.A. Drobyshev, Digital Economy Competencies: Experience and Stages of Formation among University Students. Bulletin of the Peoples’ Friendship University of Russia. Series: Informatization of education, 20(3), 255–264, 2023. DOI: https://doi.org/10.22363/2312-8631-2023-20-3
- Mohammed Abdullah Al-Hagery, Maryam Abdullah Alzaid, Tahani Soud Alharbi, Moody Abdulrahman Alhanaya, Data Mining Methods for Detecting the Most Significant Factors Affecting Students’ Performance. International Journal of Information Technology and Computer Science, 12(5), 1–13, 2020.
- I.N. Odarich, T.G. Sobakina, S.A. Gorovoy, Organization Methodological Support of the Educational Process in Higher Education. Revista on line de Política e Gestão Educacional, Araraquara, 25(2), 863−871, May 2021. e-ISSN:1519-9029. DOI: https://doi.org/10.22633/rpge.v25iesp.2.15272
- E.A. Nikitina, Formation of Leadership Qualities of a Future Teacher in the Educational Process of a Higher Educational Institution. Russian Research and Practice Journal of Studies in Social Sciences and Humanities, 3(10), 9–16, 2023.
- Mesta Limbong, Analysis of Obstacles and Difficulties in the Process of Implementing Learning for Students Based on the Learning Management System (LMS). International Journal of Educational Management and Innovation, 4(2), 115–126, May 2023.
- A.A. Osipova, L.A. Dyatlova, E.N. Ryadinskaya, M.A. Luk’yanenko, Psychological and Pedagogical Technologies for Overcoming Meaning Barriers in the Learning Process. Russian Psychological Journal, 15(2), 260–278, 2018 (in Russian).
- E.J. Kistnasamy, The Power of Extrinsic Motivation in Tertiary Education. American Journal of Educational Research, 2(6), 383–388, 2014. DOI:10.12691/education-2-6-9


