Modeling of oil reservoirs heat losses by nanodimensional cellular automata

Modeling of oil reservoirs heat losses by nanodimensional cellular au-tomata by Baikov I.R. , Smorodova O.V. , Kitaev S. V., Kuznetsova E.V. , Gizatullina D.T. is licensed under a Creative Commons Attribution 4.0 International License.
Based on a work at a>.
Permissions beyond the scope of this license may be available at .

Modeling of oil reservoirs heat losses by nanodimensional cellular au-tomata by Baikov I.R. , Smorodova O.V. , Kitaev S. V., Kuznetsova E.V. , Gizatullina D.T. is licensed under a Creative Commons Attribution 4.0 International License.
Based on a work at a>.
Permissions beyond the scope of this license may be available at .

В настоящее время для хранения нефти и нефтепродуктов широко используются стальные цилиндрические вертикальные резервуары, которые являются важнейшей и неотъемлемой частью нефте-парков страны [1, 2]. Высокая испаряемость нефти и нефтепродуктов приводит к их значительным потерям при хранении [3, 4].

В процессе испарения нефти часть легких углеводородов переходит в газообразное состояние, в результате чего происходит естественная массовая убыль продукта. Нормами предусмотрено лишь количественное изменение, тогда как при испарении изменяется и качественный состав хранимой нефти. При естественных температурах перекачки и перевалки при испарении в первую очередь теряются легкие углеводороды фракции 200 (до гексанов включительно), являющиеся компонентами автомобильных бензинов. Это снижает качество нефти по «дистилляционной» модели, учитывающей наличие в нефти светлых фракций [5].

Интенсивность испарения нефти кроме технологического режима с изменением уровня взлива резервуара [6] определяется ее температурой. В условиях российского севера при работе с высоковязкой нефтью технологические резервуары жидкости и нефти оснащены тепловой изоляцией [7]. В качестве теплоизоляционного материала наиболее широко используются минеральная вата (МВ), пенополиуретан (ППУ), каменная вата (КВ). Следует отметить, что теплозащитные свойства названных материалов на первоначальном этапе эксплуатации находятся на сопоставимом уровне (рис. 1а). Практический выбор определяется прочими тех- нологическими свойствами тепловой изоляции – надежностью, долговечностью, горючестью и пр. В частности, наиболее распространенная минеральная вата обладает худшими из всех названных материалов теплозащитными свойствами (рис. 1а) и недостаточной износостойкостью из-за повышенной сминаемости (рис. 1б).

Пенополиуретан, несмотря на широкое применение на объектах магистрального транспорта нефти для инженерных коммуникаций, обладает некоторой горючестью (группа Г2, Г3 по ГОСТ 12.1.044-89 «Взрывопожароопасность веществ и материалов»), и потому не может быть рекомендован без ущерба надежности и безопасности резервуарных парков углеводородов. Оптимальной тепловой изоляцией для опасных производственных объектов является каменная вата (КВ-тепловая изоляция).

ОСНОВНАЯ ЧАСТЬ

Построение одномерной модели теплопроводности методом клеточных автоматов

Практическое управление тепловым режимом нефтяного резервуара возможно на основе моделирования температурных условий по результатам мониторинга термодинамических показателей нефти и ограждающих конструкций резервуаров. В статье рассмотрена задача моделирования распределения температур в поперечном срезе наружных ограждений нефтяных резервуаров. Решение выполнено на основе эксплуатационных технологических данных резервуарных парков северных месторождений России. Расчеты при разработке температурных моделей проведены для КВ-тепловой изоляции.

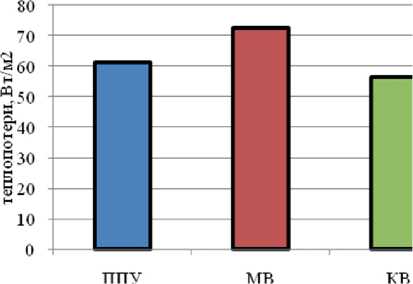
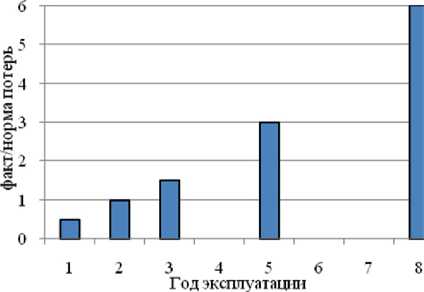
б - интенсивность старения МВ- изоляции

a - плотность теплового потока теплопотерь

Рис. 1. Характеристики материалов для тепловой изоляции резервуаров нефти

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

Авторами работ [8, 9, 10, 11, 12] для симуляции теплопроводности в ограждающих стенках технологических сооружений рекомендуется метод клеточного автомата. В последних работах [13, 14] с помощью КА-моделирования симулируются биологические, физические, информационные процессы. Такой подход особенно продуктивен в том случае, когда классические модели представляют собой многофакторные дифференциальные структуры [15].

Основой клеточно-автоматного моделирования служит дискретная модель – регулярная решетка ячеек, для каждой из которых определено конечное множество состояний [16]. Для каждой клетки определена клеточная окрестность. При этом задаются начальные состояния всех ячеек и правила их смены. Такой метод позволяет исследовать локальные механизмы моделируемой системы на наноуровне [17].

Реализация КА-моделирования проведена для резервуаров самых распространенных типоразмеров – 5000 м3, 10000 м3 и 20000 м3. Величина отношения толщины стенки резервуаров к диаметру на уровне от 0,0005 до 0,0009 м/м позволяет вести моделирование в формате плоской задачи. Для имитирования температурного поведения в поперечном срезе наружных ограждений в качестве локальных элементов были выделены наноразмерные ячейки дискретного температурного состояния [18]. В этом случае каждая ячейка-клетка представляет собой микроэлемент материала – «крупнозернистое» вещество.

Согласно теории конечных автоматов [19], состояние отдельной клетки на каждом шаге по времени изменяется в соответствии с функцией переходов:

z(t _j ) = ϕ [z(t _j–1 ), X (t _j–1 )], (1)

где z(t _j ) – состояние клетки в момент времени t _j ;

X(t _j–1 ) – вектор входных сигналов в предыдущий момент.

Рассмотрим одномерную задачу теплопроводности, где в качестве объекта будет выступать многослойное наружное ограждение нефтяного резервуара, на левой границе которого в начальный момент времени локализован тепловой импульс [20]. Разобьем ограждающую поверхность на элементы (клетки) с одинаковым шагом h и отождествим состояние клетки с ее температурой Т. Входные сигналы моделируют процесс передачи тепловой энергии от соседних клеток и от источника теплоты. Для рассматриваемого случая одношаговая функция переходов i-й клетки запишется так [21]:

T _i (t _j+1 ) = T _i (t _j )+(∆t/C•ρ)•[q _i-1 (t _j )+q _i+1 (t _j )+γ(t _j )], (2)

(T i–1 (t j )–T i (t j ) q _i–1 = λ       _h2

(T _i+1 (t _j )–T _i (t _j ) q _i+1 = λ       _{h 2}

где T _i (t _j ) – температура i-й клетки в момент времени t;

j

∆t – шаг по времени;

C, λ и ρ – теплоемкость, коэффициент теплопроводности и плотность материала клетки, соответственно;

q _i–1 (t _j ) и q _i +1(t _j ) – удельные мощности тепловых потоков от соседних клеток;

γ(t _j ) – удельная мощность источника теплоты в j-й момент времени.

Процесс моделирования сводится к определению состояний клеточных автоматов на каждом шаге дискретного времени [22]. При этом каждый автомат функционирует по определенному алгоритму. Для внутренних клеток стенки резервуара используется функция переходов вида (2)–(3). Для внешних границ тепловой изоляции данные зависимости

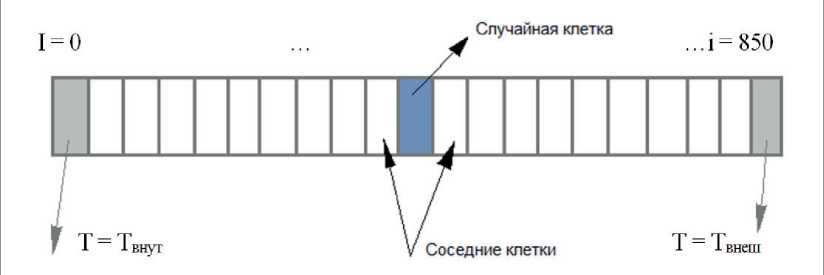
Рис. 2. Клеточная структура ограждающей стенки резервуара

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ модифицированы, исходя из гипотезы о нулевом градиенте температуры в данных точках (равенство тепловых потоков от соседних клеток).

В условиях практической реализации одномерное моделирование на основе клеточных автоматов представляет собой последовательность итерационных клеточно-автоматных взаимодействий асинхронного типа. Каждый итерационный цикл предусматривает реализацию следующих процедур:

• 1.    На КА-поле случайным образом идентифицируется некоторая клетка і = 1 с координатой x1. Все ячейки имеют одинаковую вероятность идентификации.

• 2.    Соседняя клетка і = 2 с координатой x2 выбирается случайным образом по схеме соседства из окрестности Неймана (у клетки есть только два соседа, рис. 2).

• 3.    Реализуется КА-взаимодействие между выбранными клетками. Смысл взаимодействий заключается в пересчете значений температуры теплоизоляционного материала резервуара в клетках поля моделирования по уравнениям (2)–(3), которые представляют собой клеточно-автоматный аналог процесса теплопроводности [9].

В простейшем случае стационарной теплопроводности одношаговая функция переходов i-й клетки рассчитывается по формуле:

Tij+1 = λiTij+ λi+1Tji+1/ λi+ λi+1, где j+1 – номер итерации;

T _i ^j+1 – новая установившаяся температура в случайной клетке;

T _i ^j – первоначальное значение температуры в этой же клетке;

• λ _i – коэффициент теплопроводности материала в данной клетке;

T^j _i+1 – температура одной из случайно выбранных соседних ячеек;

• λ _i+1 – коэффициент теплопроводности материала выбранной соседней ячейки.

В применении к частному случаю моделирования температурного графика в стенке резервуара задача формулируется так. Нефтяной резервуар покрыт тепловой изоляцией из минеральной ваты базальтового волокна – каменной ваты. С внутренней стороны на стенках резервуара образован слой парафинистых отложений. Основные характеристики ограждений резервуара приведены в табл. 1.

Результаты моделирования одномерного поля, содержащего 850 ячеек, в пределах погрешности клеточно-автоматного «шума» приведены на рис. 3.

Оптимизация клеточно-автоматного моделирования

Очевидно, что для обеспечения адекватности результатов моделирования реальному процессу размерность модельного поля следует принимать, возможно, большей. Однако это неизбежно увеличит продолжительность моделирования даже при использовании современного быстродействующего вычислительного оборудования [9, 11].

Для оценки степени влияния количества клеток автомата на результат моделирования температуры были выполнены построения модели для трех случаев размерности поля. На основе предварительно проведенных вычислительных экспериментов было отобрано 17, 85 и 850 клеточных автоматов по толщине слоя. В качестве слоя был взят слой именно тепловой изоляции, т.к. в металлической стенке резервуара температура изменяется незначительно и ее динамика не представляет практического интереса. Результаты моделирования показаны на рис. 4.

Абсолютные отклонения модельной температуры от вычисленной аналитически приведены на рис. 5.

Оценка качества построенной модели была проведена по величине среднеквадратического отклонения модельной температуры от аналитически рассчитанной (рис. 6).

Таблица 1

Технические характеристики наружных ограждений резервуара

№	Наименование слоя	Толщина	Коэффициент теплопроводности	Количество ячеек
		мм	Вт/(м2К)	шт
1	Отложения	1	0,4	10
2	Стальной лист	24	52,0	240
3	Тепловая КВ-изоляция	60	0,032	600
	ВСЕГО	85		850

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

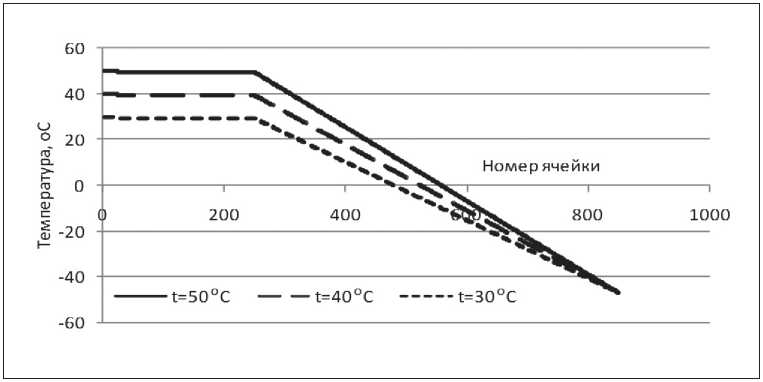
Рис. 3. Модельные температурные линии для трех тепловых режимов резервуара: t_вн = 30^оС, t_вн = 40^оС, t_вн = 50^оС

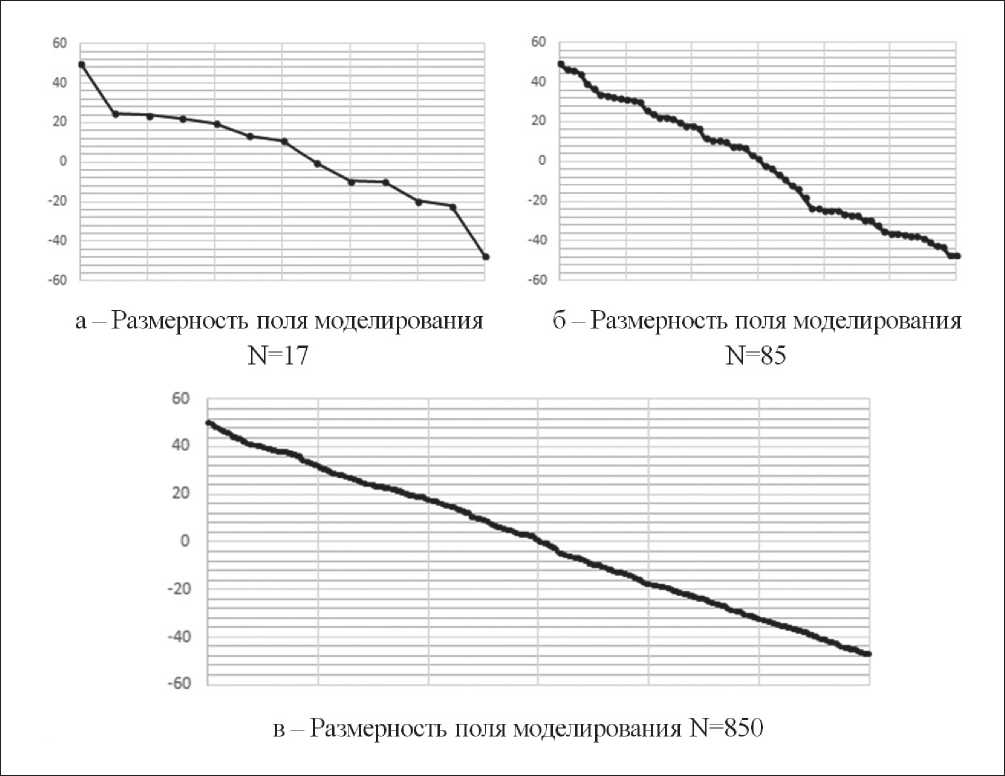
Рис. 4. Результаты моделирования распределения температур по толщине тепловой изоляции резервуара в зависимости от количества КА, ^оС

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

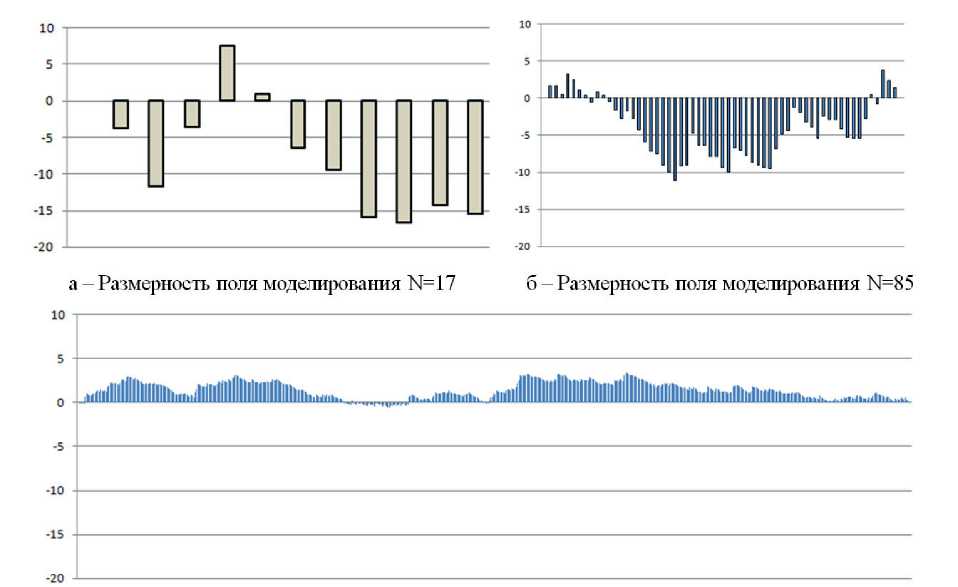
в - Размерность поля моделирования N=850

Рис. 5. Разница модельной и аналитически определенной температуры по толщине тепловой изоляции резервуара в зависимости от количества КА, ^оС

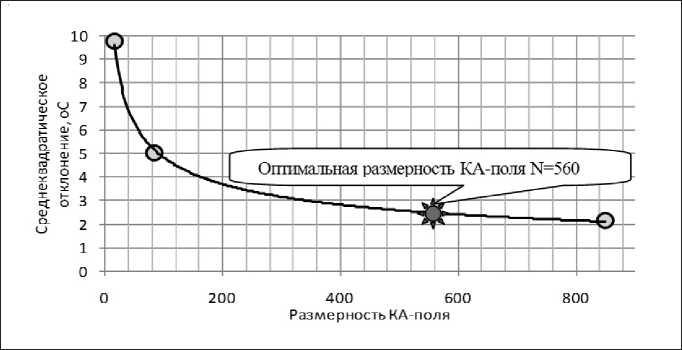
Рис. 6. Зависимость точности моделирования от размерности КА-поля

Результаты моделирования показали, что в рассматриваемой задаче среднеквадратическое отклонение σ связано с размерностью клеточно-автоматного поля N степенной зависимости вида

σ = 28,75×N–0,386. (4)

Выбор необходимой и достаточной размерности поля клеточных автоматов является основным этапом при моделировании. Назначение размерности поля на оптимальном уровне позволяет минимизировать временные затраты с одновременным достижением требуемой точности результатов.

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

Из рис. 6 видно, что при увеличении размерности КА-поля среднеквадратическая ошибка моделирования температур монотонно снижается. Однако сопутствующее наращивание количества пар сравнения в структуре КА приводит к значительному увеличению времени моделирования и, как следствие, снижению оперативности получения результатов. Это является существенным недостатком в условиях производственного мониторинга режима эксплуатации промыслового оборудования.

Оптимальное решение следует принимать с учетом точности используемых приборов для контроля температур среды в резервуаре и на поверхности изоляционного слоя. Как правило, для измерения температур в диапазоне (–100; +100)oС используются хромель-копелевые (ХК) термопары. В этом интервале температур допустимая абсолютная погрешность инструментального контроля составляет ±2,5oС.

С помощью уравнения (4) было установлено, что для обеспечения такой точности достаточной является размерность КА-поля с количеством ячеек моделирования N = 560 (рис. 6).

ЗАКЛЮЧЕНИЕ

• 1.    Рассмотрен альтернативный численный метод решения задач теплопроводности. Получено распределение температур в наружном изоляционном слое резервуара в условиях Крайнего севера России методом КА-моделирования. Показано, что среднеквадратическое отклонение модели 1,7^oС обеспечивается размерностью КА-поля на уровне N = 850 ячеек.

• 2.    Проведение виртуального эксперимента по моделированию теплопроводности в изоляционном слое позволило идентифицировать степенную зависимость точности моделирования от размерности КА-поля для нефтяных резервуаров парков центральных пунктов сбора северных месторождений. Установлено, что полученная зависимость характеризуется дисперсией адекватности на уровне 0,99.

• 3.    Показано, что для КА-моделирования при производственном мониторинге режимов эксплуатации резервуарных парков нефти оптимальным с точки зрения точности и оперативности получения результатов является размерность КА-поля N = 560 ячеек.