Modeling Uncertainty in Ontologies using Rough Set

Published Online April 2016 in MECS

Modelling uncertainty in ontologies has become a concern to ontologies builders, especially in the WWW community. The need of modelling and reasoning with uncertainty has been found in many different Semantic Web contexts such as matchmaking in Web services, classification of genes in bioinformatics, multimedia annotation and ontology learning [3]. In their effort to handle uncertainty in the web, the W3C founded the Uncertainty Reasoning for the World Wide Web Incubator Group. In their final report, they presented requirements for better defining the challenge of reasoning with and representing the uncertain information available through the WWW and related WWW technologies[4]. This paper presents an approach of representing and interpreting uncertainty in DL ontologies based on Pawlak rough set[5]. Rough set is a mathematical tool for processing information with uncertainty and vagueness and is also a useful soft computing tool in intelligence computing[6]. Rough set has been proposed for a variety of computational applications, especially machine learning, knowledge discovery, data mining, expert systems, approximate reasoning, and pattern recognition [7][8][9][10] [11] [12]. More specifically, this paper shows that by classifying the set of attributes of an ontology into the set of crisp attributes and the set of vague attributes, and also classifies the set of relations of the same ontology into the set of crisp and vague relations, one can easily detect the uncertain aspect of the ontology and approximate them using rough set. The rest of this paper is organized as follow: in the next section, the basic notions of description logics as ontologies language and rough set are reviewed. Section 3 presents our approach for representing uncertainty in ontologies. In section 4, the instantiation of vague concepts and vague relations is defined. section 5 discusses some issues related to the representation of uncertainty in an expressive description logic. Section 6 presents some related work and finally, section 7 concludes the paper

• II.    Preliminaries

In this section, we present the basic notion of description logics and establish the connection between DL and the web ontology language (OWL) as DL constitutes the formal logic of OWL DL. We also present an overview of rough set as defined by Pawlak

• A.    Description Logics

Description logics are a family of knowledge representation formalisms which can be used to represent the terminological knowledge of an application domain in a structured and formally well-understood way. Well understood means that there is no ambiguity in interpreting the meaning of terminologies by both humans and machines. They are characterized by the use of various constructors to build complex concepts from simpler ones, an emphasis on the decidability of key reasoning tasks and by the provision of sound, complete and (empirically) tractable reasoning services[13]. Inference capability of DL makes it possible to use logical deduction to infer additional information from the facts stated explicitly in an ontology[14].

DL are made up of the following components: Instances of objects that denote singular entities in our domain of interest, Concepts which are collections or kinds of things, Attributes which describe the aspects, properties, features, characteristics, or parameters that objects can have and Relations which describe the ways in which concepts and individuals can be related to one another. It is customary to separate them into three groups:  Assertional (ABox) axioms, Terminological

(TBox) axioms and Relational (RBox) axioms.

• •    ABox axioms capture knowledge about named individuals. For example, Father(peter) is a concepts assertion which asserts that peter is an instance of the concept Father . hasChild(Peter, Amina) is a role

assertion which asserts that Peter is the parent of Amina.

• •    TBox axioms describe relationships between concepts. For example, the general concept inclusion such as Mother C Parent which defines Mother as subsumed by the concept Parent. Fig.1 defined in Baader & Werner [15] shows a sample Tbox describing the family relationship.

MotherWithoutDaughter= Mother n V hasChild. ' Woman

• •    RBox axioms refer to properties of roles. It captures interdependencies between the roles of the considered knowledge base. For example the role inclusion motherOf C parentOf.

An ontology is said to be satisfiable if an interpretation exists that satisfies all its axioms. When an ontology is not satisfied in any interpretation, it is said to be unsatisfiable or inconsistent.

An interpretation I = (∆ ^I , . ^I ) consists of a set ∆ ^I called the domain of I , and an interpretation function ^.I that maps each atomic concept A to a set A I с A I , every role R to a binary relation R I , subset of ^A I x ^A I and each individual name a to an element a ^I ∈ ∆ ^I .

There exist several DL and they are classified based on the types of constructors and axioms that they allow, which are often a subset of the constructors in SROIQ. The description logic ALC is the fragment of SROIQ that allows no RBox axioms and only n, LI, -, 3 and V as its concept constructors. The extension of ALC to include transitively closed primitive roles is traditionally denoted by the letter S. This basic DL is extended in several ways. Some other letters used in DL names hint at a particular constructor, such as inverse roles I, nominals O (i.e., concepts having exactly one instance), qualified number restrictions Q, and role hierarchies H. For example, the DL named SHIQ is obtained from S by allowing additionally the role hierarchies, inverse roles and qualified number restrictions. The letter R most commonly refers to the presence of role inclusions, local reflexivity Self, and the universal role U, as well as the additional role characteristics of transitivity, symmetry, asymmetry, role disjointness, reflexivity, and irreflexivity[14].

Although DL have a range of applications, OWL is one of its main applications. OWL is based on Description Logics but also features additional types of extra-logical information such as ontology versioning information and annotations. Rudolph16. The main building blocks of OWL are indeed very similar to those of DL, with the main difference that concepts are called classes and roles are called properties[14]. Large parts of OWL DL can indeed be considered as a syntactic variant of SROIQ. In many cases, it is indeed enough to translate an operator symbol of SROIQ into the corresponding operator name in OWL.

• B.    Rough Set

Pawlak [5] defined rough set in the following way: Suppose we are given a set of objects U called the universe and an indiscernibility relation R ^ U x U representing our lack of knowledge about elements of U . Assume that R is an equivalence relation. Let X be a subset of U. We want to characterize the set X with respect to R .

• •    R - lower approximation of X is defined by

R * ( x )=|J { R ( x ) : R ( x ) c X }            (1)

x e U

In other words, The lower approximation of a set X with respect to R is the set of all objects, which can be for certain classified as X with respect to R (are certainly X with respect to R ).

• •    R - upper approximation of X is defined by

R * ( x )=|J { R ( x ) : R ( x ) n X ^ 0 }        (2)

x e U

In other words, The upper approximation of a set X with respect to R is the set of all objects which can be possibly classified as X with respect to R (are possibly X in view of R).

• •    R - boundary region of X is defined by

RN R ( X ) = R * ( X ) - R * ( X )            (3)

In other words, the boundary region of a set X with respect to R is the set of all objects, which can be classified neither as X nor as not-X with respect to R.

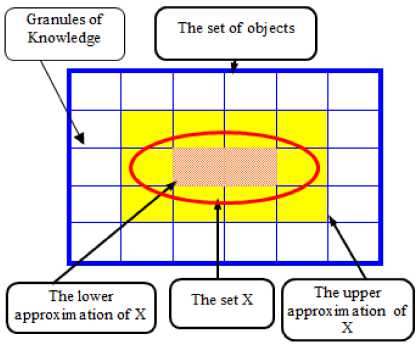
Fig.2. Rough Set Structure

A Set is rough (imprecise) if it has nonempty boundary region; otherwise the set is crisp (precise). Fig. 2 defined in Pawlak[17] shows the structure of a rough set.

• III.    Modeling Uncertainty in Ontologies

In this section, we provide a formal definition of ontology and then present our approach of modelling uncertainty in ontologies which is able to handle both crisp and the vague aspect of the world domain. In this technique, there is a clear separation between the modelling language and the representation of uncertainty itself. Such separation is useful in generalising the representation of uncertainty in ontologies regardless of the modelling language. It is also useful in reengineering existing ontologies in order to enable them to cope with uncertainty with minimal change. More importantly, without modifying the core knowledge base of ontologies.

Definition 1: An ontology system is a 6-tuple O = (D, C, R, A, I, ∑) where ≅ ⋃ , ∈ is the domain of discourse of the ontology, = {  ,  ,…,   } is a non empty finite set of concepts of domain D,

• = { _{, ,},   _,. . . ,   } is a finite set of relations,

= {  ,   ,,   ,…,   } is a finite set of attributes,

= { , ,,  ,. . . ,   } is a finite set of instances and ∑ is the chosen ontology language.

Real world is made up of crisp elements and imprecise elements. Imprecise here represents our lack of having a full knowledge of objects. It is intended to cover a variety of forms of incomplete knowledge, including incompleteness, vagueness, ambiguity, and others. Elements in this context refer to either attributes, which describes the properties of objects or relations that link individuals. Both attributes and relations can either be vague or crisp. During the conceptualization, the definition of concepts is performed by using attributes, roles and already defined concepts. Since roles and attributes are either crisp or imprecise, the obtained concepts will also be crisp or imprecise depending on the types of attributes and relations used in their conceptualization.

To express the degree of knowledge of the domain, we introduce the concept of Properties Box (PBox) as part of the ontologies knowledge base and also extend the RBox to contain more information about roles instead of performing only role declaration. PBox and the extended RBox express necessary knowledge about the properties and relationships between individuals of the domain of discourse respectively. To achieve that, the PBox classifies the attributes into the crisps attributes and vague attributes such that, the set of attributes =    ∪ where and represent the set of crisp and the set of vague attributes respectively. An attribute ∈    ⟹ is a crisp attribute and ∈    ⟹    is a vague attribute. Similarly, the role classification of the RBox classifies the relations into the crisps relations and vague relations such that, the set of roles R=    ∪ Rv where

R_c and R_v represent the set of crisp and the set of vague relations respectively. A relation r_t ∈ R_c ⟹ r_t is a crisp relation and r_t ^∈ R_v ⟹ r_t is a vague relation. Fig.3 presents our modelling architecture

An ontology is said to be of a crisp domain if = ∅ and Л _v = ∅ , otherwise, it is an ontology of a vague domain. Similarly, a concept is crisp if all roles and attributes used in its definitions are crisps. Vague elements are therefore interpreted using approximate techniques while taking into consideration the degree of available knowledge about the elements. It is worth noting that, crisp elements can still be interpreted in any classical way.

Example 1: Assume a DL representation of the following statement “ A happy father has a child and all beings he cares for are healthy ” as follow:

The definition of the concept HappyFather contains a crisp role hasChild and a crisp concept Man . However, the role careFor and the attribute Healthy are vague since one cannot quantify them with a true or false membership especially when it comes to the boundary region. They can be classified as follow: Healt ℎ У ∈ Л _v, hasChild ∈ R_c , and careFor ∈ Ry . This makes the concept HappyFather vague.

• IV.    Interpreting an Ontology of Uncertainty

Given an ontology, an interpretation function ^.I maps the concept A ∈ C to a set A ^I ⊆ ∆ ^I . In classical ontologies interpretation, the result of such mapping returns the set of individual satisfying the concept A. The concept is said to be satisfiable if there exists an interpretation for which the result does not return an empty set. That is A ^I ≠ ∅ ^. otherwise, the concept is not satisfiable. This interpretation assumes all concepts to be crisp. Consequently, if concept A is not satisfiable, then ￢ A is satisfiable. Since ￢ A ^I = ∆ ^I - A ^I .

• A.    Vague Concept Approximation

In this section, we consider the problem of approximating vague concepts over the set of individuals. Because of the vagueness in their conceptualization, such concepts are perceived only through some subsets of I. We use the rough membership to approximate them. As shown in [18], a concept can be represented as attributed valued. We therefore construct a decision table based on concepts’ attributes to approximate their rough membership. Like any information system, an ontology can be represented in a tabular form as shown in table 1. Table columns are labelled with concepts, table rows labelled with instances of interest and entries of the table are concepts values. The function f:  ×c→V is such that f(i,c)∈Vc , for every ( i,c)∈I×C represents the information knowledge of i with respect to c. Where Vc represents the set of values an instance i may have with respect to c.

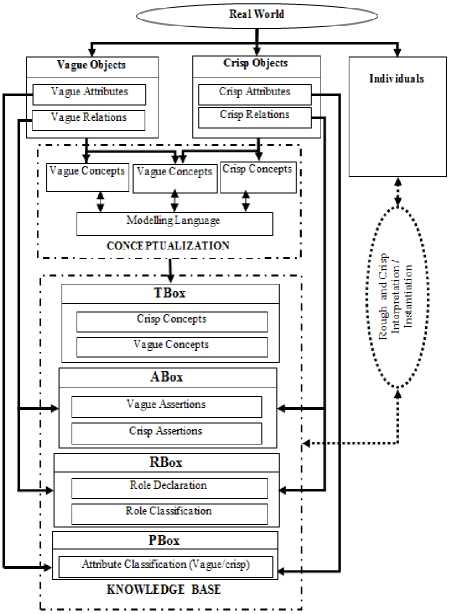
Fig.3. Ontologies of Uncertainty Modelling

Table 1. Tabular Representation of Ontology Knowledge

C I	c 1	c 2	c 3		cn
i 1	f(i 1, c 1 )	f(i 1, c 2 )	f(i 1, c 3 )		f(i 1, c n )
i 2	f(i 2, c 1 )	f(i 2, c 2 )	f(i 2, c 3 )		f(i 2, c n )
i 3	f(i 3, c 1 )	f(i 3, c 2 )	f(i 3, c 3 )		f(i 3, c n )
i k	f(i k, c 1 )	f(i k, c 2 )	f(i k, c 3 )		f(i k, c n )

Table 2. Tabular Representation of a Concept Knowledge Based on Its Attributes

B I	b 1	b 2	b 3		b n
i 1	f(i 1, b 1 )	f(i 1, b 2 )	f(i 1, b 3 )		f(i 1, b n )
i 2	f(i 2, b 1 )	f(i 2, b 2 )	f(i 2, b 3 )		f(i 2, b n )
i 3	f(i 3, b 1 )	f(i 3, b 2 )	f(i 3, b 3 )		f(i 3, b n )
i k	f(i k, b 1 )	f(i k, b 2 )	f(i k, b 3 )		f(i k, b n )

Furthermore, since it was proved in [18] that a concept can be defined by using attributes and relations with no regards to previously defined concepts, we can therefore define an attributed table for a specific vague concept say c , based on the set of attribute used in it definition as shown in table 2. Let B be a subset of the set of attributes A such that, the elements of B are the attributes used in

the expanded definition of c. let :  ×   → be a function defined such that ( , )∈   , for every

( , )∈  × represents the information knowledge of i with respect to a.

From table 2, we can now determine the rough approximation of a concept. The starting point of rough approximation is the indiscernibility relation, which is generated by information about objects of interest. Elements that exhibit the same information are indiscernible (similar) and form blocks that can be understood as elementary granules of knowledge about the universe. The indiscernibility relation expresses the fact that due to the lack of knowledge we are unable to discern some objects employing the available information. Therefore, we are unable to deal with a single object. Nevertheless, we have to consider clusters of indiscernible objects.

Given an ontology O, two individuals x, y ∈ I are said to be ci-indiscernible (indiscernible by the concept ci∈ C) if and only if x, y ∈   . Since each concept can be uniquely defined from union or intersection of the most general concept, the set of attributes, the set of relations and constructors, we can define the concepts of indiscernible objects as follow:

Definition 2: Let O = (D, C, R, A, I, £ ) be an ontology and let c ∈ C be any concept of O and let B be the subset of A ∪⊤ such that the elements of B are the attributes of the expanded definition of c. Two individuals x, y ∈ I are said to be c -indiscernible (indiscernible by the concept c) if and only if f(x, a)=f(y, a) for every a ∈ B. where f(x, a) denotes the value of the interpretation of x with respect to a.

Obviously, every concept c ∈ C induces a unique indiscernibility relation denoted by IND(c), which is an equivalence relation. The partition of I induced by IND(c) in ontology O is denoted by I/c and the equivalence class in the partition containing ∈  , denoted by [ ] . Since the vague concept c cannot be characterised by using available knowledge, two crisps set are associated to c called its lower and upper approximation.

• -    The c -lower approximation of X , denoted by _∗( ) where X is a given subset of I is defined as

_∗( )={ ∈     ℎ ℎ [] ⊆  }.       (4)

In other words, the c-lower approximation of concept c is the set of all individuals ∈ , which can be for certain classified as instances of cI

• -    The c -upper approximation of X , denoted by ^∗ ( )

where X is a given subset of I is defined as

^∗ ( )={ ∈     ℎ ℎ [] ∩  ≠ ∅ }.    (5)

In other words, the c-upper approximation of concept c is the set of all individuals ∈ , which can be possibly classified as instances of cI

• -    The c-boundary region of X is the set of all individuals ∈ , which can be classified neither as

instances of c ^I nor as instances of ￢ c ^I by employing available knowledge.

The accuracy of approximation of X with respect to c is defined as

| ∗(  )|

(  )=_| ^∗ ∗ _{( )|}                        (6)

where |X| denotes the cardinality of X. whenever the accuracy of approximation ( )=1, then, the concept is crisp.

Example 2: Assuming the following concept definition:

HealthyPerson ⊑ Person ⊓ MentallyStable ⊓ EmotionallyStable ⊓ MedicallySound

Where Person in this context is assumed to be the most general concept and MentallyStable, EmotionallyStable, MedicallySound are vague properties

Let the set of individuals I={A,B,C,D,E,F,G, H,I,J, K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y} and the set of attributes A={MentallyStable, EmotionallyStable, MedicallySound }

Let V _x denotes the set of attribute values for attribute x, defined as follow:

V MentallyStable ={High, Low, Mile}

V EmotionallyStable ={High, Low, Mile}

V MedicallySound ={High, Low, Mile}

V HealthyPerson ={High, Low}

Table 3. Decision Table of HealthyPerson

Individu als	Properties			HealthyP erson
	Mentally Stable	Emotionall yStable	MedicallyS ound
A	Low	Low	Low	Low
B	Low	Low	Low	Low
C	Low	Mild	Low	Low
D	Low	Mild	Low	Low
E	Low	Mild	Low	Low
F	Low	Low	Low	Low
G	Mild	Mild	Low	Low
H	Mild	High	Mild	High
I	Mild	High	Mild	Low
J	Low	High	Mild	Low
K	High	Low	Low	Low
L	High	Mild	Low	Low
M	Mild	Mild	Mild	High
N	Mild	High	High	High
O	Low	High	High	Low
P	Mild	Low	Low	Low
Q	High	Low	Low	Low
R	High	Low	Mild	Low
S	High	Low	High	High
T	Low	Low	High	Low
U	Mild	Low	Low	Low
V	Mild	Low	Low	Low
W	Mild	Low	Mild	Low
X	Mild	Low	Mild	Low
Y	Low	Low	Mild	Low

Assuming that, based on available knowledge which does not provide enough information to classify boundary regions individuals, the decision table of Table3 is constructed

Since the concept Person is crisp and at the same time is the most general concept, all individuals i ∈ I must be instances of Person . Therefore, in the approximation of HealthyPerson over I, there is no need of bothering about the satisfiability of person .

Let f(HealthyPerson: High)={H, M, N, S} be the approximation of   “HealthyPerson”   when it corresponding attribute value is “ High” over the set of individuals, which should be denoted in the remaining of this example as f for short.

The set of equivalent classes can be defined based on the possible properties’ values as follow:

[MentallyStable:   Low;   EmotionallyStable:

MedicallySound: Low ] = {A, B, F}

[MentallyStable:   Low;   EmotionallyStable:

MedicallySound: Low ] = {C, D, E}

[MentallyStable:   Mild;   EmotionallyStable:

MedicallySound: Low ] = {G}

[MentallyStable:    Mild ;   EmotionallyStable:    High ;

MedicallySound: Mild ] = {H, I}

[MentallyStable:    Low ;   EmotionallyStable:    High ;

MedicallySound: Mild ] = {J}

[MentallyStable:   High; EmotionallyStable:

MedicallySound: Low ] = {K, Q}

[MentallyStable:   High;   EmotionallyStable:

MedicallySound: Low ] = {L}

[MentallyStable:   Mild;   EmotionallyStable:

MedicallySound: Mild ] = {M}

[MentallyStable:    Low ;   EmotionallyStable:    High ;

MedicallySound: High ] = {O}

[MentallyStable:    Mild ;   EmotionallyStable:    High ;

MedicallySound: High ] = {N}

[MentallyStable:   Mild;   EmotionallyStable:

MedicallySound: Low ] = {U, P, V}

[MentallyStable:   High;   EmotionallyStable:

MedicallySound: Mild ] = {R}

[MentallyStable:   High;   EmotionallyStable:Low;

MedicallySound: High] = {S}

[MentallyStable:   Low;   EmotionallyStable:Low;

MedicallySound: High] = {T}

[MentallyStable:   Mild;   EmotionallyStable:Low;

MedicallySound: Mild] = {W, X}

[MentallyStable:   Low;   EmotionallyStable:Low;

MedicallySound: Mild] = {Y}

Consequently, the set of partitions of I with respect to HealthyPerson is defined as follow:

I/HealthyPerson ={{A, B, F}, {C,D,E}, {G}, {H,I}, {J}, {K,Q}, {L}, {M}, {O}, {N}, {U,P,V}, {R}, {S}, {T}, {W,X}, {Y}}

Finally,

HealthyPerson _∗( f )={{M}{N}{S}}

HealthyPerson ^∗ ( f )={{H,I},{M},{N},{S}}

Because the lower approximation is not empty, one can conclude that, Healt ℎ yPerson is absolutely satisfiable. The accuracy of approximation of f with respect to the concept HealthyPerson is

®HealthyPer son

( f ) =  =0.6

• B.    Instantiating Uncertain Individuals

Uncertain individuals are approximated as absolute or rough instance of a concept. The classification depends on whether the individual belongs to the lower approximation or boundary region respectively. By introducing the notion of absolute and rough instances, one clearly shows the degree of satisfiability of vague concepts or properties. Given a concept c ∈ C and an individual i ∈ I , the degree of membership of i with respect to a rough interpretation of c denoted by Цх ( i ) is a value in the range[0,1] defined as

^{( 1} )= ^| - _| ^∩ ∗ ₍ ^{∗ (} _)| ^)|                          (8)

Where X is a given subset of I, c ∗ ( i )the partition of X containing i and | X | denotes the cardinality of X .

For example, by using the partition of equivalent classes I/ HealthyPerson obtained in example 2, we can compute the degree of certainty of individuals f ={H ,M,N,S} classified as instances of HealthyPerson as follow:

HealthyPerson ( H ) Ц {H,M,N,S}      ()	|{ H , M , N , S }∩{ H , I }| _ 1 =       |{ H,I}|        =	(9)
HealthyPerson s Т1Д\ M {H,M,N,S}      ( м )	|{ H , M , N , S }∩{ M }| =      |{ M }|      = 1	(10)
HealthyPerson f мл P {H,M,N,S}      ( N )	|{ H , M , N , S }∩{ N }| |{ N }|       = 1	(11)
HealthyPerson ( s ) M- {H,M,N,S}       ()	|{ H , M , N , s }∩{ S }| =      |{ S }|      = 1	(12)

Consequently, H is a rough instance of HealthyPerson while M, N and S are absolute instances of HealthyPerson.

• C.    Vague Relations Interpretation

In this section, we consider the problem of approximating vague relations between sets of individuals. The conception of rough relations as defined by Pawlak¹⁹ cannot be applied directly in the case of ontologies because relations in rough set are assumed to be equivalence relations which is not always the case in ontologies. It is known that for a relation R to be an equivalence relation, it must be reflexive, symmetric and transitive. For example, assuming a relation motherOf (x,y) which specifies that, x is a mother of y . It is obvious that reflexivity e.g. MotherOf(peter, Peter), symmetric e.g. MotherOf(Mary, Peter) → MotherOf(Peter, Mary) and transitivity e.g.        MotherOf(Amina, Mary) and

MotherOf(Mary, Peter)→ MotherOf(Amina, Peter) will not hold in this context.

Because of this limitation, we extend the general binary relation based rough set [6][20][21] to derive an approximation of ontological rough relations. The general binary relation based rough set is defined based on general binary relation.

Definition 3: Let U be the universe and let R^U^U be a general binary relation on the universe. For any x ∈ U , denote R_s(x) = { (x,y) E U x U|xRy} then R(x) consists of pairs (x,y) such that y is called the successor neighbourhood of x with respect to R . For any y ∈ U, denote R_p(y) = { (x,y) E U x U|xRy} then R_p(y) consists of pairs (x,y) such that x is called the predecessor neighbourhood of y with respect to R .

In other words, given x ∈   U, the successor neighbourhood R s(x) is consisted of all pairs (x, y) which satisfy x R y and, given y ∈ U the predecessor neighbourhood ( )is the set of all pairs (x, y) which satisfy xRy. They can both be treated as classes induced by the general binary relation R. We can now define an approximation of rough ontological relations based on rough set theory.

Definition 4: Let O be an ontology and let P and Q be two approximations over I, and let r ∈ R be any vague relation of R. For any X Qxl , The X -lower approximation and the X- upper approximation of r with respect to x are defined respectively as follows.

• X .(r) = ((x,y)ePxQ|r$(x)cX)(13)

X*(r) = {(x,y) E P x Q |rs (x) А X * 0}(14)

The accuracy of approximation of X with respect to r is defined as ar (X) =(15)

rv 7     |X*(r)|

Example 3: Given I={A,B,C,D,E,F,G,H,I,J,K,L,M,N, O,P,Q,R,S,T,U,V,W,X,Y}, assume two arbitrary approximations P={A,B,C,E} and Q={B,C,D,E,F} over I. let X={(A,B),(A,D),(C,D),(E,D),(E,F)} and let cpxQ ={(A,B),(A,D),(B,C),(B,E),(C,D),(C,E),(E,D),(EF)} then, the partition defined by the successors neighbourhood with respect to r are the following:

rs (4)={(A,B),(A,D)} rs (B)={(B,C),(B,E)} rs (C)={(C,D),(C,E)}

( )={(E,D),(E,F)}

Consequently, the set of partitions of r with respect to is defined as follows:

r/r , ={{(АМШЖС)^^

,(E,F)}}

Therefore,

r * (X) = {{(A, B), (A, D)}, {(C, D), (C, E)}, {(E, D), (E, F)}} r . (X) = {{(A, B), (A, D)}, {(E, D), (E, F)}}

The accuracy of approximation of X with respect to r is ar (X)=± =0.67             (16)

• D.    Vague Relation Membership

A pair (x, y) can be approximated as absolute or rough member of a relation r depending on whether the (x, y) belongs to the lower approximation or boundary region of r respectively. The degree of membership of (x, y) with respect to r denoted by ( , ) is defined as

Й ^W(x, у А                (17)

Where X is a given subset of I, | X | denotes the cardinality of X and r_s (%) the partition defined by the r-successors of x.

From Example 3, the following membership value can be defined

^(^Ъ-л         |{(A,B),(A,D),(C,D),(E,D),(E,F)}A{(A,B),(A,D)}|

^(Л , ⁵⁾= -------------- |{(A,B),(A,D)}|-------------- ⁼¹

r_s(C) ,_{r m} _ |{(A,B),(A,D),(C,D),(E,D),(E,F)}A{(C,D),(C,E)}| _ 1 ^X       ,                         |{(C,D),(C,E)}|                    2

• E.    Vague Relations and Vague Concepts

The approximation of vague relation r as defined in section 4.3. assumes the approximations P and Q over I to be crisp approximations. If P and Q are approximation of vague concepts, we should have obtained P-upper approximation and P-lower approximation for P and Q-upper approximation and Q-lower approximation for Q. In that case, for every pair (x,y) E P x Q, four scenarios are possible:

Case1: x E BN (P) and y E BN (Q)

Case2: x E BN (P) and y EQ

• Case3:  E  . and y E    ()

• Case4:  E  . and y E

In the first three cases, one cannot talk of lower approximation of r since for each of them, either x E

( ) or E ( ). That is the instantiation of at least one of the individuals of the pair ( , ) is not certain.

Because of that, it is not possible to establish a certain relation, that is _. , between x and y when the instantiation of individuals x and y with respect to P and Q respectively is not certain.

In case 4, since E . and y E . , we are certain of the instantiation of individuals x and y with respect to P and Q respectively. Therefore, a lower approximation of r can be defined. The lower and the upper approximation of r can now be reformulated as follow:

Definition 5: Let O be an ontology and let P and Q be two approximations over I, and let r ∈ R be any vague relation of R. For any X ⊆ I×I , The X -lower approximation and the X- upper approximation of r are defined respectively as follows:

х ∗ ⁽ г )={( х , У ) ∈ А ∗ ( Р )× В ∗ ( Q ) | С ( X ) ⊆ Х} (20)

Х ^∗ ( Г )={( X , У ) ∈ A ^∗ ( Р )×B ^∗ ( Q ) | ^rs ( X )∩Х≠ ∅ } (21)

Where А ∗ ( Р ) and А ∗₍ Р ) denote the A- lower and A- upper approximation of P for some A ⊆ I such that dom(X) ⊆A. В ∗ ( Q ) and В ∗₍ Q ) denote the B -lower and B -upper approximation of Q for some B ⊆ I such that Ran(X) ⊆ B.

The rough membership of a pair (x, y) now should take into consideration the degree that x belongs to P given A, that is Ра ( X ) , the degree that y belongs to Q given B, that is Цу ( "У )and the degree that (x, y) belongs to X given r denoted by Й ( х , У ). Thus, the degree of membership of (x, y) denoted by М-х ( X , У ) is defined as

Рх ( х , У )= Ра ( х ) × Рх ⁽ X )₍ х , У )× Рв ( У )   (22)

Example 4:  Assuming the following definition:

HappyPerson ⊑ HealthyPerson ⊓ CareFor.Healthy and the set of individuals I={A,B,C,D,E,F,G,H,I,J,K,L,M,N, O,P,Q,R,S,T,U,V,W,X,Y} where HealthyPerson is a vague concept approximated as shown in example 2. That is, Healt ℎ yPerson ∗₍ f ) ={{H,  I},{M},  {N},  {S}} and

Healt ℎ yPerson ∗ ( f )       ={{M},{N},{S}}      where

f ( HealthyPerson : High)={ H,M,N,S}.

Suppose in the similar way, the vague concept Healthy is approximated to Healt ℎ У ∗ (ℎ) = {{B}, {D, E}} and Healty ^∗ (ℎ)= {{B}, {D, E}, ^∗ {A, F}} where h(Healty) ={B, D, E, F}

The approximation of the concept HappyPerson is resumed to the approximation of the relation CareFor over f ×ℎ such that

( X , У ) ∈ CareFor ⇒ x ∈ Healt ℎ yPerson ∧ У ∈ Healt ℎ У

Let g⊆ f ×ℎ ={(H,A),(H,B),(I,D),(I,E),(M,E),(N,F)} and let CareFor ={(H,A),(I,D),(I,E),(M,E)} then, the partitions defined by the successors neighbourhood with respect to g are the following:

9s ( H )={(H,A),(H,B)}

9s ( I )={(I,D),(I,E)}

9s ( M )={(M,E)}

9s ⁽ N )={(N,F)}

Consequently, the set of partitions of g with respect to 9s is defined as follows:

g/ 9s ={{(H,A),(H,B)},{(I,D),(I,E)},{(M,E)},{(N,F) }}

Therefore, g∗(CareFor)

={{(H, A),(H, B)},{(I, D),(I, E)},{(M, E)}} g_∗( CareFor ) ={{(M, E)}}

The degree of membership,

Pg ((H, A)) = P {н,м,N,S_} erso. ⁽ H )× Pg ⁽ " ⁾ ((H, B))

Healthy ( A )

9 {в,D,E,F_} ()

where

HealthyPerson zH     |{H,M,N,S}∩{H,I}|1

p{H,M,N,S}( H )=      |{H,I }|

Healthy z.      |{H,M,N,S}∩{A,F}|1

P{В,D,E,F}( A )=      |{A,F}|

×

8s ( H ⁾ ((HA)) = ^|{( H , A ),( I , D ),( I , E ),( M , E )}∩{( H , A ),( H , В )}| _ 1

Pg ((H, A)) =            |{( н,A),(H,В)}| thus,

Pg((H, A))=  ×   ×  =(27)

Finally, the approximation of HappyPerson , that is f(HappyPerson)=dom(g(careFor))

HappyPerson ∗ ( f ( HappyPerson )) ={M} HappyPerson ∗₍ f ( HappyPerson ))={H,I,M}

The degree of membership 9-HappyPerson ( H )= . The degree of membership of other individuals can be computed similarly.

V. Discussion

The key features of DL ontologies are the richness of the available constructors and their inference capability. As pointed out in Keet²², it would be a severe underusage of DL knowledge bases if one only were to deal with rough ontology by copying the Pawlak’s information system essentials without taking into consideration the richness of DL constructors as well as the flexibility of how to represent ontologies elements. For example, consider the definition of a vague concept HappyFather as follow: HappyFather ⊑ Man ⊓ ∃hasChild.Person ⊓ ∀careFor.Healthy where careFor and Healthy are vague role and vague attribute respectively. Because of the uses of the constructors ∀ and ∃ , this definition cannot be interpreted in the standard Pawlak conception of information system. However, for the universal and existential quantification ( ∀ , ∃ ) as well as the number restrictions (≥,≤), their rough interpretation can be easily defined. Let r be a vague relation, C a given concept and ℎ ⊆ I × I then,

• -    If   ∀ ( i , j ) ∈ ℎ ^∗ (r_s ( i )), j ∈ C ∗ ⁽ c¹ )  then   ∀ r. C  is

satisfiable

• -    If   ∀ ( i , j ) ∈ ℎ ∗ ( r_s ( i )), j ∈ C ∗₍ c' )  then   ∀ r. C  is

roughly satisfiable

• -    If    ∃ ( i , j ) ∈ ℎ ∗ (Г, ( i )), sue ℎ t ℎ at j ∈ C ∗ ⁽ c' ) then

∃ r . C is satisfiable

• -    If    ∃ ( i , j ) ∈ ℎ ^∗ ( r_s ( i )), sue ℎ t ℎ at j ∈ C ∗₍ c' )  then

∃ r . C is roughly satisfiable

• -    If |ℎ ∗ ( r_s ( i ))| ≥ n where |ℎ| denotes the cardinality of h , then ≥ nr. C is satisfiable

• -    If |ℎ ^∗ ( r_s ( i ))| ≥ n and |ℎ_∗( r_s ( i ))| ≤ n then both ≥ nr . C and ≤ nr . C are roughly satisfiable

• -    If|ℎ ^∗ (r_s ( i ))| ≤ n then≤ nr . c is satisfiable

A general solution to this limitations on rough ontology based on Pawlak rough set is to define a rough interpretation of all constructors of an expressive DL as well as defining a rough tableau reasoning procedure.

• VI.    Related Work

Several techniques of handling uncertainty in ontologies have been proposed. A good survey of early works in that direction is presented [3]. Although some techniques based on rough set have been proposed, most techniques are based on probability and the fuzzy logic. They differ mostly on the ontological language considered, the supported forms of fuzzy knowledge, and the underlying fuzzy reasoning formalism.

• [22]    augments SROIQ(D) and their application infrastructures together with rough set. The author shows that rough concepts can be dealt with in the mapping layer that links the concepts in the ontology to queries over the data source. He experimented his approach with rough concepts and vague instances using the HGT ontology with the HGT-DB database and septic patients. [23] is the same as [24] except that the language considered is OWL2.

A probabilistic generalization of RDF, which allows for representing terminological probabilistic knowledge about classes and assertional probabilistic knowledge about properties of individuals was presented in[24]. The authors provide a technique for assertional probabilistic inference in acyclic probabilistic RDF theory, which is based on the notion of logical entailment in probabilistic logic, coupled with local probabilistic semantics.

• [25]    suggested an extension of the OWL called PROWL, that provides a consistent framework for building probabilistic ontologies. The probabilistic semantics of PR-OWL is based on multi-entity Bayesian networks. PR-OWL combines the expressive power of OWL with the flexibility and inferential power of Bayesian logic.

BayesOWL [26] is a probabilistic generalization of OWL which is based on standard Bayesian networks. BayesOWL is used to quantify the degree of overlap or inclusion between two concepts. It provides a set of rules and procedures for the direct translation of an OWL ontology into a Bayesian network, and it also provides a method for incorporating available probability constraints when constructing the Bayesian network. The generated Bayesian network preserves the semantics of the original ontology and is consistent with all the given probability constraints.

OntoBayes [27] is an ontology-driven model, which integrates Bayesian networks (BN) into the OWL to preserve the advantages of both. It defines additional OWL classes which can be used to markup probabilities and dependencies in OWL files. From the perspective of ontologies, the OntoBayes model preserves the ability to express meaningful knowledge in very large complex domains and extent ontologies to probability annotated OWL to facilitate meaningful knowledge representation in uncertain systems. From the perspective of probabilistic modelling, the model takes the advantage of powerful knowledge representation ability from ontologies, to scale up the ability to do uncertain reasoning.

Pronto[28][29] is a non-monotonic probabilistic reasoner for expressive DL developed in order to perform a probabilistic reasoning in the semantic web. Pronto reason about uncertainty in OWL ontologies by establishing the probabilistic relationships between OWL classes and probabilistic relationships between an OWL class and an individual. One of the principal requirements for pronto is that the uncertainty could be introduced into OWL ontologies and that existing OWL reasoning services should be retained. To meet that requirement, Pronto is designed on top of the OWL reasoner to provide routines for higher level probabilistic reasoning procedures.

A fuzzy extensions of an expressive classical DL SHIN which improves the knowledge expressiveness of ALC by allowing constructors including number restriction, inverse role, transitive role, and role hierarchy was presented in [30]. The authors provide a tableaux calculus for fuzzy SHIN without fuzzy general concept inclusions. Its semantics is based on Zadeh logic.

FuzzyDL [31] is an expressive is a DL reasoner supporting fuzzy logic reasoning. The reasoning algorithm uses a combination of a tableaux algorithm and a Mixed-integer linear programming (MILP). fuzzyDL extends the classical DL SHIF(D) to the fuzzy case. But in addition to the constructs of SHIF(D) it allows some new concepts constructs such as weighted concepts (n C) , weighted sum concepts (n₁C₁ + · · · + n_kC_k) and threshold concepts (C[≥ n]) and (C[≤ n]) where C is a concept and n the weight. The degrees of the fuzzy axioms may not only be numerical constants, but also variables, thus being able to deal with unknown degrees of truth. The most interesting feature of fuzzyDL is the expressivity of the representation language.

An algorithm to perform a query-specific reasoning method for inconsistent and uncertain ontologies without revising the original ontologies was proposed in [32]. Their reasoning method adopts a selection function, which is capable of selecting elements related to a specific query. Thus, the elements necessary for the reasoning could be obtained fast and the query results could be returned efficiently. Apart from the true or false answer, the results of the query achieved by their method also include the specific reasoning route (path) and certainty degree of each answer. In this way, the user may obtain more useful information to facilitate his selection of the most credible query result according to the certainty degree of each result.

An extension of description logics using possibilistic logics to reason with inconsistent and uncertain knowledge was proposed in [33]. The authors define the semantics and syntax of possibilistic description logics. The authors also define two inference services in possibilistic description logics named possibilistic inference and a variation, named linear order inference. The algorithms for possibilistic inference of the proposed logics is independent of DL reasoner.

An approach of addressing the problem of representing uncertainty based on the Dempster–Shafer theory was proposed in [1]. The authors modelled a Dempster-Shafer upper level ontology that can be merged with any specific domain ontology and to instantiate it in an uncertain manner. To reason about the uncertain objects contained in the ontology, the authors implement a Java application based on Jena framework. The Jena framework is a tool to retrieve the instances associated to each individual uncertain concept, and the Dempster-Shafer information collected. This information is then transmitted to a common basic Dempster-Shafer library which then performs calculations in the Dempster-Shafer theory. Finally, decision criteria can be applied to extract the chosen hypothesis, either based on the maximum of plausibility or belief function or either on probability criteria, etc.

A tableaux algorithm for computing the inconsistency degree of a knowledge base in possibilistic DL ALCIR+, which extends possibilistic DL ALC with inverse roles and transitive roles was proposed in [34]. The authors proposed a blocking condition to ensure the termination of their algorithm.

• VII.    Conclusion

This paper has presented an approach of modeling uncertainty in ontologies as a result of the shortcoming of classical ontologies not being able to represent vague or incomplete knowledge of an application domain. Since the source of vagueness in ontologies is from vague attributes and vague relations, concepts are therefore clearly classified as crisp or vague concepts depending on whether vague attributes or vague relations are used in their conceptualization or not. The approximation of the degree of instance of individuals with respect to a given concept or relation is therefore evaluated based on the rough membership as defined in Pawlak rough set. Subsequent works look into achieving a satisfiability reasoning of complex construct of expressive description logic language. This will be based on providing an extension of the tableau-based algorithm with a rough interpretation of various constructors defined in SROIQ which is an expressive description logics in which the core logic of OWL is based upon.