Моделирование аргументации в научно-популярном дискурсе с использованием онтологий

Важным фактором развития современной науки является наличие доверия к ней со стороны общества и государства. Наука становится сложнее, проблемы, которые она решает – специфичнее, воспринимать и оценивать результаты научной деятельности для неподготовленной аудитории становится труднее. Ситуация, в которой учёный должен представлять свои научные идеи и разработки внешнему для его науки эксперту или потребителю (в виде заявок на гранты, научно-популярной или учебной литературы), вынуждает его переходить со специализированного языка науки на максимально приближенный к потребителю научных знаний язык обыденного мышления и убеждения. Это создаёт условия для проникновения в язык науки аргументирующего дискурса и специфических риторических средств убеждения. В данном исследовании «дискурс» понимается как единство двух сущностей — про- цесса языковой коммуникации и получающегося в её результате объекта, т.е. текста. Благодаря этому дискурс можно изучать как разворачивающийся во времени процесс и как структурный объект.

Научно-популярный дискурс является менее формальным, чем язык науки, но в то же время более строгим, чем обычный естественный язык. В нём, как правило, присутствуют аргументы (убеждающие элементы) «за» или «против» той или иной концепции/теории, используются аргументативные стратегии и риторические приёмы, реализующие различные способы убеждения.

В связи с этим возникает необходимость в более пристальном исследовании научнопопулярного дискурса как жанра человеческой коммуникации, тем более, что он намного слабее изучен по сравнению с другими жанрами, например, текстами научных статей и новостных сообщений. Особенно остро стоит проблема изучения способов аргументации и риторических приёмов, используемых в научно-популярных текстах, с целью выработки рекомендаций по написанию убедительных статей, рассчитанных на широкую аудиторию.

В работе рассматривается подход к моделированию аргументации, встречающейся в научно-популярной литературе, и анализу используемых в ней схем аргументации, аргумен-тативных стратегий и риторических приемов. Моделирование аргументации предполагает онтологическое описание схем (моделей) аргументации, их реализаций и примеров использования в исследуемых текстах. На основе онтологии строится инструмент анализа используемой аргументации, предоставляющий исследователям возможность находить и выделять в исходных текстах фрагменты, составляющие контент аргументации, и выполнять анализ стратегий и приёмов, используемых в конкретном тексте или в целом корпусе текстов.

В разделе 1 приведены краткие сведения из теории аргументации. В разделе 2 представлена информационная модель аргументации, которая используется для моделирования и анализа аргументации во многих приложениях и реализована в виде онтологии аргументации. В разделе 3 описана расширенная онтология аргументации, дополненная средствами, необходимыми для моделирования аргументации, используемой в научно-популярном дискурсе. В заключении подводятся промежуточные итоги работы по созданию расширенной онтологии аргументации и намечены планы на будущее.

1    Краткие сведения из теории аргументации

Теория аргументации – это комплексная дисциплина, существующая на стыке ряда наук, занимающихся изучением человеческой коммуникации и познания: логики и философии, истории и социологии, лингвистики и психологии, информатики и искусственного интеллекта. Теория аргументации изучает способы воздействия на убеждения людей. [1]. Это ссылки на экспертов, на опыт, на более общие принципы, на традицию, на здравый смысл и т.д.

Аргументация – это приведение доводов (аргументов) с целью изменения или формирования некоторого убеждения (позиции) у другой стороны [2]. Следует заметить, что под аргументацией понимают не только процедуру приведения аргументов в поддержку или против какого-то положения, но и саму совокупность таких аргументов.

Задача обнаружения аргументов и их составляющих в тексте (дискурсе) осложняется тем, что не все элементы аргументации явно представлены в тексте. Поэтому часто анализ аргументации начинается с восстановления последовательности (набора) высказываний (посылок), приводящих к некоторому заключению (утверждению).

Предложено много различных моделей аргументации [3], каждая из которых опирается либо на логический, либо на когнитивный, либо на риторический подход, либо на ту или иную их комбинацию, потому что, как верно замечено в [4], в отдельности ни один из этих подходов не может дать нам точной картины аргументации, содержащейся в конкретном тексте. Одной из самых влиятельных моделей аргументации является модель Тулмина [5]. Согласно этой модели аргумент в общем случае включает шесть элементов (см. рисунок 1):

• ■    Claim - тезис, т.е. утверждение или заключение, представленное аудитории (оно может не соответствовать первоначальным убеждениям аудитории);

• ■    Data - исходные данные (факты, утверждения, посылки), относящиеся к рассматриваемой ситуации и которые являются основой для принятия тезиса;

• ■    Warrant - утверждение, обосновывающее вывод тезиса из данных;

• ■    Backing - информация, поддерживающая утверждения;

  

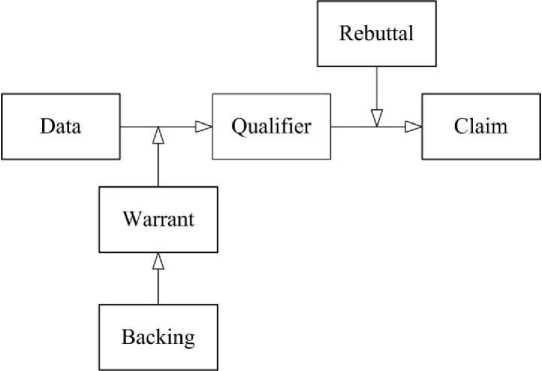
  Рисунок 1 – Модель аргументации Тулмина

  
  

• ■    Rebuttal      -      утверждение,

описывающее          границы применимости   аргумента, т.е.

ситуацию, когда тезис не может быть принят;

• ■    Qualifier - утверждение, выражающее степень уверенности в тезисе.

Обязательными элементами аргумента считаются Claim, Data и Warrant , а остальные элементы могут отсутствовать.

В этой модели контраргументы также являются аргументами, которые могут «атаковать» любой из первых четырёх элементов ( Claim, Data,

Warrant или Backing ).

На практике приходится иметь дело не с одним, а с множеством аргументов. При этом любой аргумент может стать отправной точкой (посылкой) для другого аргумента. Любой тезис может рассматриваться как потенциальное обоснование другого тезиса. У разных аргументов могут быть общими как посылки, так и тезисы. Таким образом, аргументы оказываются связанными, и из них образуется сеть аргументов. На практике сеть аргументов обычно представляется в виде графа, поэтому в дальнейшем использованы термины граф аргументов или граф аргументации .

Многие известные модели аргументации опираются на приведённую выше модель Тулмина. Можно выделить три категории моделей аргументации: риторическую, диалогическую и монологическую [6]. Первые две выделяют аргументацию как динамический процесс: риторические модели делают акцент на аудиторию и на убедительное намерение, а диалогические описывают способы, которыми аргументы связаны в диалоговых структурах. Монологическая модель вместо этого подчеркивает структуру аргумента, включая отношения между различными компонентами данного аргумента.

Другая известная классификация моделей аргументации включает абстрактную и структурированную аргументации [7]. Абстрактная аргументация рассматривает каждый аргумент как атомную сущность без внутренней структуры. Структурированной аргументацией принимается во внимание внутренняя структура каждого аргумента.

При анализе аргументации, используемой в текстах, когда требуется извлекать элементы аргументов из фрагментов текста на естественном языке, структура аргумента играет важную роль. Поэтому при решении таких задач используются модели структурированной аргументации. Наиболее известной моделью структурированной аргументации, нашедшей при- менение в практических системах анализа аргументации, является модель Дугласа Уолтона [8]. В этой модели структурированный аргумент определяется как набор утверждений, состоящий из трёх частей: набора посылок, заключения и вывода из посылок к заключению.

Схемы аргументации в модели Д. Уолтона – это формы аргументов, описывающие структуры аргументативного вывода [9]. Это понятие позволяет выявлять и оценивать общие типы аргументации. Такие схемы могут использоваться для представления знаний, необходимых для приведения аргументов и объяснений. Они отражают стереотипные модели мышления, которые в общем случае не являются дедуктивными и монотонными. Такие схемы аргументов называют моделями правдоподобного вывода, в том смысле, что, если посылки аргумента верны, то предположительно верно и заключение.

Каждая схема имеет название, заключение, набор посылок и набор критических вопросов. Критические вопросы дают возможность определить слабые стороны аргумента, основанного на этой схеме. Их можно использовать для моделирования дополнительных посылок или порождения не представленных явно в тексте или опущенных в рассуждении посылок, которые будут поддерживать аргумент.

В работе [10] приведён компендиум, содержащий 60 основных схем аргументации, многие из которых имеют варианты (подсхемы). При этом некоторые схемы не включены в компендиум и обсуждаются отдельно. Схемы аргументов используются в ряде инструментов для анализа аргументации (Araucaria [11], OVA [12], Carneades [13], ArgDF [14]).

2    Информационная модель аргументации

Для моделирования аргументации использована онтология аргументации, базирующаяся на формате AIF (Argument Interchange Format) [15, 16], принятом международным сообществом в качестве стандартной нотации для описания аргументов и аргументативных структур. Этот формат показал себя удобным для обмена данными, полученными пользователями разных систем, в которых результаты анализа аргументации представлены в разных форматах и на разных языках [17].

• 2.1    Формат AIF

Формат AIF представляет собой онтологию, включающую понятия, необходимые для описания аргументов. Базовая AIF-онтология делится на две части: онтологию верхнего уровня и онтологию форм. Первая определяет основные строительные блоки AIF-графов аргументов, типы вершин и ребер. Онтология форм обеспечивает концептуальное описание элементов AIF-графов, таких как посылки, заключения, схемы логического вывода, исключения и т.д. Вершины, определённые в онтологии верхнего уровня, используются для построения сети аргументов на уровне экземпляров. Вершины этих сетей заполняют формы соответствующих аргументов из онтологии форм.

На рисунке 2 представлена спецификация формата AIF. Здесь белые вершины соответствуют классам онтологии верхнего уровня, серые вершины – классам онтологии форм. Разные типы стрелок обозначают различные типы отношений между классами онтологии. Сплошные стрелки указывают, что класс Схема вывода является подклассом класса Схема ; «точечные» стрелки показывают, что экземпляр класса RA-вершина реализует (fulfils) подкласс класса Схема вывода ; пунктирные стрелки указывают на то, что подклассы класса Схема дедуктивного вывода всегда имеют связанные подклассы класса Посылка .

Согласно формату AIF аргументы могут представляться как вершины в ориентированном графе, называемом сетью аргументов. Вершина может иметь ряд собственных (внутренних) атрибутов, соответствующих, например, автору аргумента, дате создания, степени до- стоверности, статусу приемлемости аргумента и т.п. Поскольку эти атрибуты зависят от конкретного приложения, они не задаются в AIF-онтологии.

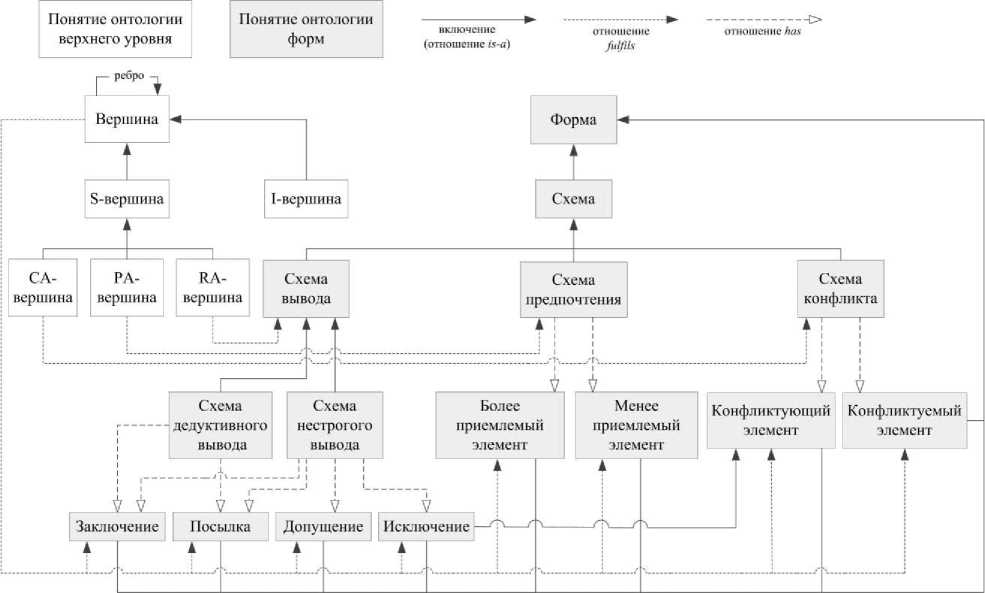
Рисунок 2 - Спецификация формата AIF

Формат AIF определяет два непересекающихся типа вершин: информационные вершины ( I-вершины ) и вершины-схемы ( S-вершины ). I-вершины используются для представления утверждений, содержащих информацию, связанную с такими элементами аргумента, как заключения, посылки, допущения и т.п. S-вершины служат для представления схем аргументов, которые являются предметно-независимыми шаблонами (моделями) рассуждений. Эти схемы похожи на правила вывода в дедуктивной логике, но расширены возможностью поддержки других типов вывода. Элементами схем аргументов являются посылки, допущения, исключения и заключение.

Формат AIF содержит три непересекающихся типа S-вершин : вершины реализации правил вывода ( RA-вершина ), вершины реализации предпочтения ( PA-вершина ) и вершины реализации конфликта ( CA-вершина ). Слово «реализация» для этих типов означает, что эти вершины функционируют как экземпляры, а не классы. К RA-вершинам относятся вершины, представляющие как дедуктивные правила вывода, так и правила правдоподобного (нестрогого) вывода, СА-вершины служат для задания отношения конфликта (например, между утверждением и его отрицанием), а PA-вершины реализуют отношение предпочтения среди оцениваемых вершин.

• 2.2    Сеть аргументов

Спецификация формата AIF не задаёт типы рёбер (связей). Семантика связей может быть выведена из типов вершин, которые они соединяют. Есть два вида рёбер:

• ■    рёбра схемы, исходящие из S-вершин ; они поддерживают заключения других S-вершин, которые могут быть как I -вершинами , так и S -вершинами ;

• ■    рёбра данных из I-вершин в S-вершины , которые предоставляют информацию (посылки) для реализаций схем аргументов.

То есть, существуют рёбра вида I-to-S (рёбра информации), S-to-I (рёбра вывода) и S-to-S (рёбра обоснования). Из приведённых ограничений видно, что рёбра, исходящие из I-вершин, не могут быть направлены в другие I-вершины . Это гарантирует, что отношения между двумя элементами информации будут определены явно через промежуточную S-вершину . Для заданной сети аргументов вершина A поддерживает вершину B тогда и только тогда, когда существует ребро от A к B .

Сеть AIF-аргументов является диграфом G = (N,E), где:

• ■    N = I U RA U CA U PA - множество вершин, где I - множество I-вершин, RA - множество RA-вершин, CA - множество CA-вершин, PA - множество PA-вершин ;

• ■    E £ (N х N) 1 (I х I) - множество рёбер.

• 2.3    Реализация AIF-онтологии

На рисунке 3 представлена сеть аргументов, связанных различными типами конфликтных отношений. В этой сети экземпляры аргументов обозначены как Arg n , посылки как PX n , выводы – CX , допущения – AsmX n , исключения – ExcpX n , а экземпляры общего конфликта и конфликта с исключением как GC n и EC 1 соответственно (в обозначениях X ∈ { A, B, C, … } и n ∈ N ).

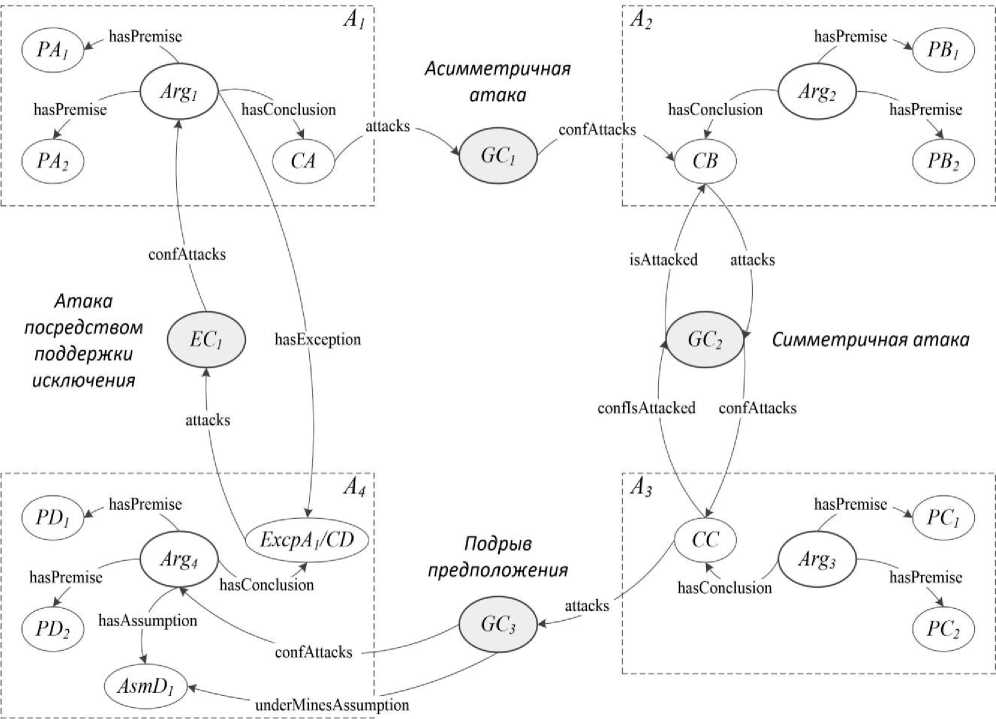
Рисунок 3 – Сеть аргументов с различными отношениями конфликта

Здесь показаны четыре различных типа конфликтов между аргументами: асимметричная атака ( Arg 1 против Arg 2 ), симметричная атака ( Arg 2 и Arg 3 атакуют друг друга), подрыв допущения ( Arg 3 против Arg 4 ) и атака посредством поддержки исключения ( Arg 4 против Arg 1 ).

Первая версия AIF-онтологии была реализована на языке RDFS [18]. Она использовалась для описания аргументов и схем аргументации. На базе этой онтологии была построена пилотная web-система ArgDF [14], которая позволяла создавать структуры аргументов в RDF-хранилище и осуществлять в нем поиск. Позже AIF-онтология была реализована на языке OWL DL [18, 19] и на сегодняшний день является единственной доступной версией AIF-онтологии [20], поэтому её можно называть базовой AIF-онтологией. Её выразительность значительно выше, чем у версии онтологии на языке RDFS. В частности, в ней дано определение спецификации AIF-формата и схем аргументов в виде классов (в отличие от экземпляров классов в RDFS-версии), что позволяет явно классифицировать сами схемы. Новая версия онтологии позволяет явно использовать машины вывода для классификации аргументов и схем. В эту версию онтологии включено около 40 схем аргументации из компендиума Уолтона [10]. В описания схем аргументации в качестве дополнительных посылок-утверждений введены допущения и исключения, построенные на основе приведённых в схемах Уолтона критических вопросов.

Рассмотренная AIF-онтология предназначена только для представления аргументов и ар-гументативных структур. Для решения задач анализа аргументации, таких как оценка качества аргументации, поиск более приемлемых аргументов и др., данную онтологию необходимо дополнить соответствующими классами, отношениями и атрибутами.

3    Расширение онтологии аргументации

Для решения задач извлечения аргументов из текстов и анализа аргументации базовая AIF-онтология дополнена средствами, позволяющими моделировать аудиторию, на которую направлены аргументы, и средствами, позволяющими представлять содержание утверждений, входящих в аргументы. На рисунке 4 представлена модификация базовой онтологии AIF, реализующая предложенные дополнения.

• 3.1    Средства моделирования аудитории

При анализе аргументации часто требуется учитывать образ мышления и систему ценностей различных аудиторий. Например, аргументы, значимые для подростков, в частности, апеллирование к мнению социальной группы, могут оказаться менее значимыми для старшей аудитории. В то же время отсылки на мнение авторитетных учёных будут более значимыми для научных работников, чем для школьников.

Для работы со значимостью (весомостью) аргументов и их посылок в базовую AIF-онтологию введены веса, как атрибуты классов схем аргументов, элементов схем аргументов и собственно утверждений. В работе [21] разработана модель – абстрактная алгебра, которая в сочетании с AIF-онтологией позволяет при анализе значимости аргументов также использовать веса их элементов, в том числе с учётом атак, поддержек и агрегирования аргументов. (Агрегирование используется в ситуации, когда одно утверждение выступает в роли заключения сразу в нескольких аргументах.) При вычислении веса заключения аргумента учитываются веса посылок и связи с остальными аргументами сети.

В расширенной онтологии эта модель дополнена возможностью учёта веса схемы аргумента, поскольку для различных аудиторий одна и та же схема аргумента может иметь разный вес. Например, в научной среде аргумент «От аналогии» (схема №7 в компендиуме [10]) может иметь низкий вес, в то время как для юристов этот аргумент достаточно веский, если система права основана на прецедентах. Введены средства учёта весов таких элементов схемы аргумента, как допущения и исключения.

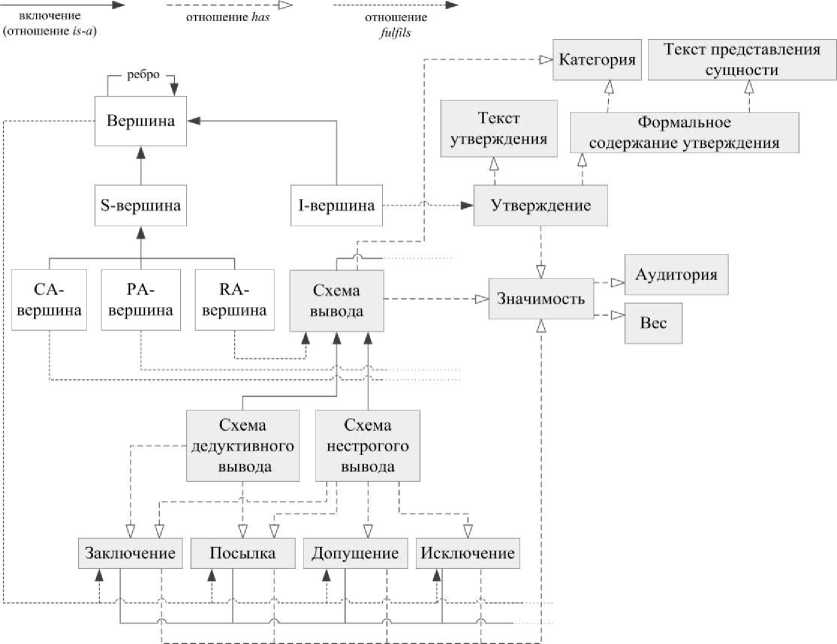
Рисунок 4 – Модификация базовой онтологии AIF

Веса, зависящие от аудитории, задаются с помощью класса Значимость , содержащего пары атрибутов Аудитория и Вес . Атрибут Аудитория содержит обозначение целевой аудитории. Атрибут Вес может задаваться как целым числом, так и вещественным числом от 0 до 1. В последнем случае при вычислении весов аргументов применяется нормирование.

Оценивание качества (обоснованности/убедительности) аргументации основано на использовании весов заключений аргументов. Существуют различные способы вычисления веса заключений анализируемых аргументов [21, 22]. Способы вычисления весов аргументов, построенных на расширенной онтологии, будут использовать веса схем аргументов, веса их посылок, допущений и исключений, веса конкретных утверждений, извлечённых из текста и составляющих содержание посылок, допущений и исключений ( I-вершин ), а также отношения поддержки и атаки других аргументов сети.

• 3.2    Средства описания содержания аргументов

В базовой AIF-онтологии в схемах аргументов на уровне структуры аргумента присутствуют посылки и заключения, допущения и исключения, которые являются утверждениями. В этих утверждениях можно выделить предметно-независимые понятия и отношения, такие как источник информации, персона, действие, цель, принадлежность и т.п. Эти понятия и отношения могут служить для установления референтных связей между аргументами, что может быть полезно как при «ручном», так и автоматизированном анализе структуры сети аргументов. По этой причине в онтологию введены средства, позволяющие представлять содержание утверждений, входящих в аргументы, в виде экземпляров таких понятий и отношений. Варианты детализации описания утверждений показаны на следующих примерах схем аргументов.

Схема «От экспертного мнения» (схема №2 в компендиуме [10]) имеет вид:

Посылка 1 : источник E является экспертом в предметной области S .

Посылка 1' : утверждение A относится к предметной области S .

Посылка 2 : E утверждает, что A истинно (ложно).

Вывод : A истинно (ложно).

Критические вопросы :

• 1)    Можно ли доверять E как эксперту?

• 2)    Является ли E экспертом в той области, которой принадлежит A ?

• 3)    То, что утверждал E , действительно влечёт A ?

• 4)    Надёжен ли E как источник информации?

• 5)    Согласуется ли мнение E об A с мнением других экспертов?

• 6)    Основано ли утверждение E на фактах?

Предметно-независимыми понятиями в этой схеме являются источник информации E (им может быть как персона , так и, например, статья _в_журнале ), предметная область S и утверждение A . Они связаны предметно-независимыми отношениями являться _экспер-том(Е, S, true) , принадлежать(A, S, true) и утверждать(Е, A, true) , быть_истинным(A, true/false) . Здесь и далее элементы отношений true или false обозначают истинность отношения в данном утверждении.

В критических вопросах этой схемы, поскольку они служат основаниями для формирования исключений и допущений аргумента, также необходимо выделять предметнонезависимые понятия и отношения. В приведённом аргументе - это: являться_экспертом(Е, S, го) , влечёт^, A 2 , to) , согласуется^, A 2 , to) , оценивать(Р, надёжность, го) , обосновано^, го) . Здесь го используется для неопределённого значения истинности (в понятиях из критических вопросов).

Схема «От взаимосвязи персоны и действия» (схема №18.1 в компендиуме [10]) имеет вид:

Посылка 1 : персона P осуществила действие A .

Посылка 2 : действие A оценивается значением V .

Вывод : персона P оценивается как V .

Предметно-независимыми понятиями в этой схеме являются персона P , действие A и оценка V . Они связаны предметно-независимыми отношениями сделать(Р, A, true) , оцени-вать(A, V, true) и оценивать(Р, V, true) .

Если в сети аргументов одна и та же персона встречается и как эксперт (в схеме №2), и как персона( в схеме №18.1), то автоматическое обнаружение такого соответствия может подсказать пользователю существование возможной атаки «Посредством поддержки исключения» второго аргумента на первый.

Например, пусть сеть аргументов содержит два аргумента, реализующих схемы «От экспертного мнения» и «От взаимосвязи персоны и действия» (см. рисунок 5).

Пусть аргумент «От экспертного мнения» имеет вид:

Посылка 1 : X преподаёт в известном университете предмет «Методы анализа данных».

Посылка 1' : методы машинного обучения изучаются в области анализа данных.

Посылка 2 : Х утверждает, что методами машинного обучения невозможно извлечь полную семантическую информацию.

Вывод : можно считать, что методами машинного обучения невозможно извлечь полную семантическую информацию.

Допущение/исключение, сформированное на основе критического вопроса №4 содержит отношение оценивать(X, надёжность, ω). В сети аргументов может существовать аргумент, вывод которого однозначно определяет значение го. Если этот вывод определяет го как true, то этот аргумент поддерживает аргумент «От экспертного мнения», а если он определяет ω как false, то этот аргумент атакует его.

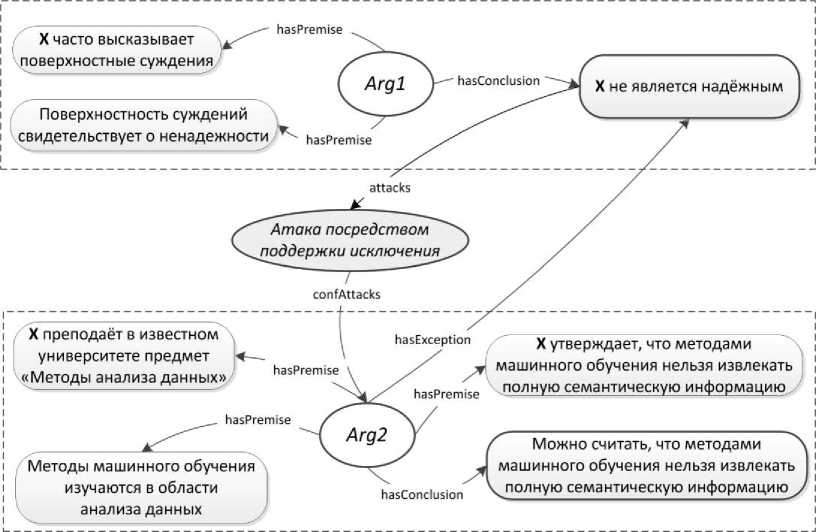
Рисунок 5 - Пример атаки посредством поддержки исключения

Пусть в этой же сети аргументов также имеется аргумент «От взаимосвязи персоны и действия» следующего вида:

Посылка 1 : X часто высказывает поверхностные суждения.

Посылка 2 : поверхностность суждений свидетельствует о ненадёжности.

Вывод : X не является надёжным.

Утверждение вывода этого аргумента содержит отношение оценивать(X, надёжность, false) . Поэтому в данном случае аргумент «От взаимосвязи персоны и действия» атакует аргумент «От экспертного мнения». Вид этой атаки: «Атака посредством поддержки исключения».

Таким образом, описание формального содержания утверждений, входящих в аргументы, может быть полезным как при анализе сети аргументов, так и текста, на основе которого она была построена. Наличие таких описаний позволяет получить следующие новые возможности в моделировании и анализе аргументации:

• ■    определение связи аргументов на уровне предметно-независимых сущностей;

• ■   автоматическое предсказание отношений поддержки и конфликта;

• ■    автоматическое предсказание аргументов;

• ■    автоматизированное выявление аргументов.

Для описания формального содержания утверждений набор свойств класса Утверждение , включает атрибут Текст_Утверждения , служащий для записи текста утверждения, дополняется объектным отношением иметь_Формальное_содержание. Оно связывает данное утверждение с его формальным описанием, представленным экземплярами класса Формаль-ное_содержание . Класс Формальное_содержание имеет пару атрибутов Категория и Тек-стовое_представление_Сущности , где атрибут Категория описывает категорию некоторой сущности, встретившейся в тексте утверждения, а атрибут Текстовое_представ-ление_Сущности представляет её текстовое описание в анализируемом утверждении.

Для каждой схемы аргументов заранее задаётся свой набор Категорий для того, чтобы ограничить типы сущностей, присутствующих в схеме (например, Персона , Действие , Ценность и т.п.). Это позволяет упростить процесс извлечения сущностей, их аргументов и повысить качество анализа аргументации.

Заключение

В работе представлен подход к моделированию и анализу аргументации, встречающейся в научно-популярной литературе. Моделирование аргументации выполняется средствами онтологии аргументации, основанной на базовой AIF-онтологии и расширенной средствами, необходимыми для моделирования аргументации, используемой в научно-популярном дискурсе. В терминах этой онтологии описываются схемы аргументации, структура и элементы аргументов, а также могут представляться составные части аргументов, извлечённые из исследуемых текстов, и сети таких аргументов.

Благодаря добавлению в базовую онтологию средств, позволяющих учитывать ценности и образ мышления аудитории, для которой предназначен анализируемый научнопопулярный текст, стала возможной оценка обоснованности и убедительности аргументации для данной аудитории. Введение в онтологию средств для представления содержания утверждений, входящих в аргументы, позволяет устанавливать связи аргументов на уровне предметно-независимых сущностей и автоматически предсказывать ситуации поддержки и атаки одних аргументов другими.

На основе предложенной онтологии строится программный комплекс, предоставляющий средства для моделирования и извлечения аргументации на корпусе научно-популярных текстов, а также для исследования полученной аргументации с целью выявления и анализа используемых в текстах аргументативных стратегий и риторических приемов.

Статья подготовлена по итогам исследования, проведённого в рамках проектов Российского фонда фундаментальных исследований № 18-00-01376 (18-00-00889) и № 18-00-01376 (18-00-00760).