Моделирование биржевых колебаний в низковолатильные и высоковолатильные периоды

Автор: Кириллов Кирилл Валерьевич

Журнал: Вестник Донского государственного технического университета @vestnik-donstu

Статья в выпуске: 7-8 (75) т.13, 2013 года.

Бесплатный доступ

Анализируется моделирование колебаний цен на акции. Применение статистических критериев позволяет сделать выводы о пригодности исследуемых моделей. Наряду с широко известными критериями Колмогорова-Смирнова и Андерсона-Дарлинга применяются критерии Кристофферсона и Берковича, которые были сравнительно недавно разработаны для оценки интервальных прогнозов. Критерий Берковича особенно ценен для оценки экстремальных скачков цен в высоковолатильные периоды, так как он даёт хорошие результаты и в том случае, когда количество наблюдений невелико. Показано, что традиционно применяемые модели временных рядов с нормальным распределением и распределением Стьюдента применимы только в относительно стабильные периоды. В условиях нестабильности на финансовых рынках необходимы модели, с помощью которых можно описать высокую вероятность больших скачков цен. Анализируется модель временного ряда с распределением «с тяжёлыми концами». На основе проведённых расчётов формулируются рекомендации по управлению фондовым портфелем в кризисные периоды.

Еще

Arma-garch модель, временные ряды, распределения "с тяжёлыми хвостами"

Короткий адрес: https://sciup.org/14250028

IDR: 14250028 | DOI: 10.12737/2014

Текст научной статьи Моделирование биржевых колебаний в низковолатильные и высоковолатильные периоды

Введение. В последнее время, в связи с усложнением механизмов, лежащих в основе финансовых рынков и институтов, для того, чтобы принять правильное, взвешенное решение и выработать грамотную стратегию поведения, необходимы математические модели, учитывающие всё большее количество факторов. Наибольший интерес с научной точки зрения представляет изучение изменчивости рыночного процесса. Ключевым параметром, который численно её характеризует, является волатильность. Aвторегрессионные гетероскедастичные модели определения волатильности (ARCH, GARCH, и др.) позволяют учесть эффект кластеров на рынке, когда торговля достаточно хорошо может быть разделена на периоды низкой и высокой волатильности. В модели авторегрессионной условной гетероскедастичности ARCH [1] каждому дню присваивается свой вес, убывающий по мере удаления от текущей даты. Модель GARCH [2] вовлекает в вычисления значения волатильностей, вычисленные на предыдущих шагах. Поскольку рынок обладает памятью, необходимо эту память учитывать. Для сравнения эффективности в настоящей работе была рассмотрена модель J. P. Morgan (1996) экспоненциально взвешенного скользящего среднего EWMA. Преимущество EWMA-модели заключается в том, что для её реализации необязательно хранить большое количество данных. В любой момент времени достаточно помнить только текущую оценку дисперсии и последнее измеренное значение рыночного показателя. Измерив новое значение рыночного показателя, можно вычислить новое суточное относительное изменение и получить новую оценку дисперсии. При этом вклад доходности каждого периода экспоненциально убывает по мере его удаления в прошлое.

Для того чтобы понять, какую же из существующих моделей выбрать в качестве основы при моделировании биржевых колебаний, необходимо проанализировать свойства соответствую-

Работа выполнена при поддержке стипендии Президента России (2011—2012 гг.).

щих временных рядов. Множество проведённых исследований выявили целый ряд специфических особенностей временных рядов доходности финансовых активов и их волатильности — отсутствие автокорреляции, лептокуртозис (высокие пики и «толстые хвосты» распределения), длительная память, кластеризация волатильности, условная гетероскедастичность, эффект «рычага» и другие. Более подробный обзор этих особенностей можно найти в [3].

Дальнейшее развитие этих моделей пошло в двух направлениях. Некоторые исследователи сделали акцент на отслеживании резких скачков доходности с помощью модели Пуассоновских скачков [4]. Другой подход заключался в попытке заменить нормальное распределение распределением с более «тяжёлыми хвостами» [5—8]. Выше уже упоминалось, что финансовые ряды обычно характеризуются большой величиной куртозиса. Модель GARCH частично учитывает это, поскольку в ней безусловное распределение имеет «толстые хвосты». Это является результатом стохастического характера условной дисперсии. Однако, как правило, этот эффект не полностью улавливается моделью GARCH, что проявляется в том, что нормированные остатки модели всё ещё характеризуются большой величиной куртозиса. Таким образом, не выполняется одно из предположений модели GARCH о том, что нормированные остатки нормально распределены.

Альтернативой в этом случае может служить явное предположение об ином виде распределения. При этом зачастую выбирают распределение Cтьюдента, поскольку при малых степенях свободы оно имеет большой куртозис. Часто распределение временных рядов является смещённым вправо. Для учёта этого обстоятельства следует использовать ассиметричные распределения с «тяжёлыми хвостами», которые описывают высокую вероятность больших скачков цен. Именно поэтому модели с таким распределением имеют явные преимущества перед классическими моделями (с нормальным распределением и распределением Стьюдента) в условиях нестабильности финансовых рынков.

Математические модели риска. Стоимостной мерой риска является величина, называемая VaR (Value-at-Risk). VaR даёт оценку величины, которую, с заданной доверительной вероятностью, не превысят ожидаемые в течение некоторого периода времени потери [9]. Согласно базельским документам, используется величина доверительного интервала 99 %, т. е. ожидаемые колебания цен с вероятностью 99 % не должны превышать установленной границы. VaR некоторой случайной величины X с заданной доверительной вероятностью η определяется следующим образом: VaR_n ( X ) = - inf { x e Rp ( X < x ) > n } , (0,01-квантиль).

Для того чтобы оценить эффективность различных математических моделей временных рядов для прогнозирования колебаний цен на акции, проанализируем величину VaR t _n ( y t ₊ ₁ ) , где ( y t ) t >о — временной ряд, описывающий дневное изменение цены на акцию. Он определяется

S следующим образом: y = log ——, где (^) — цена акции в момент времени t. Для моделиро-t -1- tt.

вания колебаний цен на акции использовались модель экспоненциально взвешенного скользящего среднего (ЕWMA — exponentially weighted moving average) и ARMA(1,1)-GARCH(1,1)-модель с различными типами распределений. В рамках EWMA-модели дневная волатильность определяется соотношением:

о 2 = Ло 2 - 1 ⁺( 1 - Л ) у^Л > 0. ⁽¹⁾База данных RiskMetrics, созданная Дж. П. Морганом (J. P. Morgan) в 1994 году для оценки суточной волатильности, использует модель EWMA с показателем Л = 0,94. Оказалось, что при таком выборе параметра λ предсказанные значения дисперсии широкого спектра рыночных показателей очень близки к реальным. Такое же значение параметра использовалось и для проведённых расчётов.

ARMA(1,1)-GARCH(1,1)-модель описывается следующими уравнениями: y t = ay t - 1 + ^bo t - 1 ^E t - 1 + ⁰ t ^E t + c , ⁰ 21 = ^a o + ^a i ° 2 1 - i ^E 2 1 — I + ^2 1 — I ,

где e0 = 0 и (et)— последовательность независимых и одинаково распределённых действи- тельных случайных величин; σt — стандартное отклонение; α, α0, α1, β1, b, c — параметры модели, которые подбираются, исходя из имеющихся наблюдений за некоторый временной период.

В дальнейшем будем называть ARMA-GARCH-модель (2) нормальной, если предполагается, что нормированные остатки ε _t имеют нормальное распределение. Если рассматривается распределение Стьюдента ( t -распределение) будем говорить о t -модели. Кроме этих двух широко используемых распределений исследуем также модель с CTS распределением (classical tempered stable distribution). Это так называемое распределение с «тяжёлыми хвостами». Нормированное CTS распределение задаётся следующей характеристической функцией [7]:

Ф X ( и ) = ф CTS ( и; а, Л + ,Л - ) = exp ( - иС Г ( 1 - а ) ( Л +^- ¹ - Л -^- ¹ ) + С Г ( - а ) ( ( Л + - iu ) ^а - Л + + ( Л - + iu ) ^а - Л - ) ) ,

С = (Г (2 - а)( Л+-2 + Ла-2 ))-1, с тремя параметрами а е (0,2) / {1}, Л +, Л- > 0.

ARMA-GARCH-модель (2) c таким распределением будем называть CTS моделью.

Целью исследований является сравнение эффективности моделей с различными видами распределений. Для краткости EWMA-модель (1) и модель (2) с нормальным распределением будем называть «нормальными» моделями, а модель с распределением Стьюдента и CTS-распределением будем называть «ненормальными» моделями. Временные ряды строились на основе эмпирических наблюдений для американской биржи S&P 500 и двух российских бирж ММВБ и РТС. Параметры моделей рассчитывались на основе ежедневных изменений курса, которые определялись по цене закрытия. Параметры «нормальных» моделей и модели c t -распределением находятся с помощью метода максимального правдоподобия. Для CTS-модели на первом шаге вычислялись параметры α₀, α₁, β₁, a , b , c для модели (2) с распределением Стьюдента, с помощью метода максимального правдоподобия, а на втором шаге определялся временной ряд y_t . Далее на основе полученных значений e _t подбирались параметры а, Л ₊ , Л _ для CTS распределения, используя метод максимального правдоподобия.

Для всех четырёх моделей (EWMA, нормальная ARMA-GARCH, t -ARMA-GARCH и CTS-ARMA-GARCH) были вычислены параметры временных рядов с 14 декабря 2004 года по 31 декабря 2008 года. Выбранные четыре года включают как низковолатильный (2005, 2006 год), так и высоковолатильный (2007, 2008 год) период, включающий в себя финансовый кризис в США 2008 года. Для каждого ежедневного прогноза изменения курса использовались наблюдения дневных курсов за 7 лет для S&P 500, ММВБ и РТС. На основе посчитанных значений y_t были определены значения VaR для рассмотренных четырёх моделей VaR_t _n ( y_t ₊ ₁ ) = - inf { % е Rp_t ( y_t ₊ ₁ < x ) > n } • Полученные результаты сравнивались с исследованиями, проведёнными Рачевым и Ким для американской биржи S&P 500 [7]. Сравнение показало качественное совпадение вычисленных значений параметров для всех рассмотренных моделей.

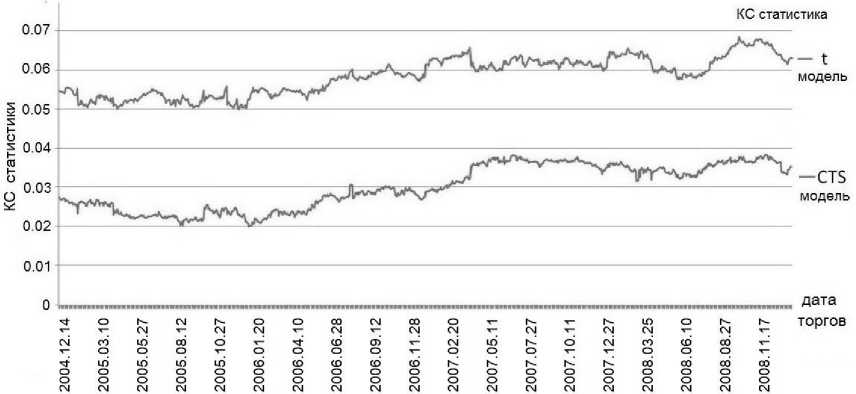
Рис. 1. КС статистика для биржи РТС

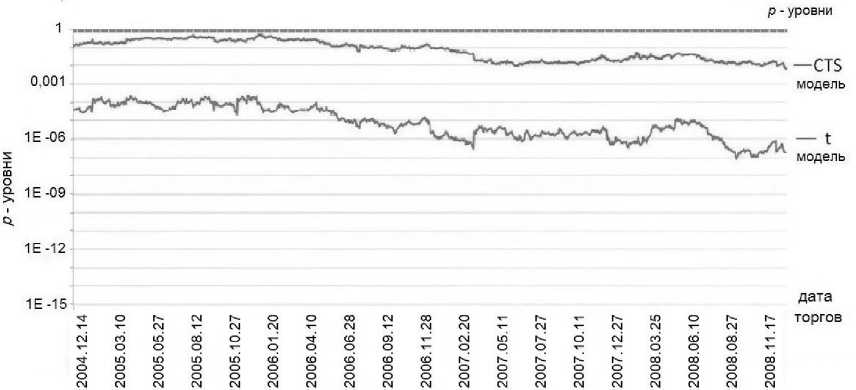
Рис. 2. р -уровни значимости для биржи РТС

Чтобы оценить точность прогнозирования VaR для рассмотренных моделей, было проведено тестирование с помощью критерия на правдоподобие Кристофферсона (CLR — Christoffersen’s Likelihood Ratio) [10]. Периоды для проведения тестирований были выбраны следующие:

• 1-годичный тест:

2005: с 14 декабря 2004 г. до 15 декабря 2005г.;

2006: с 16 декабря 2005 г. до 20 декабря 2006г.;

2007: с 21 декабря 2006 г. до 27 декабря 2007г.;

2008: с 28 декабря 2007 г. до 31 декабря 2008 г.;

• 2-годичный тест:

2005–2006: с 14 декабря 2004 г. до 20 декабря 2006 г.;

2007–2008: с 21 декабря 2006 г. до 31 декабря 2008 г.;

• 4-годичный тест:

2005–2008: с 14 декабря 2004 г. до 31 декабря 2008 г.

CLR-тест показывает суммарное количество ошибочных прогнозов значений VaR. Ошибочные прогнозы означают, что фактические потери превышают прогнозируемые. CLR-тест состоит из трёх частей: CLR-тест безусловного покрытия, CLR-тест независимости, совместный тест покрытия и независимости. В таблицах 1, 2 и 3 приводятся три CLR-статистики и соответствующие р-уровни значимости для VaRt 0 01 (yt+1) для четырёх рассмотренных моделей и различных перио- дов времени.

Таблица 1

Модель	1 год (255 дней)
Модель	2005 (14 дек. 2004 — 15 дек.					2005)		2006 (16 дек. 2005 — 20 дек. 2006)
	N	CLRuc	p	CLRind	p	CLRcc	p	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	2	0,219	0,719	0,031	0,858	0,161	0,922	4	0,710	0,399	0,128	0,720	0,838	0,657
Нормальная	0	5,125	0,023	X	x	x	x	3	0,075	0,782	0,071	0,788	0,147	0,928
t	0	5,125	0,023	X	x	x	x	2	0,129	0,719	0,031	0,858	0,161	0,922
CTS	0	5,125	0,023	X	x	x	x	2	0,129	0,719	0,031	0,858	0,161	0,922
Модель	1 год (255 дней)
Модель		2007 (21 дек.		2006 —	27 дек. 2007)				2008 (28 дек. 2007 —			31 дек. 2008)
	N	CLRuc	p	CLRind	p	CLRcc	p	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	10	12,651	0,000	0,819	0,365	13,471	0,001	7	5,316	0,021	0,396	0,528	5,713	0,057
Нормальная	8	7,512	0,006	0,520	0,470	8,032	0,018	9	9,966	0,001	0,661	0,416	10,628	0,004
t	2	0,129	0,719	0,031	0,858	0,161	0,922	3	0,075	0,782	0,071	0,788	0,147	0,928
CTS	4	0,710	0,399	0,128	0,720	0,838	0,657	3	0,075	0,782	0,071	0,788	0,147	0,928
Модель	2 года (510 дней)
Модель		2005—	2006 (14 дек. 2004		— 20 дек. 2006)				2007—	2008 (21 дек. 2006 — 31 дек. 2008)
	N	CLRuc	p	CLRind	p	CLRcc	p	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	6	0,151	0,696	0,143	0,705	0,295	0,862	17	17,417	0,000	1,175	0,278	18,592	0,001
Нормальная	3	1,025	0,311	0,035	0,850	1,060	0,588	17	17,417	0,000	1,175	0,278	18,592	0,001
t	2	2,474	0,115	0,015	0,900	2,490	0,287	5	0,002	0,964	0,099	0,752	0,101	0,950
CTS	2	2,474	0,115	0,015	0,900	2,490	0,287	7	0,640	0,423	0,195	0,658	0,835	0,658
Модель	4 года (1020 дней)
Модель		2005—	2008 (14 дек. 2004		— 31 дек. 2008)
	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	24	13,661	0,001	1,157	0,281	14,819	0,001
Нормальная	20	7,429	0,006	0,800	0,370	8,230	0,016
t	7	1,139	0,285	0,096	0,755	1,236	0,538
CTS	9	0,148	0,700	0,160	0,688	0,308	0,856

Проанализировав значения, содержащиеся в таблицах, можно сделать следующие выводы: количество ошибочных прогнозов N (1-й столбец в каждой таблице) для всех периодов значительно выше для моделей с нормальным распределением ошибок, что говорит об их неэффективности для прогнозирования значений VaR в предкризисное время.

CLR-тест безусловного покрытия (CLRuc — the CLR test of unconditional coverage) дал следующие результаты:

• 1-годичные тесты за 2005 и 2006 год и 2-годичный тест за 2005—2006 годы не отвергают все четыре модели на 1 % уровне значимости;
• 1-годичные тесты за 2007 и 2008 год, а также 2-годичный тест за 2007–2008 годы две «ненормальные» модели не отвергают, а две «нормальные» модели (EWMA- и нормальная-ARMA-GARCH-модель) отклоняют на 1 % уровне значимости для биржи S&P 500. Для российских бирж только одногодичный тест 2008 года отвергает нормальные модели;
• 4-годичный тест для биржи S&P 500 за 2005—2008 годы две «ненормальные» модели принимает, а две «нормальные» модели отклонены при р = 0,01.

CLR тест для биржи ММВБ

Таблица 2

Модель	1 год (255 дней)
Модель	2005 (14 дек. 2004 — 15 дек. 2005)							2006 (16 дек. 2005 — 20 дек. 2006)
	N	CLRuc	p	CLRind	p	CLRcc	p	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	3	0,090	0,763	0,072	0,787	0,163	0,921	4	0,745	0,388	0,129	0,718	0,874	0,645
Нормальная	2	0,112	0,737	0,032	0,857	0,144	0,930	4	0,745	0,388	0,129	0,718	0,874	0,645
t	0	5,045	0,024	x	x	x	x	1	1,200	0,273	0,008	0,928	1,208	0,546
CTS	0	5,045	0,024	x	x	x	x	1	1,200	0,273	0,008	0,928	1,208	0,546
Модель	1 год (255 дней)
Модель		2007 (21 дек. 2006			27 дек. 2007)				2008 (28 дек. 2007 —			31 дек. 2008)
	N	CLRuc	p	CLRind	p	CLRcc	p	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	2	0,125	0,723	0,031	0,858	0,157	0,924	8	7,555	0,006	0,522	0,469	8,078	0,017
Нормальная	2	0,125	0,723	0,031	0,858	0,157	0,924	11	15,614	0,000	1,000	0,317	16,614	0,000
t	1	1,225	0,268	0,007	0,929	1,233	0,539	5	1,876	0,170	0,201	0,653	2,078	0,353
CTS	1	1,225	0,268	0,007	0,929	1,233	0,539	5	1,876	0,170	0,201	0,653	2,078	0,353
Модель	2 года (510 дней)
Модель		2005—	2006 (14 дек. 2004 — 20 дек. 2006)						2007—	2008 (21 дек. 2006		— 31 дек. 2008)
	N	CLRuc	p	CLRind	p	CLRcc	p	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	7	0,694	0,404	0,198	0,656	0,892	0,640	10	3,873	0,049	0,407	0,523	4,280	0,117
Нормальная	6	0,178	0,673	0,145	0,703	0,323	0,850	13	8,908	0,002	0,692	0,405	9,601	0,008
t	1	4,861	0,027	0,004	0,949	4,865	0,087	6	0,181	0,669	0,145	0,702	0,327	0,849
CTS	1	4,861	0,027	0,004	0,949	4,865	0,087	6	0,181	0,669	0,145	0,702	0,327	0,849
Модель	4 года (1020 дней)
Модель		2005—	2008 (14 дек. 2004 — 31 дек. 2008)
	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	18	5,144	0,023	0,657	0,417	5,801	0,055
Нормальная	19	6,381	0,011	0,733	0,391	7,114	0,028
t	7	1,046	0,306	0,098	0,753	1,144	0,564
CTS	7	1,046	0,306	0,098	0,753	1,144	0,564

CLR-тест независимости (CLRind — the CLR test of independence) дал следующие результаты:

• все четыре модели не отвергаются на 1 % уровне значимости;
• две «ненормальные» модели не дают ошибочных прогнозов в 2005 году, поэтому невозможно выполнить тест на независимость. Это означает, что «ненормальные» модели могут переоценивать будущие убытки, что эквивалентно тому, что требуемый запас капитала будет больше, чем необходимо.

Совместный тест покрытия и независимости (CLRcc — the joint test of coverage and independence) дал следующие результаты:

• 1-годичный тест за 2008 год отвергает модель с нормальным распределением для всех трёх бирж;
• для биржи S&P 500 также отвергаются «нормальные» модели на основе 1-годичного теста за 2007 год, 2-годичного теста за 2007—2008 годы и 4-годичного теста за 2005—2008 годы.

Четыре 1-годичных периода можно разделить на две группы: первая — 2005 и 2006 годы и вторая — 2007 и 2008 годы. В 2005 и 2006 году рынок не был очень изменчивым и, как следствие, EWMA- и нормальная ARMA-GARCH-модель не отвергаются. Напротив, в 2007 и 2008 году рынок был неустойчивым и две «нормальные» модели были отвергнуты.

Таблица 3

CLR тест для биржи РТС

Модель	1 год (255 дней)
Модель	2005 (14 дек. 2004 — 15 дек. 2005)							2006 (16 дек. 2005 — 20 дек. 2006)
	N	CLRuc	p	CLRind	p	CLRcc	p	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	3	0,090	0,763	0,072	0,787	0,163	0,921	6	3,498	0,061	0,293	0,587	3,792	0,150
Нормальная	2	0,112	0,737	0,032	0,857	0,144	0,930	4	0,745	0,388	0,129	0,718	0,874	0,645
t	0	5,045	0,024	X	X	X	X	1	1,200	0,273	0,008	0,928	1,208	0,546
CTS	1	1,188	0,275	0,008	0,928	1,196	0,549	3	0,087	0,768	0,072	0,787	0,159	0,923
Модель	1 год (255 дней)
Модель		2007 (21 дек. 2006 —			27 дек. 2007)				2008 (28 дек. 2007 —			31 дек. 2008)
	N	CLRuc	p	CLRind	p	CLRcc	p	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	2	0,125	0,723	0,031	0,858	0,157	0,924	8	7,555	0,006	0,522	0,469	8,078	0,017
Нормальная	1	1,225	0,268	0,007	0,929	1,233	0,539	9	10,018	0,001	0,664	0,415	10,682	0,004
t	1	1,225	0,268	0,007	0,929	1,233	0,539	3	0,079	0,777	0,072	0,788	0,151	0,927
CTS	1	1,225	0,268	0,007	0,929	1,233	0,539	5	1,876	0,170	0,201	0,653	2,078	0,353
Модель	2 года (510 дней)
Модель		2005—	2006 (14 дек. 2004 — 20 дек. 2006)						2007—	2008 (21 дек. 2006		— 31 дек. 2008)
	N	CLRuc	p	CLRind	p	CLRcc	p	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	9	2,564	0,109	0,328	0,5666	2,892	0,235	10	3,873	0,049	0,407	0,523	4,280	0,117
Нормальная	6	0,178	0,673	0,145	0,703	0,323	0,850	10	3,873	0,049	0,407	0,523	4,280	0,117
t	1	4,861	0,027	0,004	0,949	4,865	0,087	4	0,225	0,635	0,064	0,799	0,289	0,865
CTS	4	0,229	0,632	0,064	0,799	0,293	0,863	6	0,181	0,669	0,145	0,702	0,327	0,849
Модель	4 года (1020 дней)
Модель		2005—	2008 (14 дек. 2004 — 31 дек. 2008)
	N	CLRuc	p	CLRind	p	CLRcc	p
EWMA	19	6,381	0,011	0,733	0,391	7,114	0,028
Нормальная	16	3,016	0,082	0,518	0,471	3,534	0,170
t	5	3,144	0,076	0,050	0,823	3,194	0,202
CTS	10	0,001	0,987	0,201	0,653	0,201	0,904

Сравнительный анализ рассмотренных моделей. Для всех четырёх периодов две «ненормальные» модели обычно имеют более высокие значения VaR , чем две «нормальные» модели. Для изучения этих различий проанализируем среднюю относительную разницу (ARD — the average of the relative difference) между VaR значениями для «нормальных» и «ненормальных» моделей. ARD вычисляется следующим образом:

ARD = E \/^D non - normal (х. \ \/aD normal / \ VaRt,0,01 (yt+1 ) VaR,o,oi (yt+1) _ VaR-™1 (yt+1) _ где VaRfOmll (yt+1) — значение VaR, основанное на одной из двух «нормальных» моделей;

VaR f^^- 1 ormal ( y t ₊₁ ) — значение VaR , основанное на одной из двух «ненормальных» моделей.

С практической точки зрения, ARD-значения связаны с расходами на управление рисками. Например, если менеджер использует «ненормальную» модель с ARD-значением, равным 30 % по сравнению с моделью EWMA, это означает, что этому менеджеру нужно на 30 % больше капитала, чем менеджеру, который использует модель EWMA. Следовательно, более низкое значение VaR является экономически более эффективным. Тем не менее, эти сбережения капитала в периоды стабильности на рынке могут иметь серьёзные последствия при падении рынка. Запас капи- тала, необходимый менеджеру, который использует «нормальную» модель, не может быть достаточным, чтобы покрыть убытки от падающего рынка. Даже если «ненормальные» модели могут быть неэффективными в период стабильности, они могли бы в значительной степени повысить надёжность инвестиций в случае коллапса на финансовых рынках.

Таблица 4 содержит ARD значения, вычисленные на основе двух «нормальных» моделей и двух «ненормальных» моделей для четырёх периодов. По сравнению с VaR -значениями для модели EWMA:

• t -ARMA-GARCH-модель обладает значением VaR за 2005 и 2006 год, большим на 32 % для S&P 500 и на 40 % для российских бирж;
• CTS-ARMA-GARCH-модель обладает примерно на 22 % большим VaR -значением за 2005 и 2006 год;
• t -ARMA-GARCH- и CTS-ARMA-GARCH-модель характеризуются VaR -значением за 2007 год, большим, соответственно, на 26 % и 16 % для S&P 500 и на 53 % и 32 % для российских бирж;
• t -ARMA-GARCH- и CTS-ARMA-GARCH-модель характеризуются VaR -значением за 2008 год, боль

По сравнению с VaR -значениями для нормальной ARMA-GARCH-модели:

• t -ARMA-GARCH-модель обладает значением VaR за 2005 и 2006 год, большим на 17 % для S&P 500 и на 34 % для российских бирж;
• CTS-ARMA-GARCH-модель характеризуется значением VaR за 2005 и 2006 год, на большим 7 % для S&P 500 и на 15 % для российских бирж;
• t -ARMA-GARCH- и CTS-ARMA-GARCH-модели характеризуются значением VaR за 2007 год, большим, соответственно, на 21 % и 10 % для S&P 500 и на 34 % и 16 % для российских бирж;
• t -ARMA-GARCH- и CTS-ARMA-GARCH-модели характеризуются значением VaR за 2008 год, боль

В таблице 4 CTS-ARMA-GARCH-модель имеет меньшие ARD-значения, чем t -ARMA-GARCH-модель.

Таблица 4

ARD значения

Индекс	«Нормальная» модель	«Ненормальная» модель	2005	2006	2007	2008
S&P 500	EWMA	t	0,3555	0,3199	0,2679	0,2358
S&P 500	EWMA	CTS	0,2349	0,2133	0,1620	0,1549
ММВБ	EWMA	t	0,4619	0,3994	0,5318	0,4040
ММВБ	EWMA	CTS	0,2664	0,2052	0,3325	0,2223
РТС	EWMA	t	0,4192	0,4037	0,5333	0,4593
РТС	EWMA	CTS	0,2376	0,2009	0,3167	0,2538

S&P 500	норм.	t	0,1719	0,1782	0,2152	0,2452
S&P 500	норм.	CTS	0,0708	0,0831	0,1070	0,1646
ММВБ	норм.	t	0,3577	0,3442	0,3489	0,3469
ММВБ	норм.	CTS	0,1757	0,1583	0,1733	0,1724
РТС	норм.	t	0,3085	0,3438	0,3433	0,3892
РТС	норм.	CTS	0,1413	0,1497	0,1535	0,1940

Заключение. Проведённые исследования свидетельствуют о том, что CTS-ARMA-GARCH-модель является самой устойчивой к колебаниям на рынке среди четырёх исследованных моделей по 12

трём причинам. Во-первых, KC-статистики для CTS-ARMA-GARCH-модели имеют более низкие значения, чем у t -ARMA-GARCH-модели за все четыре года исследований. Во-вторых, тест Кристофферсона отвергает две исследуемые «нормальные» модели для периодов неустойчивого рынка (2007 и 2008 гг.), a CTS-ARMA-GARCH-модель не отвергается тестом CLR как для низковолатильных периодов (2005 и 2006 гг.), так и для высоковолатильных периодов (2007 и 2008 гг.). В-третьих, с точки зрения двух «нормальных» моделей, CTS-ARMA-GARCH-модель имеет более низкие ARD-значения, чем t -ARMA-GARCH-модель. Проанализировав значения таблицы 4, можно заметить, что ARD-значения для всех периодов и моделей для американской биржи ниже, чем для российских бирж. Это говорит о том, что для обеспечения стабильности в кризисные периоды российским биржам нужны более высокие объёмы капитала.

Список литературы Моделирование биржевых колебаний в низковолатильные и высоковолатильные периоды

Engle, R. Autoregressive conditional heteroscedasticity with estimates of VaRiance of united kingdom inﬂation/R. Engle//Econometrica. -1982. -Vol. 50. -Pp. 987-1008.
Bollerslev, T. Generalized autoregressive conditional heteroskedasticity/T. Bollerslev//Journal of Econometrics. -1986. -Vol. 31. -No. 3. -Pp. 307-327.
Engle, R. F. What good is a volatility model?/R. F. Engle, A. Patton//Quantitative Finance. -2001. -Vol. 50. -Pp. 237-245.
Белоусов, С. M. Моделирование волатильности со скачками: применение к российскому и американскому фондовым рынкам/С. М. Белоусов//Квантиль. -2006. -№ 1. -C. 101-110.
Kim, Y. S. Tempered stable and tempered infinitely divisible GARCH models/Y. S. Kim et al.//Journal of Banking and Finance. -2010. -No. 34. -Pp. 2096-2109.
Kim, Y. S. The modified tempered stable distribution, GARCH-models and option pricing/Y. S. Kim et al.//Probability and Mathematical Statistics. -2009. -Vol. 29. -No. 1. -Pp. 91-117.
Kim, Y. S. Time series analysis for financial market meltdowns/Y. S. Kim et al.//Journal of Banking and Finance. -2011. -No. 35. -Pp. 1879-1891.
Bianchi, M. L. Tempered infinitely divisible distributions and processes/M. L. Bianchi et al.//Theory of Probability and Its Applications, Society for Industrial and Applied Mathematics. -2010. -Vol. 55. -No. 1. -Pp. 58-86.
Булдашев, С. В. Статистика для трейдеров/С. В. Булдашев. -Москва: Компания Спутник, 2003. -244 c.
Christoffersen, P. F. Evaluating interval forecasts/P. F. Christoffersen//International Economic Review. -1998. -Vol. 39. -No. 4. -Pp. 841-862.

Еще

Статья научная