Моделирование чрезвычайных ситуаций с применением почти-периодического анализа изображений структуры тайфунов

Тропические циклоны (тайфуны) представляют собой одно из самых разрушительных природных явлений, сопровождаемых ураганными ветрами и огромными океанскими волнами, катастрофическими ливнями и вызванными ими наводнениями, оползнями и селевыми потоками, которые наносят колоссальные разрушения объектам инфраструктуры и уносят тысячи человеческих жизней. Необходимо отметить, что, несмотря на уровень развития современных технологий, точность прогнозирования возникновения тропических циклонов и их эволюции недостаточно высокая и является предметом интенсивных исследований учеными разных стран. В связи с данными фактами прогнозирование тропических циклонов представляет собой важную и актуальную научную задачу, направленную на обеспечение гидрометеорологической безопасности населения и отраслей экономики страны. Современный анализ информации позволяет осуществлять трансформацию исходных наборов данных согласно выдвигаемым суждениям и гипотезам в целях упрощения выявления закономерностей и других сведений. Такими преобразованиями могут быть, например, растяжение или сжатие изображения, Фурье-преобразование, кодирование смысловой нагрузки текста в латентные контекстные векторы или смена системы координат. Среди система координат широко распространенной является прямоугольная декартова система координат, в которой возможно представить описание данных графического вида (например, фото и видео). Положение пикселя на изображении определяется координатами ширины и высоты, а цвет задаётся либо через яркость чёрно-белого оттенка в случае монохромного изображения, либо в виде комбинации яркостей трех или четырехцветных палитр RGB/CMYK.

Известно, что данные спутникового мониторинга тропических циклонов позволяют значительно расширить объем получаемой информации для подготовки объективного прогноза. Одна-

Математика

ко для анализа изображений, представляющих графический вид сферических объектов, например, таких, как тропические циклоны (тайфуны), необходимо учитывать циркулярный характер данных и применить к исходной информации преобразование в пространство полярных координат, выбрав в качестве центра построения радиус-векторов геометрический центр исследуемого объекта.

Основная часть

Преобразование изображения из прямоугольной системы координат в полярную проводится с применением тригонометрической функции арктангенса и выражения, известного как евклидова норма. Таким образом, система координат, описывающих положение пикселя с применением ширины и высоты, сменяется парой координат, задающих положение на основе длины радиус-вектора и угла отклонения радиус-вектора от нулевой оси согласно выражениям

р (x, y ) = J( Xc - x )2 +(Ус - у )2, Ө( x, y ) = arctan

У с ^- У x c - X

где x c , y_c - декартовы координаты центра преобразования; x , y - преобразуемые декартовы координаты пикселя; р , Ө - полярные координаты - длина радиус-вектора и угол.

Таким образом, изображение в декартовых координатах можно преобразовать в полярные координаты для дальнейшего анализа. Пример такого преобразования приведён ниже - исходное изображение представлено на рис. 1, а, красной точкой отмечен центр преобразования в полярные координаты, и на рис. 1, б приведено представление изображения в полярных координатах соответственно.

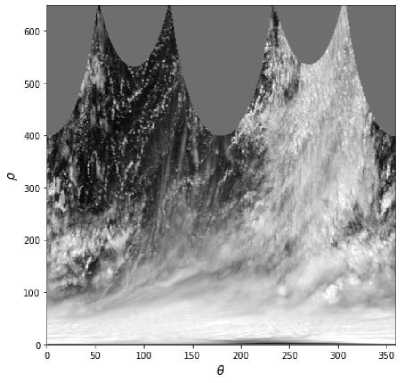
Рис. 1, б . Представление изображения тропического циклона в полярных координатах

Рис. 1, а . Исходное изображение тропического циклона и центр преобразования данных

Современный набор методов анализа данных имеет длинный список наименований, назначений и принципов работы. Среди прочих можно отдельно выделить методы почти-пери-одического анализа, в частности - метод, основанный на обобщённой сдвиговой функции [1,2].

Эффективность метода в различных задачах представлена в ряде работ. Так, в исследовании [1] приведены результаты сравнительного анализа предлагаемого метода с классическим методом Фурье-анализа, основанным на априорных периодических функциях. Следует отметить, что в работе [3] приведены результаты применения почти-периодического анализа на больших данных, представленные эмпирическими значениями замеров атмосферного давления. В экономической области были проведены работы по оценке биржевых [4] и макроэкономических [5] показателей.

Рассматриваемый метод опирается на процедуру разделения высокочастотных колебательных составляющих от низкочастотных трендовых динамик на основе теории пропорций и процесс извлечения почти-периодических характеристик на основе набора данных, лишённых тренда. В качестве независимого метода по разделению трендовой и колебательной составляющих используется метод, основанный на теории пропорций, позволяющий представить данные в координатах:

ln

y t -A t ' y t +А t

^yt ²

~ t ,

Парамонов А.А., Калач А.В.

где y_t - текущее значение; y_{t- д t} - предыдущее значение на расстоянии A t по аргументу; y_t +д _t - следующее значение на расстоянии A t по аргументу.

Полученные в результате разделения колебания затем анализируются на предмет наличия почти-периодов с учётом влияния параметра сдвига A t :

a ( т , A t ) =

n - т - 2A t

n -т- 2 A t z t = 1

In

^

y t -A t + т y t +A t- т

k

yL

-

In

(„         Л yt-At yt +At

k

yt    7

где n - общее число отсчётов функции y ( t ); т - почти-период.

Считая структуры данных подобными временным рядам, почти-периодический анализ можно применить по отношению к данным изображения по горизонтальным или вертикальным сре- зам в декартовой системе координат так же, как и к срезам по длине радиус-вектора в полярной системе координат. Так, для анализа по горизонтальному сечению изображения (см. рис. 1, а)

обобщённая сдвиговая функция имеет следующий срез (см. рис. 2).

" 0.75

0.50

0.00 ■

О 100     200     300     400     500     600     700

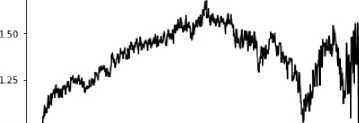
Рис. 2. Срез обобщённой сдвиговой функции Рис. 3. Срез обобщённой сдвиговой функции горизонтального сечения изображения с рис. 1, а вертикального сечения изображения с рис. 1, а

Срез показывает существование почти-периода в локальном минимуме вблизи значения в 600 пикселей. Также есть слабовыраженные локальные минимумы вблизи 100, 350 и 500 пикселей. При этом можно отметить систему малозначимых локальных минимумов в динамике кривой среза - иными словами, есть возможность определить менее значимые почти-периоды в других локальных минимумах, однако их существенность имеет меньший ранг.

Если провести почти-периодический анализ в отношении вертикального сечения изображения, то получится график, представленный на рис. 3.

Данный срез демонстрирует существенный локальный минимум в значении вблизи 900 пикселей, и также менее значимые вблизи 110, 260, 480, 640, 960 пикселей. Также видно, что существуют ещё менее значимые локальные минимумы.

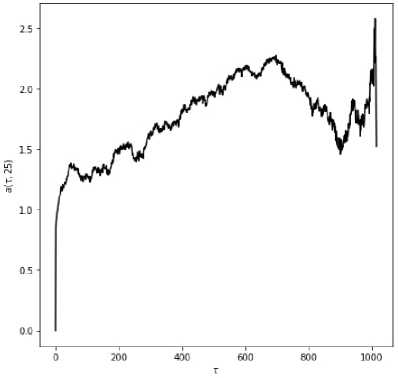
Рассмотрим применение почти-периодического анализа к вертикальному срезу изображения 2, б - соответствующего длине радиус-вектора в полярных координатах (рис. 4).

Срез на рис. 4 демонстрирует более гладкую кривую по отношению к результатам на рис. 2 и 3, что указывает на то, что столбцы преобразованного изображения больше соответствуют классу почти-периодических временных рядов. Также срез демонстрирует существенный локальный минимум вблизи 600 пикселей и менее существенные вблизи 100, 150, 400 пикселей. Значение почти-периода в 600 встречается также и в системе почти-периодов, связанных с горизонтальным сечением декартовых координат изображения, а также близко к величине 640 - одного из существенных почти-периодов вертикального сечения прямоугольной системы координат.

Анализ вышеприведённых сечений единообразен в отношении предположения отношения данных к структуре ряда с упорядоченным аргументом и представляющей собой некоторую последовательность, для которой одной из основных целей анализа является прогнозирование значения вне обозримого диапазона.

Математика

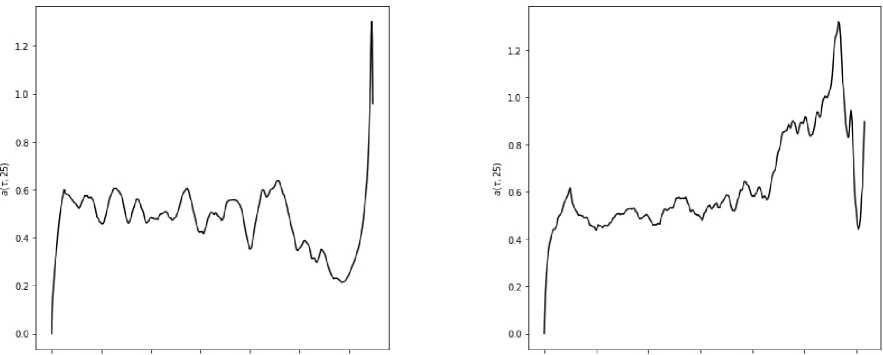
Рассмотрим аналогичное исследование в отношении углового (горизонтального) среза исследуемых данных в полярных координатах на интервале значений аргумента [0°; 359°] относительно данных с рис. 2 соответственно (рис. 5).

0 IDO 200      300      400      500      000                                    О 50       100       150       200       250       300

Рис. 4. Срез обобщённой сдвиговой функции верти- Рис. 5. Срез обобщённой сдвиговой функции горизон-кального сечения изображения с рис. 2 тального сечения изображения с рис. 1, б

Однако срезы изображения по угловой составляющей требуют отдельного внимания в отношении применения почти-периодического анализа. Данное суждение основывается на периодичности полярных координат – так, пиксель, находящийся в полярных координатах ( ρ , θ ), также находится и в положении ( ρ , θ + 360). Также при существовании углового почти-периода τ₁ должен существовать дополняющий почти-период τ ₂ = 360– τ ₁ согласно периодичности полярных координат.

Сравнение среза с его разворотом согласно тезису о существовании дополняющего периода представлено на рис. 6.

Установлено, что характер существования минимума совпадает, однако локальный минимум почти-периода в 260° не обладает убедительностью ввиду своего недостаточно малого значения. К тому же встаёт вопрос оценки соседнего значения в 240° относительно принадлежности его к классу значений почти-периодов. Если посмотреть на дополняющий почти-период (развернутый срез), то вертикально ниже почти-период находится ровно между ними – в 250°.

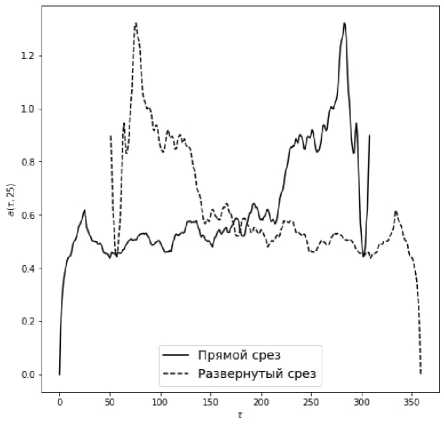
Рис. 6. Сравнение среза обобщённой сдвиговой функции с его отражением относительно 180°

Таким образом, возникает проблема несоответствия результатов набора данных естественной природе их описывающей шкалы.

В таком интервале не рассматривается периодическая связь между элементами, расположенными по разные стороны нулевой оси в порядке возрастания угла – так, например, мы не исследуем взаимосвязь между элементами на углах 250° и 13°.

Для решения этой проблемы предлагается рассмотреть расширенный угловой набор данных – исследовать интервал не [0°; 359°], а удвоенный интервал [0°; 719°]. В таком случае устанавливается взаимосвязь разделённых нулевой осью элементов, а также рассматриваются большие наборы для оценки дополняющих почти-периодов. Таким образом, новый набор данных примет следующий вид (рис. 7).

В таком случае почти-периодический анализ увеличивает временную нагрузку согласно описанной асимптотической оценке [6].

Парамонов А.А.,                        Моделирование чрезвычайных ситуаций с применением

Калач А.В.почти-периодического анализа изображений структуры тайфунов

Срез обобщённой сдвиговой функции для горизонтального сечения рис. 7 представлен на рис. 8.

ө

Рис. 7. Представление изображения в полярных координатах для углового интервала [0°; 719°]

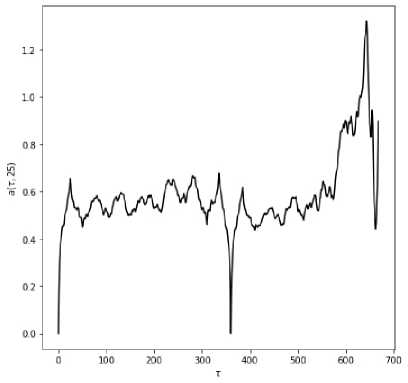
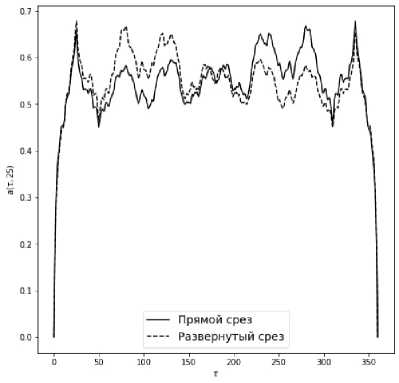
Рис. 8. Срез обобщённой сдвиговой функции горизон-    Рис. 9. График среза и разворота среза обобщенной тального сечения изображения с рис. 7          сдвиговой функции на исследуемом интервале данных

[0°; 360°]

Срез показал существование чистого периода в 360° – значение среза в данном аргументе равно 0. Также видна сильная корреляция внутри интервала [0°; 360°] для прямого значения среза и развёрнутой его последовательности (рис. 9).

Аналогичным образом возможно проверить воспроизведение почти-периодов, превышающих основные, имеющие значение до 180°, на 360° – то есть совпадение локальных минимумов на интервалах среза [0°; 360°] и [360°; 670°] соответственно. Результат проведенной проверки представлен на рис. 10.

Таким образом, установлено, что расширение диапазона угла позволяет качественно уточнить структуру угловых почти-периодов в системе полярных координат представления исходного изображения тропического циклона.

Необходимо отметить, что аналогичным образом возможно оценить эффект наращивания длины интервала – добавление ещё 360° – таким образом, получается 1080°. В таком случае срез обобщенной сдвиговой функции примет вид согласно рис. 11.

Установлено, что исследуемый срез обобщённой сдвиговой функции на интервалах [0°; 360°] и [360°; 720°] имеет практически идентичные значения. Повторение кривой среза на разных интервалах и инверсия этих интервалов носят идентичные характеры и близкие значения. Установлено, что последующее наращивание величины углового интервала качественно не изменило результата, закрепив структуру воспроизведением аналогичной системы почти-периодов на интервале [360°; 720°] градусов. Таким образом, сделан вывод об избыточности троекратного углового

Математика

интервала, но достаточности двукратного интервала при решении задачи выявления структурных особенностей тайфунов в полярных координатах с применением почти-периодического анализа путем обработки и анализе данных с упорядоченным аргументом в сложных условиях динамиче- ского изменения параметров тропических циклонов.

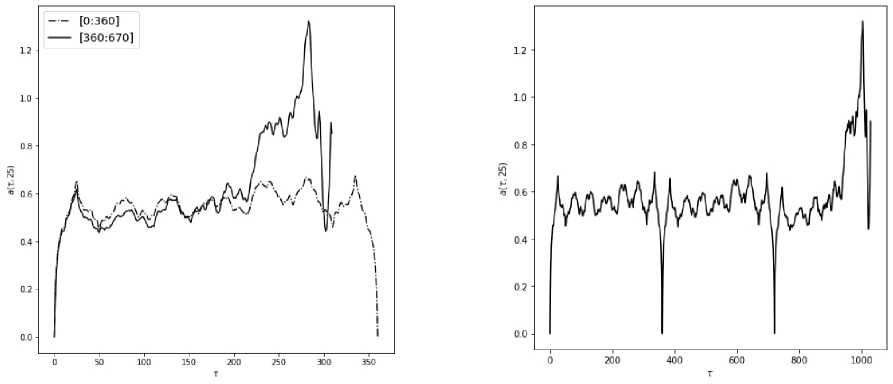
Рис. 11. Срез обобщённой сдвиговой функции углового среза для трехкратного кругового интервала

Рис. 10. График периодических интервалов среза обобщенной сдвиговой функции

Следует отметить, что вопросами использования современных вычислительных технологий обработки информации при человеко-машинном взаимодействии в сложных условиях успешно занимаются в научной школе профессора РАН Р.В. Мещерякова. Авторы выражают признательность за предоставленную возможность регулярного общения с Романом Валерьевичем Мещеряковым, поздравляют с юбилеем и желают успехов в научной деятельности.

Заключение

Исследование показало специфику применения почти-периодического анализа в полярной системе координат при обработке изображения тропического циклона. Сравнение срезов обобщенной сдвиговой функции, примененной к данным прямоугольной и полярной систем координат, показывает более гладкие, а как следствие, более естественные результаты во втором случае. Полярные координаты демонстрируют качественные результаты в обработке изображений круглых объектов. Исследование показало, что для получения наиболее точных результатов в значениях угловых почти-периодов необходимо рассмотрение расширенного, удвоенного интервала значения угла, если такое возможно в рамках источника данных. В таком случае увеличивается сила взаимосвязанных элементов, данных в полярных координатах на основе естественной периодичности цикличных (или круговых) данных, что позволяет провести полносвязный угловой анализ и сформировать полноценную систему оценочных почти-периодов, которая соответствует представлениям о дополняющих углах.

Полученные результаты могут быть использованы для визуализации данных из метеорологических центров, моделирования динамики развития чрезвычайных ситуаций, обусловленных активностью тропических циклонов, с целью обеспечения мероприятий и проведения аварийноспасательных и других неотложных работ.