МОДЕЛИРОВАНИЕ ЦИЛИНДРИЧЕСКИХ РАДИОЧАСТОТНЫХ ТРАНСПОРТИРУЮЩИХ КАНАЛОВ С ПОМОЩЬЮ АНАЛИТИЧЕСКИХ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ

ВВЕДЕНИЕ                ПСЕВДОПОТЕНЦИАЛЬНАЯ МОДЕЛЬ ДВИЖЕНИЯ

ИОНОВ В НЕЙТРАЛЬНОМ ГАЗЕ

Эта статья является прямым продолжением работы [1], в которой исследовались аналитические выражения для электрических потенциалов цилиндрических радиочастотных каналов для транспортировки заряженных частиц (ионов). В данной публикации с помощью псевдопотенци-альной модели движения заряженных частиц в высокочастотных электрических полях и аналитических выражений для электрических полей, полученных в предыдущей статье, исследуются особенности функционирования цилиндрических радиочастотных транспортирующих каналов. Рассматриваются двухфазная схема электрических напряжений на электродах, четырехфазная схема электрических напряжений на электродах, а также амплитудно-модулированные напряжения, обеспечивающие синхронную транспортировку заряженных частиц при помощи высокочастотного электрического поля типа А-волны. Исследование функционирования радиочастотных транспортирующих каналов с некруговыми и с мультиполь-но-сегментированными диафрагмами, рассмотренными в [1], осуществляется аналогичным образом и приводит к качественно идентичным результатам. При необходимости исследовать радиочастотные транспортирующие каналы нецилиндрической формы можно использовать аналитические выражения для электрических потенциалов из публикаций [2–4], однако анализ соответствующих моделей выходит за рамки данной статьи.

Для качественного описания движения заряженных частиц в высокочастотных электрических полях полезно использовать псевдопотенциаль-ную модель движения [5–25]. В соответствии с этой моделью движение заряженных частиц распадается на сумму "медленного" движения в некотором эффективном квазистационарном силовом поле и на высокочастотные осцилляции с маленькой амплитудой. При этом при движении заряженных частиц в среде нейтрального газа наблюдаются дополнительные эффекты, отсутствующие при движении в вакууме [2, 8, 19].

Рассмотрим движение ионов в высокочастотном электрическом поле, высокочастотный электрический потенциал которого имеет вид [19, 20]

U f ( x, y, z, t ) = U ^{( 0 )} ( x , y, z ) p 0 ( t ) +

+ M( P ^k ( t ) cos ( ^ k t ) ^{U (} ' ) ( x ^, У, z ) + k

+qk (t) sin (®kt) V(k)(x, y, z))], (1) где pk(t) и qk(t) — "медленные" функции времени, а ωk — "быстрые" круговые частоты высокочастотных напряжений, прикладываемых к электродам. Предполагается, что Vk: юк ~ ю (все частоты "быстрые"), Vk, j: |юк - Wj| ~ ю ("быстрые" частоты далеко отстоят друг от друга) и ωT ≫ 1, где ω — характерный масштаб "быстрых" частот, T — характерный масштаб времени для "медленного" движения ионов.

Выражение (1) является наиболее общим представлением для высокочастотных сигналов сложной формы и со сложным спектром, характеризующихся двумя различными масштабами времени и позволяющих применить псевдопотенциальную модель движения ионов. В [23] показано, что любое квазистатическое высокочастотное электрическое поле, у которого временной спектр распадается на узкие и далеко отстоящие друг от друга островки, можно привести к виду (1). Представление высокочастотного электрического поля в каноническом виде (1) является важным для получения корректной теории псевдопотенциала: например, при использовании формально эквивалентных математических выражений и эвристической технике усреднения уравнений движения можно легко получить вместо медленно меняющегося псевдопотенциала [7, p. 170], [17, 19–21] математически красивые, но физически неверные формулы [16, 17, 20, 25].

В соответствии с [26–29] эффект столкновений ионов с молекулами нейтрального газа можно заменить на эффективное вязкое трение по закону Стокса. Сила вязкого трения, пропорциональная скорости иона относительно неподвижного газа и по направлению противоположная к скорости иона, заменяет собой результат усредненных столкновений ионов с молекулами нейтрального газа при "протаскивании" ионов сквозь газ [26–

29]. Вместо коэффициента Стокса (представляющего собой, вообще говоря, теоретическую абстракцию и не имеющего прямого физического смысла), удобно использовать коэффициент подвижности ионов в нейтральном газе, который определяет связь между напряженностью постоянного электрического поля в рассматриваемой области пространства и установившейся скоростью равномерного движения ионов [26]. Коэффициент Стокса γ связан с подвижностью K соотношением γ = e / K , где e — это заряд иона.

В линейном приближении коэффициент Стокса не зависит от скорости ионов относительно неподвижного газа и определяется локальной температурой газа, локальным давлением газа и сечением столкновения ионов с молекулами нейтрального газа. Предполагается, что γ = γ ( x , y , z , t ) — это функция, медленно меняющаяся во времени и пространстве. В большинстве случаев вариант γ = const является вполне приемлемым для использования в разумной модели качественного движения ионов в нейтральном газе.

После аккуратной процедуры усреднения результирующих уравнений движения по времени в соответствии со схемой, использованной в [9, c. 119–123], [10–22], "медленное" движение ионов с массой m и зарядом e сводится к движению в псевдопотенциальном электрическом поле с "демпф и рованным" электрическим псевдопотенциалом U ( x , y , z , t ) . Этот псевдопотенциал задается формулой [6–8, 19]:

U(x , y , z , t ) = У              . ( p_k ² ( t ) Г( U< k ⁾ У + U ⁽ k ⁾ У + Uj k ⁾ У 1+ qjft) \ V V< k ⁾ У + ( v k ⁾ У + V ( k ⁾ У 11 ,     (2)

4m(o' + ®kk               x y              z' J kkk ;L' x y          z JJ, где для функций U(k)(x, y, z) и V(k)(x, y, z) нижние индексы x, y, z обозначают частные производные по соответствующим координатам, Ω = m / γ — параметр, имеющий смысл эффективной частоты столкновений ионов с молекулами нейтрального газа, γ — коэффициент Стокса для эффективной силы вязкого трения.

При отсутствии нейтрального газа Ω ≡ 0 и демпфированный псевдопотенциал (2) переходит в обычный псевдопотенциал [5–25]. С физической точки зрения псевдоэлектрическое поле, которое описывается градиентом электрического псевдопотенциала (2), обусловлено инерциально-стью движения ионов и наличием пространственного градиента амплитуды высокочастотного электрического поля. Никаких других псевдосил в правой части усредненных уравнений движения при движении ионов в вакууме не наблюдается.

Однако при наличии нейтрального газа и ненулевом пространственном градиенте фазы высоко- частотного электрического поля в правой части усредненных уравнений движения добавляется непотенциальное псевдоэлектрическое поле (далее — псевдополе либо псевдосила) с компонентами (EX, EY, EZ), обусловленное пространственным градиентом фазы высокочастотного электрического поля:

e    ^ t )

E x ( x , y , z , t ) = £            ⁷   P t ( t ) q t ( t ) x

t 2m (O + rnk)

_x ( U ^{( k )} V ^{( k )} - U ^{( k )} V ^{( k )} + U ^{( k )} v ^{( k )} - x xx        xx x         y xy

-U ^{( k} >p^{( k )} + г^{1k )}K^{( k )} - U^^{k )}K^{( k )} 1

xy y         z xz xz z ,           ( )

E Y ⁽ x , y , z , t ) = £ -^^I p- p_k ⁽ t ) Q k ⁽ t ^{) x}

x (u ^{( k} V ^{( k} ) _— U ^{( k} ) V ^{( k} ) + U ^{( k )} V ^{( k} ) _— x xy        xy x         y yy

• ( k ) ( k )         ( k ) ( k )         ( k ) ( k )

yy ^K y   ⁺ z г yz        yz г z ) ,

E Z ( x , y , ^z , t ) = £ y^y^r^p k p_k ( t ) Q k ( t ^{) x} k 2 m ( Q + ^_k )

• ( k )   ( k )         ( k )   ( k )         ( k )   ( k )

x    xz        xz   x          y    yz

—

ц ⁽ k )^( k ) ₊ ц⁽k)у⁽.k ) _ц⁽k)у(k )

yz + z г zz zz г z ). (5)

В отличие от псевдоэлектрического поля, соответствующего градиенту (точнее, антиградиенту) псевдопотенциала (2), не существует такой скалярной функции, градиентом которой может быть векторное поле ( E X , E Y , E Z ) .

Также в уравнениях "медленного" движения присутствует эффективная (усредненная)

вязкости с компонентами ( F X , F Y , F_Z ) :

сила

F_x ( x , y , z , t ) = — y ( x , y , z , t ) ( x ( t ) — U x ( x , y , z , t ) ) , F Y ( x , y , z , t ) = — Y ( x , y , z , t ) ( y ( t ) — и₇ ( x , y , z , t ) ) ,   (6)

Fz (x,y,z,t) = —Y(x,y,z,t)(z(t) — Uz (x,y,z,t)), где (ux, uY, uZ) — медленно меняющаяся во времени и пространстве скорость потока газа в окрестности рассматриваемой точки,

( x ( t ) , y ( t ) , z ( t )) — усредненная скорость движения иона в данный момент времени.

При наличии в формуле (1) ненулевого медленно меняющегося электрического потенциала U0(x, y, z, t) = U(0)(x, y, z) p0(t)     соответствующее электрическое поле также включается в правую часть уравнений "медленного" движения.

АНАЛИТИЧЕСКИЕ МОДЕЛИ

ВЫСОКОЧАСТОТНЫХ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ ЦИЛИНДРИЧЕСКИХ ТРАНСПОРТИРУЮЩИХ КАНАЛОВ

Предполагается, что для высокочастотного электрического поля справедлива квазистатическая модель электрического поля: в рассматриваемом ограниченном объеме высокочастотный электрический потенциал можно представить как произведение функции, которая описывает синхронное изменение во времени напряжений на электродах, и трехмерного электростатического потенциала, который соответствует постоянным электрическим напряжениям на электродах. Квазистатиче-ская модель применима, если характерное время изменения электрических напряжений на электродах много больше характерного времени распространения электрического возмущения в пределах устройства (т.е. длины устройства, деленной на скорость света).

Типичная конфигурация круговых диафрагм, которые используются в качестве электродов при создании цилиндрических транспортирующих каналов, показана на рис. 1.

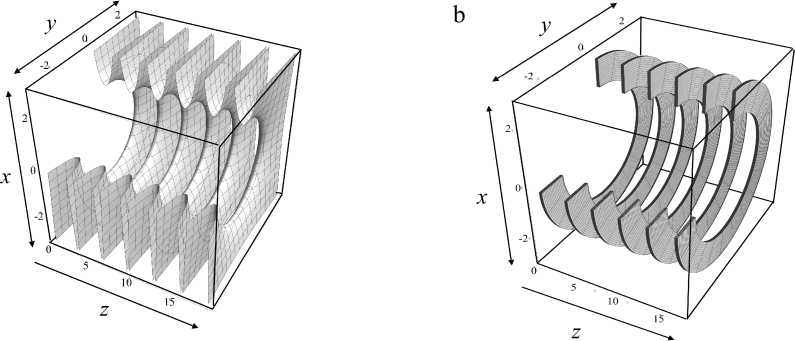
Рис. 1. Цилиндрический канал, состоящий из круговых диафрагм.

a — криволинейные электроды, соответствующие аналитическому электрическому потенциалу (7), (8);

b — упрощeнная система, состоящая из плоских круговых диафрагм конечной толщины.

Разрез показывает внутреннюю структуру электродов

Такие цилиндрические радиочастотные ловушки были предложены и успешно использовались для изоляции исследуемых ионов в [30–33]. См. также [5], [7, p. 165, 166].

Главная компонента электрического поля транспортирующих каналов, состоящих из тонких круговых диафрагм радиуса R, расположенных вдоль оси OZ с постоянным шагом L, к которым прикладываются электрические напряжения ±UR с чередующимися знаками, с хорошей точностью описывается формулами Герлиха [5], [7, 166]:

p. 165,

U C ⁽ z , r ^{) =} 1Rr ^{C0S( R}z ) I ° ^{( R}r ) ,

U s ⁽ z , r ) = tuR ^{sin ( R z} ) I 0 ^{( R r} ) ,

где U C — косинусоидальная форма, U S — синусоидальная форма, z , r — а ксиальная и радиальная координаты ( r = ^x ² + y ² ); UR — статические электрические напряжения, приложенные к диафрагмам; I 0 — модифицированная функция Бесселя нулевого порядка [34–36]; λ — параметр геометрического масштаба. Параметр λ = π / L , если ко всем диафрагмам прикладываются одинаковые электрические напряжения ± U_R с чередующимися знаками, и λ = π / (2 L ), если диафрагмы разбиты на четные и нечетные, причем к одним диафрагмам прикладываются электрические напряжения ± U_R , а для промежуточных (вспомогательных) диафрагм электрические напряжения равны нулю.

На оси симметрии r = 0 потенциал (7) ведет себя как U 0 cos( λz ), а потенциал (8) — как U 0 sin( λz ), где U 0 = U R / I 0 ( λR ) — амплитуда пространственных колебаний электростатического потенциала на оси системы. Чтобы создавать требуемые трехмерные электрические поля с электрическими потенциалами (7) либо (8), круговые диафрагмы с электрическими напряжениями ± U_R размещаются вдоль оси в точках локальных максимумов и минимумов осевого распределения электрического потенциала, а вспомогательные диафрагмы с нулевыми напряжениями (если они требуются) размещаются в точках, в которых осевое распределение обращается в ноль.

Расширенная система круговых диафрагм, снабженная диафрагмами с нулевыми напряжениями, оказывается одной и той же как для электрического потенциала (7), так и для электрического потенциала (8). Отличие состоит в том, какие именно электрические напряжения надлежит прикладывать к диафрагмам. Более того, в силу линейности уравнения Лапласа для линейной су- перпозиции электрических напряжений, по отдельности приложенных к четным и нечетным диафрагмам, будет создаваться электрическое поле с потенциалом, представляющим собой линейную суперпозицию потенциалов (7), (8) с нужными весовыми коэффициентами. Аналитические электростатические потенциалы (7), (8) оказываются полезным инструментом для конструирования аналитических моделей высокочастотного электрического поля при сложных конфигурациях радиочастотных напряжений на электродах, включая импульсные напряжения и напряжения со сложным спектром.

Наряду с основными компонентами (7), (8) в электрическом поле реальных цилиндрических каналов присутствуют также паразитные старшие пространственные гармоники электрического поля. Эти гармоники обусловлены отклонением реальной формы диафрагм от идеального криволинейного профиля, соответствующего точному аналитическому выражению (7), (8) для электрических потенциалов.

Аксиальные пространственные гармоники связаны с заменой диафрагм с криволинейным профилем на тонкие диафрагмы либо на диафрагмы конечной толщины. Азимутальные пространственные гармоники связаны с заменой мультиполь-ных диафрагм с идеальным мультипольным профилем на мультипольно-сегментированные круговые диафрагмы. Аксиальные и азимутальные старшие пространственные гармоники цилиндрических транспортирующих каналов подробно исследуются в [1].

Старшие пространственные гармоники электрического поля экспоненциально быстро затухают при удалении от края диафрагм, поэтому для оценки влияния возмущений электрического поля на функционирование цилиндрических транспортирующих каналов достаточно ограничиться первой ненулевой старшей гармоникой. В силу симметрии электродов и напряжений это будет синусоидальная либо косинусоидальная пространственная гармоника с номером 3 [1]. В результате электрические потенциалы возмущенного электрического поля имеют вид

^U C ( z , r >

® U ° [ cos ( Rz ) I ° ( Rr ) + s cos ( 3Rz ) I ° ( 3Rr ) ] ,     (9)

U S ( z , r ) =

= U ° [ sin ( Rz ) I ° ( Rr ) + s sin ( 3Rz ) I ° ( 3Rr ) ] ,   (1°)

где z, r — аксиальная и радиальная координаты (r = ^x2 + y2 ); U° — амплитуда колебаний осево- го распределения электрического потенциала; I0 — модифицированная функция Бесселя нулевого порядка [34–36]; λ — параметр геометрического масштаба, аналогичный параметру λ в формулах (7), (8); ε — относительный вклад третьей пространственной гармоники в осевое распределение электрического потенциала. Параметр ε зависит от толщины тонких диафрагм и безразмерного отношения R / L, где R — радиус круговых диафрагм, L — расстояние между соседними круговыми диафрагмами. При увеличении безразмерной величины R / L значение параметра ε быстро стремится к нулю, однако одновременно и амплитуда колебаний U0 = UR / I0(λR) осевого распределения электрического потенциала также стремится к нулю (если электрические напряжения ±UR, приложенные к электродам, не меняются при изменении параметра R / L).

ПСЕВДОПОТЕНЦИАЛЬНЫЕ МОДЕЛИ РАДИОЧАСТОТНЫХ КАНАЛОВ

Вводные замечания

Практическим примером использования аналитических потенциалов (7), (8) и (9), (10) могут служить радиочастотные электрические поля, используемые в ионно-оптических устройствах [5, 30–33, 37]. При анализе работы этих устройств движение заряженных частиц (ионов) удобно описывать с помощью псевдопотенциальной модели движения, которая вкратце описана в предыдущем разделе.

Псевдопотенциал с гофрировкой профиля

В классическом случае, когда на круговые диафрагмы подается высокочастотное синусоидаль- ное напряжение с фиксированной амплитудой и разностью фаз π между соседними диафрагмами [5, 8, 30–33], электрический потенциал высокочастотного электрического поля в середине канала транспортировки описывается формулой:

U ( z , r , t ) =

U        ( nz      ( nr A

= Т д П Ж)^cos [ T^{+ e} J ¹ " ^ T J ^{cos ( a t +} ^ ’ (11)

где z , r — аксиальная и радиальная координаты; U R , ω и φ — соответственно амплитуда, круговая частота и общий сдвиг фазы высокочастотных напряжений, прикладываемых к диафрагмам; I 0 — модифицированная функция Бесселя нулевого порядка; L — расстояние между соседними диафрагмами; R — радиус круговых диафрагм; параметр β задает смещение цепочки равномерно расположенных диафрагм относительно начала координат.

Псевдопотенциал, который описывает усредненное движение заряженных частиц с массой m и зарядом e в высокочастотных электрических полях (11) в вакууме, имеет вид

U ( z , r ) =

eπ      UR

2mL м [ 1 0 ( nR/L ) _J

x

xl sin²

Пz      A 22 ( nr 1       2 ( Пz      1 22

~ ^{+ e} I I о ГТ l ^{+ cos} ГТ ^{+ e} 1 1 1

L J \ L J \ L J

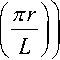
График функции (12) в нормированных безразмерных координатах показан на рис. 2.

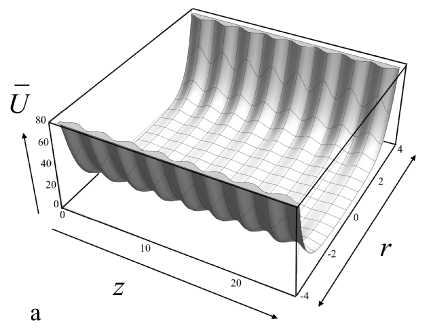
Рис. 2. Псевдопотенциал (12) в безразмерных нормированных координатах. а — трехмерный график в плоскости ( z , r ), b — гофрировка на оси r = 0

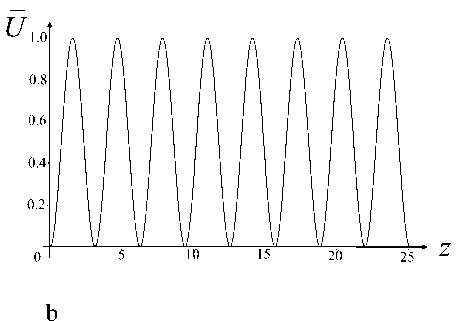
Псевдопотенциал (12) не меняется во времени и представляет собой гофрированный желоб, обеспечивающий удержание заряженных частиц в окрестности оси системы (рис. 2, a). Отметим, что заметная гофрировка сохраняется на оси системы r = 0 (рис. 2, b). Это означает, что за исключением отдельных точек, в которых псевдопотенциал обращается в ноль, на оси присутствует ненулевое высокочастотное электрическое поле. Впрочем, при R ≥ 4 L это поле пренебрежимо мало в силу экспоненциального роста множителя I 0 ( πR / L ) в знаменателе формулы (11).

При движении в газе демпфированный псевдопотенциал (2) отличается от выражения (12) наличием постоянного демпфирующего множителя ω ² / ( ω ² + Ω²). Фаза высокочастотного электрического поля (11) одинакова в любой точке пространства, поэтому непотенциальное псевдоэлек-трическое поле (3)–(5) отсутствует. Кроме того, за счет вязкого трения (6) ионы быстро теряют начальную кинетическую энергию и в конечном счете оказываются на оси транспортирующего канала в локальных минимумах осевой гофрировки псевдопотенциала, в которых высокочастотное электрическое поле отсутствует.

Электрический потенциал высокочастотного электрического поля (11), к которому добавлены возмущающие пространственные гармоники (9), (10), описывается формулой

U ( z , r , t ) = U 0 X

X

( nz ~ I cos IL + в) 10

x cos (at + у ) ,

( 3nz , _ I_T + s cos I — + 3в 1 10

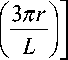
X

где U 0 — амплитуда колебаний электрического потенциала на оси системы, ε — относительный вклад третьей пространственной гармоники в электрическое поле на оси по сравнению с первой пространственной гармоникой, а остальные параметры в формуле (13) совпадают с аналогичными параметрами формулы (11).

Псевдопотенциал, который описывает усредненное движение заряженных частиц с массой m и зарядом e в высокочастотных электрических полях (13) в вакууме, имеет вид

U ( z , r ) =

eπ ² U ₀ ²

2 mL ² ω ²

. 2 I nz    _ I r2 I nr I       2 I nz    _ I r2 I nr II

sin--+ в In — + cos--+ в I — +

l L J 0 I L J I L J 1 I L J)

. I • I nz , I 3nz .    \ (nr V (3nr I ,

+ 6 s sin -- + в sin --- + 3в I n -- 4 --- +

l l L J l L J 01 L J ч L J

(nz    I    (3nz     I (nr\

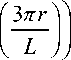
+ cos I — + в I cos I — + 3в 111    11

l L     J    l L       J ч L J 1

+ 9 s²

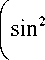
3nz i_n}_T2 — + 3в I I 02 L J

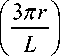
+ cos

3p+зв I i;

График функции (14) в нормированных безразмерных координатах показан на рис. 3. Наличие дополнительных пространственных гармоник приводит к более резкому росту стенок псевдопо-тенциального желоба при приближении к краям круговых диафрагм (рис. 3, а), а также усложняет профиль гофрировки псевдопотенциала (рис. 3, b). В итоге возрастает наклон стенок локальных ловушек в точках оси, соответствующих нулевому высокочастотному электрическому полю, уменьшается значение псевдопотенциала в точках локальных максимумов, а также появляются дополнительные локальные ловушки небольшой глубины в прежних точках максимума осевого распределения псевдопотенциала (рис. 3, b). В результате в центральной области транспортирующего канала образуется сложная структура локальных псевдо-потенциальных ловушек, в которых могут задерживаться заряженные частицы в процессе их изоляции и транспортировки.

В присутствии нейтрального газа псевдопотенциал (14) заменяется на демпфированный псевдопотенциал, который отличается от выражения (14) наличием постоянного демпфирующего множителя ω ² / ( ω ² + Ω²). Фаза высокочастотного электрического поля (13) одинакова в любой точке пространства, поэтому псевдосила (3)–(5) равна нулю во всех точках пространства точно так же, как и при отсутствии возмущений в виде старших пространственных гармоник.

a

b

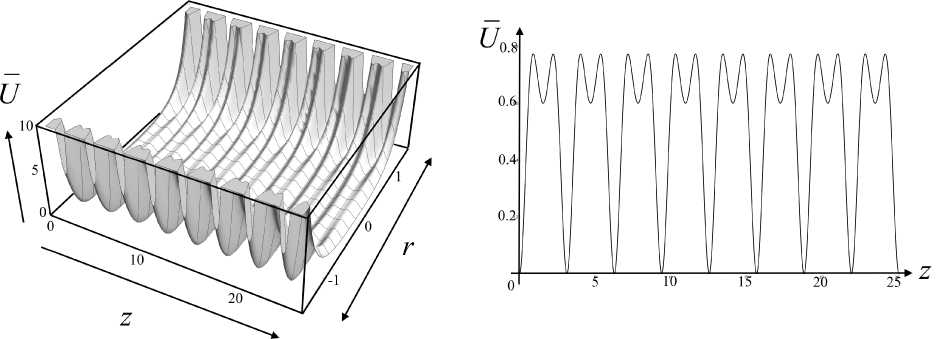
Рис. 3. Псевдопотенциал (14) в безразмерных нормированных координатах. а — трехмерный график в плоскости ( z , r ), b — гофрировка на оси r = 0

За счет вязкого трения (6) ионы быстро теряют начальную кинетическую энергию, а в конечном счете оказываются на оси транспортирующего канала в локальных минимумах гофрировки псевдопотенциала. Однако теперь заряженные частицы могут накапливаться также в дополнительных локальных ловушках не слишком большой глубины, которые появляются на вершинах прежних максимумов осевого распределения псевдопотенциала (рис. 3, b) по причине наличия старших пространственных гармоник высокочастотного электрического поля.

Псевдопотенциал с гладким профилем

Рассмотрим вариант, когда на круговые диафрагмы подается высокочастотное синусоидальное напряжение с фиксированной амплитудой и разностью фаз π / 2 между соседними диафрагмами [37]. В этом случае электрический потенциал высокочастотного электрического поля в середине канала транспортировки описывается формулой

U ( z, r, t ) =

Un       (Пz „\_т П nr A

= ; R ---- cos + в Il       cos ( ®t + Q l +

1 0 (nR/ 2 L )    L 2 L    J 0 1 2 L J

U ( nz        nr Л

⁺ IJmE) sin L 2 L^+в J ¹ 0 L 2 L J sin ( “t ⁺^ ⁽¹⁵⁾

Параметры в формуле (15) совпадают с аналогичными параметрами формулы (11).

Псевдопотенциал, который описывает усредненное движение заряженных частиц с массой m и зарядом e в высокочастотных электрических полях (15) в вакууме, имеет вид

U ( z, r ) = eπ2 8mL2ω2

___UR

L 1 о ( nR/ 2 L ) J

nr 1 r2| nr \ \

¹ 4 2 L )^{+ 1} 4 tl JJ .⁽¹⁶⁾

При движении в газе демпфированный псевдопотенциал (2) отличается от выражения (16) наличием постоянного демпфирующего множителя ω ² / ( ω ² + Ω ). Кроме того, за счет вязкого трения (6) ионы быстро теряют начальную кинетическую энергию и в конечном счете оказываются на оси транспортирующего канала.

График функции (16) в нормированных безразмерных координатах показан на рис. 4. Псевдопотенциал (16) не меняется во времени и представляет собой гладкий желоб, обеспечивающий удержание заряженных частиц в окрестности оси системы (рис. 4). Тот факт, что псевдопотенциал (16) не зависит от координаты z , означает, что в вакууме в любой точке пространства усредненное псевдопотенциальное воздействие на заряженные частицы в аксиальном направлении у высокочастотного электрического поля (15) отсутствует.

Хотя при r = 0 псевдопотенциал (16) и является константой (и, соответственно, обусловленная псевдопотенциалом напряженность электрического псевдополя равна нулю), но сам по себе он не равен нулю (рис. 4, b). Это означает, что на оси присутствует ненулевое высокочастотное электрическое поле, которое раскачивает заряженные a                                       b

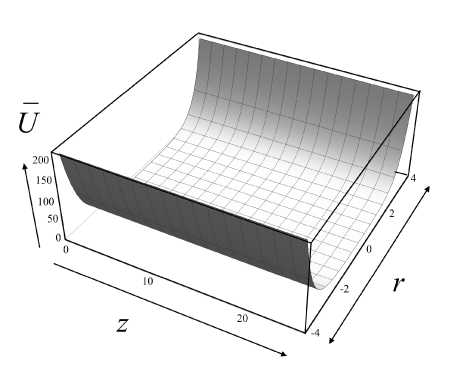
Рис. 4. Псевдопотенциал (1 6) в безразмерных нормированных координатах.

а — трехмерный график U ( z , r ) в плоскости ( z , r ), b — график зависимости U ( r ) вдоль линии z = 0

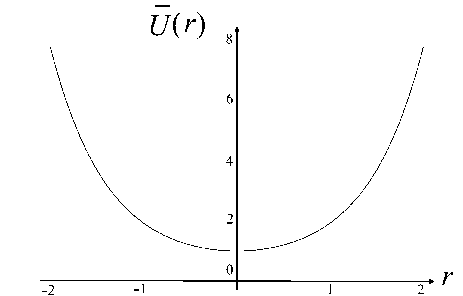
частицы, никуда их не перемещая. При R ≥ 4 L это поле пренебрежимо мало в силу экспоненциального роста множителя I 0 ( πR / 2 L ) в знаменателе формулы (15).

У высокочастотного электрического поля (16) фаза в разных точках пространства разная. Поэтому наряду с псевдоэлектрическим полем, которое представляет собой градиент псевдопотенциала (16) с демпфирующим множителем, также присутствует ненулевая псевдосила, которая в соответствии с формулами (3)–(5) имеет вид:

E X = 0, E Y = 0,

E = п (о/ ^)

Z 16 mL ( О ² + ю ² )^Х

I 1 0 ( nR / 2 L ) J

f     UR    '

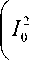
+ 1 22

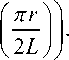
Если поменять сдвиг фазы высокочастотного напряжения между соседними диафрагмами с +π / 2 на –π / 2, то знак компоненты EZ электри- ческой псевдосилы поменяется на противоположный. Как это следует из сравнения формул (16) и (17), графики для псевдосилы eEZ совпадают с рис. 4 за исключением масштабирующего множителя. На оси системы при R ≥ 4L тянущая либо тормозящая непотенциальная псевдосила eEZ пренебрежимо мала.

Направленная вдоль оси OZ псевдосила eE_Z квадратична вблизи оси и экспоненциально растет при заметном удалении от оси. Она осуществляет перемещение заряженных частиц по осевому направлению в ту или иную сторону в зависимости от сдвига фазы высокочастотных напряжений между соседними электродами независимо от знака заряда заряженных частиц. Любопытно, что направленная вдоль оси псевдосила не зависит от координаты z , хотя заметно меняется с изменением координаты r .

Электрический потенциал высокочастотного электрического поля (15), к которому добавлены возмущающие пространственные гармоники (9), (10), описывается формулой

U ( z , r , t ) = U 0

^{+ U} 0

I п z    L cos + в In

1 2 L    J ⁰

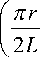
f 3 пz

+ s cos +

I 2 L

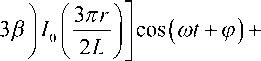
• I п z       \_T

Sin + в I

1 2 L    J ⁰

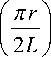
. f 3 пz

+ Sin +

I 2 L

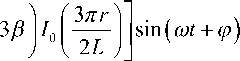
где U0 – амплитуда колебаний электрического по- третьей пространственной гармоники в электриче-тенциала на оси системы, ε – относительный вклад ское поле на оси по сравнению с первой простран- ственной гармоникой, а остальные параметры в формуле (18) совпадают с аналогичными параметрами формулы (11).

Псевдопотенциал, который описывает усредненное движение заряженных частиц с массой m и зарядом e в высокочастотных электрических полях (18) в вакууме, имеет вид

U (z, r ) =

eπ ² U ₀ ²

8 mL ² ω ²

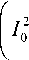
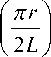
+ 1 12

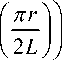
+ 9s ²

^п ^ ₊ 1=

2 L J    ¹

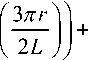
πz

+ 6 e cos — +

I L

I 0 ²

2в  I о

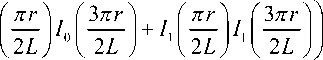
График функции (19) в нормированных безразмерных координатах показан на рис. 5. Наглядно видно, что наличие дополнительных пространственных гармоник приводит к появлению гофрировки у гладкого псевдопотенциального желоба, стенки которого по-прежнему растут по экспоненциальному закону при приближении к краям круговых диафрагм. В итоге в окрестности оси OZ появляются дополнительные локальные ловушки, в которых могут задерживаться заряженные частицы в процессе их изоляции и транспортировки. Следует отметить, что минимальное значение псевдопотенциала на оси OZ по-прежнему положительно, что означает, что высокочастотное электрическое поле отлично от нуля во всех точках оси OZ , включая локальные минимумы псевдопотенциала на оси.

В присутствии нейтрального газа псевдопотенциал (19) заменяется на демпфированный псевдопотенциал, который отличается от выражения (19) наличием постоянного демпфирующего множителя ω ² / ( ω ² + Ω²). За счет вязкого трения (6) ионы быстро теряют начальную кинетическую энергию, а в конечном счете оказываются на оси транспортирующего канала в локальных минимумах паразитной гофрировки псевдопотенциала, появившейся из-за наличия старших пространственных гармоник у высокочастотного электрического поля.

Присутствие старших пространственных гармоник также сказывается на поведении псевдосилы, обусловленной пространственным градиентом фазы высокочастотного электрического поля и наличием вязкого трения при движении в нейтральном газе:

b

a

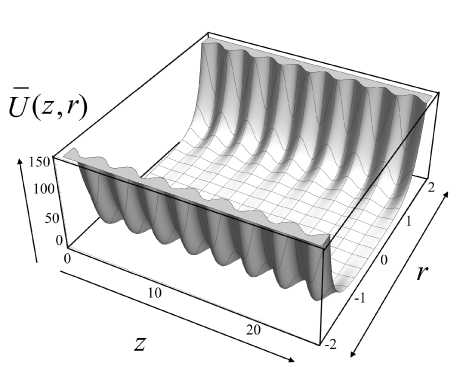
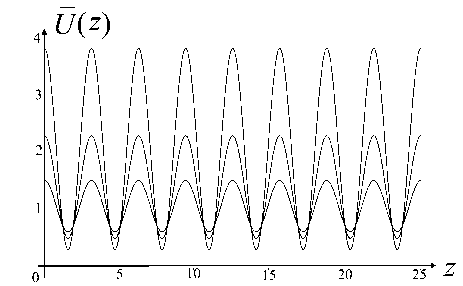
Рис. 5. Псевдопотенциал (19) в безразмерных нормированных координатах.

а — трехмерный график в плоскости ( z , r ), b — гофрировка вдоль оси OZ при нескольких разных значениях r = const

E .

—

\Zz

ЗеПи0 (Q/a) 8mL(Q0 + a2)

■ I n z , £ Sin +

I L

0в )

I 0

nr IJ 3nr I  r ( 3nr 11 П nr

I + II

2 L ) ¹ V 2 L )     ⁰ V 2 L ) ¹ V 2 L

еПи0 (Q/a) 16mL (Q2 + a2)

I

V

+ 1 1 ²

nr I

2 L ))

+ 27 _S²\I o ²

I—\ I°

V 2 L )    ¹

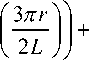
I n z + 12 f cos +

V L

2в )| I o

nr If 3nr I ( nr If 3nr

I + 1 I

2 L ) ⁰ V 2 L )   ¹ V 2 L ) ¹ V 2 L

На рис. 6 и рис. 7 показаны графики псевдосилы (20). Из рисунков видно, что из-за появления старших пространственных гармоник в разложении высокочастотного электрического поля у аксиальной компоненты псевдосилы eEZ появляется гофрировка (рис. 6), а радиальная компонента псевдосилы eEZ перестает быть нулем, демонстрируя

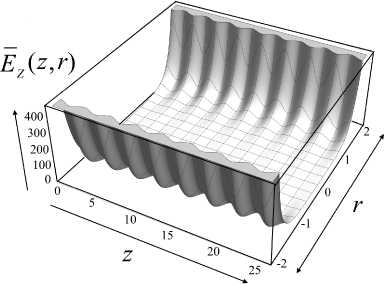
Рис. 6. Аксиальная компонента eE_Z псевдосилы (20) в безразмерных нормированных координатах.

а — трехмерный график в плоскости ( z , r ), b — гофрировка вдоль оси OZ при разных значениях r = const

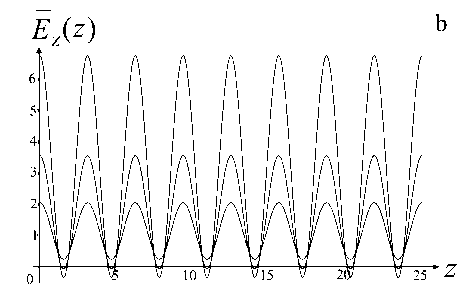
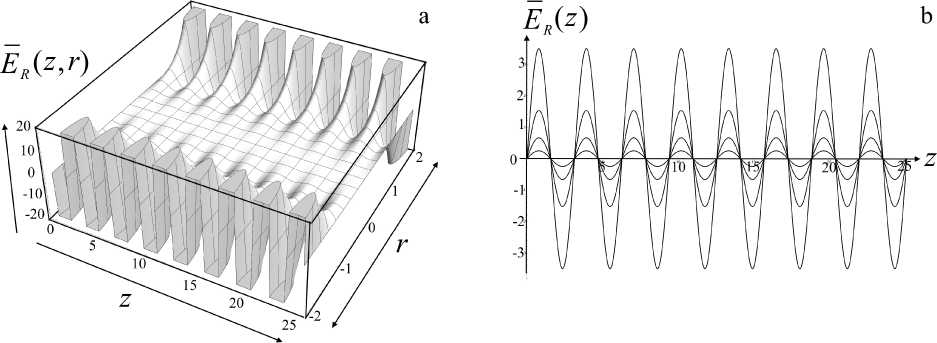
Рис. 7. Радиальная компонента eE_R псевдосилы (20) в безразмерных нормированных координатах.

а — трехмерный график в плоскости ( z , r ), b — осцилляции при смещении вдоль оси OZ при разных значениях r = const

пространственные осцилляции с периодическим изменением знака по мере перемещения вдоль оси OZ (рис. 7). Амплитуда пространственных осцилляций для обеих компонент псевдосилы экспоненциально растет по мере приближения к краям диафрагм. Как и должно быть, исходя из соображений симметрии, при приближении к оси OZ радиальная компонента псевдосилы ER стремится к нулю в соответствии с формулой (17), а при удалении от оси OZ обе компоненты E и E экспо-RZ ненциально растут. Интересно, что по мере удаления от оси OZ паразитные пространственные осцилляции аксиальной компоненты EZ могут настолько возрастать, что она начинает менять знак в некоторых точках.

Если поменять сдвиг фазы высокочастотного напряжения между соседними диафрагма м и с + π / 2 на – π / 2, то знаки компонент E и E RZ электрической псевдосилы поменяются на противоположные. Вблизи оси системы при R ≥ 4 L обе компоненты псевдосилы (20) пренебрежимо малы.

муле (21) совпадают с аналогичными параметрами формулы (11).

Псевдопотенциал, который описывает усредненное движение заряженных частиц с массой m и зарядом e в высокочастотных электрических полях (21) в вакууме, имеет вид

U ( z , r , t ) =

eπ ²

___UR

8 mL²m ² ^ 1 ₀ ( nR/ 2 L )

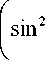
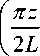
у X

— Q t + в - V 112

+

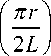
+ cos

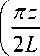
— Q t + в - V 112

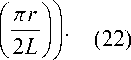
Псевдопотенциал с эффектом А-волны

Система круговых диафрагм может использоваться для принудительной транспортировки заряженных частиц высокочастотным электрическим полем (принцип А-волны [8, 24, 38–41]). Здесь на круговые диафрагмы подается высокочастотное синусоидальное напряжение со 100% амплитудной модуляцией, осуществляемой по синусоидальному закону со сдвигом фаз амплитудной модуляции π / 2 между соседними диафрагмами. Электрический потенциал высокочастотного электрического поля в середине канала транспортировки описывается формулой

U ( z , r , t ) =

U R

1 0 ( nR/ 2 L )

I nz _n cos — + в

[ 2 L

X

+

^x I 0

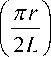
cos (Qt + v) cos (mt + ф) +

U R

1 0 ( nR/ 2 L )

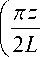
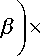
X I ₀

sin (Qt + v) cos (mt + ф)

где Ω — круговая частота синусоидальной амплитудной модуляции высокочастотных напряжений, ψ — общий сдвиг фазы синусоидальной амплитудной модуляции, а остальные параметры в фор-

При движении в газе демпфированный псевдопотенциал (2) отличается от выражения (22) наличием постоянного демпфирующего множителя ω ² / ( ω ² + Ω²). Фаза высокочастотного электрического поля (21) одинакова в любой точке пространства, поэтому непотенциальное псевдоэлек-трическое поле (3)–(5) отсутствует. Кроме того, за счет вязкого трения (6) ионы быстро теряют начальную кинетическую энергию и поэтому в конечном счете оказываются на оси транспортирующего канала в локальных медленно перемещающихся минимумах осевой гофрировки псевдопотенциала (см. рис. 8), в которых высокочастотное электрическое поле отсутствует.

График функции (22) в нормированных безразмерных координатах показан на рис. 8. Псевдопотенциал (16) меняется во времени и представляет собой постепенно смещающийся вдоль оси OZ гофрированный желоб, совпадающий по форме с псевдопотенциалом (12) (рис. 8, a). Как и псевдопотенциал (12), он обеспечивает удержание заряженных частиц в окрестности оси системы.

Если отношение радиуса диафрагм к расстоянию между соседними диафрагмами лежит в диапазоне R / L e [1.5, 2.5] (см. публикацию [1]), то на оси системы образуется синусоидальная волна псевдопотенциала, перемещающаяся вдоль оси OZ со скоростью, контролируемой частотой амплитудной модуляции Ω (рис. 8, b). В ее минимумах (локальных радиочастотных ловушках) концентрируются заряженные частицы с разными массами и зарядами, которые вследствие этого принудительным образом перемещаются синхронно с бегущей волной псевдопотенциала с единой групповой скоростью, контролируемой однозначным образом с помощью закона изменения электрических напряжений на электродах.

b

a

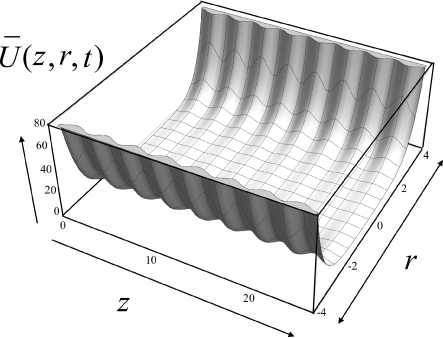
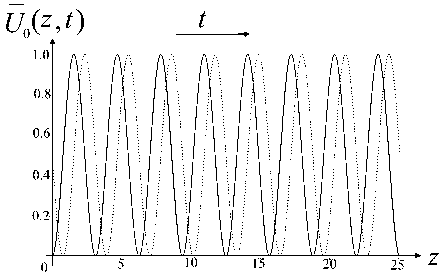
Рис. 8. Псевдопотенциал (22) в безразмерных нормированных координатах.

а — трехмерный график в плоскости ( z , r ) в некоторый момент времени, b — значение на оси r = 0 для двух разных моментов времени

a                                            b

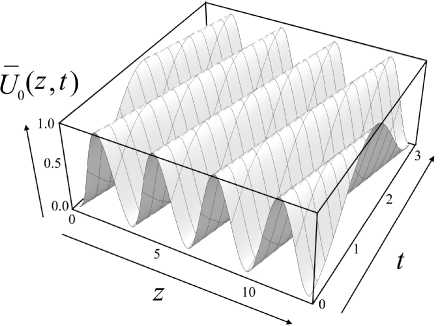
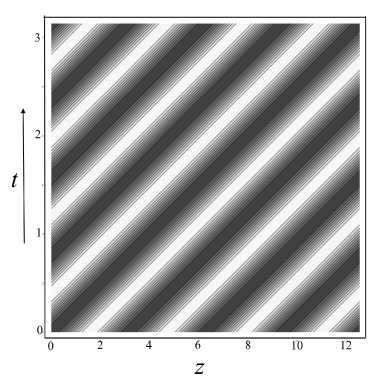
Рис. 9. Транспортировка заряженных частиц вдоль оси r = 0 с помощью бегущей волны псевдопотенциала (22) (эффект А-волны).

а — трехмерный график на плоскости ( z , t ) для транспортирующего псевдопотенциала U ( z , r , t )) = U 0 ( _z , t ) , b — карта на плоскости ( z , t ) для эквипотенциальных линий транспортирующего псевдопотенциала U ₀ ( z , t )

Транспортировку заряженных частиц с помощью эффекта А-волны можно проиллюстрировать следующим образом (рис. 9). Рассмотрим движение заряженных частиц, расположенных непосредственно на оси r = 0, под воздействием псевдопотенциала U0 (z, t) = U (z, r, t )| . Псевдопотенциал U (z, r, t) квадратично растет при удале- нии от оси, а на самой оси достигает минимума, так что заряженные частицы надежно удерживаются в окрестности оси высокочастотным электрическим полем. Поскольку псевдопотенциал высокочастотного электрического поля меняется во времени медленно (с точки зрения масштаба быстрых осцилляций высокочастотного электрического поля), то заряженные частицы успевают прийти в состояние равновесия и сконцентрироваться в локальных минимумах функции U0 (z, t). При адиабатическом смещении локальных минимумов псевдопотенциала заряженные частицы, захваченные этими локальными псевдопотенци-альными ловушками, перемещаются синхронно с перемещениями указанных минимумов.

Хотя колебания заряженных частиц внутри локальных ловушек сугубо индивидуальны и зависят от масс, зарядов и текущих кинетических энергий заряженных частиц, но поступательное движение группы заряженных частиц как единого целого однозначным образом определяется перемещениями вдоль оси локальных минимумов волны псевдопотенциала U 0 ( z , t ) . На рис. 9, b, в виде темных полос показаны непрерывные "дорожки", составленные из локальных минимумов псевдопотенциала U 0 ( z , t ) , вдоль которых происходит "выдавливание" заряженных частиц стенками псевдопотенциальных ловушек по мере увеличения времени t и смещения на рис. 9, b, сечения t = const в вертикальном направлении.

Весь процесс является аналогом поступательного перемещения фарша в шнековой мясорубке под воздействием давления стенок шнека, хотя с механической точки зрения сами по себе никакие точки шнека никуда поступательно не перемещаются, а просто осуществляют стационарное вращательное движение вокруг одного и того же центра, расположенного на оси шнека. Таким обр а зом, под воздействием псевдопотенциала U ( z , r , t ) в канале транспортировки возникает эффект "архимедова винта" (с чем, собственно, и связано название рассматриваемого эффекта "А-волна", или "архимедова волна", данное ему авторами).

Аналогом механических стенок архимедова винта выступают высокочастотные электрические поля, которые стационарно осциллируют с большой частотой на одном и том же месте пространства синхронно со стационарно осциллирующими электрическими напряжениями на электродах. Нельзя сказать, чтобы эти высокочастотные электрические поля куда-либо перемещались в пространстве, поскольку однонаправленная бегущая волна высокочастотного электрического поля

здесь очевидным образом отсутствует, а весь процесс ограничивается биениями на месте. Кроме того, после усреднения по времени высокочастотные электрические поля не приводят к появлению какого-либо эффективного ненулевого электрического поля, перемещающего заряженные частицы вдоль оси. Тем не менее совокупное воздействие высокочастотных электрических полей и инерционности движения заряженных частиц обеспечивает в конечном итоге равномерное поступательное перемещение заряженных частиц вдоль канала транспортировки в соответствии с эффектом архимедова винта.

Более подробно и аккуратно транспортировка ионов с помощью эффекта А-волны анализируется в [38–41].

Электрический потенциал высокочастотного электрического поля (21), к которому добавлены возмущающие пространственные гармоники (9), (10), описывается формулой

U ( z , r , t ) = U о x

X

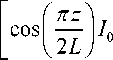
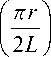
( 3nz J

^{+ £} cos I 2Ll ^e J I о

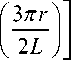
x

x cos Q t cos ( mt + ^ ) +

^{+ U} 0

■ I nz h sin I

1 2 L J ⁰

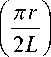
.     ■ I 3nz ] _T

+ s sm --- \L

I 2 L J ⁰

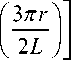
x

x sin Q t cos ( mt + ^ ) , ⁽²³⁾ где U ₀ — амплитуда колебаний электрического потенциала на оси системы, ε — относительный вклад третьей пространственной гармоники в электрическое поле на оси по сравнению с первой пространственной гармоникой, аддитивные фазовые смещения β и ψ , присутствующие в формуле (21), можно обнулить, если правильно выбрать начальные точки отсчета по координате z и по времени t , а остальные параметры в формуле (23) совпадают с аналогичными параметрами формулы (21).

Псевдопотенциал, который описывает усредненное движение заряженных частиц с массой m и зарядом e в высокочастотных электрических полях (21) в вакууме, имеет вид

U (z, r ) =

eπ ² U ₀² 16 mL ² ω ²

I 0 ²

+

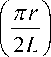
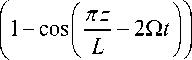
+ 1 1 ²

+

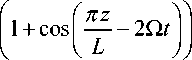
( 7Г |T 137Г V   (7ZI     127ZII

+ 6s Л — Л --- cos — — cos2

l 012L) 01 2L )l   l L )     l L

j I 7Г I ,

+ 1     Л

1 1 2 L ) 1

37Г V I 7Z ^ ( 27Z —— II cos| — | + cos| —

2 L

L

L

7 I — 201 II

)))

+

I

+ 9^ 2

l

3 πr

2 L

.         ( 3/7 Z| |

1 — cos     — 201 + l L))

3 πr

2 L

, I 3 7Z

1 + cos--2 0 1

l L

\

.

)_

a                                          b

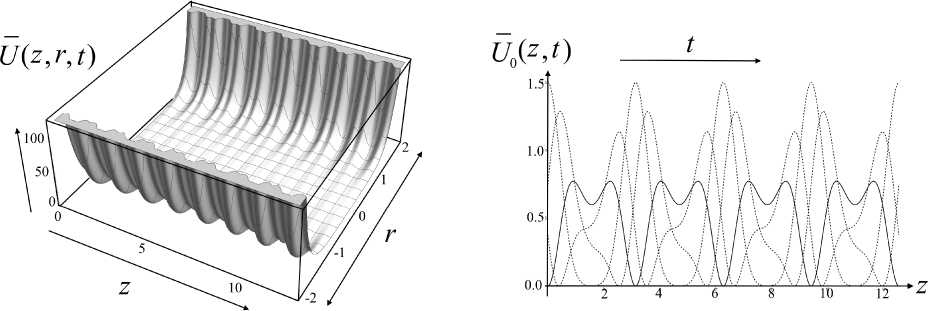
Рис. 10. Псевдопотенциал (24) в безразмерных нормированных координатах.

а — трехмерный график в плоскости ( z , r ) в некоторый момент времени, b — значение на оси r = 0 для двух разных моментов времени

График функции (24) в нормированных безразмерных координатах показан на рис. 10. Как и в предыдущих случаях, наличие дополнительных пространственных гармоник приводит к более резкому росту стенок псевдопотенциального желоба при приближении к краям круговых диафрагм, а также усложняет профиль гофрировки псевдопотенциала (рис. 10, а). Поскольку (24) описывает сразу несколько волн псевдопотенциала, распространяющихся вдоль оси с разными скоростями (включая стоячую волну, имеющую нулевую скорость), то процесс перестройки структуры локальных псевдопотенциальных ловушек выглядит достаточно сложно (рис. 10, b).

В частности, из-за интерференции волн в какие-то моменты времени волны псевдопотенциала суммируются, а высота стенок и наклон стенок локальных ловушек возрастают, а в какие-то моменты волны вычитаются, и высота барьеров во- круг локальных псевдопотенциальных ловушек резко уменьшается. Также возможно появление дополнительных локальных ловушек небольшой глубины в прежних точках максимума псевдопотенциала, которые, впрочем, быстро разрушаются (рис. 3, b). В результате в центральной области транспортирующего канала образуется сложная структура локальных псевдопотенциальных ловушек, в которых могут задерживаться заряженные частицы в процессе их изоляции и транспортировки.

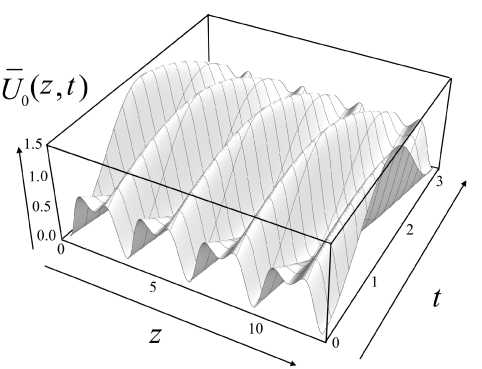
На рис. 11, а, показана эволюция профиля локальных ловушек в процессе транспортировки заряженных частиц в виде трехмерного графика изменения осевого распределения псевдопотенциала за один период смещения основной транспортирующей волны. На рис. 11, b, показаны "дорожки" минимумов осевого распределения псевдопотенциала, вдоль которых происходит транспортировка заряженных частиц (темные полосы на карте

a

b

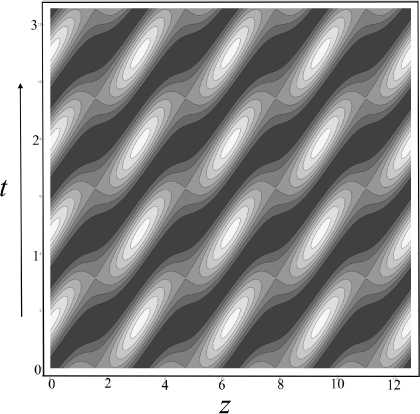
Рис. 11. Транспортировка заряженных частиц вдоль оси r = 0 с помощью бегущей волны псевдопотенциала (24) (эффект А-волны).

а — трехмерный график на плоскости ( z , t ) для транспортирующего псевдопотенциала U ( z , r, t ) = U 0 ( z , t ) , b — карта на плоскости ( z , t ) для эквипотенциальных линий транспортирующего псевдопотенциала и 0 ( _z , _t )

эквипотенциальных линий). Наглядно видно, что высота барьеров, ограничивающих локальные ловушки, становится то меньше, то больше, а область пространства, охватываемая ловушкой, становится то шире, то уже, хотя "дно" транспортирующих канавок, показанных на рис. 11, b, черным цветом, остается на нулевом уровне. Сам процесс движения сгустков заряженных частиц становится неравномерным, то ускоряясь, то замедляясь, хотя средняя скорость перемещения сгустков заряженных частиц остается прежней. Кроме того, из рис. 11, b, видно, что вдоль барьеров, разделяющих локальные псевдопотенциаль-ные ловушки, время от времени возникают локальные "перевалы", через которые заряженные частицы могут перепрыгивать между соседними локальными ловушками в определенные моменты времени. Все это делает процесс транспортировки заряженных частиц более сложным и запутанным, хотя сам эффект транспортировки заряженных частиц по принципу архимедовой волны псевдопотенциала в основном сохраняется.

В присутствии нейтрального газа псевдопотенциал (24) заменяется на демпфированный псевдопотенциал, отличающийся от выражения (24) наличием постоянного демпфирующего множителя ω2 / (ω2 + Ω2). Фаза синусоидальной амплитудной модуляции высокочастотных синусоидальных электрических напряжений, приложенных к электродам, разная на разных электродах, и, как следствие, фаза амплитудной модуляции высокочастотного электрического поля меняется в зависимости от рассматриваемой точки пространства. Однако, несмотря на такую специфическую модуляцию несущего высокочастотного синусоидального сигнала, фаза основных колебаний высокочастотного электрического поля (23) одинакова в любой точке пространства и совпадает с фазой высокочастотного сигнала cos(ωt + φ) в формуле (23). Поэтому псевдосила (3)–(5) равна нулю во всех точках пространства при наличии старших пространственных гармоник электрического поля точно так же, как и при отсутствии паразитных возмущений высокочастотного электрического поля (21).

За счет вязкого трения (6) ионы быстро теряют начальную кинетическую энергию, так что в конечном счете они оказываются на оси транспортирующего канала в локальных минимумах гофрировки псевдопотенциала. Однако теперь заряженные частицы могут накапливаться также в дополнительных локальных ловушках не слишком большой глубины, которые появляются на вершинах прежних максимумов осевого распределения псевдопотенциала (рис. 10 и рис. 11) по причине наличия старших пространственных гармоник высокочастотного электрического поля.

ЗАКЛЮЧЕНИЕ

В рамках псевдопотенциальной модели движения заряженных частиц в радиочастотных электрических полях было исследовано функционирование цилиндрических радиочастотных транспортирующих каналов. Были рассмотрены следующие режимы использования радиочастотных транспортирующих каналов:

• а)    высокочастотные синусоидальные напряжения со сдвигом фазы π между соседними круговыми диафрагмами;

• б)    высокочастотные синусоидальные напряжения со сдвигом фазы π / 2 между соседними круговыми диафрагмами;

• в)    амплитудно-модулированные высокочастотные синусоидальные напряжения, обеспечивающие транспортировку заряженных частиц в режиме А-волны.

В процессе проведения исследования использовались аналитические выражения для электрических полей радиочастотных цилиндрических транспортирующих каналов, полученные ранее в статье [1].

Авторы выражают свою искреннюю благодарность док-ру физ.-мат. наук Михаилу Игоревичу Явору, гл. научн. сотр. Института аналитического приборостроения РАН (г. Санкт-Петербург), за активное и деятельное участие в обсуждении рассматриваемой проблемы и указание на полезные литературные источники, использованные в данном исследовании.

Для аналитических вычислений и создания рисунков использовалась программа Wolfram Mathematica версии 11 Home Edition

.

Финансирование

Исследование выполнено в рамках Государственного задания Министерства науки и высшего образования Российской Федерации №  075-00444-25-00

(от 26.12.2024), тема НИР FFZM-2025-0006.