Моделирование деформаций земной поверхности в окрестности вулкана Суфриер Хиллз

Вулканизм — крупное планетарное явление, определяющее облик нашей планеты. В настоящее время ведется интенсивное наблюдение за активными вулканами. На них устанавливаются сейсмометры, датчики перемещений, постоянно действующие GPS-станции, осуществляются измерения деформаций поверхности при помощи наземного оборудования и радарной интерферометрии InSAR, производится мониторинг газового состава выбросов и их температуры, регистрируется интенсивность сейсмических сигналов. Из всего разнообразия способов оценки вулканической опасности измерение деформации земной поверхности является одним из самых чувствительных и надежных приемов слежения за глубинными магматическими явлениями [1, 2].

Наземные методы наблюдения в виде нивелировок и замеров расстояний недостаточно точно отражают реальные процессы деформирования территорий, требуют несоразмерных трудовых и материальных затрат. Исходя из этих данных невозможно строить какие-либо прогнозы вследствие малой частотности выполнения измерений [4]. Кроме того, при использовании высокоточных лазерных светодальномеров возникают сложности из-за рельефа местности и необходимости обеспечения оптической видимости [4].

В настоящее время интенсивно развиваются космические технологии, включающие Глобальную систему позиционирования (GPS) и радарную интерферометрию (InSAR) [3, 5, 6]. Однако в процессе наблюдения за вулканами в качестве основных недочетов исследователи отмечают неполное покрытие земной поверхности спутниками GPS и недостаточную частотность измерений [4–6]. Трудности при использовании InSAR-технологии связаны с наличием погрешностей, вносимых приземными слоями атмосферы и растительным или другим покровом исследуемой территории [4, 5].

В настоящее время одним из перспективных подходов к измерению физических величин, в частности деформаций, является применение волоконно-оптических датчиков. Волоконно-оптические средства регистрации обладают рядом преимуществ перед датчиками с другими принципами действия. Они отличаются высокой точностью измерения (до 10 ^{- 7} с учетом базы датчика [8]), не нуждаются в расположении источника электропитания в непосредственной близости и наличии электропроводящих (в том числе и информационных) сетей, инертны по отношению к агрессивной внешней среде [7]. Оптическое волокно, объединяющее все датчики, является одновременно проводником светового сигнала и информационным каналом. При помощи численных экспериментов была доказана возможность создания на основе волоконно-оптических технологий системы деформационного мониторинга земной поверхности в районах вулканической активности [9].

Необходимым элементом системы мониторинга является математическая модель деформационного поведения горных пород в окрестности вулкана. Благодаря моделированию напряженно-деформированного состояния горного массива, включающего вулканическую систему, появляется возможность оценить деформации земной поверхности вблизи источника возбуждения и подобрать инструментарий, необходимый для наблюдения поверхностного отклика на явления, происходящие в толще горных пород. Математическая модель позволяет проектировать состав элементов системы мониторинга и их конфигурацию, осуществлять интерпретацию экспериментальных данных, прогнозировать эволюцию деформационных процессов, проводить численные эксперименты, моделирующие возможные критические ситуации. Исходя из полученной информации устанавливаются основные параметры для построения собственно самой сети мониторинга.

В данной статье представлены результаты трехмерного моделирования деформационных процессов в горных породах в окрестности вулкана Суфриер Хиллз (о. Монтсеррат, Карибское море) с учетом особенностей строения очаговой и стволовой зон, неоднородности строения геологических пород горного массива и распределения магматического давления по глубине каналов и очагов вулкана. На базе построенной математической модели предложен вариант принципиального устройства системы мониторинга деформационного поведения вулкана.

2.    Моделирование напряженно-деформированного состояния горных пород в окрестности вулкана Суфриер Хиллз с учетом его внутреннего строения

Рассмотрим конструктивную схему вулкана Суфриер Хиллз. Она включает вулканическую постройку, систему каналов и магматических очагов, а также массив окружающих горных пород (Рис. 1). Территория, на которой находится вулкан, моделируется как пространственная область, и вследствие этого появляется возможность учитывать морфологические особенности как поверхностного слоя, так и внутренней структуры. Благодаря детальным геофизическим исследованиям установлено, что извержение магматических масс происходит через систему двух очагов [11]. Верхний очаг представляет собой вытянутый в вертикальном направлении эллипсоид вращения. Он связан с поверхностью земли узкой

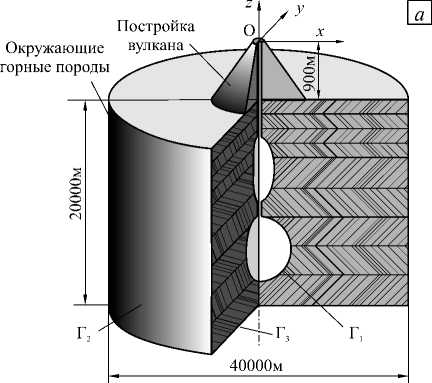
Рис. 1. Структурная схема горного массива в окрестности стволовой части вулкана ( а ) и форма очагов и каналов вулкана ( б )

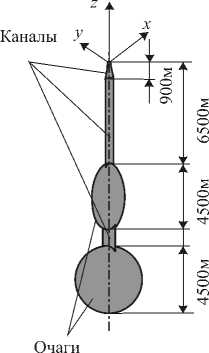
б

трещиной, переходящей по мере приближения к поверхности в канал эллиптического сечения. Нижний очаг, имеющий сферическую форму, соединен с верхним трещинообразным каналом и изолирован от нижележащей магматической системы. Плоскости верхней и нижней трещин взаимно перпендикулярны. Постройка вулкана представлена как усеченный конус, а прилегающая к ней территория — как плоскость. На рисунке 1 показаны характерные размеры основных частей вулканической системы. Радиус нижнего сферического очага равен 2246 м; верхний очаг — эллипсоид вращения, характеризуется полуосями 1131 м, 1131 м и 2262 м; каналы-трещины имеют сечения в виде эллипса с полуосями 0,1 х 750 м (нижняя) и 500 х 0,1 м (верхняя); сечение верхнего канала на уровне земной поверхности задается эллипсом с полуосями 14,9 х 32,2 м; высота вулканической постройки составляет 900 м.

Реальные породы, образующие остров Монтсеррат, обладают слоистым строением, поэтому геологическая структура горного массива представлена в модели в виде набора слоев толщиной 1000 и 2000 м, отличающихся физико-механическими характеристиками (модулем упругости, коэффициентом Пуассона). В таблице приведена информация о свойствах этих пород из [11, 12].

Таблица. Физико-механические характеристики материалов горных пород о. Монтсеррат

Глубина, км	Модуль упругости E , Па	Коэффициент Пуассона v	Глубина, км	Модуль упругости E , Па	Коэффициент Пуассона v
0–1	9,45·109	0,298	8–10	4,05·109	0,243
1–2	1,68·109	0,240	10–12	4,37·109	0,248
2–3	2,23·109	0,218	12–14	4,64·109	0,256
3–4	2,65·109	0,216	14–16	4,88·109	0,265
4–6	3,14·109	0,226	16–18	5,09·109	0,275
6–8	3,65·109	0,237	18–20	5,28·109	0,283

Для анализа состояния горных пород в окрестности вулкана необходимо совместно рассматривать процессы течения жидкой магмы в очагах и каналах вулканической системы и порождаемые ими изменения напряженно-деформированного состояния окружающих горных пород, испытывающих воздействие повышенного давления и температуры в очаге и каналах. Однако решение этой проблемы можно разделить на части: сначала проводить гидродинамический анализ неизотермического течения магмы в канале, а затем оценивать НДС окружающих горных пород. В настоящей работе не рассматривается течение жидкости в каналах и очагах. Воздействие жидкой магмы на массив горных пород учитывается путем приложения заданного давления, распределенного по поверхности каналов и очагов. Сведения о нем получены на основании расчетов, проведенных с использованием гидродинамических моделей течения магмы [10].

Для оценки напряженно-деформированного состояния горных пород берется фрагмент горного массива с вулканической постройкой, системой каналов и очагов и окружающей территорией (Рис. 1). Наличие горных пород, примыкающих к данной области, учитывается при помощи граничных условий: задается отсутствие перемещений (в вертикальном направлении — на нижней границе расчетной области, в горизонтальном направлении — на боковой поверхности) и нулевые сдвиговые напряжения на боковой и нижней границах. Остальные границы полагаются свободными. На основе численных экспериментов были установлены размеры выделенной области, обеспечивающие независимость результатов расчета от условий на удаленных границах — 20 км в глубину и столько же в радиальном направлении.

Деформационное поведение горных пород в окрестности вулкана моделируется в рамках линейной теории упругости. Это дает возможность выделить только те деформационные возмущения, которые вызываются изменением давления в очаговой зоне. При этом оценивается изменение деформированного состояния системы относительно «отсчетного», в качестве которого принято состояние вулканической системы, сформировавшееся под действием собственной тяжести горных пород.

Напряженно-деформированное состояние горных пород, возникающее от действия внутреннего давления, определяется из решения задачи с математической постановкой, включающей:

– уравнения равновесия

V-o = 0 ;

– физические уравнения и геометрические соотношения:

° = ХI '|Е)g + "' "=(1 . E -2v), Ц= 2(1^’ = = 2(Vu + (Vu)');

– граничные условия

– на поверхностях каналов и очагов ( Γ ₁ ):

σ n _{Γ 1} =- p ( t , z ) n ,

σ τ _{Γ 1} = 0;

– на нижней ( Γ ₂ ) и боковой ( Γ ₃ ) границах выделенной области:

z/ I = 0, zz I = 0, ст I = 0, ст I = 0; u_{z Γ2}     , u_{n Γ3}     ,      σ _{xz Γ2 ∪ Γ3}     ,      σ _{yz Γ2 ∪ Γ3}      ;

– на остальных поверхностях:

σ ⋅ n

Γ \( Γ ₁ ∪ Γ ₂ ∪ Γ ₃)

= 0.

Здесь: ∇ — оператор дивергенции; σ — тензор напряжений Коши; ε — тензор деформаций; g — единичный тензор; u — вектор перемещений; I ₁ ( ⋅ ) — первый инвариант тензора; λ , µ — коэффициенты Ляме; E — модуль упругости Юнга; ν — коэффициент Пуассона; n — вектор нормали к поверхности.

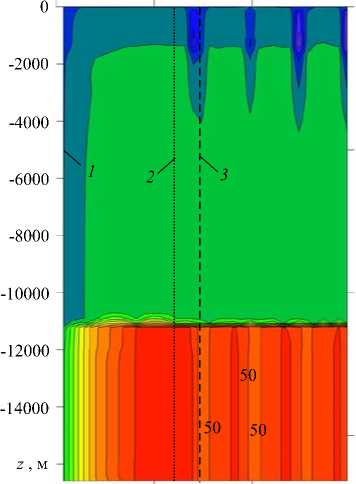
Давление на поверхности каналов и очагов вулканической системы ( Γ ₁ ) формируется как суперпозиция давления, вызванного весом вышележащих горных пород, и некоторого избыточного давления, возникающего вследствие происходящих в жидкой магме процессов. На рисунке 2 а представлено тоновое изображение распределения во времени и по глубине каналов избыточного давления. В нижнем очаге на протяжении достаточно компактного временного промежутка имеет место скачок давления. На глубине 11 км в зоне выхода из нижнего очага избыточное давление поднимается от 0 до ~ 45 МПа. В то же время в приповерхностной зоне на глубине до 2 км наблюдается сначала увеличение магматического давления (избыточное давление ~ + 5 МПа), а затем резкий спад (до - 20 МПа). Подобные изменения давления происходят с определенной периодичностью во времени, тогда как давление в нижнем очаге остается на прежнем уровне. На рисунке 2 б показано распределение давления в системе каналов и очагов, отвечающее трем моментам времени: 1-й момент — невозмущенное состояние (линия 1 ); 2-й момент — через 2700 час (112,5 суток) от начала вулканического процесса, что соответствует повышенному давлению во всей магматической системе вулкана (линия 2 ); 3-й момент — через 2820 час (117,5 суток) от начала при повышенном давлении в обоих очагах и пониженном давлении в приповерхностной области (линия 3 ). Давление в стволе вулкана изменяется с течением времени, однако эти изменения достаточно медленны, поэтому можно принять допущение, что окружающие горные породы находится в квазистатическом состоянии.

а

2000        4000 t, час

-5

-10

-15

-20

-25

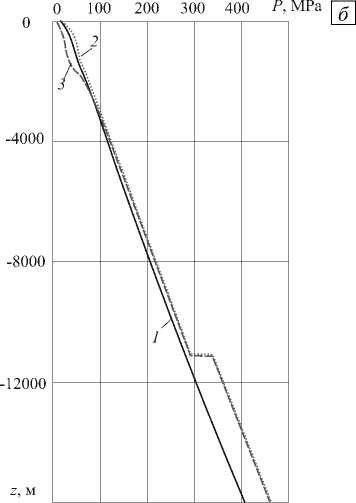
Рис. 2. Эволюция избыточного давления магмы ( а ) и распределение давления по глубине ствола вулкана ( б ) в момент времени t = 0 (кривая 1 ), через 2700 ( 2 ) и 2820 ( 3 ) час

3.    Результаты численного моделирования деформации земной поверхностив окрестности вулкана Суфриер Хиллз

Численное моделирование напряженно-деформированного состояния горных пород в окрестности магматического очага осуществляется методом конечных элементов с использованием программного комплекса ANSYS. При этом, исходя из изменения давления в очаге и каналах вулканической системы, выделяется три основных режима функционирования вулканической системы: отсчетный, при котором вулканическая активность отсутствует, и два режима, отвечающих возбужденному состоянию вулканической системы (первый из них характеризуется повышенным избыточным давлением в глубинной области (на глубине более 11 км в зоне нижнего очага), второй — пониженным избыточным давлением в вышележащих слоях (верхний очаг и поверхности двух взаимно перпендикулярных трещин)). Согласно указанным режимам можно рассматривать три деформационных состояния окружающих пород: отсчетное — сформировавшееся от воздействия веса горных пород, и два измененных. Описание деформационного поведения горного массива в рамках линейной теории упругости позволяет представить деформацию земной поверхности в виде суперпозиции деформаций, вызванных данными активными процессами. Сопоставление деформационных полей в отсчетном и измененных состояниях системы обнаруживает деформационный отклик на изменения давления стволовой части вулкана и дает понять, возможна ли регистрация изменений деформаций земной поверхности с помощью известных средств их измерения.

В силу геометрии расчетной области (см. Рис. 1) можно выделить плоскости симметрии, совпадающие с координатными плоскостями O zx и O zy . Полученные результаты представляются далее с учетом этой симметрии. Ниже приведены распределения избыточных радиальных и окружных деформаций по поверхности вулканической постройки и прилегающей к ней области, а также по траекториям, проходящим по склону вулкана и окрестной территории в направлении осей O x и O y .

• 3.1.    Деформационный отклик земной поверхности в окрестности вулкана Суфриер Хиллз на магматические процессы в глубинной зоне

• 3.2.    Деформационный отклик земной поверхности в окрестности вулкана Суфриер Хиллз на магматические процессы в приповерхностной зоне

  Возмущение деформационного поля, провоцируемое процессами в верхнем очаге и обоих каналах, отвечающее моменту времени 2820 час (117,5 суток), моделируется следующими граничными условиями: на глубине более 11 км избыточное давление полагается нулевым, а в вышележащей зоне — изменяющимся от 0 до - 20МПа в соответствии с кривой 3 на рисунке 2 б . На рисунке 4 изображены дополнительные деформации земной поверхности, возникающие в ответ на эти процессы. Деформационные поля имеют существенно несимметричный характер: изолинии как радиальных, так и окружных деформаций вытянуты в направлении оси y . Несимметричность деформационного поля наиболее заметна в области проекции трещины, а на расстоянии ~ 8 км от оси вулкана она практически нивелируется. Рисунок 5 демонстрирует распределение окружных и радиальных деформаций в зависимости от радиальной координаты. Из рисунка видно, что окружные деформации значительно превосходят радиальные: так, в точке, удаленной на 4 км от оси симметрии в направлении О x , величина Б _ф составляет ~ 7 - 10 - 5 , а б r --3 ■ 10 ^{- 6}. То же самое можно сказать и в отношении дистанции, на протяжении которой деформационный след остается значимым: ε _r достигает значения 10 ^{- 6} приблизительно в 7 км от центра, а ε _r — на расстоянии порядка 16 км.

Магматические процессы, происходящие в глубинной части вулканической системы, моделируются граничным условием для давления, приложенного к стенкам очагов и трещин:

_ f0,    z >-11 км, p {46,5 МПа, z <-11 км.

Возмущение деформационного поля земной поверхности, соответствующее приложенному давлению, изображено на рисунке 3. Проведенные расчеты показывают, что распределение радиальных ( б r ) и окружных ( в_ф ) деформаций имеет характер, близкий к осесимметричному. Несмотря на наличие трещинных каналов, изменения давления в глубинной зоне вызывают на поверхности земли деформации, характер распределения которых не демонстрирует чувствительности к форме трещин. Анализ полученных данных позволяет выделить область, в пределах которой возможна регистрация возмущения деформационного поля на поверхности земли с помощью существующих средств измерения.

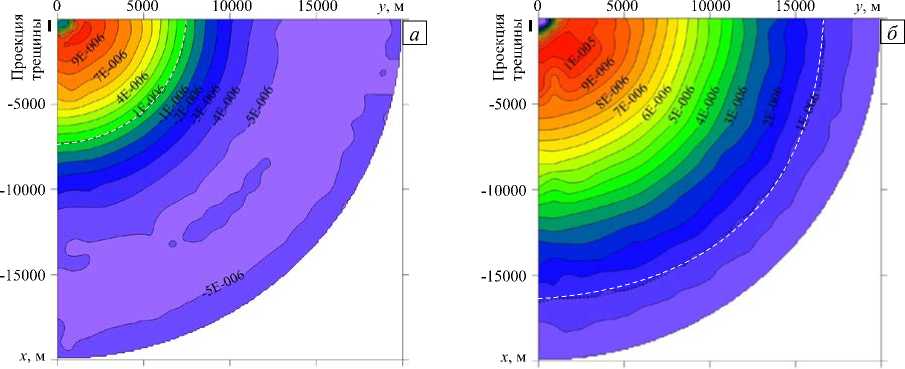
Рис. 3 Распределения дополнительных деформаций земной поверхности - радиальных s _f ( а ) и окружных s_p ( б ), вызванных подъемом давления в глубинной части вулканической системы

Используемые в настоящее время волоконно-оптические датчики на основе брэгговских решеток обеспечивают точность измерения ~ 10 - 7 [8]. Надежная регистрация деформаций с помощью мониторинговой системы, базирующейся на датчиках такого типа, может осуществляться в пределах области, где деформации на порядок превосходят точность измерения, то есть их значения не ниже 10 ^{- 6} . Эта зона лежит в пределах окружности радиуса ~ 7 км для радиальных деформаций и ~ 17 км для окружных деформаций (на рисунке выделена штриховой линией).

Сопоставление деформационных полей на рисунках 3 и 4, позволяет сделать вывод, что деформационные следы от глубинных и приповерхностных процессов отличаются не только по форме, но и по величине. Рисунок 6 демонстрирует изменение радиальных ( ε _r ) и окружных ( ε _ϕ ) деформаций на поверхности по мере удаления от центральной оси вулкана вдоль направления O x (совпадающего с ориентацией верхней трещины). На дистанции до 8 км окружные деформации от приповерхностных процессов существенно превосходят деформации, порождаемые глубинными процессами. Различие в величине радиальных деформаций в пределах указанной области на порядок меньше.

Анализ установленной с помощью численных экспериментов картины напряженно-деформированного состояния поверхности земли в окрестности действующего вулкана Суфриер Хиллз показывает, что возмущения деформационного поля, вызванные происходящими в системе очагов и каналов вулкана магматическими процессами, в окрестности до 4 км от центра вулкана имеют величину

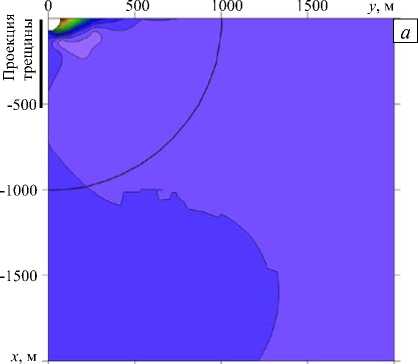
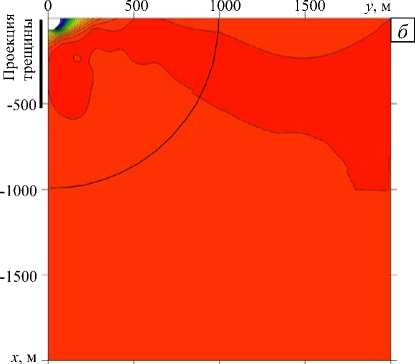
Рис. 4. Распределения дополнительных деформаций земной поверхности – радиальных ε _r ( а ) и окружных ε_ϕ ( б ), отвечающих пониженному давлению в верхней части вулканической системы

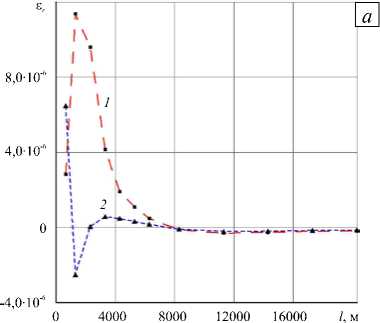
Рис. 5. Распределение по траекториям x = 0 (кривая 1 ) и y = 0 ( 2 ) радиальных – ε _r ( а ), и окружных – ε_ϕ ( б ), деформаций земной поверхности, вызванных приповерхностными процессами

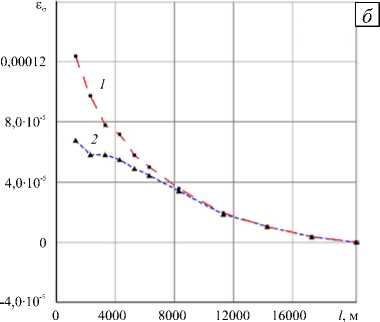
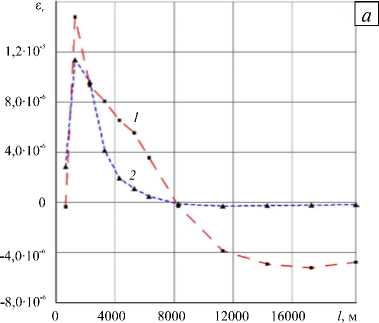
Рис. 6. Распределение вдоль траектории x = 0 радиальных – ε _r ( а ) и окружных – ε_ϕ ( б ) деформаций земной поверхности, вызванных глубинными процессами (кривая 1 ) и приповерхностными процессами ( 2 )

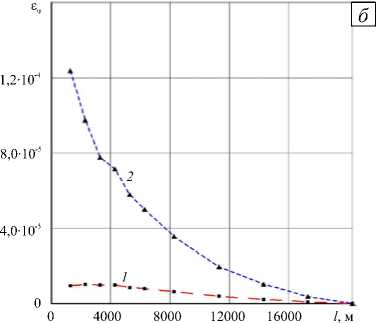
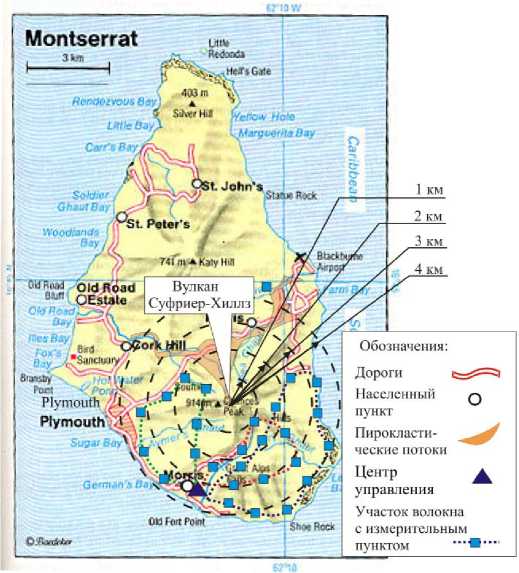
Рис. 7. Структурная схема автоматизированной системы деформационного мониторинга окрестности вулкана на основе волоконно-оптических датчиков с брэгговскими решетками»

порядка 10 ^{- 5} - 10 ^{- 6}. Такие возмущения могут быть зафиксированы датчиками деформации на основе волоконно-оптических элементов. Результаты моделирования изменений деформационного поля в толще и на поверхности горного массива под воздействием определенным образом заданных процессов внутри системы очагов и каналов позволяют подойти и к обратной задаче — к оценке явлений в вулканической системе на основании регистрируемых изменений деформационного поля на поверхности.

Рассмотренный подход позволяет предложить следующую принципиальную схему системы мониторинга деформаций земной поверхности в окрестности вулкана Суфриер-Хиллз. (Рис. 7). В качестве главной составляющей системы мониторинга могут быть использованы волоконно-оптические датчики на базе брэгговских решеток. Сеть датчиков рационально организовать в виде трех замкнутых линейных участков волокна, которые должны быть расположены на поверхности земли у подножья постройки вулкана. Из соображений безопасности мониторинговой системы предлагается разместить сеть датчиков только в южной части вулканической территории, свободной от распространения пирокластических потоков, при этом использовать местность вдоль имеющихся дорог и участка береговой линии. Это обстоятельство не снизит информативности системы в силу симметричности картины ожидаемого деформационного отклика. Предлагаемая схема размещения волокна обеспечит регистрацию деформаций земной поверхности на удалении от 1 до 4 км от центральной оси вулкана в режиме реального времени. Согласно полученным данным моделирования деформационного отклика на приповерхностные вулканические процессы в этой зоне его ожидаемая величина колеблется от -3 ⋅10-6 до +9⋅10-6 для радиальных деформаций и от 5⋅ 10-5 до 12 ⋅ 10-5 для окружных деформаций. Ожидаемый отклик на глубинные процессы составляет, соответственно, порядка 10-6 для радиальных и 10-5 для окружных деформаций.

На каждом линейном участке системы предполагается разместить по 8–12 измерительных пунктов, отдаленных на 500–700 м друг от друга. В каждом измерительном пункте должно содержаться по три датчика на основе брэгговских решеток: два датчика ориентированы таким образом, чтобы могли регистрировать деформации в двух взаимно перпендикулярных направлениях в плоскости, нормальной к вектору силы тяжести; третий датчик необходим для компенсации температурного влияния. Начало и конец каждого оптического линейного участка волокна замыкаются на центр управления мониторинговой системы (Рис. 7), в котором располагается специализированное лазерное устройство — интеррогатор, генерирующее необходимый волновой пакет светового импульса. По искажению свойств (частоты сигнала) этого пакета, прошедшего весь путь по соответствующей волоконной линии, можно однозначно судить об уровне деформации, фиксируемом каждым датчиком этой линии. Работа интеррогатора управляется компьютером, который задает уровень частотности опроса датчиков, оценивает состояние их работоспособности. Этот же компьютер осуществляет сбор информации с интеррогатора, то есть данные измерения деформации всеми датчиками. Далее эта информация подвергается математической обработке и дальнейшему анализу, в значительной степени опирающемуся на разработанную математическую модель деформационного состояния горного массива. Центр управления всей системой может быть расположен на территории одного из населенных пунктов вблизи вулкана.

Система мониторинга подобной структуры позволит в режиме реального времени надежно регистрировать изменения полей деформации, вызванные вулканическими процессами в зонах как верхнего, так и нижнего очагов. Кроме того, она дает возможность по величине отклика и его форме (симметричной или согласующейся с конфигурацией трещин) идентифицировать, в какой части системы вулканических каналов и трещин происходят процессы, откликами которых являются регистрируемые изменения деформационного поля.

4.    Заключение

Проанализировано напряженно-деформированное состояние горных пород с учетом неоднородности их свойств в окрестности вулкана, имеющего два очага извержения, соединенные трещинными каналами. Получены распределения деформаций земной поверхности на склонах вулканической постройки и на прилегающей территории.

Показано, что отклик земной поверхности на изменения давления магмы в глубинной области вулканической системы регистрируется как осесимметричный (при заданной точности измерения деформаций). Наиболее существенные деформации земной поверхности вызываются изменениями давления магмы в верхней зоне вулканической системы, и наиболее чувствительны к ним окружные деформации ε_ϕ .

Разработанная математическая модель определения НДС отражает особенности квазистатических деформационных процессов в горных породах, окружающих вулкан. Эта модель, являясь неотъемлемой частью системы деформационного мониторинга, во взаимодействии с математической моделью, описывающей гидродинамику магмы, позволяет интерпретировать показания датчиков системы мониторинга, а анализ результатов интерпретации — прогнозировать время наступления активной фазы вулканической деятельности.

Предложена принципиальная структурная схема системы мониторинга состояния вулкана Суфриер Хиллз, измерительными элементами которой являются волоконно-оптические датчики на основе брэгговских решеток. Система мониторинга способна в режиме реального времени регистрировать изменения деформационного поля на территории вулкана от действия вулканических процессов.

Подобные системы деформационного мониторинга могут быть использованы для наблюдения за состоянием и других вулканов, деятельность которых сопровождается ростом лавовых куполов. К таким вулканам относятся Безымянный в России (на Камчатке), Сантьягито в Гватемале, Майон в Индонезии.

Работа выполнена при финансовой поддержке РФФИ (проекты № 12-08-01000-а, № 13-08-96069).