Моделирование деформирования и разрушения фибриллярных структур

Перспективным сырьем для создания новых биологически совместимых материалов являются аномальные (амилоидные) фибриллы. Бурное развитие экспериментальных методов, таких как, например, атомно-силовая микроскопия, позволило подробно изучить механические свойства отдельной фибриллы [1–3]. В работе [1] описаны механические свойства единичных амилоидных фибрилл, полученные методами атомно-силовой микроскопии и спектроскопии. Показано, что эти самообразованные из белка инсулина материалы имеют прочность 0,6±0,4 ГПа,

сравнимую с прочностью стали (0,6–1,8 ГПа), и модуль Юнга 3,3±0,4 ГПа, сравнимый с модулем шелка (1–10 ГПа). Здесь под прочностью фибрилл понимается значение максимальных растягивающих напряжений, при которых происходит их разрыв. В работе [2] установлена связь аномальных механических свойств амилоидных фибрилл с их внутренней структурой. Приведенные данные показывают, что фибриллы являются крайне привлекательными с точки зрения технологического использования. Теоретическая модель эксперимента по определению механических свойств фибриллы предложена в [3]. Несмотря на интенсивность работ в данной области, окончательного понимания особенностей механического поведения амилоидных фибрилл пока достигнуть не удалось. Об этом свидетельствуют расхождения между результатами различных работ, отмеченные в [3].

В настоящее время ведутся работы по созданию материала на основе фибрилл. Подобный материал представляет собой ткань, имеющую случайную структуру и состоящую из фибрилл, скрепленных между собой за счет химически активных ферментов. Однако исследования в этом направлении далеки от завершения [4].

Самостоятельный научный интерес представляет построение моделей такого рода материалов. При этом возникает проблема определения механических свойств материалов со случайной структурой. Особое внимание в литературе уделяется моделям сетей, образованных различными биологическими элементами (чаще всего полимерными нитями). Простейшие модели, позволяющие аналитически описать свойства полимерных материалов, предложены в [5–8]. В этих работах элементарный объем материала (резины) представляется в виде совокупности полимерных нитей, расположенных определенным образом. Такой подход позволяет описать поведение материала при больших деформациях. Позднее аналитические модели использованы, в частности, для имитации биологических тканей человека, в состав которых входят колагеновые фибриллы [9–11]. Однако данные модели не учитывают изгибную жесткость фибрилл и не позволяют описать процесс разрушения материала. В работах [12, 13] рассматривается задача определения упругих свойств биоматериала в двухмерной постановке. На плоскость случайным образом добавляются упругие стержни различной длины. Считается, что в точках пересечения стержни скреплены абсолютно жестко. В аналитическом подходе вводится предположение об аффинности деформаций (то есть все стержни деформируются как соответствующие отрезки воображаемой сплошной среды) и вычисляется модуль сдвига системы. При компьютерном моделировании минимизируется энергия всей системы, которая складывается только из энергии растяжения и изгиба каждого стержня по первой форме. Сравнение результатов двух подходов показывает, что предположение об аффинности является слишком грубым приближением и может привести к значительным ошибкам.

Описание процессов сильного деформирования и разрушения с помощью вышеперечисленных моделей представляется весьма сложной задачей. В такой ситуации незаменимую роль играет метод молекулярной динамики [14, 15] или его обобщение — метод частиц [16]. В литературе оба метода используются, как правило, только для описания процессов формирования фибрилл [17].

В данной работе предлагается двухмерная молекулярно-динамическая модель материала на основе фибрилл. Одиночная фибрилла представляется двухслойной полосой, состоящей из частиц, взаимодействие которых определяется потенциалом Леннарда–Джонса. Для получения материала фибриллы добавляются на плоскость случайным образом и скрепляются в местах пересечения. Далее, строится диаграмма деформирования такого материала и исследуется влияние начального распределения и числа фибрилл в образце на его механические характеристики. Кроме того, вводится параметр, отвечающий за упорядоченность фибрилл в одном из направлений, и строится зависимость модуля Юнга материала от этого параметра.

2.    Построение модели материала на основе фибрилл

В качестве простейшей модели, способной описать процессы деформирования и разрушения материала, берется одиночная фибрилла — полоса из двух слоев частиц, расположенных в узлах треугольной решетки (Рис. 1). Длина фибриллы полагается равной 50 a ₀ , где a ₀ — равновесное расстояние между частицами. Механические свойства двухслойной полосы достаточно хорошо изучены теоретически. Связь параметров потенциала взаимодействия с упругими модулями полосы определена, например, в работах [18, 19].

Прежде чем перейти к компьютерной модели, следует кратко описать экспериментальный подход к созданию материала на основе фибрилл. Изначально фибриллы выращиваются в растворе [4]. Затем туда добавляется специальный активный фермент, обеспечивающий сшивание фибрилл в местах пересечения. Через некоторое время растворитель испаряется и остается чистый материал, моделированию которого и посвящается данная работа.

При построении модели материала используется следующая процедура. С помощью генератора случайных чисел задаются координаты центров масс фибрилл в диапазоне x , y ∈ (0; 100 a ₀). Ориентация фибрилл на плоскости характеризуется

Рис. 1. Модель одиночной фибриллы.

Рис. 2. Образцы различной плотности (50, 100, 150, 200 фибрилл)

углом ф , равномерно распределенным в интервале [0; 2 п ]. На рисунке 2 приведены образцы с различными значениями плотности (числом фибрилл, приходящихся на единицу площади). Видно, что вне зависимости от плотности все они сильно неоднородны. Ниже будет показано, что это ведет к значительному разбросу в значениях упругих модулей.

Исследование эффектов, связанных с тепловым движением частиц (температурой) выходит за рамки данной работы. Поэтому в начальный момент времени скорости частиц задаются равными нулю. Тепловое движение, появляющееся в результате деформирования образца, практически полностью гасится за счет специальной процедуры деформирования, о которой речь пойдет далее. В частности, для устранения эффектов, связанных с тепловым движением, вводятся силы вязкого трения.

Важную роль при построении модели материала играет закон взаимодействия между фибриллами. Как уже упоминалось, скрепление фибрилл предполагается проводить за счет химической реакции фибрилл с ферментом. В силу малости зоны сцепления в сравнении с длиной фибриллы ее податливость не учитывается. Поэтому принимается решение моделировать сцепление пружинками большой жесткости (много большей жесткости связи).

• 3.    Основные результаты

  • 3.1.    Диаграмма деформирования

Для построения диаграммы деформирования исследуемого материала проведен следующий эксперимент. Рассматривался квадратный образец x , y е (0;100 а ₀), содержащий 150 фибрилл, при следующих граничных условиях:

ux = 0, 0 < x < A, ls - А < x < ls,uy = 0, 0 < y < A, ls - A < y < ls,

где u x , u_y — компоненты векторов перемещений частиц; l_s = 100 а ₀ — длина образца; А — размер области приложения граничных условий. В экспериментах взято А = 15 а ₀. Иными словами, у всех частиц, лежащих от границ на расстояниях, меньших А , фиксировалась одна из координат вектора перемещения, что позволяло добиться одноосной деформации образца. Далее проводилось аффинное деформирование вдоль оси y , для чего через промежутки времени, равные 4 T ₀ , задавалась аффинная деформация 0,005% (все точки системы смещались в новые положения, соответствующие однородной макроскопической деформации образца). Здесь T ₀ — характерный временной масштаб модели, равный периоду малых колебаний частицы на пружинке с жесткостью, равной жесткости связи. Кроме того, в систему вводилось вязкое трение с коэффициентом трения b = 0,03 B ₀, где B ₀ — критическое значение коэффициента вязкого трения (значение, при котором движение частицы в поле Леннарда–Джонса вблизи положения равновесия перестает быть колебательным). Такой способ деформирования выбран в связи с тем, что он позволяет избежать нежелательных волновых процессов в образце.

Диаграмма деформирования приведена на рисунке 3. Следует отметить, что при моделировании разрушения никаких дополнительных критериев не вводилось. Разрушение образца наступало при разрыве связей между частицами, описываемых потенциалом Леннарда–Джонса.

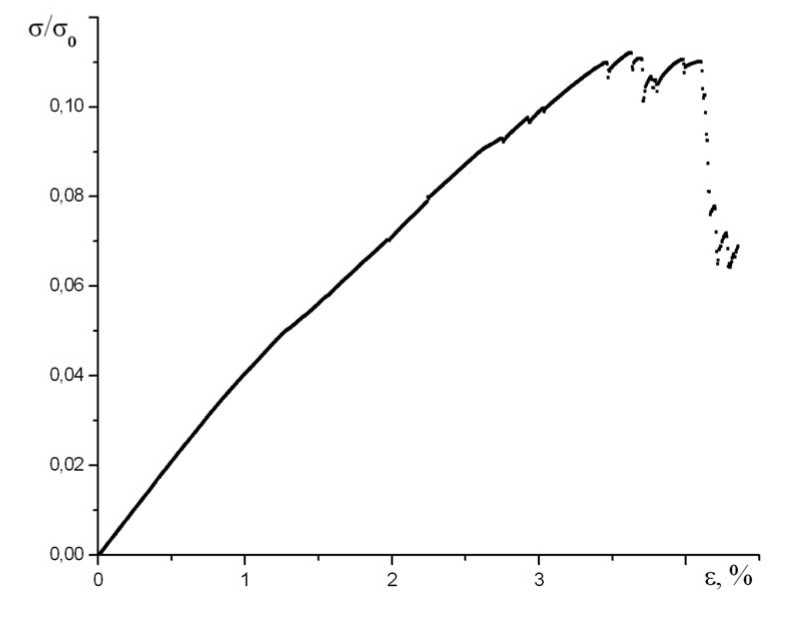
Рис. 3. Диаграмма деформирования компьютерного материала на основе фибрилл ( σ ₀ = f _*/ a ₀ ² ; f _* - максимальная сила, соответствующая потенциалу Леннарда-Джонса)

Нетрудно видеть, что разрушение наступало при деформации 3–4%, в то время как одиночная фибрилла разрушается при деформации примерно 10%. Причиной более раннего разрушения образца является сильная неоднородность материала, вызванная отсутствием механизмов упорядочивания фибрилл. Неоднородность пространственного распределения фибрилл приводит к неравномерному распределению энергии деформации между фибриллами, которое, в свою очередь, приводит к разрушению. Таким образом, есть основания полагать, что упорядочивание фибрилл приведет к значительному увеличению прочностных характеристик материала.

• 3.2.    Влияние начального распределения и плотности материала на упругие свойства

Случайность начальной конфигурации может повлиять не только на прочностные характеристики, но и на экспериментально определяемые значения упругих модулей. Для проверки данного утверждения проведена серия из 50 экспериментов. Результаты для образца, содержащего 100 фибрилл, представлены на рисунке 4. Модуль Юнга материала вычислялся как отношение суммарной силы, действующей на границе образца в условиях одноосной деформации, к площади границы, умноженной на значение деформации (при вычислении площади считалось, что толщина образца равна a ₀ ).

Из графика видно, что различие в начальных конфигурациях может привести к отличиям в модуле Юнга почти в два раза. Однако точность вычисления модуля упругости в компьютерном эксперименте определялась среднеквадратическим отклонением δ . В данном случае δ составляло около 20%. Анализ экспериментальных данных, приведенных в работе [1], показал, что модуль Юнга одной фибриллы определялся с точностью порядка 10%, следовательно, точности, получаемой в компьютерном эксперименте, вполне достаточно для практических целей.

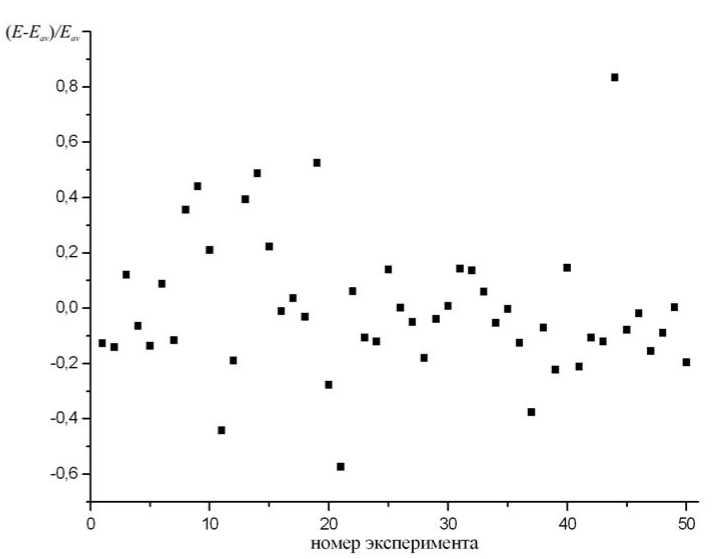
Рис. 4. Зависимость модуля Юнга E образца от начального распределения фибрилл ( E _av — средний модуль Юнга)

При исследовании зависимости модуля Юнга от плотности фибрилл фиксировался размер образца (как и ранее x,у е (0; 100 a 0 )) и увеличивалось число фибрилл в интервале от 100 до 200. Для устранения разброса, вызванного случайностью начальной конфигурации, для каждого числа фибрилл проводилась серия из 50 экспериментов. График искомой зависимости, полученный в результате моделирования, приведен на рисунке 5.

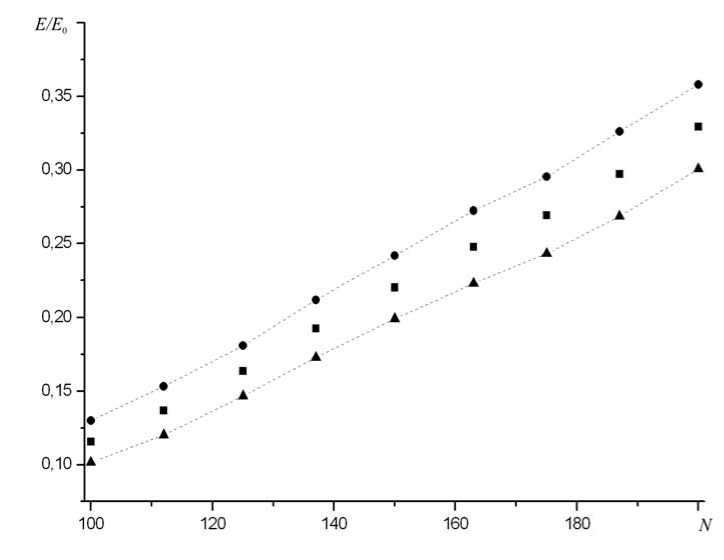
Рис. 5. Зависимость модуля Юнга образца E от числа фибрилл N , E ₀ – модуль Юнга бесконечного монокристалла. Пунктирными линиями соединены точки ( E/E 0 ) ( 1 ± 0,5 5 ) , соответствующие границам доверительного интервала

Из рисунка видно, что модуль Юнга материала растет практически линейно с ростом числа фибрилл. Среднеквадратическое отклонение модуля Юнга падает с ростом числа фибрилл с 25% (для 100 фибрилл) до 17% (для 200 фибрилл).

• 3.3.    Влияние упорядоченности фибрилл на упругие свойства материала

Для оценки влияния упорядоченности фибрилл на механические свойства материала использовалась следующая процедура. С помощью генератора случайных чисел задавались положение центра масс фибриллы в диапазоне x , у е (0;100 а ₀) и ее ориентация. Ориентация определялась с помощью вектора, исходящего из начала координат и равномерно распределенного в эллипсе, заданном уравнением ( kx ) 2 + у ² = 1. Коэффициент к <  1 характеризовал степень упорядоченности фибрилл вдоль оси у . При к = 1 направления вдоль обеих осей равновероятны, следовательно, свойства не зависят от направления приложения нагрузки. Начальные конфигурации, полученные при нескольких значениях параметра k , приведены на рисунке 6.

Влияние параметра k на модули упругости материала оценивалось из следующего компьютерного эксперимента. Определялся модуль Юнга вдоль оси y для образца, содержащего 150 фибрилл длиной 50 a ₀ . При этом параметр k менялся в промежутке [0; 1]. Для уменьшения разброса экспериментальных данных, вызванного случайностью начальной геометрии, для каждого значения k проводилась серия из 10 экспериментов. Получившаяся зависимость модуля Юнга от параметра k приведена на рисунке 7. При этом значение E max вычислялось по формуле E max = (l_f/l_s ) ( NC1 /S ) , где S — площадь сечения образца (при вычислении площади считалось, что толщина образца равна a ₀ ), N — число фибрилл, C ₁ — жесткость одиночной фибриллы на растяжение, имеющая размерность силы (жесткость на растяжение эквивалентного стержня [18]), l_s , l_f — длины образца и одиночной фибриллы соответственно (в данном эксперименте l f = 50 а 0 , l_s = 100 а ₀). E max соответствует гипотетическому материалу, получаемому следующим образом. Из всех имеющихся фибрилл создаются нити длинной l_s , которые располагаются параллельно направлению деформирования.

Из графика видно, что при стремлении k к единице модуль Юнга материала убывает практически линейно. Отметим, что при уменьшении k модуль Юнга не стремится к значению E _max . Объясняется это тем, что даже при полном упорядочивании ( к = 0) фибриллы, как правило, не образуют нити длиной l s , направленные вдоль оси у . Например, вполне вероятной является конфигурация, при которой фибриллы располагаются, не пересекаясь. Очевидно, в таком случае модуль Юнга материала

Рис. 6. Начальные конфигурации, при различных значениях параметра к (слева направо: к = 0,1; 0,5; 1,0)

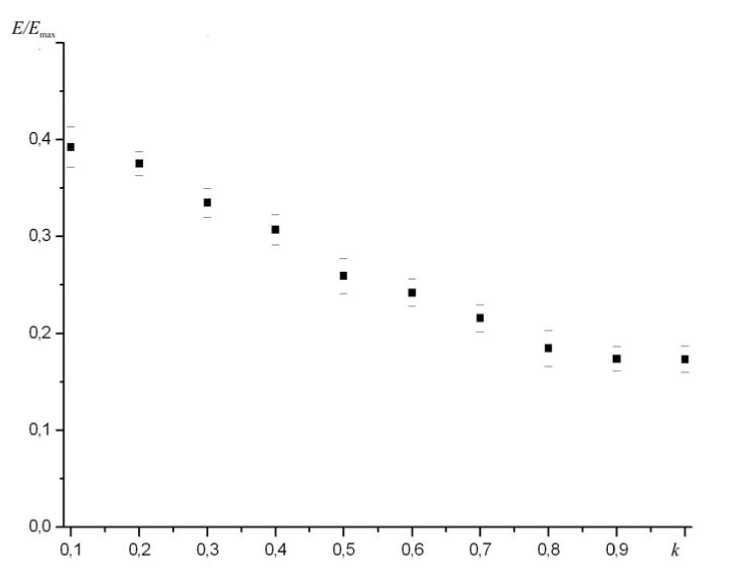
Рис. 7. Зависимость модуля Юнга вдоль оси y от параметра k равняется нулю. Следовательно, при полном упорядочивании фибрилл модуль Юнга материала может принимать любое значение в интервале (0; Emax).

Кроме того, из рисунка 7 видно, что упорядочивание фибрилл может увеличить модуль Юнга материала в данном направлении примерно в 2 раза. Однако следует отметить, что при этом в ортогональном направлении модуль Юнга уменьшается. Следовательно, для создания изотропного материала необходимо либо накладывать листы из фибрилл друг на друга, либо разрабатывать процедуру, позволяющую проводить упорядочивание одновременно в двух направлениях.

4.    Заключение

В работе предложены простейшая двухмерная модель одиночной фибриллы и процедура создания материала на основе фибрилл. Для модельного материала построена диаграмма деформирования. Показано, что разрушение образца происходит при деформации ~ 3%, в то время как принятая модель одиночной фибриллы разрушается при деформации ~ 10%. Исследованы зависимости модуля Юнга от случайного начального распределения фибрилл в образце и плотности образца. Показано, что модуль Юнга отдельных образцов может почти в 2 раза отличаться от среднего значения. При этом среднеквадратическое отклонение составляет порядка 20% и убывает с ростом плотности образца. Модуль Юнга линейно растет с ростом плотности. Введен параметр, характеризующий упорядоченность фибрилл в одном направлении. Показано, что модуль Юнга материала в данном направлении увеличивается до 2,5 раз.

Авторы благодарны О.И. Киселеву, В.В. Егорову, А.В. Черкаеву за полезные обсуждения.

Работа выполнена при финансовой поддержке государственного контракта № 02.513.11.3231 и Российского фонда фундаментальных исследований (проект № 08-01-00865-a).