Моделирование диффузорных течений жидкости посредством редуцированных уравнений

• 1.    Постановка задачи и комментарии к предмету исследования

Необходимость отыскания точных и приближенных (в том или ином смысле) аналитических выражений для решений модельных уравнений гидродинамики возникает при изучении и создании многих технических устройств. Например, описание динамических характеристик жидкости в гидроциклонах и диффузорах имеет большое значение для задачи оптимизации технических характеристик проточных частей турбинных насосов, участвующих в перекачке нефти по магистральным трубопроводам. Описание же динамических характеристик жидкости в этих устройствах можно получить на. основе имеющихся аналитических выражений для решений модельных уравнений гидродинамики, используемых в подобных задачах, или их упрощенных вариантов.

Упрощенные варианты уравнения Навье - Стокса, используются при изучении диффузорных течений, начиная с основополагающих работ Джеффри [1] и Гамеля [2] (1915 и 1917 гг.). Сведения по математическому моделированию на. этой основе течений в плоском диффузоре можно найти в [3-6].

Цель статьи 1 заключена, в демонстрации того, что задача, о динамике жидкости в диффузорах (плоском, объемном и диффузоре-улитке) допускает применение нелокальной ре-

• ¹    Работа выполнена при поддержке ОАО «Турбонасос».

2.    Двумерные уравнения Навье – Стокса и Гельмгольца

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ дуцирующей схемы Ляпунова – Шмидта, посредством которой можно сколь угодно точно описывать поле скоростей частиц жидкости в областях произвольных геометрических форм. При таком подходе извлекается и дополнительная информация о «качественных свойствах» течений, полученная на основе аналитических и геометрических свойств так называемых ключевых отображений и ключевых функций [7].

Часто базой вычислительного процесса в случае плоского диффузора является функциональная редукция к краевой задаче для ОДУ (посредством подстановки Гамеля для вихревой функции) с последующим использованием свойства полной интегрируемости полученного ОДУ. Но, как известно, представление решений через эллиптические функции не удовлетворяет современным требованиям к точности приближений — вследствие недостаточной точности существующих таблиц значений эллиптических функций и интегралов. В работах [3, 4] представлены результаты построения приближенных решений редуцированного уравнения на основе специальной версии метода ускоренной сходимости. В этих же работах дано обоснование необходимости применения приближенных методов к построению решений — в противовес методу использования точного аналитического решения в эллиптических функциях.

Наш подход основан в целом на двухступенчатой редукции: функциональной редукции к краевой задаче для ОДУ с квадратичной нелинейностью (первая ступень) и редукция к конечномерному алгебраическому уравнению (вторая ступень) — через нелинейную аппроксимацию Галеркина – Ритца по схеме Ляпунова – Шмидта.

Общая структура представленной в статье теоретической базы вычислительного алгоритма сохраняется при переходе к объемному диффузору и диффузору-улитке. В доработке нуждаются лишь отдельные блоки алгоритма, что вызвано наличием аналитических препятствий, связанных с усложнением редуцирующих переходов.

Обратимся к двумерному уравнению Навье – Стокса [5]

v + — v = vA(v) — grad (p).

d|X — матрица Якоби вектора скорости v =

Здесь A =   +   — двумерный лапласиан,

∂x ₁     ∂x ₂

v(x1,x2,t) по компонентам точки x = (x1,x2), p = p(x1,x2,t) — давление. Искомое поле векторов скорости v считается заданным на некоторой ограниченной области Q С R2 с гладкой границей и «стандартными» краевыми условиями.

В полярных координатах стационарное уравнение Навье-Стокса принимает следующий вид (см. [5]):

(U • v)u - v- = -|p +(Au - r2dlvv - ru), (U -V)v + = = — ig + (Av + Дdu — Г2), где

(U •V)

d   v d

∂r r ∂ϕ,

- d ²     1 d

= dr ^{2 +} rdr ⁺

1 d 2 r ² ∂ϕ ^{2 .}

К уравнениям Навье – Стокса добавляется

уравнение неразрывности

∂u u + ∂r r

1 dv о r ∂ϕ .

В преобразованиях, упрощающих уравнение (1), используются следующие соотношения (устанавливаемые непосредственной проверкой):

∂v rot — ∂x

= grad (A0);

∂v rot v

∂x

= [0, A(0)].

Здесь rot (v) := ddv i — d^ , 0(x i , X 2 , t) — так называемая вихревая функция, [0, у] — якобиан функций ψ, ϕ .

Условие неразрывности div(v) = 0 для двумерной жидкости в односвязной области приводит к тому, что решение обязано принимать следующий вид:

v ^:==^gr^ad(⁰⁾=(- д⁰ ;■.

Для функции ψ естественно потребовать выполнение граничного условия

(n, sgrad (0))

= 0,

∂ Ω

n — поле нормалей к границе области.

Пусть u : = rot(v) = A(0), и u = rot(v) = A(0). Применив двумерный ротор к левой и правой частям уравнения (1), получим уравнение Гельмгольца ([5], стр. 406)

A(0) = [A(0), 0] + v A ² (0).

3.    Подстановка Гамеля и редукция к ОДУ

Анализ стационарного варианта

[A(0), 0] + v A ² (0) = 0

уравнения Гельмгольца (4) можно осуществить, используя редуцирующй переход к краевой задаче для ОДУ ([5], с. 450 – 484). Наиболее известной редукцией является подстановка Гамеля, осуществляемая посредством сужения стационарного уравнения Гельмгольца на класс функций вида (см. [5], с. 478) 0 = Qq(9). Ниже Q := 0 rudd — поток жидкости через диффузорную дугу окружности {0 <  9 < 0, r = const} , в — величина раствора диффузорного угла.

Используя соотношения

A(y) = Qq 2 ,    [A(y), у] = -Q^:

, 2 2 q ’ q _r 4    ^,

д ² ( = 6 q‘ ∂r²r²r^{4 ,}

1-r ∂r r ²

2 q r ^{4 ,}

4 (Я rr

‘‘ = q ’’’’ r 4

получим (после подстановки Гамеля) вместо (5) следующее ОДУ:

q ’’’’ + 4 q ‘ + 2R q ’ q = 0 ,

где R = QQ — число Рейнольдса.

В случае плоского диффузора уравнение (6) дополняется краевыми условиями (см. (3))

q(0)=0 ,    q(e) = 1,    q ‘ (0)= q ‘ (e) = 0.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

ββ

Условие q(e) = 1 вытекает из того, что / q ' d9 = qQ J rud9 = 1 — (нормированный) поток 00 через сечение диффузора окружностью r = const (см. [3, 4]).

После масштабирующего преобразования угловой переменной 9 —» в9 получим краевую задачу q'''' + Xq" + 2R q'q = 0,(7)

q(0)=0, q(1) = 1, q'(0)= q' (1) = 0,(8)

где X = 4в ^{- 2} ,     TR = в¹^-

Замечание 1. Нетрудно установить, что краевая задача (7) – (8) является вариационной: левая часть уравнения (7) является градиентом функционала

V = /1 L(q'', q') d9,     L(q", q) =       - X(^- + TR q ‘ 3.(9)

J 0

Таким образом, решения уравнения (7) являются экстремалями функционала (9) (при условии (8)). Следовательно, построение решений уравнения (7) можно осуществлять на основе локальной и нелокальной версий вариационного метода Ляпунова – Шмидта.

Замечание 2. В работах [3, 4] представлены результаты построения приближенных решений уравнения (7) на основе специальной версии метода ускоренной сходимости. В этих же работах дано обоснование необходимости применения приближенных методов к построению решений уравнения (7) — в противовес методу использования точного аналитического решения в эллиптических функциях. Такая возможность имеется вследствие интегрируемости уравнения (7). Представление решений через эллиптические функции не удовлетворяет современным требованиям к приближениям вследствие недостаточной точности (10 - ⁴ — 10 ^{- 6} ) существующих таблиц значений эллиптических функций и интегралов. Требуемая точность в современных прикладных задачах — 10 ^{- 8} — 10 ^{- 10} и выше.

После первичного интегрирования уравнения (7) и замены q' = и получим краевую задачу и" + Xu + TR u- = c, c — const

(уравнение Джеффри – Гамеля),

u(0) = u(1) = 0

при дополнительном интегральном ограничении j ud9 = 1 -

Левая часть уравнения (10) является градиентом функционала действия

V := Z1 1 f((u')2 — Xu-) + 1 u3) J o 2 \ dθ

при краевых условиях (11). Функционал (13) удобно рассматривать (см. [7]) на гильбертовом пространстве H ¹ [0,1], состоящем из абсолютно непрерывных функций, удовлетворяющих условию (11) и имеющих производную класса L 2 [0,1]. Скалярное произведение в H 1 [0,1]

задается соотношением (u,v') ₁ = J u'v ' d9 .

Интегрирование (вторичное) уравнения (10) приводит к следующему интегральному соотношению (с двумя константами c, d):

2 ((u ‘ ) 2 +1. 2 ) + RRu ³

cu = d,

или 1 (u ' ) 2 + ^R (u + a) ³ — cu = d , где a =    , c = c + ^2 , d = d --^ 3-.

^{2          3                        ,}                2 R ^,            4 R ^,             24 R ²

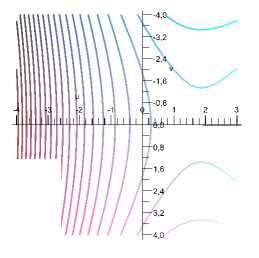
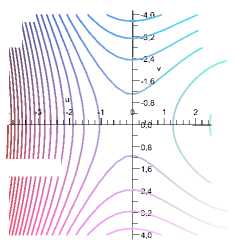
Изменение значений параметров приводит к изменению графика (рис. 1) и интегральных кривых (рис. 2), вплоть до слияния (на фазовом портрете рис. 2) локального минимума с седлом и их исчезновения (после перехода вектора параметров λ, R, c через каустику функ- ции 2 (v2 + Au2) + Ru3 — cu).

Рис. 1 . График функции, равной левой части интегрального соотношения (14)

-0.8

-0,8

-1.6

2,4/

-3.2

-4,0

-0.8

■0.8

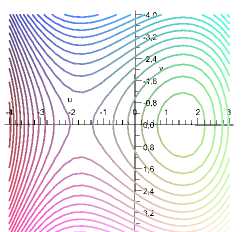
Рис. 2 . Интегральные кривые уравнения (10) при различных значениях параметров (14)

«Управляя» параметрами λ, R , c, d , можно получить изображения всевозможных геометрических форм интегральных кривых и их расположений относительно системы координат u, v (v := u') на фазовой плоскости. Рассматривая пересечения интегральными кривыми прямой u = 0, можно получить представление о тех фрагментах интегральных кривых, которые дают решение краевой задачи (10) – (11). Приближенные аналитические формулы для этих фрагментов можно получить, применив специальные вычислительные методы (например, методы, использованные в [3, 4, 7, 15]).

По-видимому, аналогичный подход можно применять при изучении других гидродинамических моделей, например, рассмотренных в [8–10].

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

4.    Случай нулевого значения числа Рейнольдса

Рассмотрим задачу (10) - (11) при R = 0 :

u " + Au = c, u(0) = u(1) = 0, j ud9 = 1.

Решения задачи (15) являются критическими точками квадратичного функционала jO 2 ((u‘)2 - Au2) d9

на гиперплоскости

M = {u _G H 1 [0,1] : j0 ud9 = 1} в тройке E = F = H = H ¹ [0,1] (см. [7]).

Теорема 1. Совокупность экстремалей сужения функционала (16) на гиперплоскость (17) есть объединение следующих серий векторов (при соответствующих значениях параметра λ):

s o ,k = “2k sin(nk9),    A = A o ,k :=(nk) ² ;

(S o )

(S e )

(SC e )

(C o ) (C e )

s _e,k = a(E) a _e (9), a _e (9) := sin(E + (n k - 2 e ) 9 ) - sin(e), A = A _e ,k := (n k - 2 e ) ² ; k = 2m - 1, m = 1, 2, ... , a(E) — величина, обратная к среднему значению функции a _e (9);

S e, 2 m = sin^) (sin(2n m 9 - e ) + sin(s)) =

—■ (cos(e) sin(2nm0) + sin(e)(1 — cos(2nm0))), m = 1, 2, ... , sm(e)

A = A _e , 2 m := (2nm) 2 ,     m = 1, 2, ... ;

f o ,j = 1 ^{- cos(2 jn9)}, ^A = ^ 0 ,3 ^:=^{(2 jn) 2} ;

f e,j = Ь ( е ) P eW ,     P e (9) = cos( e + 2(jn - e ) 9 ) - cos( e ) ,

^A = ^ e,j ^:=4^(jn - ^{e ) 2} , ^j = 1, 2,... ;

b(e) — величина, обратная к среднему значению функции p _e (0).

Доказательство проводится на основе общей формулы решений линейного неоднородного уравнения (15) с последующим подбором констант, соответствующих второму и третьему соотношениям в (15).

5.    Случай конечного значения числа Рейнольдса

При малых значениях числа Рейнольдса экстремали функцинала (13), суженного на гиперплоскость (17), можно вычислять как ветви экстремалей, зависящих от числа Рейнольдса, — посредством теории возмущений, основанной на непосредственном применении теоремы о неявной функции. При «конечных» значениях числа Рейнольдса возникает необходимость применения более мощных средств нелинейного анализа [11], например, применения нелинейного метода Галеркина – Ритца по схеме Ляпунова – Шмидта.

Возможность нелокальной конечномерной редукции в краевой задаче (10) – (11) поясним сначала на простейшем примере: правая часть уравнения x = e(x — x ² + x = 1) является сжимающим отображением [—2, 2] —> [—2, 2] при достаточно малых значениях параметра е). Зарождение свойства сжатия для отображения x —> e(x — x ² + 1) отражено в следующих графиках.

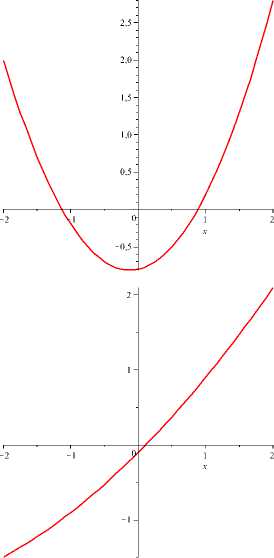
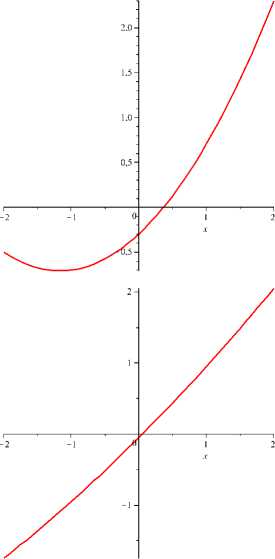
Рис. 3 . Графики функции f ( x ) = x — е ( х — x ² + 1) при Е = 0 , 8 , 0 , 3 , 0 , 1 , 0 , 05

Аналогичный эффект сжимаемости имеет место и в случае общего операторного уравнения x = B(g(x,x) + Cx + c),   x G F                           (18)

в банаховом пространстве F , если норма ||B^ f достаточно мала. Здесь g(x,x) — непрерывный квадратичный оператор F —> F , B , C — линейные непрерывные операторы F —> F , c G F .

Свойство сжимаемости оператора K (x) := B(g(x,x) + Cx + c) позволяет разыскивать приближенные решения уравнения (18) посредством стандартных итераций x n = K (x n - i ) [11].

Для осуществления нелокальной редукции Ляпунова-Шмидта в краевой задаче (10) – (11) запишем ее в виде операторного уравнения

f(w) := Aw — Aw + g(w,w) + c = 0, w G E,(19)

где E = C ² [0,1] П {w(0) = w(1) = 0}, A = —d²/d6² , g(w,w) := TRw ² , c — const. Оператор f действует из E в F = C [0,1]. Линейный оператор A является положительным и диагонализуемым:

k=1

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ek = nk2 sin(nk0) — собственная функция оператора A, отвечающая собственному значению (nk)2. Заметим, что собственные функции ek образуют ортонормированную систему в H 1[0,1].

Перепишем уравнение (19) в виде w — A-1(g(w,w) + Aw — c), w E H1 [0,1].                      (21)

Используя процедуру ортогонального разложения пространства в сумму подпространств, разобьем уравнение (21) в систему двух уравнений u -A-1 (g1 (w,w)) + Au — a) = 0, v — A- 1(g2(w, w)) + Av — b) = 0,

где A i := A| N , A 2 := A| N _{± n} E , N := Lin(e i ,..., e n ), w = u + v, u = ^f ^ k e k , v = k =1

E ^ k e k , a = E a k e k , b = E a k e k , a k = (c,e k h. Второе уравнение системы (22) k = n +1              k =1              k = n +1

рассмотрим в пространстве функций N^ П H1 [0,1]. Из спектральных свойств опратора A (см. (20)) вытекает, что при достаточно больших размерностях редукции n норма оператора A2 ■1 : N± П H1 —> N^ ПH1 становится малой, и поэтому оператор K(v) := A- 1(g2(u + v,u + v) + Av — b) переводит некоторый шар ||v^hi < L (в N^ П H 1) в себя, являясь при этом сжимающим. То есть мы оказываемся в условиях второго замечания. Это означает, что решения второго уравнения системы (22) можно получать в аналитической форме v = Ф(u),                                         (23)

с любой наперед заданной точностью, посредством итераций v _n = K (v _{n - 1} ). Подставив выражение (23) в первое уравнение системы (22), получим так называемое ключевое уравнение

т (u) := f 1 (u + Ф(u)) = 0                                 (24)

на конечномерном пространстве N . Все аналитические и топологические свойства исходного уравнения и его решений наследуются ключевым уравнением и его решениями [7]. Связь между решениями исходного и ключевого уравнений осуществляется формулой w = u + Ф(u).

Уравнение (24) является потенциальным с потенциалом (ключевой функцией)

W (u) := V(u + Ф(u)), u E N.

Поиск и анализ экстремалей функционала V можно осуществлять посредством изучения экстремалей ключевой функции W . Вычисление функции W и анализ ее критических точек можно осуществлять по технологиям, изложенным в [7, 11–15].

Заключительный этап предложенной здесь вычислительной схемы состоит в отборе тех решений задачи (10) – (11), для которых выполняется ограничение (12).

6.    Области редуцируемости модельного уравнения

Посредством оценок размера образа отображения K и его константы Липшица можно точно указать область, на которой допускается конечномерная редукция уравнения w = K(w).

Предварительно заметим, что имеют место следующие неравенства:

IIwIIf < Ilwll1   Vw G H1 ,     hA2 1(v)Hi <  2/^  n2 Ilvll1  Vv G N± n H1

n (n + 1)

(см. (20)). Следовательно,

|g(w.w)|i =2\     (ww')2 d9 < 2|w|f |w|i < 2 ||w||1.(26)

Пусть w G T l = {w G H ¹ [0,1] : |w| i < L}. Из оценки (26) получаем

IIK(v) 11l = IIA- 1(Av + g2(w-w) - b|1 < n2(n + 1)2 (A L + 2 L2 + в) ’ где в = |b|1. Следовательно, если ||K(v)11 < L, то оператор K переводит шар Tl в себя.

Последнее утверждение справедливо в случае выполнения соотношения (см. (27))

—    2 (AL + 2L2 + в) < L n2(n + 1)2

или

L 2 - pL + q < 0 ,                               (28)

где p = ⁿ ( n +2¹) —- , q = ^e . Для обеспечения свойства сжимаемости оператора K : T l —>

T L обратимся к оценке нормы разности значений K в произвольной паре точек v 1 , v 2 :

||K(V 2 ) - K (V 1 )1 1 = IA 2 ¹ (A(v 2 - V 1 ) + R ((u + V 2 ) ² - (u + V 1 ) ² )) 111 <

< _n 2 (n ₊ 1) 2 ^{(A + 4L) I} v ² - v ^{1 1 1} "

Получаем то, что для обеспечения свойства сжимаемости K достаточно потребовать выполнения условия

Y :=     \n2(A + 4L) < 1,                         (29)

n ² (n + 1) 2

или, что одно и тоже, условия A + 4L < n ² (n + 1) 2 .                                (30)

Таким образом, установлено следующее утверждение:

Теорема 2. При выполнении условий (28), (30) и при |u| 1 <  L оператор K (v) := A - 1 (R(u + v) ² + Av - b) переводит шар T l = {v G H ¹ [0,1] : |v| 1 < L} в себя и является сжимающим отображением Tl —> T l .

Замечание 3. Константа γ (см. (29)) позволяет оценивать скорость сходимости итераций v m +1 (u) = K (v m (u)) к редуцирующему отображению Ф(и):

D

RL + в D =. п ² (п + 1) 2

|v m (u) - Ф(и)| 1 < Y m _Г-^,

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

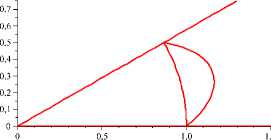
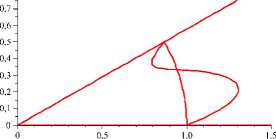
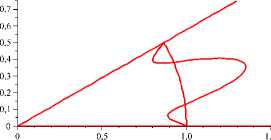
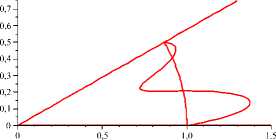
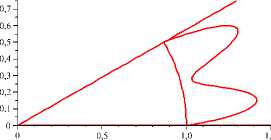
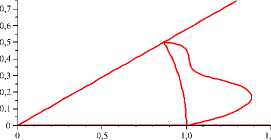
Рис. 4 . Эпюры скоростей для течений, близких к n -модовым, n ≤ 5

7.    Примеры эпюр скоростей стационарных течений, соответствующих экстремалям функционала действия

Ниже приведены примеры приближенно вычисленных эпюр скоростей на окружности r = 1 для течений, близких к n-модовым, n < 5 (рис. 4).

Замечание 4. Вслед за вычислением поля скоростей можно вычислить давление непосредственно на основе (2) (уравнения Навье – Стокса в полярных координатах).