Моделирование динамических режимов теплопровода системы теплоснабжения

Введение. Важнейшим фактором повышения энергетической эффективности теплоснабжения зданий является качество работы гидротранспортных комплексов, которая сопровождается различного рода переходными процесса- ми, характеризующимися значительными изменениями давления, расхода, гидравлической мощности, скорости движения жидкости и т.д. [1, 2]. Гидротранспортные комплексы представляют собой сложную энергоемкую систему, включающую насосные агрегаты с различными схемами соединения, гидродинамическую сеть, характеризующуюся наличием противодавления, нелинейностей, обусловленных местными сопротивлениями (задвижками, вентилями, обратными клапанами, разветвлениями трубопровода и т.п.), различными свойствами перемещаемой среды [3, 4].

За характеристику современной арматуры принята пропускная способность (терморегуляторы, регуляторы расхода теплоносителя, балансировочные клапаны и др.) в зависимости от объемного расхода воды при перепаде давления 105 Па. Изменение коэффициента перепускного клапана ведет к изменению таких параметров, как перепад давления и расход теплоносителя через клапан. Все это существенно снижает стабильность температурного режима гидротранспортной системы [5, 6]. Одним из способов снижения динамических процессов служит стабилизация температурного режима трубопроводной системы теплоснабжения, которая уменьшает перепады давлений и температуры теплоносителя [7, 8].

Существенную долю в исследовании динамических режимов тепловой сети занимает математическое моделирование. Известно несколько методов математического моделирования таких динамических режимов. Моделирование на анализе структуры трансцендентных передаточных функций позволяет исследовать динамику теплового состояния трубопроводной системы теплоснабжения, изменяющейся по длине элемента температурой греющего агента [9, 10].

Цель исследований. Определить влияние скорости течения теплоносителя на температуру в теплопроводе при скачкообразном и ступенчатом изменении скорости потока.

Методы и результаты исследований. На рисунке 1 приведена расчетная схема теплового баланса теплопровода при скачкообразном и ступенчатом изменении скорости потока.

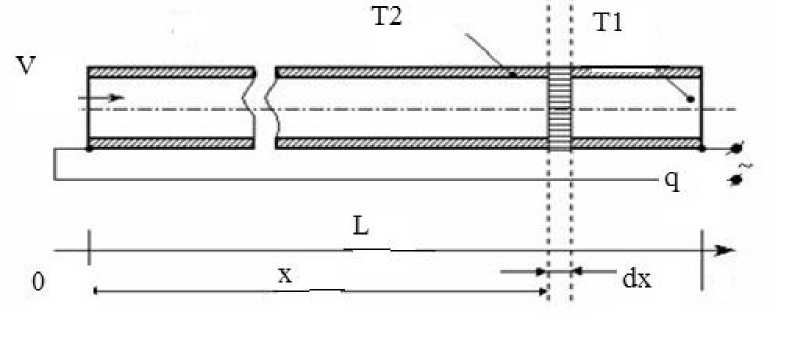
Рис. 1. Расчетная схема теплового баланса теплопровода при скачкообразном и ступенчатом изменении скорости потока: x – текущая координата аппарата, м; L – длина аппарата, м; V – постоянная скорость, м/с; T1 – температура стенки трубы системы отопления, ˚С; T2 – тем- Вт пература теплоносителя, ˚С; q – удельный тепловой поток, .

м ²

Для моделирования процесса передачи тарного кольца стенки трубопровода за время dt температуры в теплопроводе составлен диф- [8] ференциальный тепловой баланс для элемен-

(D2 - d2)

^ 2 / 2----- 4-----dx • dT₂ =

= ^ i ₂( ^ i — 22) ) • nd • dx • dt + a ₃₂ dD • dx • (T₃ — T₂ ) • dt,                 (1)

где с с – удельная теплоемкость жидкости, кДж                       кг

; γ2 – плотность теплоносителя, ; D – кгК 2                            м 3

наружный диаметр трубы, м; d – внутренний диаметр трубы, м; аг2 - коэффициент теплопе-

^ + <9^ 1 = J-(T₂

dt дх Т12 v 2

— T i ) ;

J t = ^^(Ti^-^ ^{+ k-} q ;

Вт редачи теплоносителя трубе,      ; t – текущее м2К время, с.

Тепловой баланс описывается дифференциальными уравнениями в частных производных (2), (3) с краевыми и начальными условиями [7].

T i ( х ,0) = T 2 ( х ,0) = 0; T i (0,t) = f i ( t); 21 --к - qt t) = ^ з ( t).

Здесь А(0,Л( t) и ^t t) - произвольные функции времени.

Решение системы (2)–(4) выполнено относительно температуры T1 потока жидкости. При этом температура теплоносителя – величина, не зависящая от координаты x и изменяющаяся только во времени. Получаем решение системы

или (x'p )=^ [1- ехр (—г Э+^ г ех» Нт ^       (5) T ^'P^^ + ^i-ад)-ехр(— Гад),          <6> где ρ – независимая переменная; x – текущая длина теплопровода.

Передаточная функция звена теплопровода

определяется следующим образом: W 1 =1/M(p).

(р)

ИД = ехр ( -  •      ■).

^{2       н} \ 19 N (р)7

Проведя деление M(p)/N(p ) , получим

“Р + --         (9)

()

Таким образом, функция звена теплопровода определится по формуле

W₂ = ехр

У х \ f X 1 \ \х

(  у)-^.  .•

где ехр(- ^ р) - чистое запаздывание, ехр (- ^ • ^) - постоянный коэффициент.

±3 1,      (10)

Т₂ I т₂ 3 )

а

При моделировании были взяты следующие значения: постоянные времени – T 12 =T 21 =T 23 =1 и время запаздывания - т_О = - ^ = 1 с.

При этом выражение (6) примет вид

С-    ... Д 8..1 ■ h (р)-

Ср)

(2,62 р +1)(О , 3 8р+1)

■ ] x ^0,368 • ехр(-р) • ехр Q^0- ⁽¹¹⁾

Таким образом, получим звено теплопровода с трансцендентной передаточной функцией

( 0 ,5                    О,5     ,      О, 5      .      О, 5

р (------) = 1 + 7-------Г + 7-------77 + 7------77 + ‘' ‘

,                             ( ,          )       ( ,         )         ( ,          )

Каждый член уравнения (12) представляет собой апериодическое звено n-го порядка, поэтому погрешность определится

Д< ехр(Ю-(1+ £ + ^ + ^+-) . (13)

На рисунке 2 представлена схема моделирования системы по изменению скорости потока скорости потока в Matlab–Simulink.

Результаты моделирования по изменению скорости потока теплоносителя приведены на рисунке 3.

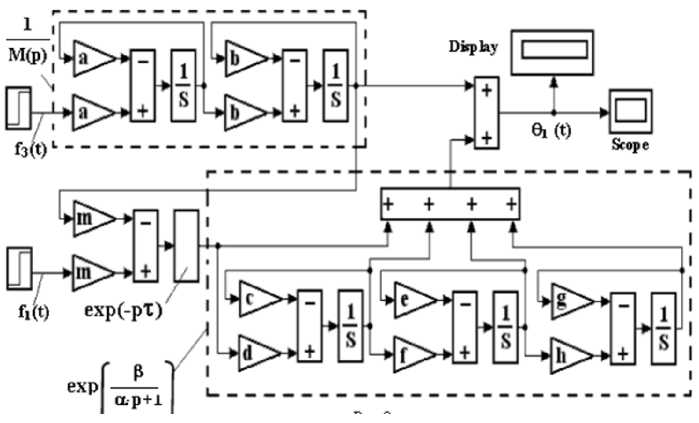
Рис. 2. Схема моделирования по изменению скорости потока: 1 - блок-схема уравнения (2); 2 - блок-схема уравнения (3)

Результаты моделирования показали, что при изменении скорости потока на 1,0 м/с температура в теплопроводе повышается на 0,5ºС. При изменении скорости потока на 0,5 м/с температура в теплопроводе уменьшается, что может вызвать недогрев теплоносителя. В целом недогрев теплоносителя за счет увеличения скорости потока компенсируется увеличением коэффициента теплоотдачи.

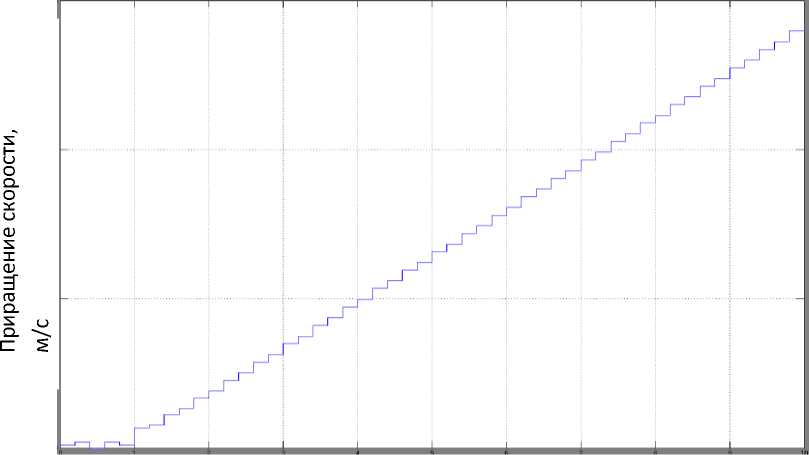
1,0     2,0     3,0     4,0     5,0     6,0     7,0     8,0 Время, с

Рис. 3. Изменение скорости потока на 0,1м/с

На рисунке 4 приведены зависимости изменения температуры при скачкообразном возму-

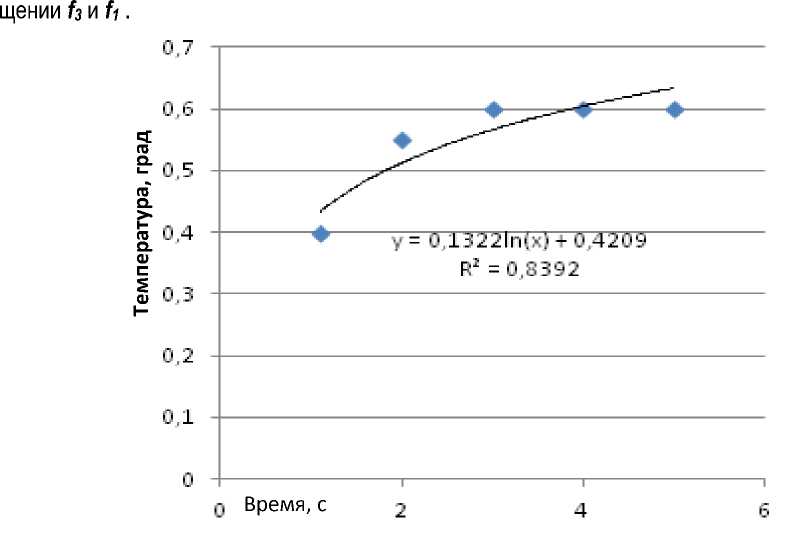
Рис. 4. Реакции системы (2)–(4) на единичные скачкообразные возмущения по функции f3 и f1

Заключение. Разработанная математическая модель теплопровода используется для выполнения процессов моделирования системы теплоснабжения в условиях переходных процессов и позволяет получить количественные характеристики параметров, влияющих на гидравлическую устойчивость в части влияния скорости потока на температурный режим системы теплоснабжения зданий.