Моделирование динамического поведения мостовидного зубного протеза с помощью метода конечных элементов

Исследования последних лет, основанные на данных Всемирной организации здравоохранения и отечественных авторов, свидетельствуют о высоком уровне распространенности частичного отсутствия зубов и динамике его роста [3, 5, 17–19, 25, 27, 39, 43]. Основной причиной потери зубов являются кариес и его осложнения. Но замещение дефектов протезами ведет к деформации зубных рядов, нарушению их окклюзионных взаимоотношений, перепрограммированию функций мышц и височно- © Крупнин А.Е., Харах Я.Н., Киракосян Л.Г, Арутюнов С.Д., 2018 Крупнин Артур Евгеньевич, инженер-исследователь лаборатории полимерных материалов; ассистент кафедры прикладной механики, Москва

Харах Ясер Насерович, ассистент кафедры пропедевтики стоматологических заболеваний, Москва Киракосян Левон Гамлетович, старший лаборант кафедры пропедевтики стоматологических заболеваний, Москва

Арутюнов Сергей Дарчоевич, д.мед.н., профессор, заведующий кафедрой пропедевтики стоматологических заболеваний, Москва нижнечелюстного сустава, формированию трудноизлечимых, а порой неизлечимых заболеваний зубочелюстного аппарата.

В стоматологической практике несъемные зубные протезы являются самыми распространенными ортопедическими конструкциями для замещения включенных дефектов зубных рядов [13]. Однако при их использовании достаточно часто возникают поломки [33, 36], обусловленные врачебными ошибками прогнозирования результатов лечения из-за необоснованного выбора опорных зубов, конструкции протеза, технологии изготовления и конструкционного материала. Для снижения риска разрушения и прогнозирования влияния установленного протеза на твердые и мягкие ткани широко применяются численные методы, в частности, метод конечных элементов [6, 22, 23, 30, 35, 36, 38, 40, 46, 48].

Метод конечных элементов позволяет оценить максимальные нагрузки, которые выдерживает изделие, напряжения и деформации, возникающие в протезе и окружающих тканях. Такой подход дает возможность еще на стадии проектирования выбрать наилучший вариант конструктивного исполнения, соответствующий биомеханическим требованиям, сократив тем самым ресурсы и предотвратив возможные усложнения после имплантации.

Результат численного исследования напряженно-деформированного состояния конструкций зависит от многих аспектов. Важными шагами являются редукция исследуемого нативного объекта до адекватного модельного представления и интерпретация нагрузок, действующих на биомеханическую систему. В первом случае речь идет о выборе геометрии исследуемой области и представлении механических свойств материалов, из которых эта система состоит. Многие задачи биомеханики зубочелюстного аппарата успешно решаются в двумерной (плоской) постановке [8–10, 21, 22, 32, 35, 38, 40].

Несмотря на определенные допущения и ограничения, накладываемые сведением трехмерных систем к двумерным, решение плоских задач имеет ряд преимуществ [30]: качественная густая сетка, уменьшение времени решения задачи, возможность получения быстрых результатов на нескольких моделях. Это особенно ценно в задачах, где требуется оценить влияние одного или нескольких параметров на другие или на отклик системы в целом. Выбор двумерной схемы хорошо согласуется с экспериментальными результатами [22], а полученные решения плоских задач соответствуют решениям, аналогичным трехмерным в исследуемом сечении. Решение задач в трехмерной постановке дает более полную картину деформирования системы, но априори имеет большую размерность и требует значительных вычислительных мощностей для получения адекватного интерпретируемого результата [30].

Сложившаяся на данный момент культура и методология решения задач биомеханики зубочелюстного аппарата с использованием численных методов позволяет говорить о применимости линейно-упругих моделей мягких (пульпа, периодонт) и твердых (эмаль, дентин, кортикальная, альвеолярная и губчатая кости) тканей. При численной оценке прочности протезов доминирует использование статического анализа, применяющегося в случаях не зависящей от времени, медленно меняющейся нагрузки, действующей на биомеханическую систему [30, 32, 35, 40]. Однако исследования показывают, что жевательные нагрузки, воспринимаемые конструкцией протеза и окружающими тканями, изменяются с течением времени [46], возбуждая в системе колебательные процессы, а отклик зависит не только от значения действующей силы, но и от демпфирующих характеристик [16]. Актуальной становится задача исследования напряженно-деформированного состояния мостовидного зубного протеза методом конечных элементов с учетом временной зависимости силы, сопоставление с результатами статического анализа. Расширение возможностей математического инструментария позволит оценить динамический отклик и напряженно-деформированное состояние системы, выявить закономерности, присущие исследуемым процессам и в дальнейшем сформулировать требования, предъявляемые к проектируемому изделию.

Несмотря на большое число работ, посвященных биомеханике зубочелюстной системы, очень малая часть из них посвящена исследованию динамических процессов. Так, в работе [45] на примере титанового дентального имплантата был численно проведен модальный анализ и показано, что характеристики динамического отклика системы зависят от времени действия импульса. В исследовании [16] численно изучался отклик системы, состоящей из резца верхней челюсти и окружающих тканей, при действии сосредоточенной силы, изменяющейся по синусоидальному закону в течение 8 мс. Показано, что демпфирующие свойства системы влияют на напряжения, возникающие в зубе, а максимальные динамические напряжения меньше статических напряжений. В то же время в работе [47] на примере титанового дентального имплантата показано, что динамические напряжения, возникающие в имплантате, выше статических. Определение собственных частот и форм колебаний сегментов верхней челюсти, а также зависимость собственных частот от модуля упругости периодонта и введения демпфирования подробно изложено в [24]. Подход к идентификации динамических нагрузок, действующих на мостовидные протезы двух исполнений при жевании, представлен в [46]. Влияние толщины окружающей зуб кости на резонансную частоту описан в [15]. Анализ отечественных и зарубежных работ обнаруживает недостаток освещения методов динамического анализа применительно к расчету мостовидных зубных протезов и дентальных протезов в целом. В то же время выстроенный аппарат теории механических колебаний [1, 4] позволяет предположить, что в мостовидных зубных протезах при определенных условиях нагружения могут возникать колебательные, близкие к резонансным, режимы. Игнорирование динамической природы сил, действующих на биомеханическую систему, может повлечь разрушение протеза раньше прогнозируемого срока. Следствием этого являются не только повторная операция, сопряженная с финансовыми затратами, но и травмы мягких тканей зуба, стресс и дискомфорт пациента.

В ряде работ при оценке напряженно-деформированного состояния зубных протезов и окружающих тканей влияние пульпы на распределение деформаций, напряжений и энергии не учитывается [6, 10, 24, 46, 48]. Несмотря на известные в медицине и биологии функции пульпы, ее механические функции остаются малоизученными. Например, в работе [14] утверждается, что пульпа играет роль естественного амортизатора зуба без приведения количественных оценок.

Настоящая работа является первым этапом на пути создания методологии проектирования и расчета зубных протезов, в которой устанавливается связь между результатами статического и динамического анализа, формулируются условия применимости каждого из видов анализа. Количественно характеризуется вклад пульпы в демпфирование вынужденных колебаний биомеханической системы. Задача решается в плоско-деформированной постановке на примере мостовидного зубного протеза, сделанного из полиметилметакрилата, широко использующегося в качестве материала для дентального протезирования благодаря хорошей биосовместимости и адгезии, отсутствию вкусовых свойств и нерастворимости в биологических жидкостях (кровь, слюна) [41]. На основании результатов экспериментального исследования керамического мостовидного зубного протеза схожей конструкции проводится верификация численной модели. Сопоставляются результаты статического и динамического анализа. Количественно характеризуется влияние пульпы на напряженно-деформированное состояние протеза и демпфирующие свойства биомеханической системы в целом.

Методы и материалы

Теоретические сведения

Разрешающее уравнение метода конечных элементов при решении статических задач имеет вид [2]

Ku = f ,

где K – матрица жесткости, u – вектор узловых перемещений, f – вектор узловых сил. Это классическое уравнение применяется при решении задач, когда силы, действующие на систему, не зависят от времени, т.е. постоянны, или являются медленно меняющимися функциями времени. Из теории колебаний [2, 4] известно, что при стремлении частоты возбуждающей силы к собственной частоте колебаний системы амплитуда колебаний увеличивается. Если сила действует в течение короткого интервала времени, сопоставимого с периодом свободных колебаний системы, то в системе могут возникать колебательные процессы. Уравнение движения системы с конечным числом n степеней свободы в векторно-матричной форме записи имеет вид [1, 46]

Mu ( t ) + BU ( t ) + Ku ( t ) = f ( t ) ,

• u (0 ) = u ", (2) ,u (0 ) = u °, где u (t), u (t), u (t) - векторы узловых перемещений, скоростей и ускорений, М, B и K - матрицы масс, диссипации и жесткостей соответственно, u (0) = u0, u (0) = u0 -векторы узловых перемещений и скоростей в начальный момент времени t = 0.

Установлено [16, 24], что демпфирование оказывает значительное влияние на динамическое поведение зубочелюстных систем. Если распределение сил трения в системе заведомо не известно, то общепринятым [1, 12, 24, 46] является использование модели Рэлея (пропорциональное демпфирование), компоненты в которой определяются следующим образом:

B = а М + P K . (3)

Коэффициенты а и в отвечают за демпфирование низкочастотных и высокочастотных форм соответственно. Для i -й формы колебаний параметры а и в связаны через безразмерный коэффициент демпфирования ^ следующим соотношением:

а вго

-         +,

2 го_г      2

где го - круговая собственная частота i -й формы колебаний в системе без учета демпфирования. Известно [16], что коэффициенты ^ в задачах биомеханики зубочелюстного аппарата могут принимать значения от 0,091 до 0,24. По итогам модального анализа определяются n собственных форм колебаний, суммарно задействующих более 90% общей массы системы. Для задания ^ используется методика, предложенная в работе [12]. Выражения для коэффициентов матрицы диссипации в модели Рэлея выражаются следующим образом:

nn   n a =

• 
  

nn e™2 e Л - nn

Z1  Z1 ю .

e=

nn   n

2 E^E±-nE^-

i = i ® .

i = i ю ,

n

n

E 2т - n² i = 1 ^ю .

Для энергетической оценки демпфирующих свойств системы введем параметр, равный отношению энергии, рассеиваемой за один период колебаний, к максимальной упругой энергии - коэффициент поглощения v [1]:

V =

W-U - v^ и ” v

В этом выражении U , U – значения потенциальной энергии упругой деформации для первого и второго периода колебаний соответственно. Коэффициент поглощения позволяет оценить, насколько существенно демпфирующие параметры системы влияют на процесс затухания колебаний.

Геометрия модели

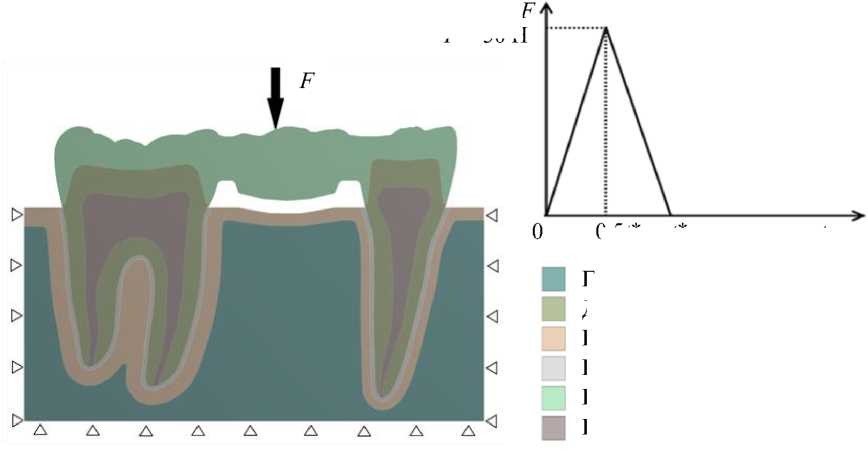
Объект исследования представлен мезиодистальным сечением участка нижней челюсти, зубного ряда и мостовидного протеза, включающего опорные искусственные коронки на первый премоляр и первый моляр, промежуточную часть – фасетку (недостающий второй премоляр), кортикальную и губчатую кости, периодонт и пульпу (рис. 1). Геометрия зубов получена по результатам компьютерной томографии с последующим воссозданием трехмерных моделей.

F = 50 H

0,5 t *

t , c

Губчатая кость Дентин Кортикальная кость Периодонт

Полиметилметакрилат Пульпа

Рис. 1. Геометрия модели, нагрузка и граничные условия

Высота в сечении премоляра составляет 21 мм (6,19 мм – коронка, 14,81 мм – корень), моляра – 20,38 мм (6,19 мм – коронка, 14,19 – корень). Длина мостовидного протеза – 31 мм, толщина шейки – 5,4 мм, радиусы скруглений шейки – 0,4 мм. Толщина периодонта равномерна по длине корня зуба и составляет 0,3 мм [28, 29]. Толщина кортикального слоя также постоянна по длине корня зуба и равна 1,5 мм для премоляра и 2 мм для моляра [11, 20, 37].

Нагрузки и граничные условия

Для решения задачи определения напряженно-деформированного состояния протеза в статической и динамической постановках к бугорку на окклюзионной поверхности фасетки приложена сосредоточенная сила [40, 46] F = 50 Н (см. рис. 1). При статическом расчете сила линейно возрастает от 0 до 50 Н. При решении динамической задачи сила линейно возрастает от 0 до 50 Н в течение времени t ^* /2, после чего линейно убывает со значения 50 Н до нуля за то же время t ^* /2. Так как длительность действия нагрузки t ^* на зубы и протез может измеряться сотыми [46], тысячными [16] и десятитысячными [45] долями секунды, исследовался отклик модели при t * = 2 - 10 " ⁵ с, t * = 2 - 10 " ⁴ с, t * = 2 - 10 " ³ с, t * = 2 - 10 - ² с, t * = 2 - 10 - ¹ с. На границы расчетной области наложены кинематические граничные условия [22, 42].

Задача экспериментальной верификации решалась в статической постановке, исходные данные приведены [48].

Конечно-элементная модель

Задача решалась в плоско-деформированной постановке [8–10, 21, 22, 32, 35, 38, 40]. Разбиение модели на конечные элементы и численное решение проводилось в программном пакете ANSYS . Для определения числа конечных элементов, в полной мере отражающих процесс распределения нагрузок в системе и динамический отклик при действии возбуждающей силы, проведен тест на сходимость значений эквивалентных (по Мизесу) напряжений от числа элементов [23]. После проведения теста на сходимость окончательное число 6-узловых [32] элементов PLANE 183 составило 63 289 (рис. 2).

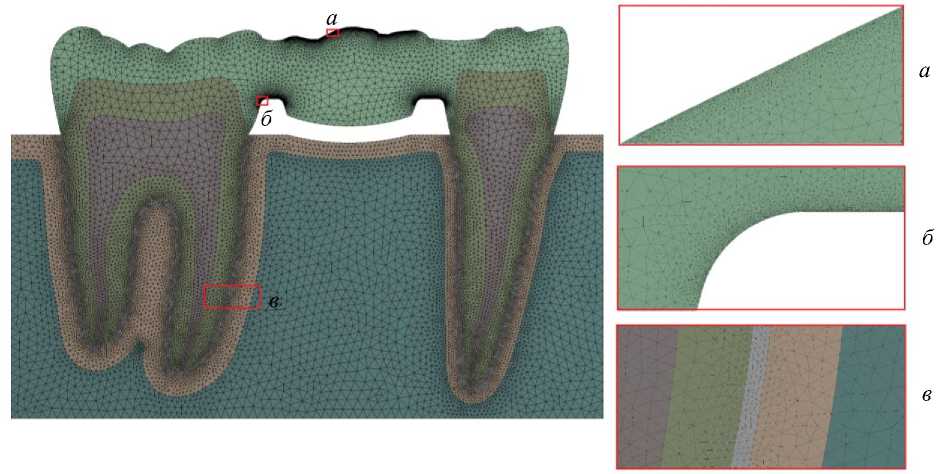
Рис. 2. Конечно-элементная модель ( а , б , в ‒ области сгущения сетки)

Размер элементов на окклюзионной поверхности и в областях скруглений шейки – 0,005 мм. Качество сетки контролировалось средними значениями параметров Element quality = 0,94, Skewness = 9,58∙10 ^–2 и Orthogonal quality = 0,94. Толщина слоя цемента между мостовидным протезом и поверхностями препарированных зубов считалась незначительной и в расчетах не учитывалась [6].

Материалы протезов, твердые и мягкие ткани нижней челюсти в процессе моделирования предполагались однородными, изотропными и линейно-упругими [47, 48]. Механические свойства материалов взяты из [7, 26, 34, 48] и представлены в таблице.

Механические свойства материалов

Материал	Модуль Юнга Е , МПа	Коэффициент Пуассона µ	Плотность ρ, кг/м 3
Кортикальная кость	12 200	0,26	1100
Губчатая кость	1220	0,31	270
Дентин	18 600	0,31	203
Пульпа	2	0,45	95
Периодонт	70	0,45	135
Полиметилметакрилат	3000	0,38	1190
Керамика	15 600	0,28

Результаты

Тест на сходимость решения

Результаты теста на сходимость решения представлены на рис. 3. Из графика видно, что выбранная конфигурация сетки обеспечивает незначительное расхождение в результатах (менее 1%) по сравнению с результатами, полученными на сетке с большей густотой.

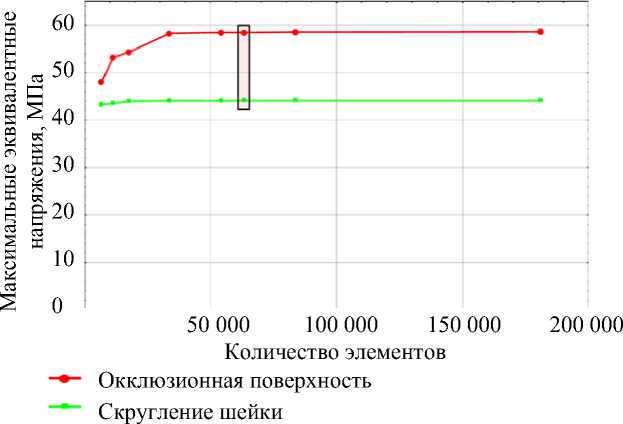
Рис. 3. Результаты теста на сходимость напряжений в локациях протеза от числа элементов сетки

Экспериментальная верификация

Результаты экспериментальной верификации представлены на рис. 4.

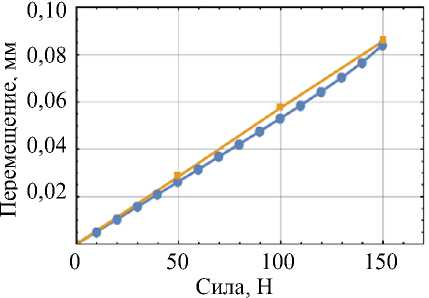
—•— 2 D

3 D

а

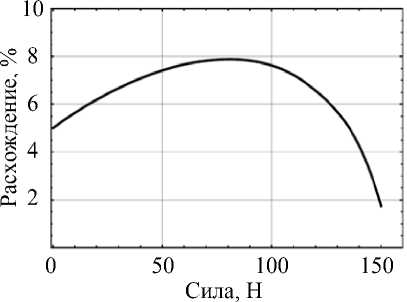
Рис. 4. Результаты экспериментальной верификации двухмерной модели: а – зависимость «перемещение – сила», воспроизведенная по результатам работы [48]; б – расхождение в результатах

Видно, что максимальное расхождение перемещений составляет менее 8%. Меньшие значения перемещений объясняются тем, что рассматриваемый протез имеет увеличенную толщину шейки (5,4 мм против 4,08 мм) по сравнению с аналогом из работы [48]. Таким образом, можно говорить о правомерности применения двумерной постановки для рассматриваемого класса задач.

Статический анализ

При решении задачи как в статической, так и в динамической постановке максимальные эквивалентные напряжения в протезе возникают на окклюзионной поверхности и в области скругления шейки ближе к моляру (рис. 5).

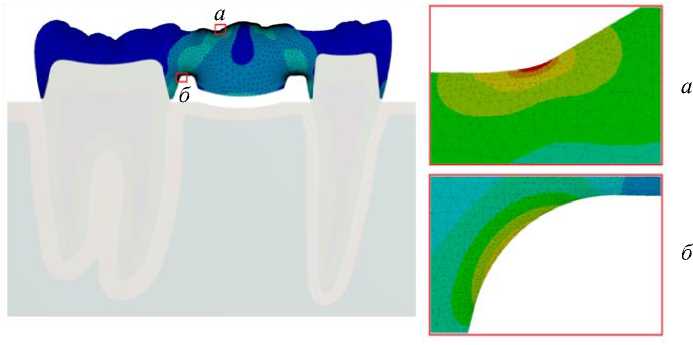
Рис. 5. Области максимальных эквивалентных напряжений в протезе, МПа

( а , б - области наибольших эквивалентных напряжений)

58,524 52,022 45,519 39,016 32,514 26,011 19,509 13,006

6,5034 0,0008

В модели с учетом пульпы максимальные эквивалентные напряжения на окклюзионной поверхности составили 58,5 МПа, в шейке – 44,1 МПа. В модели без учета пульпы – 58,6 и 44,2 МПа соответственно. Перемещения точки приложения силы в модели с учетом пульпы – 0,0943 мм, без учета пульпы – 0,0949 мм. Различие между величинами составляет менее 1%, что свидетельствует о применимости упрощенной модели (без учета пульпы) при выполнении статических расчетов в задачах проектирования зубных протезов.

Динамический анализ

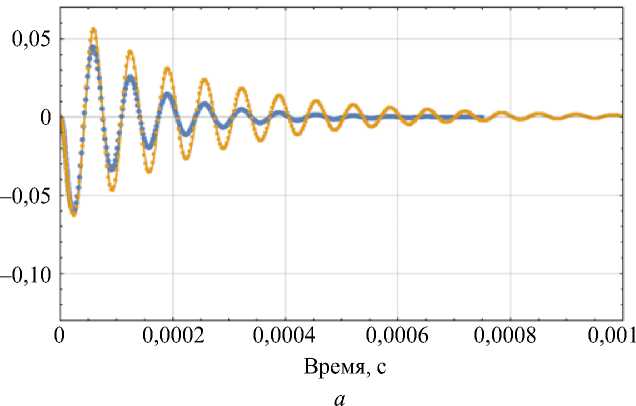
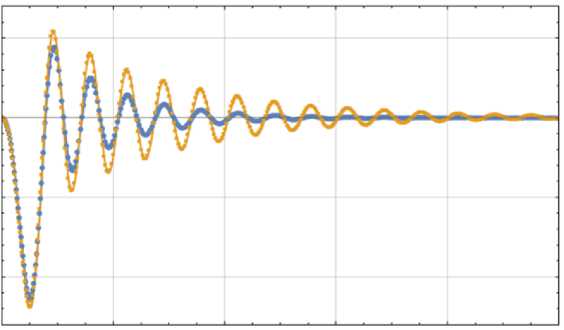
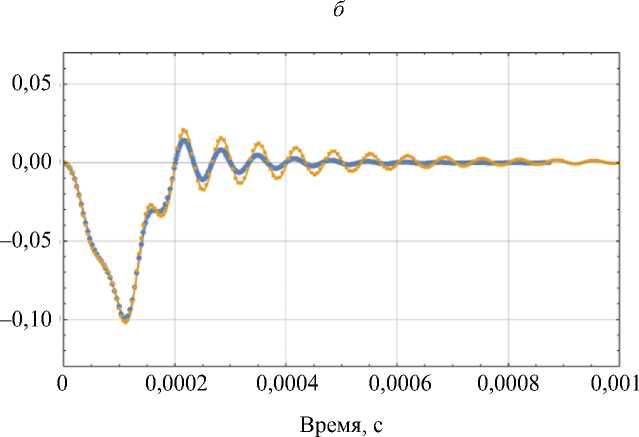
По результатам модального анализа установлено, что влияние демпфирования и учета пульпы на первую собственную частоту несущественно. Значение первой собственной частоты равно ν= 12 000 Гц. Таким образом, период свободных колебаний, соответствующий ν , равен T = 8,3 ⋅ 10 ^{- 5} c. Поэтому случай t ^* = 8,3 ⋅ 10 ^{- 5} с также был проанализирован. Для модели с пульпой число первых собственных форм колебаний, суммарно задействующих более 90% общей массы системы, равно 28. Для модели без учета пульпы – 23. Для модели с пульпой коэффициенты α = 4, 24 ⋅ 10 ^{- 4}, β = 1, 84 ⋅ 10 ^{- 6}, для модели без учета пульпы – α = 6,13 ⋅ 10 ^{- 2}, β = 9, 45 ⋅ 10 ^{- 7}. Графики перемещений точки приложения силы представлены на рис. 6 (здесь и далее: на всех графиках синий цвет соответствует модели с пульпой, оранжевый – без пульпы).

Из графиков видно, что ярко выраженный затухающий колебательный процесс имеет место при кратковременных воздействиях на систему. В случае t ^* ≥ 2 ⋅ 10 ^{- 3} с нагружение можно считать статическим, без возникновения в системе колебательных процессов, поэтому соответствующие графики не приводятся. Графики максимальных эквивалентных напряжений, возникающих на окклюзионной поверхности и в шейке, представлены на рис. 7 и 8 соответственно.

В модели с учетом пульпы перемещения и максимальные напряжения ниже, чем в модели без учета пульпы, а скорость затухания колебаний в первом случае значительно выше. Анализ зависимостей перемещений и напряжений позволяет сделать вывод о том, что пульпа обладает энергопоглощающей функцией и выступает природным демпфером в зубочелюстном аппарате. Амплитудные значения перемещений и напряжений для первого колебания (являющиеся максимальными) в моделях с учетом и без учета пульпы различаются не более чем на 3%. В случае, когда t ^* = 8, 3 ⋅ 10 ^{- 5} с, максимальные напряжения на окклюзионной поверхности достигают предела текучести (для полиметилметакрилата предел текучести при растяжении составляет 65 МПа). Именно в этой области будет происходить стирание материала. Важно отметить, что при t ^* = 8, 3 ⋅ 10 ^{- 5} с в системе начинают накапливаться пластические деформации, а на окклюзионной поверхности возникает чередование областей наибольших напряжений в зависимости от амплитудных положений фасетки зубного протеза. Этим обусловлен вид зависимости на рис. 7, б .

Коэффициент поглощения энергии

На рис. 9 показаны значения коэффициента поглощения в зависимости от длительности действия силы F . Из графика следует, что пульпа может поглощать до 30% накопленной за первый цикл колебаний энергии. Для случаев t ^* ≥ 2 ⋅ 10 ^{- 3} с предполагалось, что происходит полное рассеивание накопленной энергии, поэтому ψ= 1.

Перемещение, мм                     Перемещение, мм                     Перемещение, мм

0,05

–0,05

–0,10

0       0,0002    0,0004     0,0006    0,0008     0,001

Время, с

в

Перемещения точки приложения силы при: а - t * = 2 - 10 5 с; б - 1 * = 8,3 - 10 — ⁵ с; в - t * = 2 - 10 ^{- 4} с. Знак «минус» соответствует перемещению точки вниз

а

Время, с

в

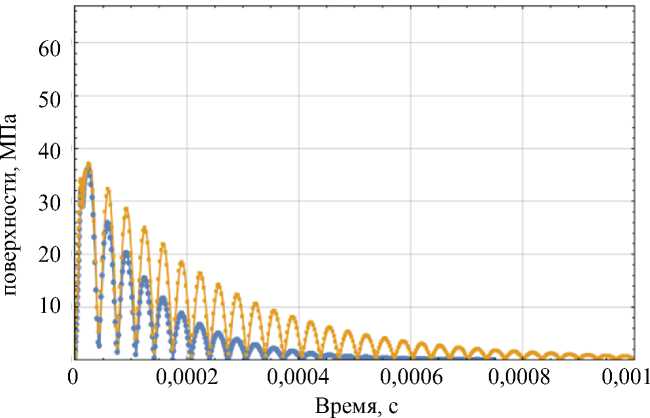
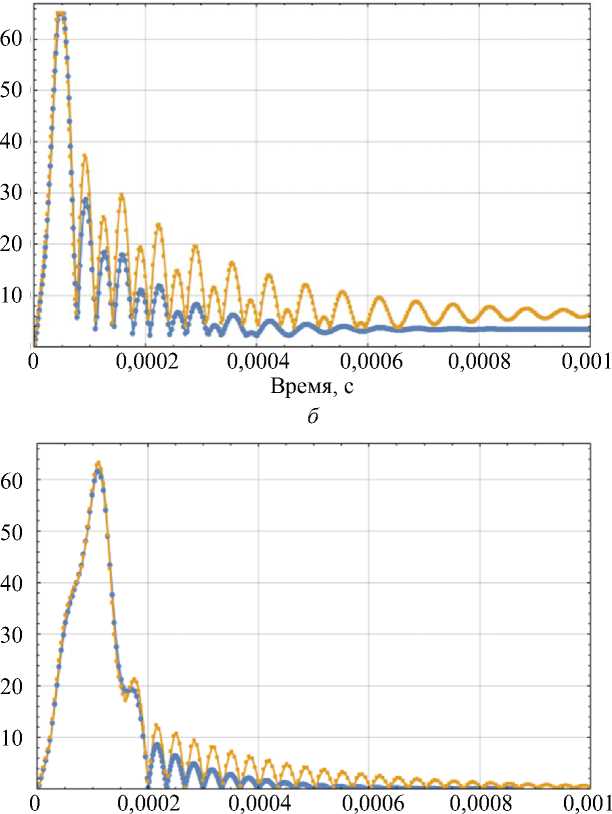
Рис. 7. Максимальные эквивалентные напряжения на окклюзионной поверхности

протеза при: а - t = 2 - 10 5 с; б - t = 8,3 - 10 5 с; в - t = 2 - 10 4 с

Время, с

в

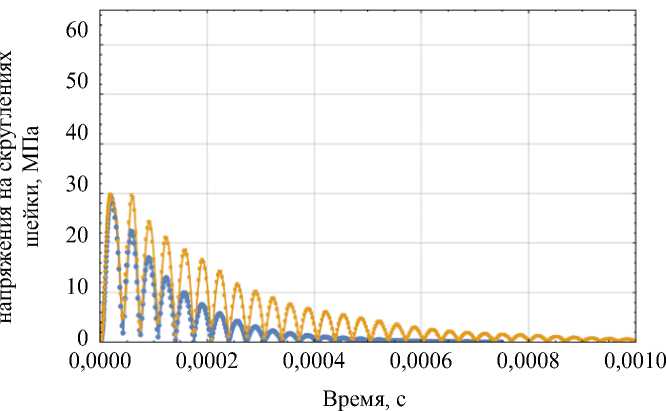
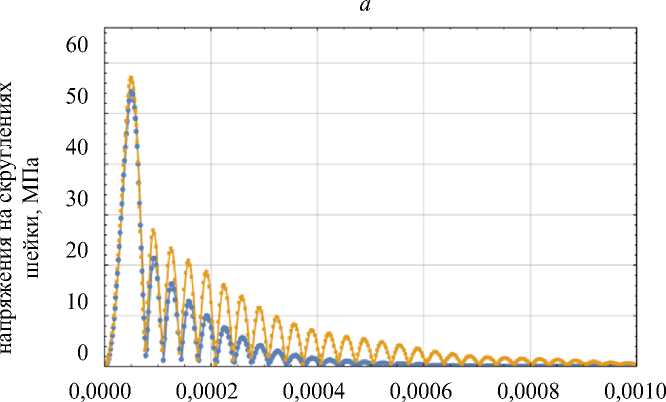
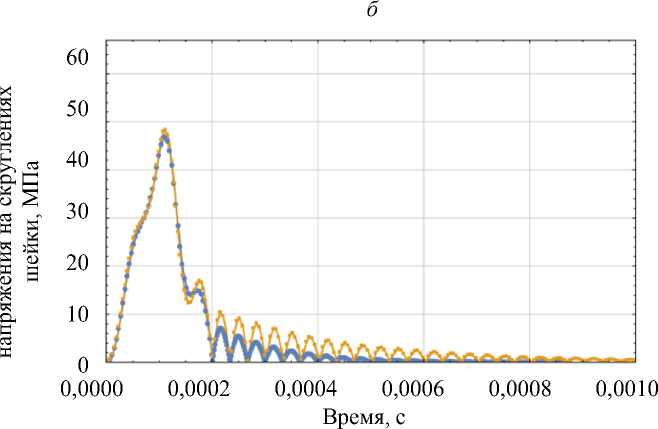
Рис. 8. Максимальные эквивалентные напряжения на скруглениях шейки протеза

при: а - t = 2 - 10 5 с; б - t = 8,3 - 10 ⁵ с; в - t = 2 - 10 4 с

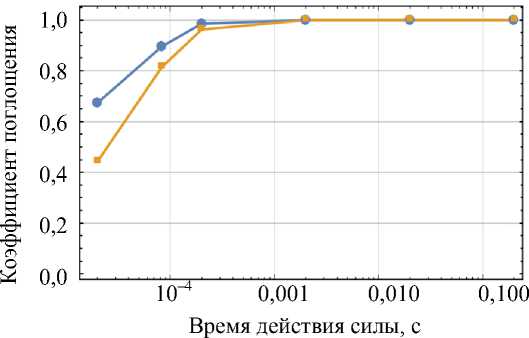
Рис. 9. Значения коэффициента поглощения энергии при разных режимах нагружения

Сравнение результатов статического и динамического анализа

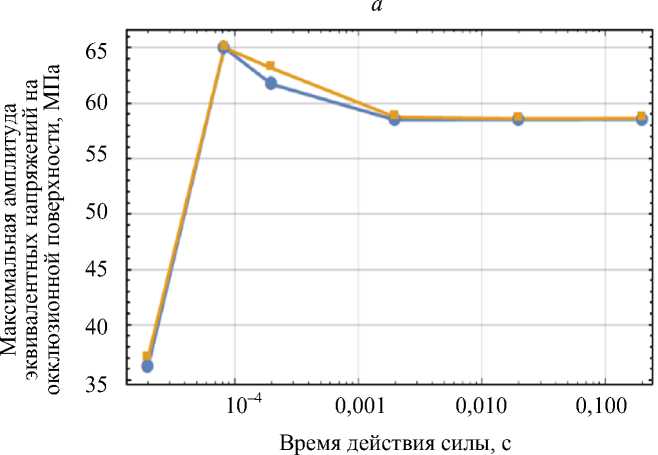
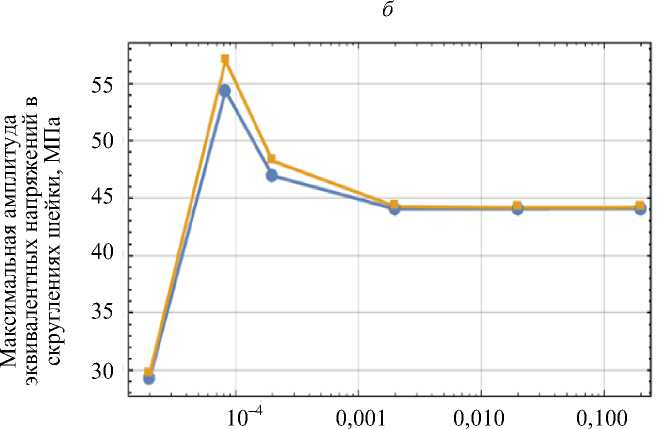
На рис. 10 представлены зависимости амплитудных значений перемещений и напряжений для исследуемых режимов нагружения в моделях с учетом и без учета пульпы.

В случаях, когда время действия силы t ^* ≥ 10 ^{- 3} c, динамические перемещения и напряжения стремятся к статическим. При значении t ^* = 10 ^{- 5} с динамические перемещения и напряжения значительно меньше статических. При стремлении длительности действия силы к периоду свободных колебаний, соответствующих первой собственной частоте, наблюдается возрастание амплитудных значений динамических перемещений до 0,12 мм, напряжений – до 65 и 55 МПа соответственно. Таким образом, динамические напряжения могут превышать статические на 11%, достигая предела текучести материала.

Выводы

При решении задач биомеханики зубочелюстного аппарата с применением численных методов очень важно грамотно интерпретировать условия, в которых функционирует протез in vivo . Это определяет методику, инструментарий решения сформулированной модельной задачи и, как следствие, результат. В работе показано, что использование динамического анализа при оценке напряженно-деформированного состояния мостовидного зубного протеза в случаях действия кратковременных сил помогает глубже понять природу и назначение отдельных звеньев биомеханической системы. Так, установлено, что пульпа играет роль естественного демпфера, гасителя вынужденных колебаний в системе, что позволяет избежать дислокации корней зубов, которые могут привести к травме периодонта. Кроме того, показано, что важным этапом при проектировании мостовидных зубных протезов и имплантатов в целом является проведение модального анализа с целью определения собственных частот и резонансных режимов. Изменяющиеся во времени жевательные нагрузки, действующие на зубной протез, могут привести биомеханическую систему в колебательное движение с амплитудными значениями напряжений, близкими и достигающими предела текучести. Таким образом, оценка напряженно-деформированного состояния протеза под действием статических сил может быть заниженной, так как такой подход не учитывает всего спектра физиологических нагрузок.

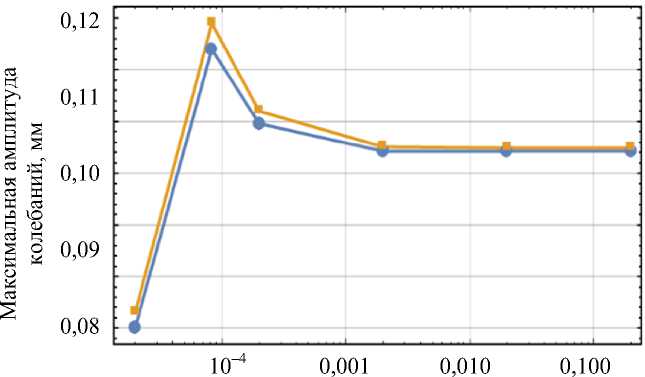
Время действия силы, с

Время действия силы, с в

Рис. 10. Максимальные амплитудные значения при разных режимах нагружения: а – перемещения; б – напряжения на окклюзионной поверхности; в – напряжения в скруглениях шейки